제 38회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 38회 전국 대학생 수학경시대회
제 2 분야
2019년 11월 9일 (10:00 - 13:00)
1. 다음 극한값을 구하여라.

Solution.

2. 다음 미분방정식의 해를 구하여라.

Solution.
우선 x(t)와 y(t)의 관계를 쉽게 구할 수 있다. (공식 풀이는 x(t)가 잘못 기술되어 있다.)

따라서 주어진 미분방정식의 해는 다음과 같다.
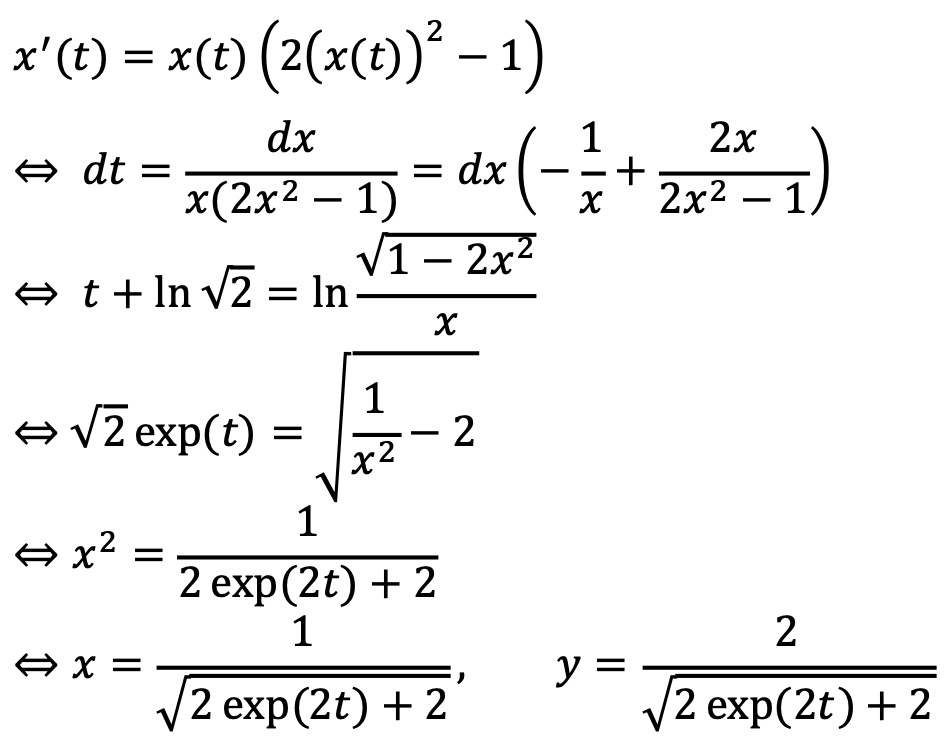
3. 영역 W = {(x, y, z) ∈ ℝ3 : x2 + y2 ≤ 1, |z| ≤ 1}에서 두 벡터장 F와 G가 다음과 같이 주어져 있다.
F(x, y, z) = (sin xy, sin yz, 0), G(x, y, z) = (exp(x2 + y2 + z2), cos xz, 0)
다음 적분값을 구하여라. (단, curl(F) = ∇ × F이다.)

Solution.

∫∫∫ -y cos yz exp(x2 + y2 + z2) dV = 0이다. 왜냐하면, (x, y, z)와 (x, -y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
∫∫∫ -x sin xy sin xz dV = 0이다. 왜냐하면, (x, y, z)와 (-x, y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
∫∫∫ -2z sin yz exp(x2 + y2 + z2) dV = 0이다. 왜냐하면, (x, y, z)와 (x, -y, z)가 절댓값은 같고 부호가 달라 서로 상쇄되기 때문이다.
그러므로 주어진 적분값은 0이다.
4. 크기가 n × n인 행렬 A = (aij)는 aij = x|i-j|로 정의된다. (단, x는 양의 실수이다.)
⑴ 행렬식 det(A)의 값을 구하여라.
⑵ 행렬 A가 가역이 되는 x를 모두 구하고, 그 때 A의 역행렬을 구하여라.
Solution.
크기가 n × n인 행렬을 An이라고 하자.
다음은 4 × 4 행렬의 행렬식을 여인수 전개에 의해 구하는 과정이다.
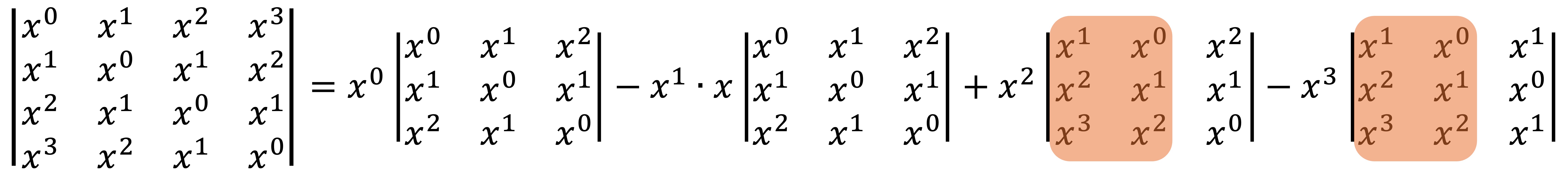
이중 색깔로 칠한 각 부분은 선형종속인 두 열벡터를 나타내고 있다.
따라서 det A4 = (1 - x2)det A3으로 나타낼 수 있고, 이를 일반화하면 det An = (1 - x2) det An-1 = (1 - x2)n-1이라 할 수 있다.
그러므로 x ≠ 1이면 A는 언제나 가역행렬이다.
A의 역행렬을 구하기 위해 다음과 같은 직관을 활용하자.
○ A와 A의 역행렬의 곱 결과 단위 행렬이 만들어지므로 대각성분과 한 칸 떨어진 대각선에만 값이 있고 나머지는 0인 행렬을 우선 고려한다. 왜냐하면, 단위행렬은 대각성분을 제외하고는 모두 0이기 때문에 대각선과 멀리 떨어진 지점에 유의한 값이 있을 것 같지 않다.
○ 프랙탈 대칭성이 있다. 즉, 임의의 대각성분 원소를 골랐을 때 그 주변의 값의 분포가 비슷하게 나타날 것이다. 단, corner case는 분명히 존재할 것이다. 이를 통해, 대각성분은 양쪽 끝이 다르고, 그것을 제외한 가운데 원소들은 모두 값이 동일하며, 한 칸 떨어진 대각선은 값이 모두 동일할 것으로 추정된다.
○ A2, A3의 역행렬을 다음과 같이 구할 수 있어서, 위 직관이 타당하며 이를 An의 역행렬로 확장할 수 있다.
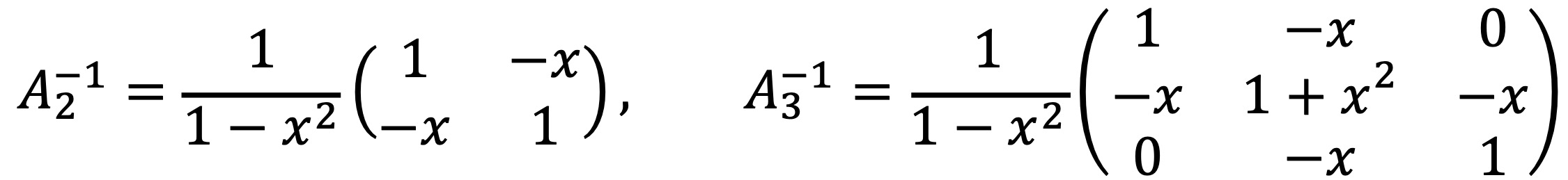
그러므로 An의 역행렬은 다음과 같다.
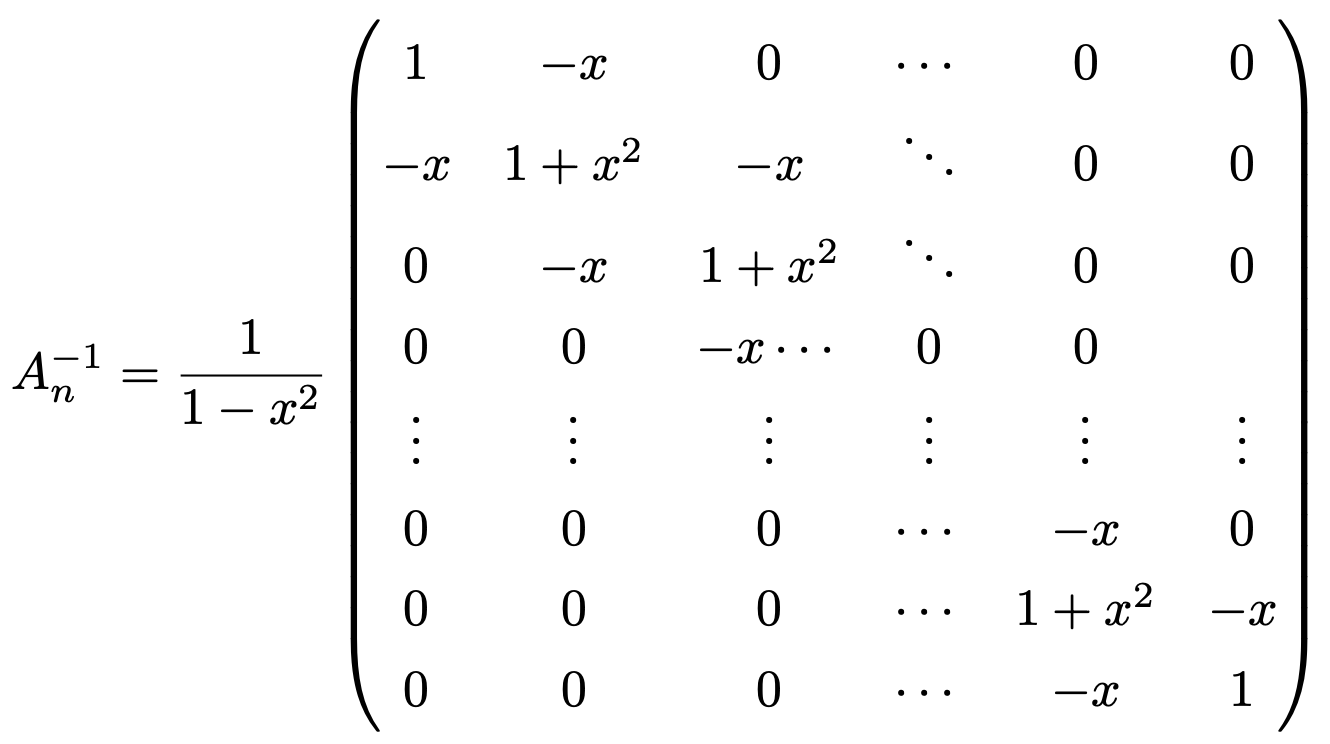
An이 상당한 대칭성이 있었는데, 이것의 역행렬도 상당한 대칭성(i.e., 프랙탈 대칭성)이 관찰됐다.
이것도 군이론의 표현 이론으로 분석할 수 있을까?
5. 크기가 n × n인 실행렬들로 이루어진 실벡터공간을 Mn(ℝ)이라 하자. 행렬 A, B ∈ Mn(ℝ)에 대하여 선형사상 LA,B : Mn(ℝ) → Mn(ℝ)을 LA,B(X) = AXB로 정의하면 det(LA,B) = det(AnBn)임을 보여라.
Solution.
2 × 2 실행렬들로 이루어진 실벡터공간 M2(ℝ)을 고려하여 준 명제를 증명하면 이 문제를 푸는 충분한 직관을 제공할 수 있다.
A의 첫 번째 열벡터를 A·,1, B의 첫 번째 행 벡터를 B1,·라 할 때 LA,B를 다음과 같이 나타낼 수 있다.
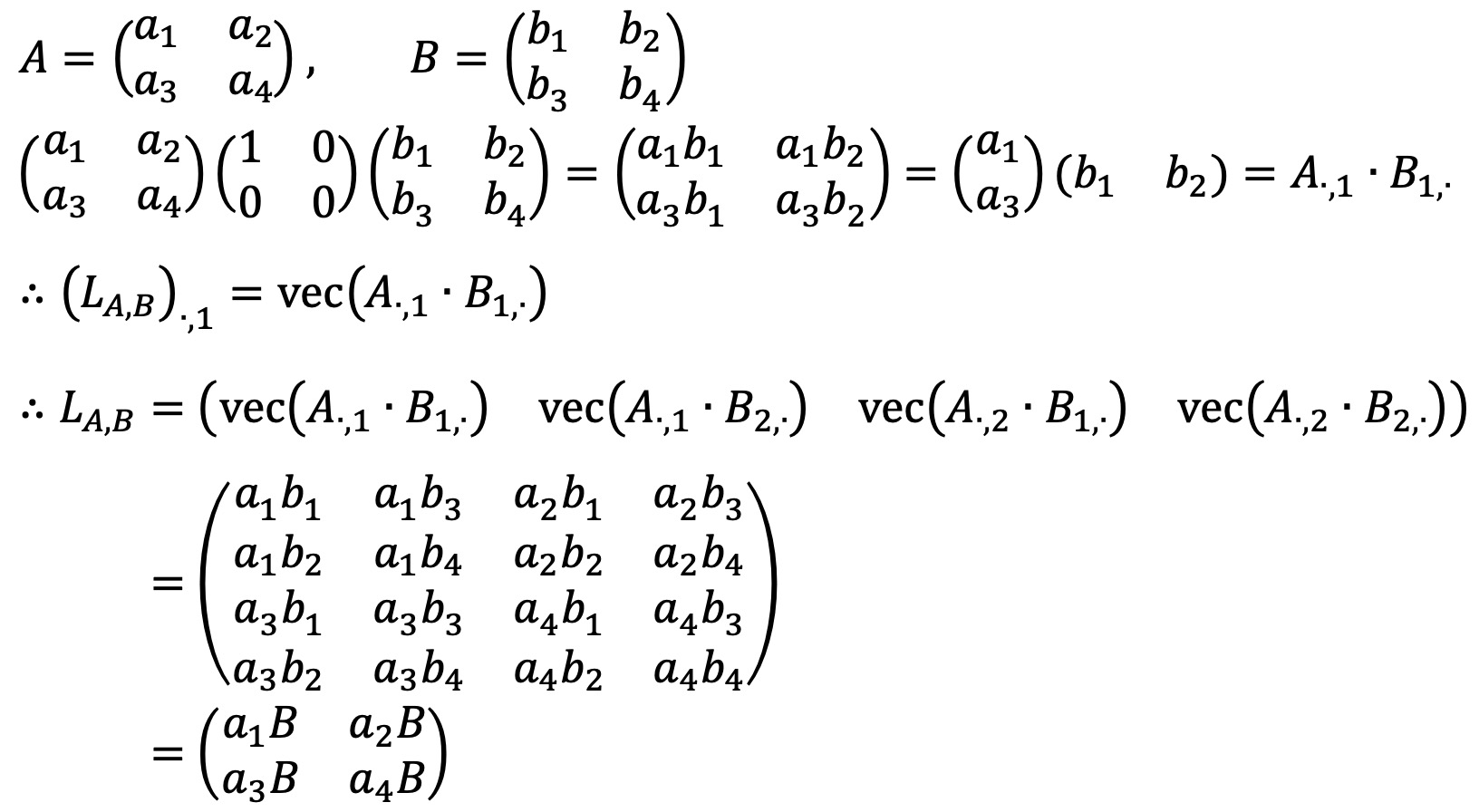
행렬식의 성질을 이용하자. n × n 행렬 A, B, C, D가 있을 때, |D| ≠ 0이고 CD = DC인 경우 다음이 성립한다.
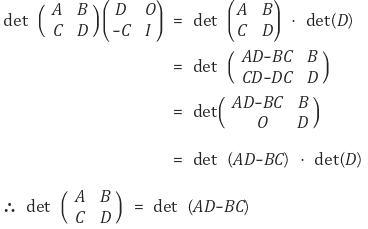
따라서 LA,B의 행렬식은 다음과 같다.
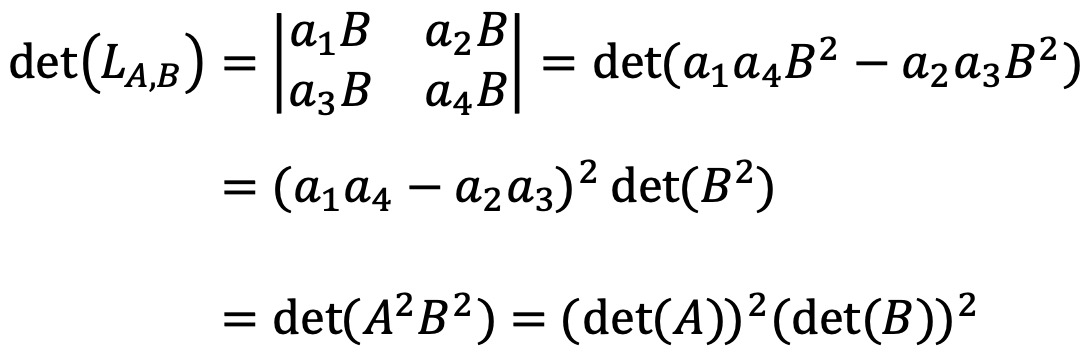
위 과정을 일반적인 n에 대하여 서술하면 준 명제를 증명할 수 있다.
6. 실수 위에서 정의된 함수 f(x) = √3 (2x + 1) / ((x2 + x + 3)2 + 3)에 대하여, 다음 급수의 값을 구하여라.
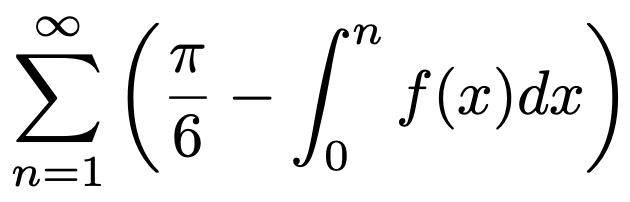
Solution.
다음 식을 찾을 수 있다.

따라서 주어진 급수는 전형적인 arctan 망원합(telecoping) 형태로 보통 다음 식을 활용한다.
arctan(a) - arctan(b) = arctan((a-b) / (1 + ab))
a = (n+1) / √3, b = n / √3을 대입하면 다음을 얻을 수 있다.
arctan((n+1) / √3) - arctan(n / √3) = arctan(√3 / (n2 + n + 3))
따라서, (준식) = arctan(∞) - arctan(1 / √3) = π/2 - π/6 = π/3 을 얻을 수 있다.
7. 벡터 v1, v2, v3, v4 ∈ ℝ4는 길이가 각각 2, 3, 4, 5이며 서로 수직이다. 임의의 2차원 부분공간 W ⊂ ℝ4에 대하여 v1, v2, v3, v4를 W에 정사영하여 얻은 벡터들 가운데 적어도 하나는 길이가 1이 아님을 보여라.
Solution.
귀류법을 사용하자. 즉, v1, v2, v3, v4를 W에 정사영하였을 때 모두 길이가 1이라고 가정하고, 모순을 이끌어내자.
4차원에서 서로 수직인 네 개의 벡터가 있으면, 이들은 사실상 ℝ4의 한 정규직교기저에서 길이만 다른 형태로 생각할 수 있다.
2차원 부분공간 W에 대한 정사영 길이가 모두 1이라는 조건을 통해 다음을 얻을 수 있다.
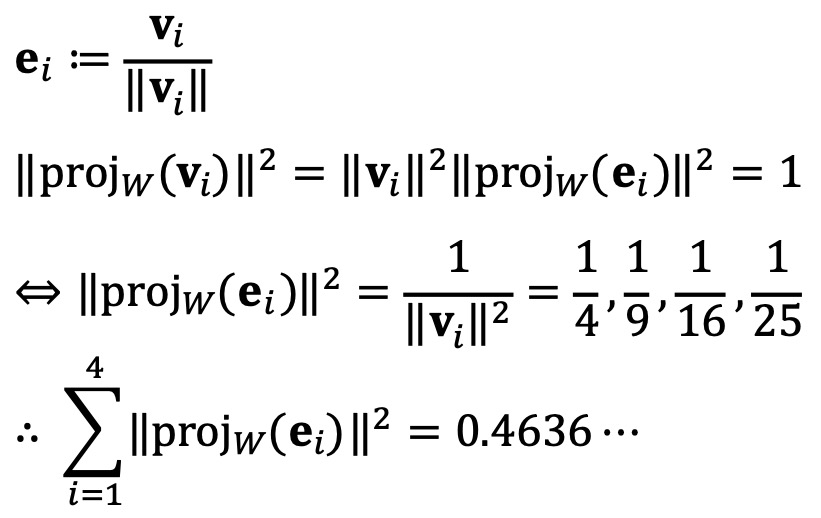
한편, 2차원 부분공간 W가 주어지면 W의 정규직교기저 w1, w2를 잡을 수 있고 각 wk를 4차원 정규직교기저에 전개하면 다음 식을 얻는다.
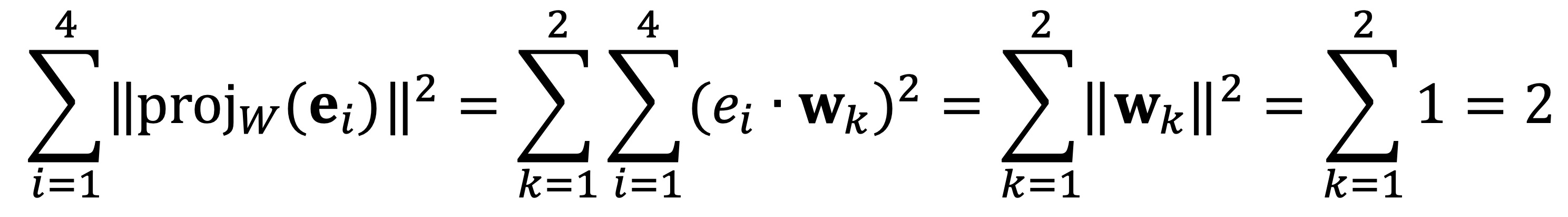
따라서 모순이 도출되었으므로, 주어진 명제가 옳다.
8. 실수 a와 정수 n (n ≥ 2)에 대하여 Sn(a)를 다음과 같이 정의하자.

수열 {Sn(a)}n≥2가 양의 실수로 수렴하는 a의 값을 모두 구하여라.
Solution.
a = 2019인 경우 다음과 같다.

그러므로 완비성 공리에 의해 Sn(a)는 n → ∞에 대하여 수렴값이 존재하고, 그 값은 양의 실수이다.
한편, a > 2019이면 Sn(a)는 무한대로 발산하고, a < 2019이면 Sn(a)는 0으로 수렴한다.

따라서 주어진 수열이 양의 실수로 수렴하는 a는 2019밖에 없다.
입력: 2024.12.28 08:36
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.01.28 |
|---|---|
| 【대수경】 제 37회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.01.06 |
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.12.29 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.08 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.12.07 |




최근댓글