13강. 휘트스톤 브릿지(휘스스톤 브릿지, Wheatstone Bridge)와 센서
추천글 : 【회로이론】 회로이론 목차
1. 휘트스톤 브릿지 회로 [목차]
⑴ (구별개념) Ballast circuit
① 수학적 분석

② 단점
○ accurate zero position 불가능
○ temperature compensation 불가능
○ poor sensitivity & accuracy
⑵ 휘트스톤 브릿지 회로 : Ballast circuit을 개선하기 위해 제안됨
Figure. 2. 휘스스톤 브릿지 개요
A-B 단자 사이에 저항 R이 연결돼 있다고 가정하자.
전지의 전압을 V, A 노드에서의 전압을 VA, B 노드에서의 전압을 VB라고 하자.
그러면 다음과 같은 KCL 식을 얻을 수 있다.
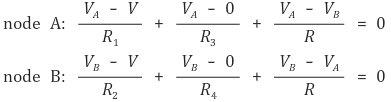
위 식을 연립하면 다음과 같은 결과를 얻는다. (단, 1/R을 G라고 정의한다.)

만약 A-B 단자가 open(G = 0)이면 각 노드에서의 전압은 다음과 같다.
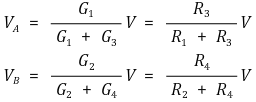
이는 예상한 대로 각각의 직렬회로(R1-R3 loop, R2-R4 loop)에서의 분압방식과 같다.
이때 각 전류는 다음과 같이 나타난다.
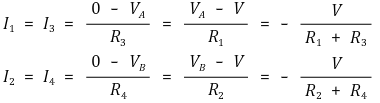
만약 A-B 단자가 Short(G = ∞)면 각 노드에서의 전압은 다음과 같다.
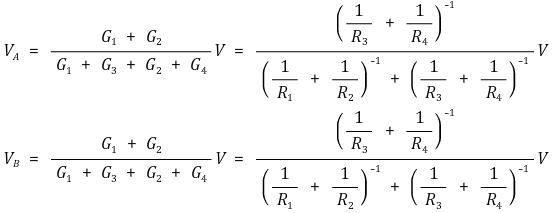
이는 2개의 병렬 회로의 직렬 회로에서 예상되는 바로 그 전압이다.
이때 각 전류를 구하는 법은 Open에서 구하는 방법과 같으므로 생략하도록 한다.
R이 임의의 값을 가질 때 노드 A에서 노드 B로 흐르는 전류는 다음과 같다.
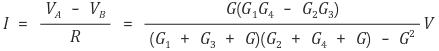
분모가 항상 양수임을 확인하자.
내부저항이 R인 검류계를 A-B 단자 사이에 연결했다고 가정하자.
이때 전류 I의 절대값이 특정값보다 크면 검류계의 바늘이 full scale을 가리킨다고 하자.
따라서 검류계의 바늘이 움직이지 않는 조건(balanced wheatstone bridge)은 다음과 같다.
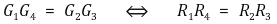
이 결론은 교류 브릿지 회로에서도 유효하다.
⑶ 휘스스톤 브릿지의 배열 : strain gauge를 중심으로 설명
① quarter bridge, half bridge (one in tension, one in compression), full bridge (two in tension, two in compression)
② possion arrangement : half bridge, full bridge 등이 있음
③ dummy method : 온도 등의 요인을 제거하기 위해 strain이 가해지지 않는 strain sensor를 배열하는 것
④ gauge method : 온도 등의 요인이 모든 sensor에 영향을 주도록 하여 그 요인을 제거하고 민감도를 높이는 것
⑷ shunt calibration : 병렬로 Rc를 연결
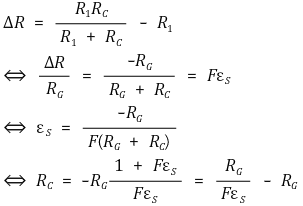
2. 센서 물리학 [목차]
⑴ 압전효과(piezoelectric effect)
① gauge factor : stain gauge는 길이 증가에 따라 metal coil의 저항값이 증가함

② Sauerbrey equation

○ f0 : resonant frequency (Hz)
○ Δf : frequency change (Hz)
○ Δm : loaded mass (g)
○ A : piezoelectrically active area (electrode area) of crystal (㎠)
○ ρq : density of quartz (2.648 g/㎤)
○ μq : shear modulus of AT-cut quartz crystal (2.947 × 1011 g/㎠·s2)
○ vq : transverse wave velocity in quartz (m/s)
⑵ 초전효과(pyroelectric effect)
⑶ 홀효과(Hall effect)
⑷ 광전도효과(photoconductive effect)
⑸ 자기탄성효과(magnetoelastic effect) : 자기장에 의해 재료의 탄성이 변하는 현상
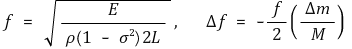
① E : modulus of elasiticity
② σ : Poisson's ratio
③ P : mass density of the sensor material
④ L : longitudinal dimension of the sensor
⑤ f : initial resonance frequency
⑥ M : initial mass
⑹ 자기저항효과(magnetoresistance effect)
⑺ 자기광학효과(magneto-optic effect)
3. 휘트스톤 브릿지 회로의 응용 [목차]
⑴ 연기 감지기(smoke detector)
연기 감지기는 화재를 감지하여 스프링클러를 가동시키기 위한 센서이다.
모든 공공건물 내 모든 방 천장에 하나씩은 꼭 설치돼 있을 것이다!
이 장치의 상세한 구조를 살펴보면 다음과 같다.
광도에 따라서 저항값이 바뀌는 가변저항 두 개가 내장돼 있다.
광원(light source)의 빛이 두 개의 거울(reflector)을 통해서 각각의 가변저항에 가해진다.
(즉, 광원의 빛은 방사상으로 퍼져 나가지만 특정 각도로 입사되는 빛만 각 저항에 도달할 수 있다.)
만약 화재가 나서 연기가 발생하면 아래쪽 거울에 반사되는 빛의 양이 줄어들게 된다.
왜냐하면 연기입자들에 의해 빛이 산란되기 때문이다.
따라서 reference cell과 smoke detector의 저항값의 차이가 유의미하게 커지면서 화재 경보를 울리게 된다.
위 도식을 회로로 나타낸 모습은 다음과 같다.
DC 전원의 전압을 V라고 하자.
Rbalance = R이라고 두면 Vbalance는 다음과 같다.
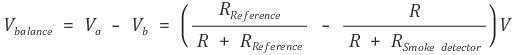
이제 아래와 같은 사실을 반영하자.
가. photoconductive cell은 광도에 선형적으로 저항값이 변한다.
나. RReference = R
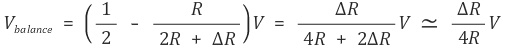
그 결과 출력 전압 Vbalance가 저항값의 변화량에 비례한다는 것을 알 수 있다.
한편 Rbalance를 가변저항으로 설정한 이유는 제작오차를 보정하기 위함이다.
⑵ 실리콘 압력 센서(silicon pressure sensor)
압력센서는 외부 힘에 따라 저항값이 변하는 압저항(The Piezoresistive)을 이용한다.
압력센서의 형태는 다음과 같이 나타난다.
이때 왼쪽그림의 편의상 9시 방향의 저항부터 시계방향으로 R1, R2, R3, R4라고 하자.
오른쪽 그림은 왼쪽 그림을 위에서 본 모습이다.
오른쪽 그림에서 두꺼운 부분의 길이가 대략 0.5 mm, Thin diaphragm의 세로 길이가 대략 1 ~ 2 nm 정도 된다.
그리고 thin diaphragm의 가로 길이는 mm 단위이다.
압력센서로 실리콘을 쓰는 이유는 실리콘이 결정구조가 좋아 KOH에 쉽게 에칭(etching)되기 때문이다.
R1과 R3의 세로방향 응력(longitudinal stress)은 R2와 R4의 가로방향 응력(transverse stress)과 같다.
R1과 R3의 가로방향 응력(transverse stress)은 R2와 R4의 가로방향 응력(longitudinal stress)과 같다.
Figure. 10. 재료와 응력표시
만일 한 저항이 σl만큼의 세로방향 응력을 받는다면, 이것은 반드시 σt = -νσl만큼의 가로방향 응력도 받는다.
여기서 ν는 포아송비(Poisson ratio)이다.
참고로, strain(ε)은 변형률로 길이의 변화량(δ)을 처음 길이로 나눠준 값이다.
압저항의 저항값은 길이와 유사한 성질을 갖는다.
즉, strain이 stress에 비례하는 것(σ = Eε, E : 탄성계수(Young's modulus))처럼 ΔR / R도 또한 Stress에 비례한다.
한편 가로방향 stress와 세로방향 stress는 독립적으로 ΔR / R에 영향을 준다.
따라서 외부 응력에 의한 R1과 R3의 변화를 다음과 같이 나타낼 수 있다.
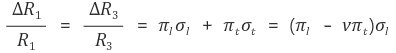
비슷하게 외부 응력에 의한 R2와 R4의 변화를 다음과 같이 나타낼 수 있다.
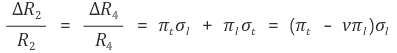
한 제품은 다음과 같은 상수의 값을 갖는다.
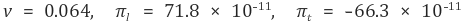
따라서
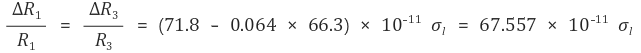

(주의 : 계산에 실수가 있을 수 있음)
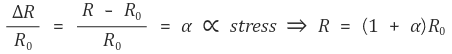
그 결과 다음과 같이 나타낼 수 있다.
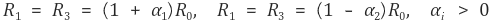
위 센서를 회로로 나타내자.
Figure. 14. 문제상황에 대한 휘트스톤 브릿지 회로
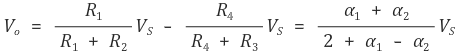
이때 α1과 α2가 0.02 혹은 더 작은 값이라는 점과 기껏해야 10 %밖에 차이나지 않는다는 점으로 인해,
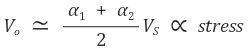
외부 압력과 응력은 비례하므로 이 센서는 압력에 비례하는 값을 출력한다.
⑶ strain gauge bridge
힘으로부터 유발되는 Strain을 측정하는 변환기로 다음과 같이 생겼다.
Figure. 15. strain gauge bridge의 구조
파란색 혹은 노란색 상자는 Strain에 따라 저항의 값이 변하는 압전지(Stress에 비례)를 나타낸다.
이때 위아래로 힘이 가해지면 장치가 다음과 같이 변형된다.
Figure. 16. strain gauge bridge의 작동 원리
파란색 상자가 놓여있던 부분이 오목해지면서 파란색 상자로 표시한 저항에 압축력이 걸린다.
또, 노란색 상자가 높여있던 부분이 볼록해지면서 노란색 상자로 표시한 저항에 인장력이 걸린다.
그 결과 파란색 상자로 표시한 저항의 저항값은 감소하고, 노란색 상자로 표시한 저항의 저항값은 증가한다.
위 장치를 회로로 표현하자.
Figure. 17. 주어진 문제 상황에 대한 휘트스톤 브릿지 회로
이러한 회로는 이미 앞서 많이 다룬 바 있으므로 다음과 같은 회로를 고려하도록 하자.
우선 브릿지 회로를 살펴보면 vi를 구할 수 있다.
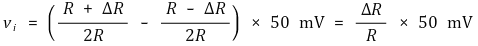
따라서 종속전압원에 의해 50 Ω 저항과 전압계가 있는 도선 양단의 전압은 ΔR ÷ R × 50b mV이다.
그런데 DMM의 경우 내부저항은 10 ~ 11 MΩ 정도이므로 다음과 같은 근사가 가능하다.
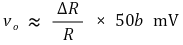
따라서 외부 Stress의 값을 증폭하는 회로를 완성하였다.
⑷ 머레이 루프법(Murray's loop method)
전기적 사고점 탐지법의 하나로서 휘스스톤 브리지의 원리를 이용하여 선로상의 고장점(1선 지락사고)을 검출하는 방법.
이 방법은 건전한 보조 귀선 1선이 필요하다.
검류계에 전류가 흐르지 않으면 평형상태이므로
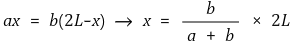
단, L : 선로의 전체 길이 (m), x : 측정점에서 고장점까지의 거리 (m)
머레이 루프법은 1선 지락 사고 및 선간 단락 사고시 측정 방법이다.
3선 단락 및 지락 사고시 측정 방법은 펄스 측정법(pulse radar)이다.
단선 사고시 측정 방법은 정전 브릿지법(capacity bridge)이다.
입력: 2016.01.06 22:05
수정: 2020.09.04 00:08
'▶ 자연과학 > ▷ 회로이론' 카테고리의 다른 글
| 【회로이론】 10-1강. 부유 커패시터와 Op Amp의 피드백 방향 (0) | 2016.06.27 |
|---|---|
| 【회로이론】 회로이론 응용 : Logic Probe (0) | 2016.06.27 |
| 【회로이론】 12강. 직류회로이론 (0) | 2016.06.27 |
| 【회로이론】 5강. 스위치, 퓨즈, 접지, d'Arsonval meter (0) | 2016.06.27 |
| 【회로이론】 3강. 저항 (0) | 2016.06.27 |























최근댓글