3강. 조합논리(combinational logic)
추천글 : 【논리설계】 논리설계 목차
1. 논리회로 소자 [본문]
2. 논리회로 구현 [본문]
3. 논리회로 개선 1. 불 대수학 [본문]
4. 논리회로 개선 2. two-level simplification [본문]
1. 논리회로 소자 [목차]
⑴ Y를 출력, X, A, B를 입력이라고 가정
⑴ 종류 1. 버퍼 게이트(buffer gate) : 전송 게이트라고도 함. Y = X
① 논리적 의미를 가지지 않으나 통신 분야 등에서 사용됨
② 구현 1. BJT 트랜지스터를 통한 구현 (TTL, transistor-transistor logic)
○ vi = ON인 경우 : 트랜지스터 스위치가 ON이 되므로 vcc의 전압이 vo로 통함
○ vi = OFF인 경우 : R1으로 전류가 흐르지 않으므로 vo = 0
Figure. 1. 이미터 팔로워를 이용한 전압 팔로워
③ 구현 2. NOT gate를 통한 LED 버퍼 게이트 구현
○ vi = ON인 경우 : 인버터의 출력단자가 OFF이므로 LED에 전류가 흘러 LED가 발광함
○ vi = OFF인 경우 : 인버터의 출력단자가 ON이므로 LED에 전류가 흐르지 않아 LED가 발광하지 않음
Figure. 2. NOT gate를 이용한 LED 버퍼 게이트의 구현
④ 구현 3. BJT 트랜지스터를 이용한 구현 (TTL, transistor-transistor logic)
○ vi = ON인 경우 : Q1 다이오드가 OFF이고 Q2에 베이스 전류 및 컬렉터 전류가 흐르지 않아 Vcc가 곧장 인가됨
○ vi = OFF인 경우 : Q1 다이오드가 ON이고 Q2가 ON이 되어 vo에 접지가 연결됨
Figure. 3. BJT 트랜지스터를 이용한 NOT gate의 구현
⑤ 구현 4. 다이오드와 BJT 트랜지스터를 이용한 구현 (DTL, diode-transistor logic)
○ vi = ON인 경우 : Q1 OFF → Q2 OFF → Q4 OFF → Vcc - Q3의 vBE 전압 - D1의 문턱전압만큼 vo에 인가됨
○ vi = OFF인 경우 : Q1 ON → Q2 ON → Q4 ON → 접지가 vo에 인가됨
○ 다이오드의 역할 : Q2와 Q4가 ON일 때 Q3가 ON이 되는 것을 방지함
Figure. 4. 다이오드와 BJT 트랜지스터를 이용한 NOT gate의 구현
⑥ 구현 5. 3 상태 제어선, 다이오드, BJT 트랜지스터를 이용한 구현
○ TSL circuit(tri-state logic circuit) : gate가 high state, low state, high-impedance state 등 세 가지 상태를 가짐
○ 3 상태 제어선이 HIGH : 입력이 ON이면 출력은 HIGH (inverter 기능)
○ 3 상태 제어선이 LOW : 출력선은 LOW도 HIGH도 아닌 floating 상태 (high-impedance state)
○ high-impedance 상태에서는 TTL 출력 핀과 내부 회로가 절연됨
○ 사용하지 않을 때 TTL과 접속회로를 분리해 둠
Figure. 5. 상태 제어선, 다이오드, BJT 트랜지스터를 이용한 NOT gate의 구현
⑶ 종류 2. NOT gate : 인버터(inverter)라고도 함. Y = X'
Figure. 6. NOT gate의 기호
① 구현 1. BJT 트랜지스터를 통한 구현 (TTL, transistor-transistor logic)
○ vi = ON인 경우 : 트랜지스터 스위치가 ON이 되므로 vo = 0
○ vi = OFF인 경우 : R1으로 전류가 흐르지 않으므로 vo = Vcc
Figure. 7. BJT 트랜지스터를 이용한 NOT gate의 구현
② 구현 2. BJT 트랜지스터를 통한 구현 (개선) (TTL, transistor-transistor logic)
○ vi = OFF일 때 확실하게 트랜지스터를 OFF 시키기 위해 별도의 전원을 연결함
Figure. 8. BJT 트랜지스터를 이용한 NOT gate의 구현
③ (참고) 구현 3. CMOS 트랜지스터를 이용한 구현
○ pMOS 1개와 nMOS 1개가 필요함
○ VHigh 또는 VLow에 저항이 연결돼 있음 : 만에 하나 스위치가 동시에 닫혀도 문제되지 않음
Figure. 9. CMOS를 이용한 NOT gate의 구현
④ 예 : IC 7404, IC 7416
⑷ 종류 3. AND gate : Y = A · B
Figure. 10. AND gate 기호
① 구현 1. 다이오드를 이용한 구현
○ A와 B 모두 ON인 경우 : R1에 전류가 흐르지 않으므로 vo = Vcc
○ A와 B 중 하나라도 ON이 아닌 경우 : OFF인 단자의 다이오드가 도통 상태가 되어 vo = OFF가 됨
Figure. 11. 다이오드를 이용한 AND gate의 구현
② 구현 2. BJT 트랜지스터를 이용한 구현 (TTL, transistor-transistor logic)
○ A와 B 모두 ON인 경우 : 두 트랜지스터가 ON이 되므로 vo = Vcc
○ A와 B 중 하나라도 ON이 아닌 경우 : 하나 이상의 트랜지스터가 OFF이므로 R3에 전류가 흐르지 않아 vo = 0
Figure. 12. BJT 트랜지스터를 이용한 AND gate의 구현
③ (참고) 구현 3. NOT gate와 NAND gate로 구현 : 총 6개의 CMOS 트랜지스터가 필요
Figure. 13. NOT gate와 NAND gate를 이용한 AND gate의 구현
④ 예 : IC 7408
⑸ 종류 4. OR gate : Y = A + B
Figure. 14. OR gate 기호
① 구현 1. 다이오드를 이용한 구현
○ A와 B 중 하나라도 ON인 경우 : 그 다이오드가 도통되면서 vo에도 ON에 해당하는 전압이 인가됨
○ A와 B 모두 OFF인 경우 : R4에 전류가 흐르지 않으므로 vo = 0
Figure. 15. 다이오드를 이용한 OR gate의 구현
② 구현 2. BJT 트랜지스터를 이용한 구현 (TTL, transistor-transistor logic)
○ A와 B 중 하나라도 ON인 경우 : 그 트랜지스터가 ON이 되므로 Vcc가 vo에도 인가됨
○ A와 B 모두 OFF인 경우 : R1에 전류가 흐르지 않으므로 vo = 0
Figure. 16. BJT 트랜지스터를 이용한 OR gate의 구현
③ (참고) 구현 3. NOT gate와 NOR gate로 구현 : 총 6개의 CMOS 트랜지스터가 필요
Figure. 17. OR gate 회로도
④ 예 : IC 7432
⑹ 종류 5. NAND gate : Y = (A·B)' = A' + B'
Figure. 18. NAND gate 기호
① 구현 1. BJT 트랜지스터를 이용한 구현 (TTL, transistor-transistor logic)
○ A와 B가 모두 ON인 경우 : 트랜지스터가 모두 ON이므로 vo는 접지와 연결됨
○ A와 B 중 하나라도 OFF인 경우 : R1에 흐르는 전류가 0이므로 vo = Vcc
Figure. 19. BJT 트랜지스터를 이용한 NAND gate의 구현
② 구현 2. 다이오드와 BJT 트랜지스터를 이용한 구현 (DTL, diode-transistor logic)
○ A와 B가 모두 ON인 경우 : D3 다이오드가 도통 상태이고 Q1 트랜지스터가 ON이므로 vo는 접지와 연결됨
○ A와 B 중 하나라도 OFF인 경우 : D1 또는 D2가 도통 상태이고 D3가 차단 상태이므로 R2에 전류가 흐르지 않음
Figure. 20. 다이오드와 BJT 트랜지스터를 이용한 NAND gate의 구현
③ (참고) 구현 3. CMOS 트랜지스터를 이용한 구현
○ VHigh 또는 VLow에 저항이 연결돼 있음 : 만에 하나 스위치가 동시에 닫혀도 문제되지 않음
○ 병렬로 연결된 한 쌍의 pMOS와 직렬로 연결된 한 쌍의 nMOS가 필요함
○ (참고) pMOS는 병렬, nMOS는 직렬로 유지하면 다중 입력에 대한 NAND gate를 구현 가능
Figure. 21. CMOS를 이용한 NAND gate 회로도
④ 예 : IC 7400 (2-input), IC 7402 (4 2-input), IC 7410 (3-input), IC 4011
⑺ 종류 6. NOR gate : Y = (A + B)' = A'·B'
Figure. 22. NOR gate 기호
① 구현 1. BJT 트랜지스터를 이용한 구현 (TTL, transistor-transistor logic)
○ A와 B 중 하나라도 ON인 경우 : 그 트랜지스터가 ON이 되어 vo와 접지가 연결됨
○ A와 B 모두 OFF인 경우 : R3에 전류가 흐르지 않으므로 vo = Vcc
Figure. 23. BJT 트랜지스터를 이용한 NOR gate 구현
② 구현 2. 다이오드와 BJT 트랜지스터를 이용한 구현 (DTL, diode-transistor logic)
Figure. 24. 다이오드와 BJT 트랜지스터를 이용한 NOR gate 구현
③ (참고) 구현 3. CMOS 트랜지스터를 이용한 구현
○ VHigh 또는 VLow에 저항이 연결돼 있음 : 만에 하나 스위치가 동시에 닫혀도 문제되지 않음
○ 직렬로 연결된 한 쌍의 pMOS와 병렬로 연결된 한 쌍의 nMOS, 총 4개의 트랜지스터가 필요
○ (참고) pMOS는 직렬, nMOS는 병렬로 유지하면 다중 입력에 대한 NOR gate를 구현 가능
Figure. 25. CMOS를 이용한 NOR gate 회로도
⑻ 종류 7. XOR gate (exclusive-OR gate) : Y = A'·B + A·B' = A⊕B
Figure. 26. XOR gate 기호
① (참고) 구현 1. CMOS를 이용한 구현
Figure. 27. CMOS를 이용한 XOR gate 회로도
② (참고) 구현 2. PTL logic circuit
○ 2개의 pass transistors, 1 NOT gate. 따라서 총 4개의 트랜지스터가 필요
○ 끝에 Buffer gate(2 transistors)를 붙이는 것을 권장
Figure. 28. PMOS를 이용한 XOR gate 회로도
③ (참고) 구현 3. NAND gate를 이용한 구현
Figure. 29. 4개의 NAND gate를 이용한 XOR gate 회로도
④ (참고) 구현 4. NOR gate를 이용한 구현
Figure. 30. 5개의 NOR gate를 이용한 XOR gate 회로도
⑤ 예 : IC 7486
⑼ 종류 8. XNOR gate (exclusive-NOR gate, NXOR gate) : Y = XY + X'·Y' = X⊙Y
Figure. 31. XNOR gate 기호
① 구현 1. CMOS 트랜지스터를 이용한 구현
② 구현 2. XOR 게이트를 이용한 구현
Figure. 32. 4개의 NOR gate를 이용한 XNOR gate 회로도
⑽ 종류 9. AOI : AND gate + OR gate + Inverter
① 6개의 트랜지스터가 필요
② 회로도
Figure. 33. AOI 회로도
2. 논리회로 구현 : 대개 2단계 논리회로(two-level logic circuit)로 구현 [목차]
⑴ 최소항(minterm), 최대항(maxterm)
| x | y | z | minterm | maxterm |
| 0 | 0 | 0 | x'·y'·z' | x + y + z |
| 0 | 0 | 1 | x'·y'·z | x + y + z' |
| 0 | 1 | 0 | x'·y·z' | x + y' + z |
| 0 | 1 | 1 | x'·y·z | x + y' + z' |
| 1 | 0 | 0 | x·y'·z' | x' + y + z |
| 1 | 0 | 1 | x·y'·z | x' + y + z' |
| 1 | 1 | 0 | x·y·z' | x' + y' + z |
| 1 | 1 | 1 | x·y·z | x' + y' + z' |
Table. 1. minterm, maxterm
⑵ SOP, POS
A B C Out
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
① SOP(sum of products) : output이 1인 ON-set을 중심으로 minterm의 합으로 표시
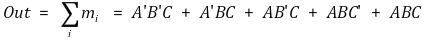
② POS(products of sum) : output이 0인 OFF-set을 중심으로 maxterm의 곱으로 표시

③ SOP 또는 POS (AND-OR circuit)로 모든 논리회로를 구현할 수 있음
④ standard SOP, standard POS : 가장 길게 표현한 것으로 이해해도 됨
⑤ SOP, POS가 중요한 이유 : 다단계 게이트는 속도가 느림 → 중요 부분은 2단계 조합논리회로 형식을 취함
⑶ 보편 논리 요소(universal logic element)
① 정의 : 홀로 모든 논리회로를 구현할 수 있는 게이트
② 중요성 : 경제적으로 저렴한 회로를 만들 수 있음
○ 한 종류의 게이트 여러 개를 패키지로 파는 경우가 많음
○ 여러 종류의 게이트를 패키지로 파는 경우는 드묾
③ 예 1. NAND
○ NOT gate 구현 : x' = x NAND x
○ AND gate 구현 : x · y = (x NAND y)'
○ OR gate 구현 : x + y = (x' · y')'
④ 예 2. NOR
○ NOT gate 구현 : x' = x NOR x
○ OR gate 구현 : x + y = (x NOR y)'
○ AND gate 구현 : x · y = (x' + y')'
⑤ 예 4. AOI
○ NOT gate 구현 : (A · A + A)' = (A + A)' = A
○ OR gate 구현 : ((A · A + B)')' = A + B
○ AND gate 구현 : (A' · A' + B')' = AB
⑥ 다른 gate는 홀로 NOT, OR, AND 등을 모두 구현할 수 있는가?
○ XOR은 universal gate가 아님
○ k개의 XOR gate로 구현할 수 있는 조합이 S = {0, A, B, A ^ B}라 하자.
○ 이때 k + 1개의 XOR gate로 구현할 수 있는 조합을 구하고자 한다.
○ 그런데 XOR gate는 교환·결합법칙이 성립하므로 1개와 k개의 연산으로 분리할 수 있다.
○ 하지만 A, B, S를 가지고 만들 수 있는 조합의 집합은 결국 S가 된다.
○ 따라서 XOR gate는 universal하지 않다.
○ AND, OR는 universal gate가 아님 (∵ NOT을 구현하지 못함)
⑷ active high activation
① 기본적인 논리설계를 변경하는 게 아니라 출력이 HIGH일 때만 반응하도록 추가적으로 연결한 회로
② 저항 R은 LED, 부저 등을 나타내고, 다이오드에 의해 출력이 HIGH일 때만 전류가 흐름
Figure. 34. active high activation
⑸ active low activation
① 기본적인 논리설계를 변경하는 게 아니라 출력이 LOW일 때만 반응하도록 추가적으로 연결한 회로
② 저항 R은 LED, 부저 등을 나타내고, 다이오드에 의해 출력이 LOW일 때만 전류가 흐름
Figure. 35. active low activation
3. 논리회로 개선 1. 불 대수학(Boolean Algebra) [목차]
⑴ 불 대수학의 정리
① identity

② null

③ idempotency

④ involution
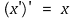
⑤ complementarity

⑥ commutativity

⑦ associativity

⑧ distributity

⑨ uniting

⑩ absorption

⑪ factoring
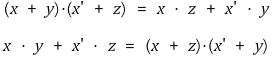
⑫ concensus
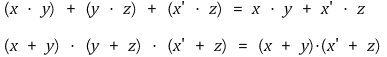
⑬ de Morgan's

⑭ generalized de Morgan's

⑵ 불 대수학을 활용한 단순화 예시(비체계적 방법)
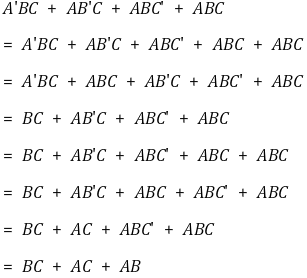
⑶ NAND-NOR circuit
① AND 대신 NAND, OR 대신 NOR로 전환(with de Morgan's law)하는 게 더 경제적이다.
② S-o-P 변환
Figure. 36. AND-OR 회로(SoP)를 NAND-NOR 회로로 바꾸는 과정
③ P-o-S 변환
Figure. 37. AND-OR 회로(PoS)를 NAND-NOR 회로로 바꾸는 과정
4. 논리회로 개선 2. two-level simplification (체계적 방법) [목차]
⑴ 개요
① 정의 : 가장 단순한 2단계 논리회로를 찾아내기 위한 방법론
○ 주로 SOP 2단계 논리회로를 찾아내기 위함
○ XOR, XNOR은 기본적으로 고려하지 않음 (그래도 가능하면 고려하자.)
○ NAND, NOR도 NAND-NOR circuit로 변환 시에만 고려됨
② 목적 : line 수 감소, gate 수 감소, stage 수 감소 (∵ stage 수가 적을수록 동기화가 잘 됨)
③ 가장 단순한 해를 보장하는 알고리즘을 찾는 문제는 NP-hard : 현재로선 풀 수 없음
⑵ 용어의 정의
① implicant: 1 (ON-set) 또는 x (don't-care)를 포함하는 서브그룹
Figure. 38. implicant를 설명하는 K-map의 예시
○ implicant는 암묵적으로 카르노맵 상의 직사각형 영역으로 정의된다.
○ 위 맵 상에서 총 6개의 직사각형이 있으므로, 6개의 implicant가 있는 것이다.
② prime implicant: 주어진 set에서 다른 어떤 implicant에도 포함되지 않는 impliant
Figure. 39. PI를 설명하는 K-map의 예시
○ 한 칸짜리는 다른 큰 직사각형에 둘러싸이므로 prime implicant가 아니다.
○ 위 4개의 직사각형 중 어느 두 개도 포함관계에 있지 않으므로 모두 prime implicant이다.
③ essential prime implicant: 모든 implicant 조합에서 꼭 포함되는 prime implicant
Figure. 40. EPI를 설명하는 K-map의 예시
○ 위 5개의 implicant 중에서 가운데 있는 implicant는 굳이 필요하지 않다.
○ 따라서 essential prime implicant는 4개이다.
⑶ Boolean cube (추천하지 않음)
① n-cube : 입력이 n 비트인 경우 n 차원의 cube를 고려한다.
② 장점 : 어떤 implicant가 불 대수 단순화가 가능한지 직관적으로 알 수 있음
Figure. 42. Boolean cube 방법의 도식
○ n-cube에서 m 차원의 subcube가 발견되면 그것은 n-m 개의 문자로 구성된다.
○ 주어진 3-cube에 (1,1,1), (1,0,1)로 이뤄진 subcube는 A, B, 두 문자로 구성된다.
③ 단점 : 4차원 이상부터는 그림을 그리거나 머릿속에서 상상하는 게 좀처럼 어렵다.
⑷ 카르노맵(Karnaugh map)
① 정의 : SOP를 보기 좋게 나타낼 수 있도록 Maurice Karnaugh가 제안한 도식
② gray code
○ 00, 01, 11, 10, 00, ···과 같이 순환하는 수열
○ 2차원 표를 구성할 때, 각 변에는 gray code가 오도록 함
○ gray code를 배치하면 implicant를 쉽게 찾을 수 있다는 장점이 있음
○ (참고) 필자는 굳이 gray code를 배치해야 하는가에 의문을 표함
③ 장점 : boolean cube와 원리는 동일하나 평면으로 펼쳐서 비교적 높은 차원까지 가능
④ 예제 1
○ 기본적으로 two-level simplification은 2단계 논리회로 중 S-o-P를 주로 쓴다.
④ 예제 2 : don't-care의 활용
○ don't-care는 절대 발생하지 않는 상황이므로 논리회로에 포함하든, 않든 don't care.
○ 따라서 중간에 있는 don't-care만 취해서 논리회로를 구성했다.
○ 논리식 = C'D + A'D (two-level simplification) = (C' + A')D (boolean algebra)
⑤ algorithm scheme
○ 1st. ON-set, DC-set, OFF-set에 대한 진리표를 작성
○ 2nd. 임의의 한 ON-set에서 가능한 prime implicant를 모두 표시하기
○ 3rd. 남아 있는 ON-set 중에서 임의로 골라 가능한 prime implicant를 모두 표시
○ 4th. 남아 있는 ON-set 중에서 임의로 골라 가능한 prime implicant를 모두 표시
○ 5th. essential prime implicant를 먼저 찾아내기
○ 6th. 남아 있는 ON-set을 포함할 수 있는, 최적의 prime implicant set을 선택
○ 임의성 때문에 최적의 해를 보장할 수 없음
③ 단점 : 높은 차원에서는 한계가 있음
○ 5-variables
Figure. 47. 5개의 변수에 대한 K-map (3D)
Figure. 48. 5개의 변수에 대한 K-map (2D)
○ 6-variables, 7-variables
Figure. 49. 6개, 7개의 변수에 대한 K-map
○ 제언 : 가로, 세로에 gray code가 아닌 크기 순으로 수를 적으면 차원의 한계 ↓
○ 그러나 높은 차원에서 카르노맵을 그리면 직관적으로 implicant를 찾기 어려움
⑸ CAD Tools(Quine-McCluskey method; QM method)
① 1st. 주어진 S-o-P에서 모든 prime implicant 찾기
○ 1st - 1st.
Table. 2. QM method 과정 (1-1)
○ 1st - 2nd.
Table. 3. QM method 과정 (1-2)
○ 1st - 3rd.
Table. 4. QM method 과정 (1-3)
○ 1st - 4th. prime implicant는 취소선이 쳐지지 않은 항들이다.
② 2nd. PI chart를 이용하여 prime implicant의 최적의 조합을 찾음
○ 2nd - 1st.
Table. 5. QM method 과정 (2-1)
○ 2nd - 2nd.
Table. 6. QM method 과정 (2-2)
○ 2nd - 3rd.
Table. 7. QM method 과정 (2-3)
○ essential하지 않은 PI 중 최선의 조합을 찾아내는 과정은 brute-force로 진행된다.
○ 이 상황에서 여러 heuristic 알고리즘이 적용된다. (최고의 효율성의 보장 ↓)
○ 2nd - 4rd. 논리식 = B'C' + CD' + A'BD
③ don't-care 조건이 관여하는 경우
○ 1st. don't-care를 모두 1로 보고 PI chart를 완성한다.
○ 2nd. prime implicant의 조합을 찾는 과정에서 don't-care는 무시한다.
Table. 8. don't-care 조건을 이용한 QM method 과정
○ 예를 들어, 6, 7, 8이 don't-care인 경우이다.
○ 이 chart에서 4.5.2.1.을 진행한다.
⑹ Esspresso Method : 그 에스프레소가 맞다.
입력: 2016.09.23 01:58
수정: 2020.03.31 21:23
'▶ 자연과학 > ▷ 논리설계' 카테고리의 다른 글
| 【논리설계】 4강. 조합논리의 파형 (0) | 2016.09.23 |
|---|---|
| 【Logic Design】 2-bit comparator (0) | 2016.09.17 |
| 【Logic Design】 door_lock (0) | 2016.09.11 |
| 【Logic Design】 days_of_the_month (0) | 2016.09.11 |
| 【논리설계】 2강. 논리설계의 기초 (0) | 2016.09.06 |





























































최근댓글