【화학】 2023 MEET/DEET 화학
2023 MEET/DEET 화학
추천글 : 【화학】 MEET/DEET 화학 풀이
두둘 님 지적사항 수정 (23.08.01)
화학 님 질의사항 반영 (24.07.17)
1. 그림은 주양자수(n)가 3 이하인 수소 원자 오비탈 ㈎ ~ ㈐의 방사 방향 파동 R(r)를 나타낸 것이다. 이에 대한 설명으로 옳지 않은 것은?
⑴ 문제


⑵ 풀이 : ①
① f(r) = 4πr2 R(r)이므로, ㈎, ㈏, ㈐에서 f(r)은 r = 0에서 0의 값을 가짐

② 마디의 개수 공식 : n ≤ 3이고 방사방향 마디 개수(n - ℓ - 1)가 0이며 구형이 아니므로(ℓ ≠ 0), 2p, 3d 오비탈이 있을 수 있음. ㈏, ㈐를 비교하면 ㈏는 2p이므로 마디 개수는 n-1 = 1
③ ②의 논의에서와 같이 ㈐는 3d이므로 각운동량 양자수(ℓ)는 2
④ ㈏와 에너지 준위가 같은 오비탈은 2s, 2p이고 ㈐와 에너지 준위가 같은 오비탈은 3s, 3p, 3d (축퇴 깨짐 없음)
⑤ 보어 모델 : ㈎는 구형이고 방사방향 마디 개수(n - ℓ - 1)가 0이므로, ㈎는 1s. ㈎, ㈏의 에너지 준위 차이는 R(1 - 1/4) = 3R/4이고, ㈏, ㈐의 에너지 준위 차이는 R(1/4 - 1/9) = 5R/36
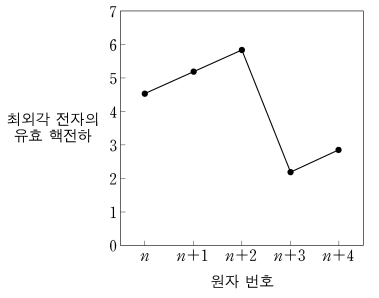
2. 그림은 2, 3주기 원소의 일부에 대해 최외각 전자의 유효 핵전하를 나타낸 것이다. 원소의 바닥 상태 원자에 대한 설명으로 옳은 것은?
⑴ 문제

⑵ 풀이 : ⑤
① 같은 주기에서 원자 번호가 증가함에 따라 최외각 전자의 유효 핵전하가 증가하므로 (n+2)번 원자는 주기가 바뀌기 직전인 Ne
② 전자친화도는 대체로 주기율표에서 오른쪽 위로 갈수록 큼
③ 원자 반지름은 주기가 클수록 족이 작을수록 크므로 (n+3)번 원자인 Na가 (n+2)번 원자인 Ne보다 큼
④ 결국 (n+2)번 원자와 (n+3)번 원자의 제1 이온화 에너지를 비교하는 문제인데, (n+2)번 원자는 비활성 기체인 Ne이고 (n+3)번 원자는 알칼리 금속인 Na임. 따라서 (n+2)번 원자가 (n+3)번 원자보다 제1 이온화 에너지가 크고, 그래서 (n+3)번 원자가 (n+4)번 원자보다 제2 이온화 에너지가 큼
⑤ 같은 주기에서 원자 번호가 증가함에 따라 최외각 전자의 유효 핵전하가 증가
3. 다음은 C2H2, N2H2, H2O2 분자에 대해 원자의 결합 순서를 각각 나타낸 것이다. 가장 타당한 루이스 구조를 근거로, 원자가 껍질 전자쌍 반발 이론과 원자가 결합 이론을 적용하여 이에 대해 설명한 것으로 옳지 않은 것은?
⑴ 문제
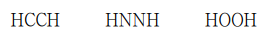

⑵ 풀이 : ④
① C2H2는 H-C≡C-H이므로 sp 혼성
② C2H2에서 탄소의 원자가 전자는 4, 비공유 전자쌍의 수는 0, 결합수는 4이므로 형식 전하 = 4 - 0 - 4 = 0
③ N2H2는 H-N=N-H이므로 sp2 혼성이고, 그래서 모든 원자가 한 평면에 있음
④ H2O2는 H-O-O-H이므로 이중결합, 삼중결합이 없으므로 모두 σ 결합
⑤ N2H2에서의 ∠HNN은 약 120°이고, H2O2에서의 ∠HOO은 약 108.5°
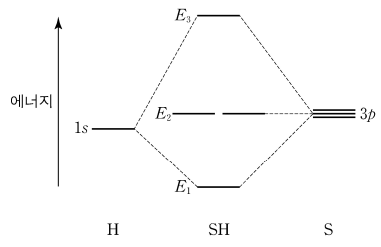
4. 그림은 S과 H의 원자 오비탈로부터 만들어진 SH 분자 오비탈의 에너지 준위 일부를 나타낸 것이다. 이 그림을 이용하여 바닥 상태의 SH, SH-에 대해 설명한 것으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제

⑵ 풀이 : ④
ㄱ. E3 (σ*s-p)의 마디 개수는 2개, E1 (σs-p)의 마디 개수는 1개
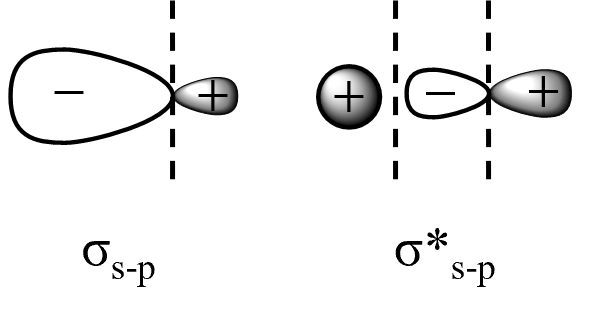
ㄴ. SH 분자 오비탈에 H로부터 1개, S로부터 4개 전자를 채워야 하므로 H의 1s보다 높은 E2 오비탈에 전자가 채워짐
ㄷ. E1은 결합 오비탈, E2는 비결합 오비탈, E3는 반결합 오비탈이고, SH에서 전자 하나가 추가될 때 E2에 추가되므로 결합차수에 영향을 주지 않음
결합 차수 = (결합 전자 수 - 반결합 전자 수) / 2
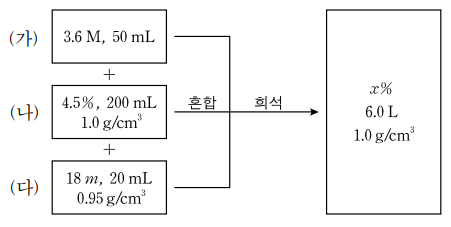
5. 그림은 분자량이 50인 A의 수용액 ㈎ ~ ㈐를 모두 혼합한 후, 물로 희석하여 x% 용액 6.0 L를 만드는 과정을 나타낸 것이다. 이에 대한 설명으로 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제

⑵ 풀이 : ③
ㄱ. 3.6 mol/L × 50 mL × 50 g/mol = 9 g
ㄴ. 용액 질량 = 200 mL × 1.0 g/mL = 200 g이므로, (200 × 0.045 × 1/50) / (200 × 0.955 × 10-3) = 0.9424 m
ㄷ. 용액 질량 = 6000 mL × 1.0 g/mL = 6000 g이고 ㈐에서 용매가 1 kg, A가 18 mol 녹아 있을 때 용액은 1.9 kg 몰랄 농도가 18 m이므로, x = (9 + 200 × 0.045 + 20 × 0.95 / 1900 × 18 × 50) / (6000 × 1) × 100 = 0.45 (%)
6. 다음은 A(g)와 B(g)로부터 C(g)가 생성되는 반응의 균형식이다.
aA(g) + bB(g) → 2C(g)
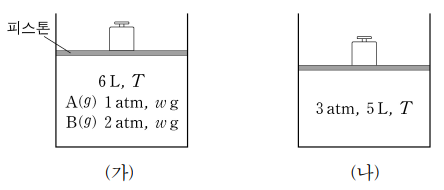
그림 ㈎는 온도 T에서 피스톤이 달린 실린더에 A(g)와 B(g)가 들어 있는 초기 상태를, ㈏는 한계 반응물이 소진되어 반응이 완결된 상태를 나타낸 것이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 기체는 이상 기체로 거동한다.)
⑴ 문제

⑵ 풀이 : ③
ㄱ. 혼합 기체의 밀도 = 전체 질량 / 전체 부피 = 2w / 5 = 0.4w g/L (∵ 질량 보존의 법칙)
ㄴ. 온도가 일정할 때 몰수는 P × V처럼 계산하여 풀 수 있어서, 반응 전 A는 6, B는 12이고 반응 후 전체는 15라고 할 수 있다. A 또는 B가 전부 반응하였고 일반적으로 a, b는 자연수 혹은 반정수이므로, 쉽게 A : 6 → 0 (a = 2), B : 12 → 9 (b = 1), C : 0 → 6 (c = 2)을 찾아낼 수 있다. 따라서 PC = 6 / 5 = 1.2 atm이 성립한다. 해의 유일성에 대한 증명은 생략한다.
ㄷ. 온도가 일정할 때 몰 수는 P × V처럼 계산하여 풀 수 있어서, ρA = w / 6, ρB = w / 12, ρC = ρA + ρB / 2 = ρA × 1.25
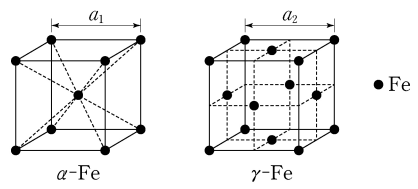
7. 철(Fe)은 상온에서 α-Fe 구조를 갖고, 고온에서 γ-Fe 구조를 갖는다. 그림은 α-Fe, γ-Fe의 입방 단위 세포를 각각 나타낸 것이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 원자 간 최단 거리는 α-Fe에서와 γ-Fe에서가 같다.)
⑴ 문제

⑵ 풀이 : ②
ㄱ. 금속 결정 : α-Fe의 배위수는 8, γ-Fe의 배위수는 12
ㄴ. 원자 간 최단 거리를 d라고 할 때, √3 × a1 = 2d, √2 × a2 = 2d가 성립
ㄷ. ρα-Fe = 2 × ρFe / a13 = 16 ρFe / (3√3 d3), ργ-Fe = 4 × ρFe / a23 = 16√2 ρFe / d3 → ργ-Fe = ρα-Fe × 3√6
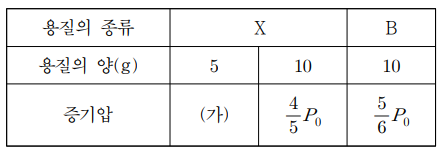
8. 표는 온도 T에서 10 g의 휘발성 액체 A에 비휘발성 용질 X, 또는 휘발성 액체 B가 녹아 있는 3가지 용액의 증기압을 나타낸 자료이다. 온도 T에서 순수한 증기압 A은 P0이고, 분자량은 X가 B의 2배이다. 온도 T에서, 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, A, B, X는 비전해질이고, 용액은 이상 용액이다.)
⑴ 문제

⑵ 풀이 : ⑤
ㄱ. 용매의 증기압은 용매의 몰분율에 비례하고 nA / (nA + nX) = 4/5이므로, nA / (nA + nX / 2) = 8/9
ㄴ. 세 번째 용액에서 B의 증기압 = 5P0 / 6 - [nA / (nA + nB)] P0 = 5P0 / 6 - [nA / (nA + 2 nX)] P0 = P0 / 6 (단, B의 몰분율은 1 - nA / (nA + 2 nX) = 1/3)이므로, 순수한 B의 증기압은 P0 / 6 × 3 = P0 / 2
ㄷ. PA = 2P0 / 3, PB = P0 / 6이고, 부피, 온도가 일정할 때 몰 수는 압력에 비례하므로 xA, vapor = PA / (PA + PB) = 4/5
9. 다음은 A(g)와 B(g)로부터 C(g)가 생성되는 반응의 열화학 반응식과 압력으로 정의된 평형 상수(Kp)를 나타낸 것이다. 분자량은 B가 A의 5배이다.
aA(g) + bB(g) ⇄ 2C(g), ΔHº, Kp
그림 ㈎는 온도 T1의 강철 용기에 전체 압력이 4 atm인 A(g)와 B(g)의 혼합 기체가 들어 있는 초기 상태를, ㈏는 ㈎로부터 반응이 진행되어 도달한 평형 상태를, ㈐는 ㈏의 온도를 T2로 증가시킨 후, 반응이 진행되어 도달한 평형 상태를 나타낸 것이다. ㈏에서 C(g)의 부분 압력은 PC atm이고, 기체의 전체 압력은 (4 - PC) atm이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 기체는 이상 기체로 거동한다.)
⑴ 문제
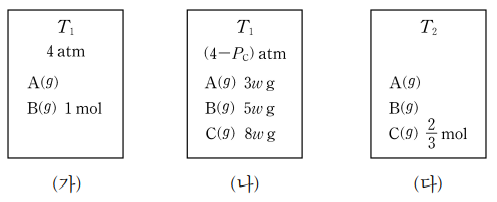

⑵ 풀이 : ④
ㄱ, ㄴ. 온도와 부피가 일정할 때, 몰수는 압력처럼 생각할 수 있다. PA,㈏ + PB,㈏ = 4 - 2PC가 성립하므로 A, B가 합쳐서 2PC만큼 반응하고 동시에 C가 PC만큼 생성되므로 a + b = 4라는 것을 안다. 일반적으로 답은 자연수 혹은 반정수이므로 (a, b) = (1, 3), (2, 2), (3, 1) 중 하나라는 것을 안다. 사실 여기서 (a, b) = (2, 2)가 되면 화학 반응식의 계수가 약분되므로 적절하지 않다는 것을 바로 알 수 있다. 그리고 (a, b) = (3, 1)일 때, A : 6w → 3w, B : 10w → 5w, C : 0w → 8w를 쉽게 찾을 수 있고 모순 없이 잘 성립함을 알 수 있다.
해의 유일성에 대한 논의를 다음과 같이 진행해 보았다.
○ 조건 1. PA,㈎ + PB,㈎ = 4
○ 조건 2. PA,㈏ + PB,㈏ = 4 - 2 × PC,㈏
○ 조건 3. PA,㈏ = 3 × PB,㈏ (∵ B의 분자량 = A의 분자량 × 5)
○ 조건 4. PA,㈎ + 5 × PB,㈎ = 2 × (PB,㈏ + 5 × PB,㈏)
○ 이 밖의 조건은 없는 듯 하고 변수는 총 5개이므로 해를 유일하게 결정할 수 없다. 따라서 a, b가 자연수 혹은 반정수라는 추가적인 가정이 필요하고 정수론적으로 해를 유일하게 결정할 수 있다. 이밖에도 많은 문제가 이러한 가정을 하는 것으로 보인다.
사실 정수해라는 조건이 없으면 답이 여러 개인 문제이다.
○ 예 1
○ A의 분자량 = 1, B의 분자량 = 5, C의 분자량 = 4
○ A의 질량 : ㈎ 6w (3 mol) → ㈏ 3w (1.5 mol)
○ B의 질량 : ㈎ 10w (1 mol) → ㈏ 5w (0.5 mol)
○ C의 질량 : ㈎ 0w (0 mol) → ㈏ 8w (1 mol)
○ 압력 평형상수의 계산
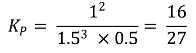
○ 예 2
○ A의 분자량 = 1, B의 분자량 = 5, C의 분자량 = 8
○ A의 질량 : ㈎ 3.5w (1.4 mol) → ㈏ 3w (1.2 mol)
○ B의 질량 : ㈎ 12.5w (1 mol) → ㈏ 5w (0.4 mol)
○ C의 질량 : ㈎ 0w (0 mol) → ㈏ 8w (0.4 mol)
○ 압력 평형상수의 계산
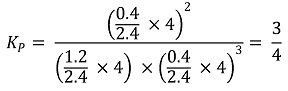
ㄷ. 르 샤틀리에의 원리 : 예 1을 보면, 온도가 증가할 때 C가 감소하므로 ΔHº < 0 (발열반응)
10. 표는 25 ℃에서 Hg (ℓ)과 Hg (g)의 표준 생성 엔탈피(ΔHfº)와 표준 몰 엔트로피(Sº)를 각각 나타낸 것이다. Hg의 정상 끓는점은 600 K이고, 400 K에서 증기압은 P이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 온도에 따른 표준 반응 엔탈피(ΔHº)와 표준 반응 엔트로피(ΔSº)의 변화는 없다.)
⑴ 문제


⑵ 풀이 : ⑤
ㄱ. 600 K에서 정상 (1 atm) 기화 반응은 화학 평형에 있으므로, ΔG = ΔH - TΔS = 60k - 600(a - 75) = 0 ⇔ a = 175
ㄴ. 400 K에서 증기압이 P이므로 압력 P에서 기화 반응은 동적 평형에 있어 계의 자유 에너지는 일정
ㄷ. ΔStot ≥ 0이고 액화하는 계의 ΔSsystem ≤ 0이므로 ΔSsurrounding = ΔStot - ΔSsurrounding ≥ 0이 성립
11. 표는 25 ℃에서 하이드라진(N2H4)과 관련된 반응의 반응식과 표준 반응 엔탈피(ΔHº)를 나타낸 것이다. 25 ℃에서, 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제
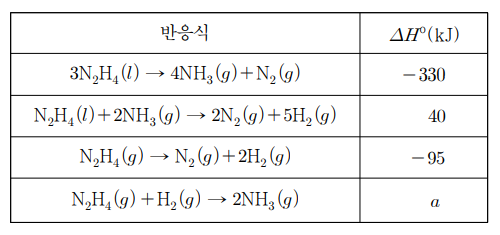

⑵ 풀이 : ①
H2, N2 등 동핵 이원자 기체는 표준 생성 엔탈피를 0으로 정의
4 × ΔHfº (NH3(g)) - 3 × ΔHfº (N2H4(ℓ)) = -330 kJ
-ΔHfº (N2H4(ℓ)) - 2 × ΔHfº (NH3(g)) = 40 kJ
-ΔHfº (N2H4(g)) = -95 kJ
∴ ΔHfº (NH3(g)) = -45 kJ
∴ ΔHfº (N2H4(ℓ)) = 50 kJ
∴ ΔHfº (N2H4(g)) = 95 kJ
ㄱ. N2H4(g)의 표준 생성 엔탈피는 95 kJ/mol
ㄴ. N2H4의 표준 기화 엔탈피는 ΔHfº (N2H4(g)) - ΔHfº (N2H4(ℓ)) = 95 - 50 = 45 kJ/mol
ㄷ. NH3(g)의 표준 생성 엔탈피는 -45 kJ/mol이므로, a = 2 × ΔHfº (NH3(g)) - ΔHfº (N2H4(g)) = -90 - 95 = -185 kJ/mol
12. 표는 25 ℃에서 약산 HA(aq) V0 mL를 NaOH (aq)로 적정하였을 때, 첨가된 NaOH (aq)의 부피에 따른 혼합 용액의 [H+]를 나타낸 것이다. 당량점까지 첨가된 NaOH (aq)의 부피는 Ve mL이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제


⑵ 풀이 : ⑤
ㄱ. 반당량점에서 pH = pKa이므로 Ka = 1.0 × 10-5 (M)
ㄴ. 적정 최초 시점의 데이터로부터 [HA] = 0.2 M인 것을 안다.
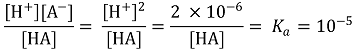
또한, 당량점의 데이터와 NaOH 용액을 2Ve 첨가하였을 때의 데이터로부터 Ve = V임을 안다.
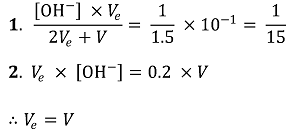
주어진 변수 : V
미지수 : 적정 용액의 [OH-], Ve
필요한 식의 수 : 2
식 1 : 적정 용액을 2Ve 만큼 첨가하였을 때 [H+] = 1.5 × 10-13, 즉 [OH-] = 1/15임을 이용
식 2 : 주어진 용액에서 HA의 몰수 = 당량점까지 첨가한 OH-의 몰수임을 이용
ㄷ. 염기 해리 상수(Kb)의 식으로부터 유도할 수 있다.
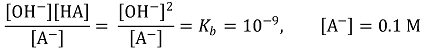
13. 그림은 강철 용기에서 A(g)의 분해 반응이 일어날 때, A(g)의 농도를 시간에 따라 나타낸 것이다. ㈎와 ㈏는 각각 촉매가 없는 경우와 있는 경우이고, 온도는 0 ~ t초 동안 300 K로, t초부터는 330 K로 유지하였다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제
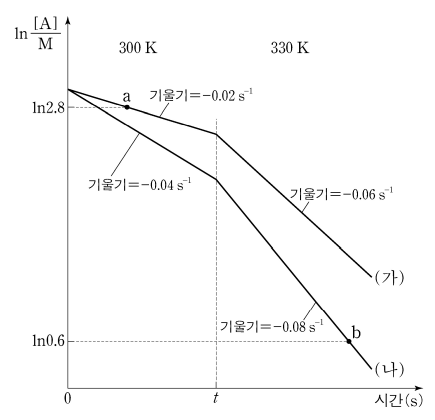

⑵ 풀이 : ③
ㄱ. 주어진 반응과 같은 1차 반응은 ln [A]t = ln [A]0 - kt의 함수식을 따르므로 제시한 설명이 맞다.
ㄴ. 아레니우스식으로부터 활성화 에너지를 구할 수 있음
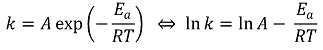
○ k㈎,300K = 0.02 s-1, k㈎,330K = 0.06 s-1
○ ln k㈎,330K - ln k㈎,300K = ln 3 = -[Ea,㈎ / R] (1/330 - 1/300)
○ k㈏,300K = 0.04 s-1, k㈏,330K = 0.08 s-1
○ ln k㈏,330K - ln k㈏,300K = ln 2 = -[Ea,㈏ / R] (1/330 - 1/300)
○ ∴ Ea,㈏ / Ea,㈎ = ln2 / ln3
ㄷ. a에서의 반응속도는 0.02 × 2.8M (M/s)이고 b에서의 반응속도는 0.08 × 0.6M (M/s)으로 a가 b보다 더 큼
14. 다음은 2O3 (g) → 3O2 (g) 반응에 대해 제안된 반응 메커니즘과 이에 근거한 속도 법칙을 나타낸 것이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제
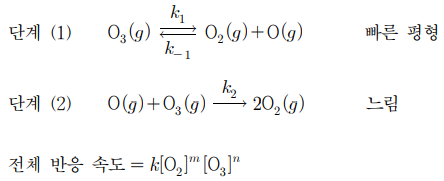

⑵ 풀이 : ②
ㄱ. v(2) (M/s) = k2 [O(g)][O3(g)]이므로 k2의 단위는 s-1M-1
ㄴ, ㄷ. (m+n)은 1이고 k는 제시한 표현이 맞음
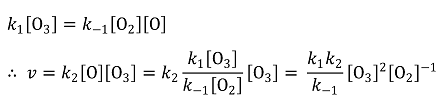
15. 다음은 이산화 황이 물에 녹아 아황산(H2SO3)을 생성하는 반응의 평형 반응식과 25 ℃에서 평형 상수 K이다.
SO2 (g) + H2O (ℓ) ⇄ H2SO3 (aq), K = 1.25
25 ℃에서 이양성자산 H2SO3 (aq)의 단계적 산 해리 상수, Ka1과 Ka2는 각각 1.6 × 10-2과 6.3 × 10-8이다. 25 ℃에서 1.0 atm의 SO2 (g)와 평형을 이루고 있는 수용액에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, √2 = 1.4이다.)
⑴ 문제

⑵ 풀이 : ⑤
ㄱ. [H2SO3] / PSO2 = 1.25, PSO2 = 1 atm이므로 [H2SO3] = 1.25 M
ㄴ. 1단계 산 해리 반응을 이용
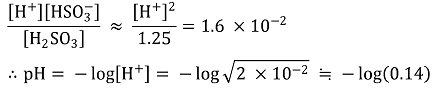
ㄷ. 2단계 산 해리 반응을 이용
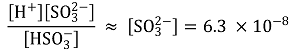
16. 다음은 히스티딘 수용액에서 형성되는 쯔비터 이온(HHis)의 구조와 pH 조건에 따라 생성되는 주된 이온, H3His2+, H2His+, His-을 나타낸 것이다. 25 ℃에서 H3His2+ (aq)의 단계적 산 해리 상수는 Ka1 = 10-1.6, Ka2 = 10-6.0, Ka3 = 10-9.0이다. 25 ℃에서, 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제

⑵ 풀이 : ①
ㄱ. a와 b에서 질소는 각각 sp2 혼성, sp3 혼성. sp 혼성 > sp2 혼성 > sp3 혼성 순으로 전기음성도가 크므로 (혼성효과), sp2 혼성을 가지는 a에 있는 전자가 b보다 더 안정화됨. 따라서 염기도(≒ 불안정성)는 b가 더 커짐
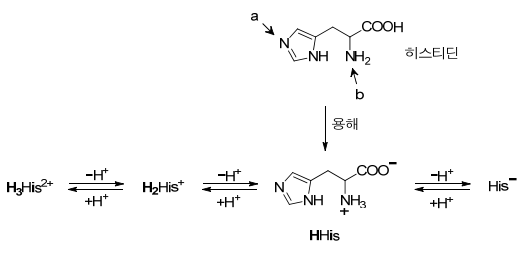
ㄴ. 핸더슨-하셀바흐 방정식에 따르면, pH = 7 = pKa2 + log([HHis] / [H2His+]) = 6 + log 10
ㄷ. 제1 당량점의 pH는 (1.6 + 6.0) / 2 = 3.8
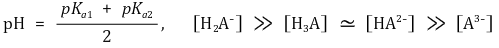
17. 그림은 Ni2O3과 NiO가 입혀진 Ni 전극과 FeO가 입혀진 Fe 전극을 이용하여 만든 갈바니 전지의 초기 상태를 나타낸 것이고, 표는 관련 반쪽 반응의 반응식과 25 ℃에서 표준 환원 전위(Eº)를 나타낸 것이다. 25 ℃에서, 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 주어진 반응 이외의 산화-환원 반응은 일어나지 않는다.)
⑴ 문제

⑵ 풀이 : ③
ㄱ. 전지의 표준 기전력은 0.40 - (-0.87) = 1.27 V
ㄴ. 2개의 전자가 이동할 때, 산화 전극에서는 Fe(s)가 FeO(s)가 되어 산소 원자 1개만큼 무게가 증가하고 환원 전극에서는 Ni2O3(s)가 2NiO(s)가 되어 산소 원자 1개만큼 무게가 감소한다.
ㄷ. 전체 반응식 Fe(s) + Ni2O3(s) → FeO(s) + 2NiO(s)에서 OH-는 반응지수 Q에 영향을 주지 않으므로 KOH의 농도가 기전력에 영향을 주지 않는다.
18. 표는 25 ℃의 수용액에서 산소 화학종이 환원되는 반쪽 반응의 표준 환원 전위(Eº)와 표준 반응 자유 에너지(ΔGº)를 나타낸 것이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은?
⑴ 문제


⑵ 풀이 : ②
ㄱ. ΔGº = -nFEº이므로, a = -4.8 < b = -4.2
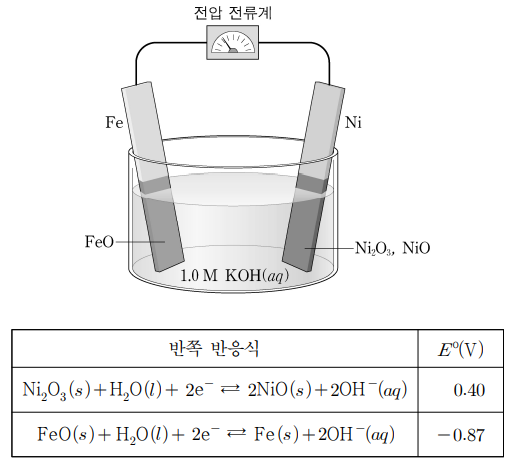
ㄴ. Latimer diagram에 의해, c = (2 × 1.2 + 1 × 2.1) / 3 = 1.5
ㄷ. 반응지수 Q가 작을수록 전위가 높아져 반응이 빠르게 일어나고, [H+]는 반응지수 Q의 식에서 분모에 올 것이므로 [H+]가 높을수록, 즉 pH가 낮을수록 O2(g)의 산화력이 커짐
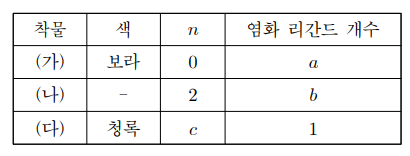
19. 표는 화학식이 CrCl3(H2O)6인 팔면체 Cr 착물 ㈎ ~ ㈐의 색과 화학식당 결정수 개수(n), Cr에 배위 결합된 염화 리간드 개수를 나타낸 것이다. 결정수는 수화된 착물 결정에서 중심 금속에 배위 결합하지 않으면서 구조를 안정화시키는 물(H2O)이다. 이에 대한 설명으로 옳은 것만을 〈보기〉에서 있는 대로 고른 것은? (단, 착물의 색은 Cr의 d 오비탈 사이의 전자 전이에 의한 것이고, 모든 리간드는 한자리 리간드이다.)
⑴ 문제

⑵ 풀이 : ②
ㄱ. 주어진 착물은 팔면체 Cr 착물이므로 배위수는 6이 되어야 한다. 그러므로 n = 염화 리간드 개수가 성립한다. a = 0, b= 2, c = 1이 성립하므로 b는 (a + c)보다 크다. 한편, 배위 결합을 하지 않는 Cl-는 정전기적 인력으로 결합해 있다.
ㄴ. ㈏는 CrCl2(H2O)4로서 다음과 같은 기하 이성질체가 존재한다.
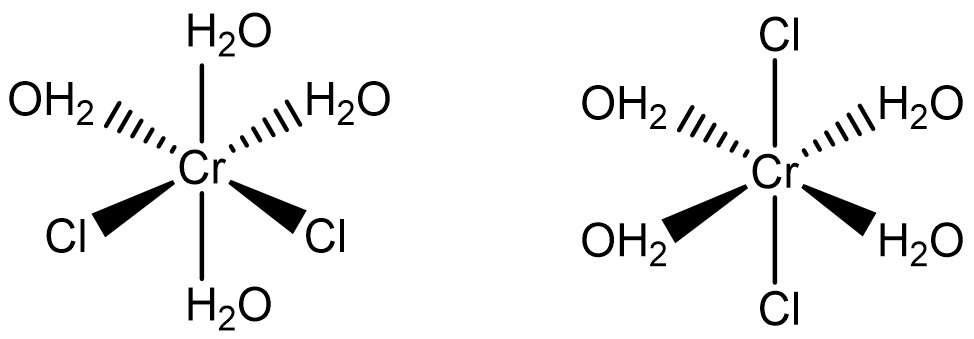
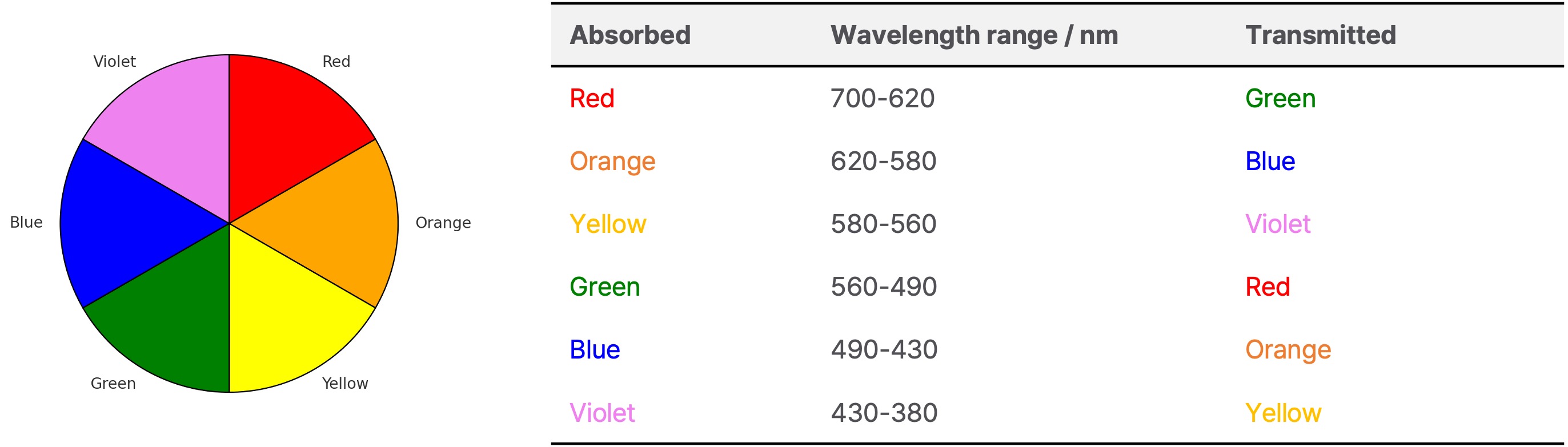
ㄷ. 착물의 색 : 보라색으로 관찰되는 경우가 청록색으로 관찰되는 경우보다 더 흡수 파장이 짧고 결정장 갈라짐(Δ0)이 크다.
20. 다음은 물의 전기 분해를 이용하여 패러데이 상수를 결정하는 실험이다. 이에 대한 설명으로 옳은 것은? (단, 300 K에서 물의 증기압은 27 torr이고 물에 대한 기체의 용해는 무시한다. 기체 상수 R는 0.0821 atm·L/mol·K이고 기체는 이상 기체로 거동한다.)
⑴ 문제


⑵ 풀이 : ⑤
①, ② 2H2O(ℓ) → 2H2(g) + O2(g)로부터 A가 수소 기체가 생성되는 환원 전극, 즉 (-)극이고, B가 산소 기체가 생성되는 산화 전극, 즉 (+)극이라는 사실을 알 수 있다.
③ 전기 분해 반응에 이용되는 OH-이 촉매처럼 이용되므로 (즉, pH가 일정하므로) 직류 전원 장치의 전압은 일정하게 유지된다. 혹은 전기 분해 반응에서 기체 생성물로 인해 과전위(overpotential)를 필요로 하는 것처럼, 산소 및 수소 기체 생성물로 인해 직류 전원 장치가 계에 인가해야 하는 전압이 증가해야 할 수 있다.
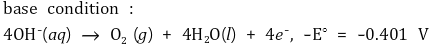
④ 단위 시간당 이동하는 전하의 양인 전류를 일정하게 제공하고 (이유 1), OH-는 반응 중에 일정하게 유지되므로 (이유 2) 시간은 변하지 않는다.
⑤ 전자의 몰수 = 2 × 1 × V / (0.0821 × 300) = 0.2 × t / F (단, F는 패러데이 상수로서 1 F는 1몰 전자의 전하량을 의미)
입력: 2022.09.29 09:59