벡터의 내적 공식 증명
추천글 : 【수학】 수학 목차
Q.
3차원 벡터 v1, v2에 대해 다음 내적 공식이 성립함을 증명하여라.
v1 · v2 = |v1| |v2| cos θ12
단, (·)는 내적 연산이고, θ12는 두 벡터의 사잇각이다.
Solution.
일단 증명을 위한 전략은 이렇다; 우선 벡터의 내적이 회전변환에 대해 보존되는 '물리적인' 양임을 증명한다. (물리적인 양의 예에는 길이와 넓이 등이 있다.) 그러면 증명하기 편리한 2D의 경우로 간주해도 무방함을 보일 수 있고, 정말로 2D에서 해당 공식이 성립함을 보임으로써 주어진 lemma를 보인다.
이제 회전에 대한 보존성을 증명하기 위해 z축에 대한 회전을 고려한다. z 축의 양의 방향을 엄지로 가리킬 때 오른나사로 θ만큼 회전하는 회전변환은 다음과 같이 표현할 수 있다.

따라서 A = (a1, a2, a3), B = (b1, b2, b3)의 변환 A' = (a1', a2', a3'), B' = (b1', b2', b3')은 다음과 같다.

이때 내적을 하면 다음과 같은 관계식을 얻을 수 있다.

따라서 z축에 대한 회전변환에 대한 보존법칙이 성립한다. 대칭성에 의해 z축뿐만 아니라 x축, y축에서도 회전변환에 대한 보존법칙이 성립할 것임을 단언할 수 있다. 따라서 벡터의 내적은 임의의 회전에 대해 보존된다.벡터의 내적이 회전에 대해 보존된다는 사실이 중요한 까닭은 두 벡터의 사잇각도 회전에 대해 보존되기 때문이다. 그러므로 x-y 평면 상에 있는 임의의 두 벡터가 주어진 lemma를 만족함을 증명할 수 있으면, 3차원 상에서도 그 lemma가 성립한다.
이제 x-y 평면 상에 있는 임의의 두 벡터 w1, w2를 고려하자. 그러면 벡터의 내적은 다음과 같이 표현된다.
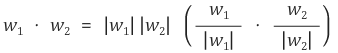
이제 x-y 평면 상에 있는 임의의 두 단위벡터의 내적이 사잇각의 cos 값임을 보이면 충분하다. 그런데 이는 쉽게 증명할 수 있다.
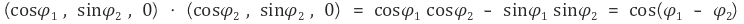
따라서 벡터의 내적 공식을 증명하였다.
입력: 2015.12.05 09:26
수정: 2016.06.27 03:24
'▶ 자연과학 > ▷ 기하학' 카테고리의 다른 글
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2005년 ~ 2009년) (0) | 2024.05.05 |
|---|---|
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2000년 ~ 2004년) (0) | 2024.05.05 |
| 【기하학】 기하 기초 문제 (01~20) (0) | 2022.05.20 |
| 【기하학】 축구공과 오일러 법칙 (0) | 2019.11.05 |
| 【국제수학올림피아드】 IMO 기하 문제 풀이 종합 (0) | 2016.06.23 |




최근댓글