제 42회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 42회 전국 대학생 수학경시대회
제 2 분야
2024년 11월 2일 (10:30 - 13:00)
1. 다음 행렬 A에 대하여 등식 A5 = aA2 + bA + cI가 성립하도록 하는 실수 a, b, c를 구하여라. (단, I는 3 × 3 단위행렬)

Solution.
다음 식을 발견할 수 있다.

∴ A5 = A2 × (-3A) = (-3)2 A이므로 a = 0, b = 9, c = 0
참고로, 공식 풀이에서는 대응되는 문제가 아닌 제1분야 2번 문제 풀이를 제시하고 있으므로 유의해야 한다.
2. 다음 미분방정식의 해 y(x)를 구하여라.

Solution.
u = x - 1, v = y - x라고 두면 다음을 얻을 수 있다.

3. 양수 a에 대하여 3차원 공간의 입체 V를 다음과 같이 정의하자. 입체 V의 부피가 7π / 12일 때 a의 값을 구하여라.
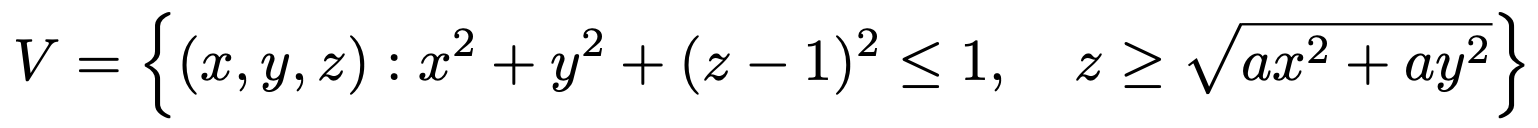
Solution.
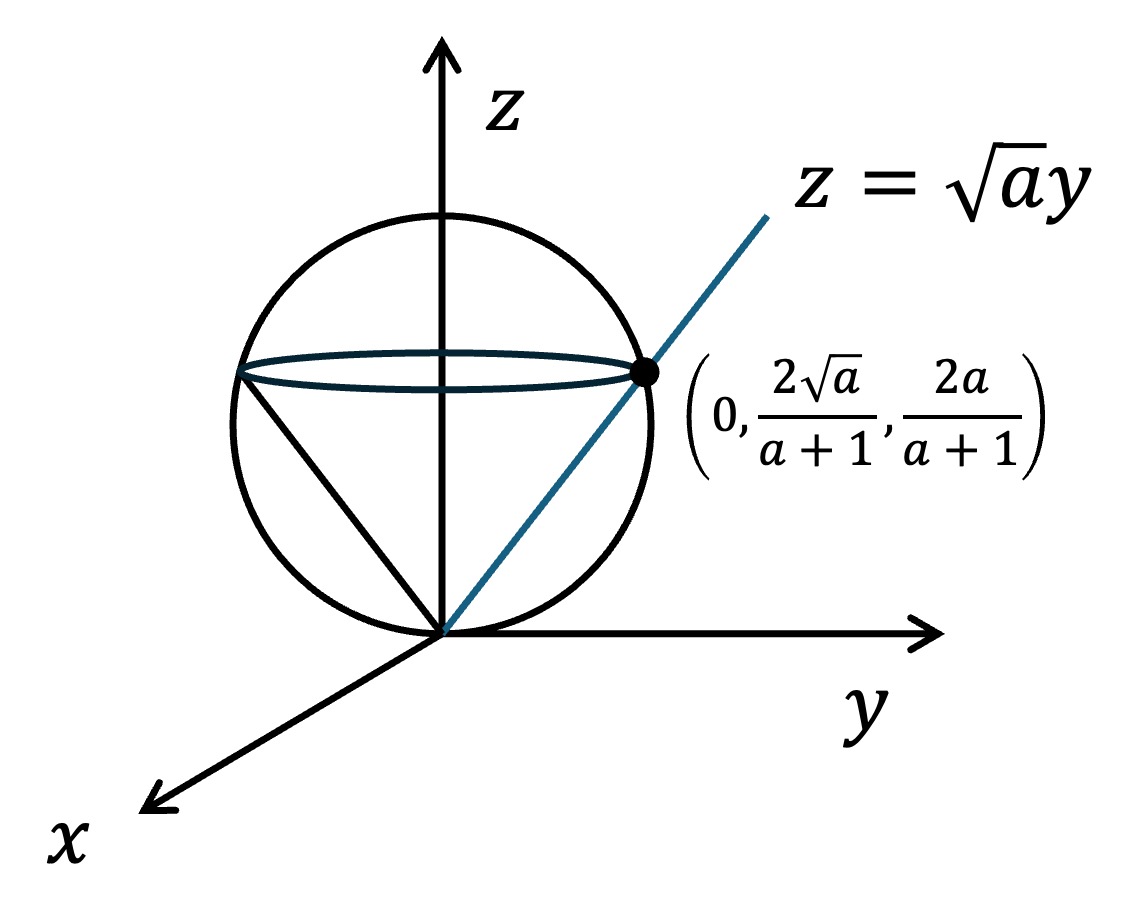
x2 + y2 + (z-1)2 = 1과 z = √a y의 교점은 (0, 2√a / (a + 1), 2a / (a+1))이다.
○ 영역 1의 부피
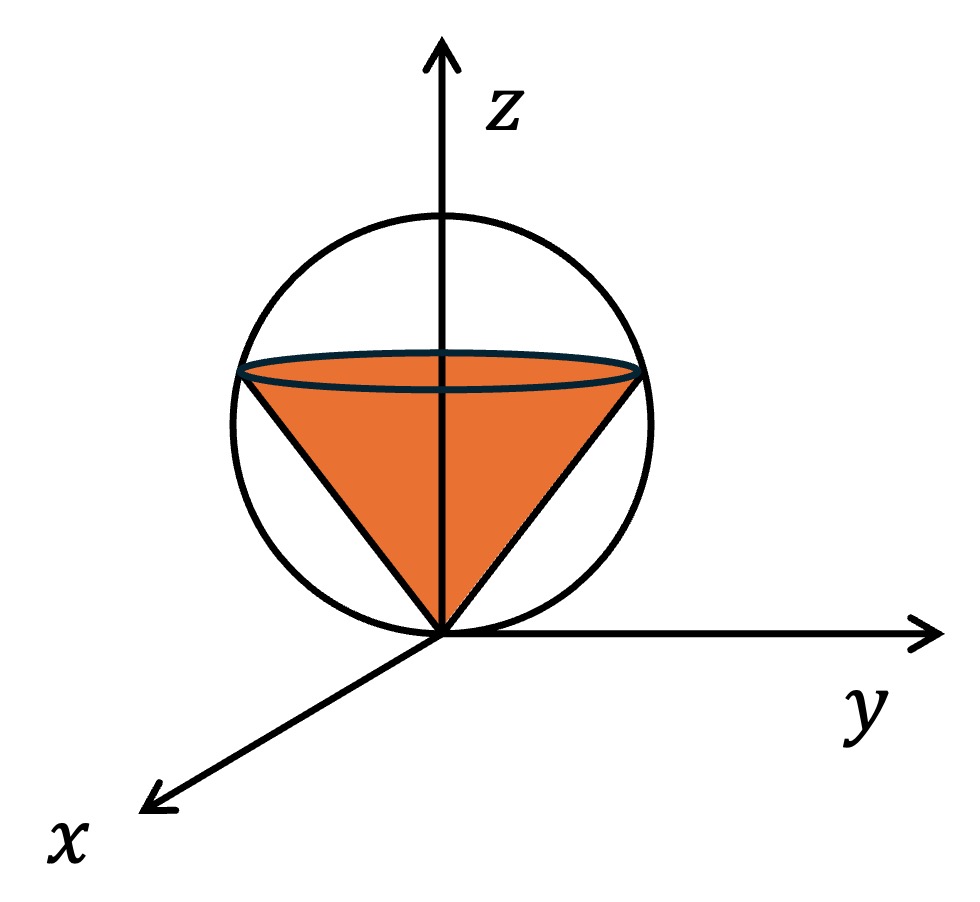
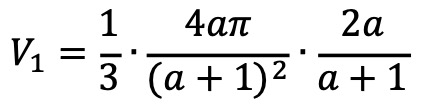
○ 영역 2의 부피
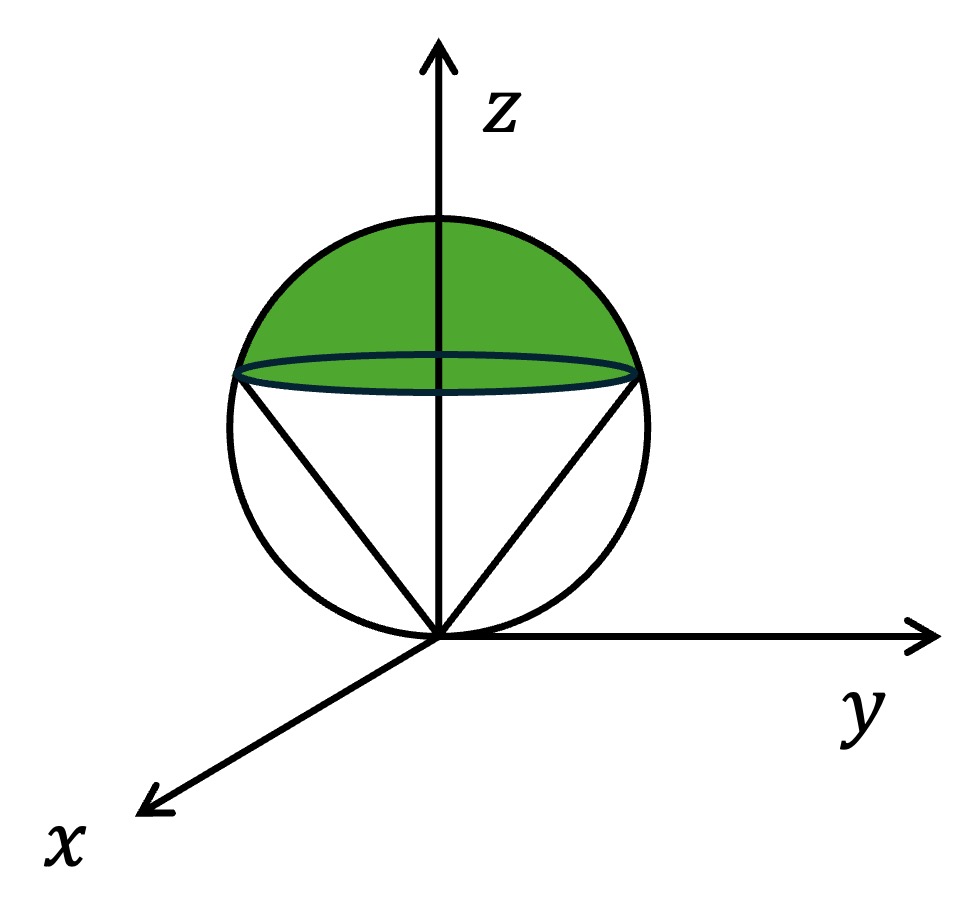
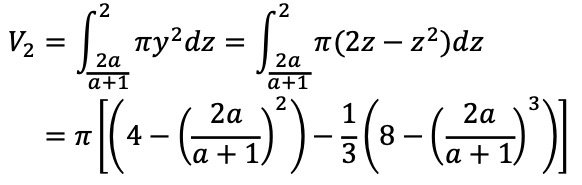
V = V1 + V2 = 7π / 12로부터, a = 3을 얻을 수 있다. (ref)
4. 다음 식을 만족하는 실수 N을 구하여라.
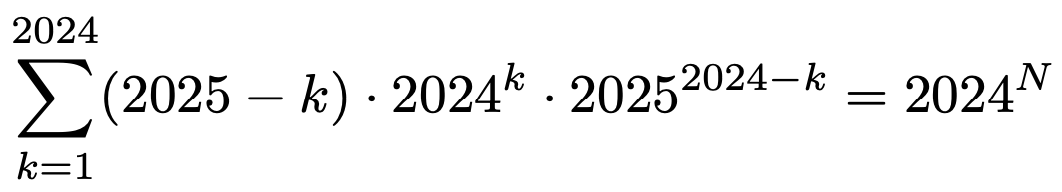
Solution.

5. 다음 이상적분(improper integral)의 값을 구하여라.
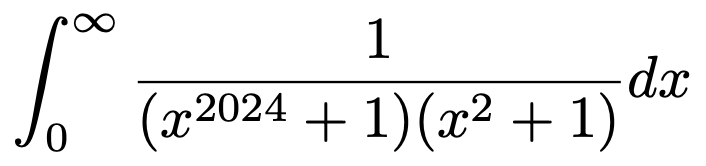
Solution.
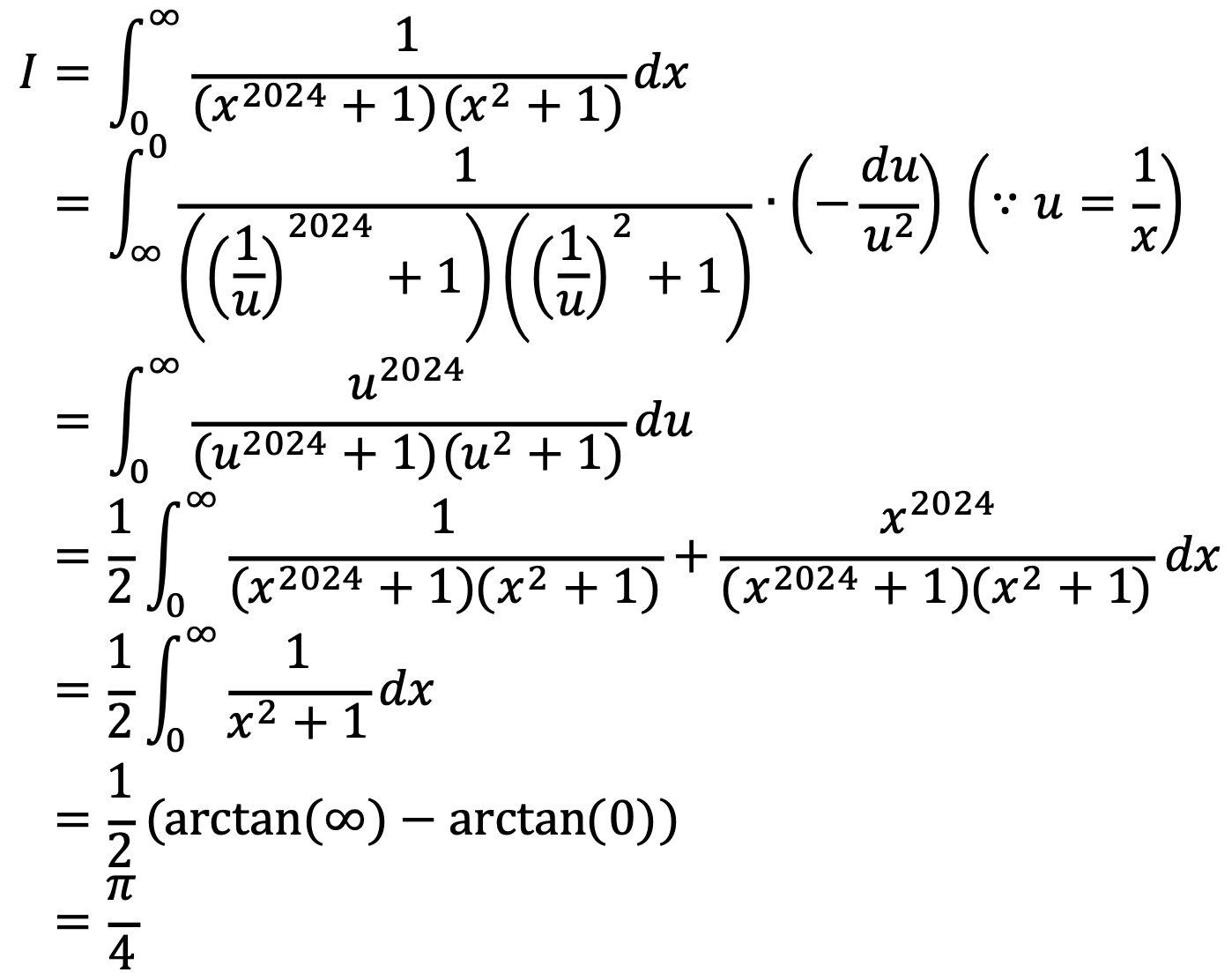
6. 크기가 n × n인 실행렬 A, B에 대하여 rank(B) = 1일 때 다음 부등식을 증명하여라. (단, n ≥ 2)
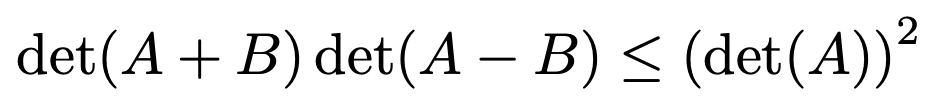
Solution.
rank(B) = 1이므로 B는 적당한 n × 1 실수 열벡터 u, v에 대하여 B = uvT로 나타낼 수 있다.
행렬식과 관련하여 다음 성질이 만족함을 주목하자.
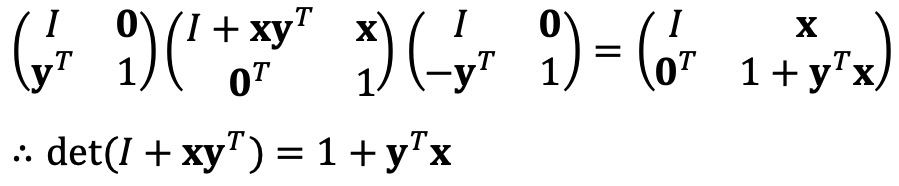
따라서 다음과 같이 (준식)을 보일 수 있다.
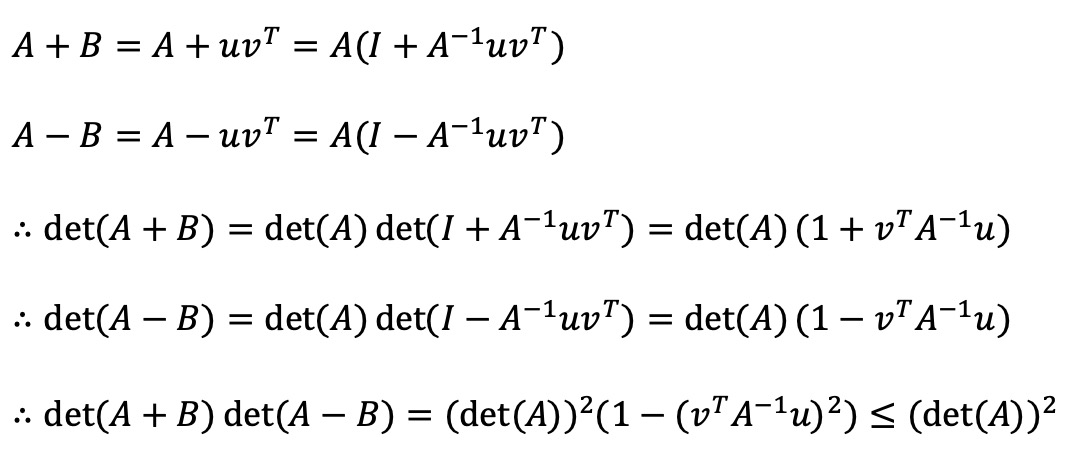
7. 2차원 좌표평면 위의 유한한 닫힌 블록 영역 D에 대하여 D의 경계 β가 다음을 만족한다고 하자.
⑴ β는 매끄러운 단순폐곡선이다.
⑵ β 위의 임의의 점 O에 대하여 O를 중심으로 하는 반지름이 1인 원은 β와 두 점에서만 만난다.
⑶ β 위의 임의의 점 O에서 그린 접선은 O를 제외한 다른 점에서 β와 만나지 않는다.
길이가 1인 막대 PQ의 중점을 M이라 하자. 막대의 양 끝점 P, Q가 항상 β 위에 놓이도록 막대를 한 바퀴 돌리면(즉, 곡선 β를 따라 두 점 P, Q를 연속적으로 한 바퀴 돌리면) M의 자취가 단순폐곡선 γ가 된다고 하자. 이때 두 곡선 β와 γ 사이에 있는 영역의 넓이가 π/4임을 보여라.
Solution.

위와 같은 삼각형이 주어져 있을 때, 파푸스의 중선정리에 따르면 a2 + b2 = 2(c2 + d2)이 성립한다.
그러므로 다음이 성립한다.


입력: 2024.12.07 19:01
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2024.12.29 |
|---|---|
| 【대수경】 제 38회 전국 대학생 수학 경시대회 제 1 분야 (2) | 2024.12.29 |
| 【대수경】 제 42회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.12.07 |
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 2 분야 (4) | 2024.12.06 |
| 【대수경】 제 39회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2024.10.04 |




최근댓글