신념의 힘
추천글 : 【집단행동과학】 집단행동과학 목차
a. 행렬의 대각화
b. Markov chain
c. 그래프 이론
Reynolds 박사는 집단행동에는 세 가지 규칙이 있다고 말했다.
1) 분리 : 지나치게 모여 있는 곳은 피한다. (short range repulsion)
2) 정렬 : 인접한 개체들의 평균 방향을 응시한다.
3) 응집 : 인접한 개체들의 평균 위치로 이동한다. (long range attraction)
요약하면, 사람, 새, 물고기 등의 개체는 주위의 개체에 영향을 받아 평균적으로 행동하되, 그들과 적당 거리를 유지한다.
이 포스팅에서는 어떤 집단 내에 자신의 신념대로만 살아가는 개체가 단 하나 있을 때, 충분한 시간이 지나면 집단 내 모든 개체의 신념이 그 개체와 같은 신념을 가지게 된다는 것을 증명하고자 한다. 단 다소 추상적일 수 있는 개념인 '신념'을 보다 구체화하기 위해 화살표의 방향으로 나타내려고 한다. 그런데 모든 집단에서 그런 현상이 일어나는 것은 아니다. 가령, 자신의 신념대로만 살아가는 개체가 모집단에서 아주 멀리 떨어져 다른 개체와 상호작용을 할 수 없을 때가 있을 수 있다. 따라서 모든 개체가 어떤 순간에도 주위에 하나 이상의 이웃 개체가 존재해야 하며, 이를 연결성(to be jointly connected)이라고 정의한다. 그리고 이러한 성질은 수학적으로 정의할 수 있다. (ref) 인간은 끊임없이 다른 사람들과 상호작용하고, 또 그래야 하는 동물이므로 인간 집단에서의 연결성은 당연해 보인다.
i 번째 입자의 이웃의 집합 Ni(t)를 시간 t에서 i 번째 입자와 반경 r 이내에 있는 입자들의 집합으로 정의하자. 단, 시간 t는 음이 아닌 정수이고 자기 자신은 이웃에 포함시키지 않는다. 또한 θi(t)를 시간 t에서 [0, 2π)의 구간에 놓이는, 방향을 나타내는 값으로 정의하자. 그러면, 규칙 2)에 의해 다음 식을 찾을 수 있다.
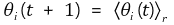
i 번째 입자의 t + 1번째 방향은 i 번째 입자의 이웃과 자신의 방향의 평균값이다. ni(t)를 Ni(t)의 원소 개수라고 정의할 때, 〈θi(t)〉r 은 다음과 같이 나타난다.
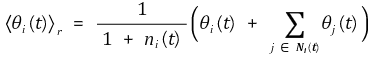
위 식을 행렬로 나타내기 위해 몇 가지 정의를 하자. 우선 Ƥ의 부분집합인 p = {1, 2, … , n}를 꼭짓점으로 하고, 만약 i번째 입자와 j번째 입자가 이웃 관계라면 선분 (i, j)가 그려져 있는 그래프를 ₲p라고 정의하자. (단, 그래프는 시간에 따라 계속 변한다는 사실에 주의한다.) 또한 i 행, i 열이 ni(t)인 대각행렬을 Dp라고 정의하자. 마지막으로 i 번째 입자와 j 번째 입자 간 이웃관계의 여부와 i 행 j 열의 성분과 대응되는 인접행렬(adjacency matrix)을 Ap이라고 정의하자. (참고로, 인접행렬은 Markov chain과 관련이 있다.) 단, Dp와 Ap는 그래프 ₲p에 대한 행렬이다. 이러한 정의를 바탕으로 다음 식을 얻을 수 있다.
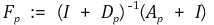
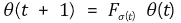
이때 θ는 열 벡터이고 σ(t)는 시간 t와 그래프 ₲를 대응시키는 함수(즉, 사상)이다. 그런데 σ는 시스템의 전반적인 특성을 나타내는 인자로 시뮬레이션을 통한 추이 분석은 비교적 용이하나, 수렴성을 연구하기에는 다소 어려움이 있다. 따라서 초등적인 증명은 어려워 보인다.
대각행렬의 역행렬은 각 대각선 성분들을 역수로 취해 주면 된다. 따라서 정의한 바에 따르면 Fp는 정사각행렬이고, 모든 성분이 음이 아니다. 또한 직관적으로 Fp1 = 1이 성립함을 알 수 있다. (단, 1은 n 개의 원소를 가진 열벡터이다.) 이러한 성질들을 만족하는 행렬을 stochastic하다고 말한다. (즉, 행렬의 고유치 중 1이 있는 경우) 또한 정사각행렬이고, 모든 성분이 음이 아니며, 어떤 m ≥ 1에 대하여 Mm의 모든 성분이 양수가 되는 m이 존재하는 행렬 M을 primitive하다고 말한다. 연결성이 보장돼 있는 (Ap + I)는 primitive한데, 이는 수학적 귀납법으로 증명 가능하다. (I + Dp)-1는 대각행렬이고, 대각행렬과 어떤 행렬의 곱은 교환법칙이 가능하므로 Fp도 또한 primitive하다. 만약 어떤 n × n 행렬이 primitive하면, 모든 성분이 양수인 고유벡터는 절대값이 가장 큰 고유값과 대응되고, 나머지 n-1개의 고유값의 절대값이 그 고유값보다 작다는 것이 알려져 있다. (ref) 따라서 stochastic하고, primitive한 행렬은 값이 1인 고유값 1개를 가지고, 나머지 n - 1개의 고유값은 구간 (-1, 1)의 원소가 되는데, 이러한 행렬을 ergodic하다고 한다.
Figure. 1. 에르고딕 시스템과 비에르고딕 시스템
1) 에르고딕 시스템(ergodic system) : 시간이 지남에 따라 시스템이 여러 상태를 골고루 거치며, 시간 평균이 공간 평균과 동일한 경우
2) 비에르고딕 시스템(non-ergodic system) : 시간이 지나도 특정 상태에만 머물러 있거나, 시간에 따른 평균이 집단 평균과 다를 수 있는 경우
열 벡터로 표현된 i 번째 고유벡터를 vi, 그에 대응하는 고유벡터를 λi라고 할 때 ergodic한 행렬은 다음과 같은 성질을 갖는다.
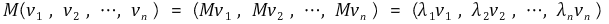
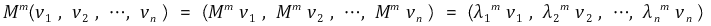
이때, c는 행 벡터이다. 이제 Wolfowitz's theorem을 소개한다. 유한집합 {M1, M2, … , Mm}에서 중복을 허용하여 임의로 뽑은 Mi(k)에 대하여 Mi(1)×Mi(2)× … ×Mi(j), j < ∞가 항상 ergodic하다고 하자. 이때 다음이 성립한다.
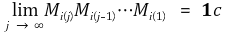
모든 형태의 I + Ap를 표현할 수 있는 유한집합 {I + Ap(1), I + Ap(2), … , I + Ap(m)}을 찾을 수 있단 사실은 당연하다. 그런데 그 집합에서 중복을 허용하여 임의로 뽑은 I + Ap(k)에 대하여 (I + Ap(1))×(I + Ap(2))× … ×(I + Ap(j)), j < ∞가 항상 primitive함은 쉽게 확인할 수 있다. 한편, I + Ap와 똑같은 수만큼 존재하는 모든 형태의 Fp를 표현할 수 있는 유한집합 {Fp(1), Fp(2), … , Fp(m)}을 찾을 수 있단 사실도 당연하다. 그런데 임의로 뽑은 Fp(k)에 대한 Fp(1)×Fp(2)× … ×Fp(j), j < ∞는 적당한 대각행렬과 primitive한 행렬의 곱이므로 이도 또한 primitive하다. 그런데 임의로 뽑은 F p(k)에 대한 Fp(1)×Fp(2)× … ×Fp(j), j < ∞는 아주 쉽게 stochastic함을 확인할 수 있다. 그러므로 ergodic하다. 따라서 Wolfowitz's theorem에 의해 다음이 성립한다.
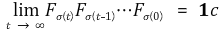
이때 p를 시간에 대한 함수로 나타내기 위해 σ(t)로 표시했다. 이때 θ(t)의 점화식을 이용하면 θ(t)가 수렴하는 벡터를 찾을 수 있다.
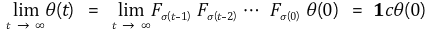
그런데 열 벡터 1cθ(0)는 모든 성분의 값이 같다. 따라서 모든 개체의 신념이 수렴했음을 확인하였다. 만약 집단 내에 신념이 절대로 변하지 않는 단 하나의 개체가 있다면 어떨까? 위의 증명은 Reynolds가 제시한 모델보다 더 포괄적이어서 그 상황에 대해서도 동일한 결론을 적용할 수 있다. 즉, 어쨌든 모든 개체의 신념은 수렴해야 한다. 따라서 당연히 그 하나의 개체가 가지고 있는 신념대로 모두가 바뀔 것이다. 예로부터 신념이 강한 사람이 줄곧 세상을 (좋든 나쁘든) 바꾸곤 했는데, 이러한 사람들은 자신이 속한 집단에 동화하려는 인간의 기본적인 속성을 극복한 사람이라고 할 수 있겠다. 세상을 바꾸고 싶은가? 그렇다면 절대로 휘둘리지 않는 강한 신념을 가져라!
입력: 2016.06.30 17:36
수정: 2024.10.03 09:58
'▶ 사회과학 > ▷ 집단행동과학' 카테고리의 다른 글
| 【집단행동과학】 집단지성이란, 그리고 고등인지란 (0) | 2023.04.17 |
|---|---|
| 【집단행동과학】 대중의 지혜 (0) | 2019.07.04 |
| 【집단행동과학】 계산, 그것은 생각한다는 것을 말하는 것인가? (0) | 2016.06.22 |
| 【집단행동과학】 집단행동과학 목차 (0) | 2016.06.21 |
최근댓글