축구공과 오일러 법칙
추천글 : 【기하학】 기하학 목차
1. 정의 [본문]
2. 오일러의 법칙 적용 [본문]
3. 추가적인 정보 이용 [본문]
1. 정의 [목차]
⑴ A : 오각형의 개수
⑵ B : 육각형의 개수
2. 오일러의 법칙 적용 [목차]
⑴ 꼭짓점(vertex)의 수 V, 모서리(edge)의 수 E, 면(facet)의 수 F에 대해 다음이 성립

⑵ 꼭짓점의 수의 관계식 : 한 꼭짓점에 세 개의 면이 만난다는 사실을 이용

⑶ 모서리의 수의 관계식 : 한 모서리에 두 개의 면이 만난다는 사실을 이용

⑷ 면의 수의 관계식

⑸ 오일러의 법칙 적용
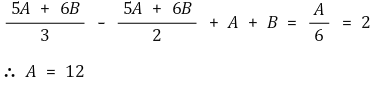
3. 추가적인 정보 이용 [목차]
⑴ 추가적인 정보
① 임의의 육각형의 세 변에는 육각형이, 나머지 세 변에는 오각형이 맞닿아 있음
② 임의의 오각형의 모든 변에는 육각형이 맞닿아 있음
⑵ 계산 전략
① (중복을 허용하여) 육각형의 관점에서 센 오각형의 수 ÷ 중복수 = 오각형의 개수 = 12
② 중복수 = 5 (∵ 오각형의 관점에서 인접한 다섯 개의 육각형으로부터 한 번씩 세어졌으므로)
③ 계산과정
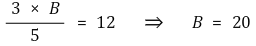
입력: 2019.11.05 19:03
'▶ 자연과학 > ▷ 기하학' 카테고리의 다른 글
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2000년 ~ 2004년) (0) | 2024.05.05 |
|---|---|
| 【기하학】 기하 기초 문제 [01~20] (0) | 2022.05.20 |
| 【기하학】 벡터의 내적 공식 증명 (0) | 2016.06.27 |
| 【기하학】 기하학 목차 (0) | 2016.06.25 |
| 【기하학】 대수경 중 기하 문제 모음 (0) | 2016.06.25 |





최근댓글