2018 국가공무원 5급(기술) 제3문
추천글 : 【공업화학】 공업화학 목차
a. 반응속도론
Q. 고분자 중합반응의 속도와 관련하여 다음 물음에 답하시오.
Q1. 아디프산(adipic acid)과 1,10-데칸다이올(1,10-decanediol)의 폴리에스테르화 반응에 있어서 별도의 촉매를 사용하지 않는 경우, k[COOH]3으로 표현될 수 있다. 이때 반응시간(t)과 카르복실기의 전환율(P) 사이의 관계식을 유도하고, 전환율이 0.99가 되기 위한 반응시간과 전환율이 0.90이 되기 위한 반응시간의 비율(t0.99 / t0.90)을 구하시오. (단, k는 반응의 속도상수이고, [COOH]는 아디프산 카르복실기의 농도이다.)
A1.



전환율이 0.99일 때 [COOH]t = 0.01 [COOH]0이고, 0.90일 때 [COOH]t = 0.10 [COOH]0이다.
그러므로 다음과 같다.
2kt0.99 = 9999 / [COOH]02
2kt0.90 = 99 / [COOH]02
∴ t0.99 / t0.90 = 101
Q2. 원자-이동 라디칼 중합(ATRP, atom transfer radical polymerization)은 중합과정 동안 성장라디칼이 거의 소멸되지 않는 리빙(living) 특성을 지닌 고분자 중합 방법으로, 1에 가까운 다분산지수(PDI)를 얻을 수 있는 것이 특징이다. 단량체의 초기 농도를 [M]0라고 하고 특정 반응시간(t)에서의 단량체 농도를 [M]이라고 할 때, ln([M]0 / [M]) 값을 반응시간에 따라 도시하였을 경우 원점을 지나는 직선에 가까운 형태가 나오는 이유를 동역학적으로 설명하시오. 또한 다분산지수가 1에 가까운 값이 나오는 이유를 설명하시오.
A2.
다음은 평균 분자량의 종류이다.
○ 수 평균 분자량(Mn) : 어는점 내림, 끓는점 오름, 증기압 내림, 삼투압 등과 관련

○ 중량 평균 분자량(Mw) : 점도, 인장력 등과 관련
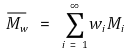
○ Z 평균 분자량(Mz) : melt elasticity 등과 관련
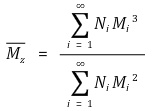
○ 점도 평균 분자량(Mv) : 점도 평균 분자량
○ Mz > Mw > Mv > Mn
○ 다분산지수(PDI, polydispersity index)
○ 정의 : PDI = Mw ÷ Mn
○ 배경이론
○ 고분자의 경우 단량체의 개수에 따라 여러 종류의 분자량이 가능
○ molecular weight - relative fraction 그래프는 narrow distribution, broad distribution, bimodal distribution 등으로 분류
○ bimodal distribution : 2가지 다른 환경으로부터 고분자가 중합될 때 보이는 분포
○ 분자량 분포가 좁을수록 Mw와 Mn이 가까워짐
○ 단분산, 다분산
○ 단분산(monodisperse) : PDI = 1
○ 다분산(polydisperse) : PDI > 1
다음은 일반적인 원자-이동 라디칼 중합반응의 메커니즘이다.

Figure. 1. 일반적인 원자-이동 라디칼 중합반응의 메커니즘
다음은 원자-이동 라디칼 중합반응의 예이다.

원자-이동 라디칼 중합반응은 개시 과정에서 휴면상태(dormant)에 있는 분자를 활성화시킨다.
하지만 그 과정은 역반응이 우세하기 때문에 기존 중합체에 단량체가 하나만 붙자마자 다시 비활성화된다.
따라서 단량체 각각을 붙여 나가는 매 중합과정이 엄격하게 조절될 수 있다.
그러므로 모든 중합체가 동일한 분자량을 가질 수 있게 되어 PDI = 1이다.
또한 매 단계에서 단량체 여러 개가 한꺼번에 반응에 참가하지 못하고 딱 한 개만 반응한다는 점을 상기하자.
동역학적으로 단량체의 농도가 2배, 3배가 되면 반응속도도 2배, 3배가 된다는 것을 알 수 있다.
따라서 원자-이동 라디칼 중합반응은 1차 반응이다.
1차 반응은 ln [A]t = ln [A]0 - kt와 같은 함수를 따르므로 ln([M]0/M)은 원점을 지나고 기울기가 k인 직선 그래프를 그린다.
위와 같이 원자-이동 라디칼 중합반응은 분명 굉장히 순도 높은 중합체를 얻을 수 있는 유용한 반응이다.
하지만 그만큼 촉매가 많이 사용되기 때문에 비싼 반응일 수밖에 없다.
최근에는 이 반응을 보다 저렴하게 수행할 수 있는 여러 가지 시도가 이뤄지고 있다.
입력 : 2019.05.13 22:04
'▶ 자연과학 > ▷ 5급 기술고시 풀이' 카테고리의 다른 글
| 【공업화학】 2017 국가공무원 5급(기술) 제2문 (0) | 2019.05.18 |
|---|---|
| 【공업화학】 2018 국가공무원 5급(기술) 제4문 (0) | 2019.05.13 |
| 【공업화학】 2018 국가공무원 5급(기술) 제2문 (0) | 2019.05.13 |
| 【공업화학】 2018 국가공무원 5급(기술) 제1문 (0) | 2019.05.13 |
| 【환경화학】 2010 국가공무원 5급(기술) 제4문 (0) | 2019.04.04 |



최근댓글