2-1강. 쌍성계의 공전면이 한 평면임을 증명
추천글 : 【지구과학】 2강. 태양계
1. 문제 [본문]
2. 가정 [본문]
3. 풀이 [본문]
a. 케플러 법칙 증명
1. 문제 [목차]
쌍성계의 궤도면은 한 평면일까? 쌍성계의 평면은 케플러 법칙으로 기술될 수 있기 때문에 태양 주위를 행성이 도는 태양계의 궤도면이 한 평면임을 증명하면 쌍성계의 궤도면이 한 평면임을 확인할 수 있다. 그리하여 태양계의 궤도면이 한 평면임을 아래와 같이 증명한다.
2. 가정 [목차]
태양이 공간 R3의 원점에 있고 한 행성이 태양을 돌고 있다고 하자. 이때 행성의 시간 t에서의 위치를 r = r(t)로 나타내자. 여기서 r = r(t)은 C2 함수이고 (즉, 2차 미분계수가 존재) 다음을 가정한다: 아래에서 G는 만유인력 상수, m은 행성의 질량, M은 태양의 질량이다.
Ⅰ. 모든 t에 대해 다음이 성립한다. 단, r(t) = | r(t) |이다.

Ⅱ. 양수 α, β가 있어 모든 t에 대해 α < r(t) < β이다. 즉, r(t)는 임의의 구간에 대해 유계이다.
Ⅲ. 행성은 한 선이나 원 위에서 움직이지 않는다. 이는 관측 사실에 근거한다.
3. 풀이 [목차]
우선 다음이 성립한다.

여기서 Ⅰ로부터 r''(t)와 r(t)가 평행함을 이용하였다. 따라서 c = r(0) × r'(0)라 하면 모든 t에 대해 c = r(t) × r'(t)이고 c가 r(t)와 수직임을 안다. 따라서 π를 원점을 지나 c와 수직인 평면이라고 하면 r(t)는 항상 π 위에 있다. 이때 c ≠ O임을 확인하자. c = O이라고 하면, r(t), r'(t)가 평행이니 f(t) ∈ R가 있어 r'(t) = f(t) r(t)가 성립한다. F(t)를 다음과 같이 정의하자.

그러면 가정 Ⅲ과 모순되는 결론이 나온다.
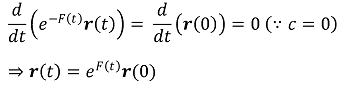
입력 : 2022.09.03 01:50
'▶ 자연과학 > ▷ 지구과학' 카테고리의 다른 글
| 【지구과학】 4-2강. 성운에서 별이 형성되는 시간 구하기 (0) | 2022.09.03 |
|---|---|
| 【지구과학】 4-1강. 우주 산업 (0) | 2022.08.28 |
| 【지구과학】 지구과학 목차 (0) | 2020.01.12 |
| 【지구과학】 16강. 지구온난화 (0) | 2019.08.16 |
| 【지구과학】 15강. 지구의 역사 (0) | 2019.08.16 |




최근댓글