4-2강. 성운에서 별이 형성되는 시간 구하기
추천글 : 【지구과학】 4강. 우주
1. 문제 [본문]
2. 첫 번째 풀이 [본문]
3. 두 번째 풀이 [본문]

1. 문제 [목차]
기체 구의 온도가 매우 낮아 (약 10 K) 기체 운동을 무시할 수 있다고 할 때, 기체 구가 응축하여 한 점이 되는 데 걸리는 시간을 구하여라. 단, 회전, 온도, 자기장, 기체 압력 등은 고려하지 않는다.
2. 첫 번째 풀이 [목차]
이 문제를 푸는 데 있어 기체 구 표면의 입자가 매우 길쭉한 타원 궤도의 원일점에 있는 행성의 처지와 유사하다는 관점 하에 케플러 법칙을 적용하여 푼 바 있다.

케플러는 질량이 M인 천체 주위를 도는 질량 m인 천체가 있다고 할 때, 질량 m인 천체가 그리는 타원 궤도의 장반경 a, 주기 T에 대해 다음과 같은 조화의 법칙이 성립한다고 발표했다.
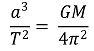
따라서 장반경 a = R / 2 (단, R은 주어진 기체 구의 반지름), 주어진 기체 구의 밀도를 ρ로 두면,
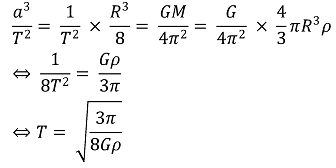
우선 위 식은 타원의 단반경을 모르기 때문에 M을 구할 때 논리적 비약이 있음을 미리 밝혀둔다. 그런데 질량 m인 천체가 그린 궤적은 전체의 반이기 때문에 문제에서 요구하는 답은 다음과 같다.

3. 두 번째 풀이 (미분방정식을 이용한 풀이) [목차]
미분방정식으로 푸는 아이디어는 간단하다. 초기 정적 평형을 이루고 있던 기체 구 표면의 입자가 기체 구의 중심으로 중력을 받으면서 선형 운동을 할 것이고 이때 가속도와 속도 및 거리에 관한 식이 오로지 시간 t에 대한 함수로 표현될 것이다. 따라서 적절한 변수분리법을 이용하여 a(t), v(t), R(t)를 구하는 과정을 보일 것이다.
초기 기체구의 반지름을 R0, 질량을 M, 기체구의 밀도를 ρ라 할 것이다. 그리고 R(t)를 시간 t에서 기체 구의 중심과 기체 구 표면의 입자 사이의 거리라고 볼 것이며, 이에 따라 -v(t) = -dR/dt는 가까워지는 속도, -a(t) = -dv/dt는 가까워지는 가속도라고 볼 수 있다. 우선 중력가속도에 대한 식 |a| = GM / R2이라는 식을 통해 ⑴ 식을 얻을 수 있다.
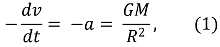
이때 dt를 넘기고 양변에 -v = -dR/dt를 곱하면 ⑵ 식을 얻을 수 있다.
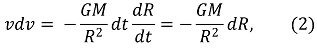
이때 양변을 0에서 t까지의 시간 구간동안 적분하면, 초기속도가 0이라는 조건에 따라 ⑶ 식을 얻을 수 있다.
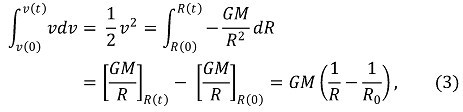
따라서 v와 R에 대한 ⑷ 식을 얻게 된다. 단, 이때 기체 구 표면의 입자가 R이 줄어드는 방향으로 속도 성분을 갖기 때문에 v < 0이다.
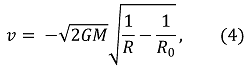
그런데 v는 v = dR/dt로 표현될 수 있기 때문에 ⑷ 식에 대입하면 미분방정식 ⑸ 식을 얻는다.
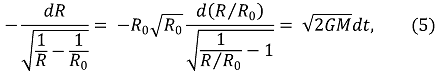
만약 별이 형성될 때 R이 0까지 응축하게 된다면 그 시간을 구하는 과정은 다음과 같다.

그런데 다음과 같은 치환을 생각해 볼 수 있다.
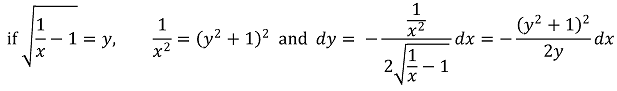
복잡한 적분식은 다음과 같이 귀결된다.
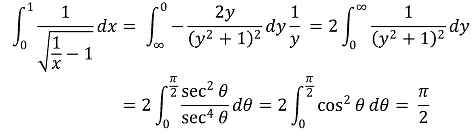
따라서 T는 위 첫 번째 풀이에서 구한 결과가 나온다.

그럼에도 이 번거로운 방법의 장점은 원시별이 진화하는 과정에서 존재하는 개념인 한계응축비율 min(R / R0) = L에 대한 시간도 표현할 수 있다는 것이다.
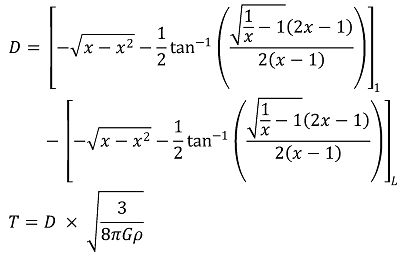
입력: 2022.09.03 00:55
'▶ 자연과학 > ▷ 지구과학' 카테고리의 다른 글
| 【지구과학】 2-1강. 쌍성계의 공전면이 한 평면임을 증명 (0) | 2022.09.03 |
|---|---|
| 【지구과학】 4-1강. 우주 산업 (0) | 2022.08.28 |
| 【지구과학】 지구과학 목차 (0) | 2020.01.12 |
| 【지구과학】 16강. 지구온난화 (0) | 2019.08.16 |
| 【지구과학】 15강. 지구의 역사 (0) | 2019.08.16 |




최근댓글