웹툰 킬더킹 : 결함게임
추천글 : 【논리학】 수학 논리 문제 (21~40)
결함 게임의 규칙

우선 게임의 규칙을 제대로 이해할 필요가 있다. 선공이 카드 2장 중 한 장에 후공의 킹 카드가 있다는 것을 확신했다고 가정하자. 위에 써 놓은 규칙에 따르면 선공이 후공의 킹 카드를 제대로 지목했든, 그러지 못했든 결과적으로 단 한 번의 질문으로 선공이 후공의 킹 카드의 위치를 알게 되므로 선공의 승리가 될 것만 같다. 하지만 웹툰에 나온 내용에 따르면 그런 것은 아니었다. 따라서 승리의 조건이 킹 카드의 위치를 아는지의 여부가 아니라 정확히 킹 카드의 위치를 '지목'했는지의 여부일 것이다. 그렇다면 질문의 종류는 킹 카드의 위치를 '추리는 것'과 킹 카드의 위치를 '지목하는 것'으로 두 종류가 있다는 것을 알 수 있다.
한 차례의 질문으로 킹 카드의 범위를 추리기 위해서는 킹 카드가 있는 조합과 없는 조합으로 반씩 쪼개는 것이 이상적이며, 이를 웹툰에서는 '반반 전략'이라고 소개하고 있다.
1,000,000보다 작은 임의의 숫자를 맞추기 위해 몇 번의 질문이 필요할까? 예/아니오로 대답이 제한된다면, 정답은 20번이었다. 2개의 숫자 중 하나를 고르는 데는 질문 하나면 된다. 숫자가 4개였다면 질문 두 번, 8개라면 질문 세 번이 필요하지만, 16개라면 네 번, 32개라면 다섯 번, 질문 기회가 늘어나면 가려낼 수 있는 숫자는 기하급수로 커진다. 20번의 질문 기회가 있다면 1,048,576의 숫자 중에서 하나를 고를 수 있다. 1,000,000은 1,048,576보다 작은 수이기 때문에 20번의 질문이면 충분하다. 반씩 나누어 가면 답은 금방 나온다. 기하급수의 무서움을 반대로 적용한 예랄까, 체스판의 첫 칸에 쌀알 하나를 놓고 다음 칸으로 옮길 때마다 그 두 배의 쌀알을 놓는다면? 그 쌀알을 대느라 왕국이 파산했다는 이야기, 계산하면 쌀의 수는 18,446,744,043,709,551,616 톨이다. 즉 반대로 말하면, 18,446,744,073,709,551,616 톨의 쌀알에서 한 알의 쌀이 남는 데 64번의 질문이면 충분하다는 뜻이다.
웹툰에서 남주는 결함 게임의 룰이, 선공이 24장, 후공이 32장, 총 56장으로 게임을 하면 두 쪽 모두 승률이 반이 된다고 언급했다. 그래서 이렇게 불편한 룰이 어딘지 모를 '결함'이 있는 것이라고 추론했다. 그렇다면 남주는 56장을 사용하면 승률이 반이 된다는 결론은 어디서 얻었을까?
f (a, b)를 a개의 카드를 가지고 있는 선공과 b개의 카드를 가지고 있는 후공이 승부를 해서 선공이 이기게 되는 확률이라고 정의하자. 단, 선공과 후공의 카드 선택지의 범위는 겹치지 않는다. a와 b가 작지 않은 수라고 할 때 킹 카드의 위치를 추리는 질문만 하는 것이 절대적으로 유리하다. 그때 f 에서 다음과 같은 점화식을 찾을 수 있다.

위 점화식에서 b가 홀수인 경우에 대해 첨언하자면, 한 차례의 질문으로 t 개 또는 t + 1 개의 원소로 이루어진, 킹 카드가 포함된 구간을 특정할 수 있고, 그 뒤 확률의 곱셈 및 덧셈 법칙을 적용한 것이다. 참고로 1 - f (a, b)는 후공이 이길 확률이다.
따라서 f (24, 32) = 1 - f (16, 24) = f (12, 16) = 1 - f (8, 12) = f (6, 8) = 1 - f (4, 6) = f (3, 4) = 1 - f (2, 3)이다. 그런데 a = 2, b = 3 인 경우는 작은 수이다. 즉, 무턱대고 킹 카드의 위치를 추리는 질문만 하는 것은 어리석은 선택이다. 왜냐하면 킹 카드의 위치를 지목하면서 킹 카드의 위치를 추리는 것이 가능하기 때문이다. 따라서 a 또는 b (혹은 둘 모두)가 특정 수 이하로 작아지면 킹 카드의 위치를 지목하는 질문만 하는 것이 절대적으로 유리하다.
가령, a = n (≥ 1)이고 b = 2라면 선공의 입장에서 지목을 하든, 위치를 추리는 질문을 하든 킹 카드의 위치를 알 수 있고, 지목을 하면 운 좋게 한 번에 킹 카드의 위치를 맞출 수 있으므로 지목을 하는 질문을 하는 것이 무조건 좋다. 만약 선공이 킹 카드의 위치를 못 맞췄으면 후공에게 공격권이 주어진다. 후공의 입장에서 주어진 첫 기회에 선공의 킹 카드의 위치를 맞추지 못하면 그 다음 턴에서 선공이 게임에서 이길 수밖에 없다. 따라서 후공은 반드시 선공의 카드이 위치를 지목해야 한다. 따라서 f (n, 2)는 다음과 같다.
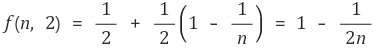
위와 같이 생각하면 f (2, 3)은 다음과 같다.

따라서 남주의 주장은 타당했다.
이제 본 문제로 돌아가자. 제시된 결함 게임은 선공과 후공의 카드 선택지의 범위가 겹침으로써 의도하지 않게 상대편에게 자신의 카드의 힌트를 주게 되는 상황이 발생하는 게 핵심이다. 이 때문에 '결함'이라는 이름이 붙은 것이다. 예를 들어 선공이 "카드의 범위가 17보다 크거나 같은가?"라고 물어보았다고 생각해 보자. 분명 선공은 자신의 카드를 제외한 32장의 카드에서 킹 카드의 범위를 줄이려는 시도를 할 것은 분명하다. 이는 후공도 알고 있는 사실이다. 따라서 선공이 1 ~ 16과 17 ~ 33까지로 구간을 나누었다는 사실로부터 후공은 뭔가를 알아챌 것이다. 왜냐하면 1 ~ 16까지는 16개의 숫자가 있고, 17 ~ 33까지는 17개의 숫자가 있으며, 선공의 입장에서 분명 반반으로 나누었다고 생각할 것이기 때문이다. 따라서 후공이 생각하기에, 선공의 킹 카드 숫자는 17 ~ 25까지여서 선공이 보기에 17 ~ 33까지의 수 중 후공의 킹 카드 숫자의 선택지가 16개라고 생각했다고 결론 지을 것이다.
따라서 애초에 상대방에게 자신의 킹 카드의 위치에 대한 힌트를 주지 않기 위해서 선공은 1 ~ 33의 숫자를 모두 고려하고, 후공은 1 ~ 25의 숫자를 모두 고려해야 할 것이다. 즉, 선공이 이길 확률은 f (25, 33)이다. 이를 간단한 코딩을 통해 확인해 본 결과 선공이 이길 확률은 0.523636이었다.
#include
<stdio.h>
double f(int a, int b);{
if (b == 1) return 1.0;
if (b == 2) return 1 - 0.5 / a;
if (a == 1) return 1 / b;
if (a == 2 && b == 3) return 0.5;
if (b % 2 == 0) return 1 - f(b/2, a);
double t = (b - 1) / 2;
return (t/b) * (1-f(t, a)) + ((t+1)/b) * (1-f(t+1,a));
}
int main() {
printf("%lf", f(25, 33));
return 0;
}
아직 고려할 사항이 더 남았다. 만약 선공의 킹 카드와 후공의 킹 카드가 인접하거나 매우 가까이 있는 경우 상대편의 킹 카드의 범위를 추리는 과정에서 자신의 킹 카드의 위치 정보로 상대편의 킹 카드의 위치를 추론하는 상황도 분명 있을 것이다. 가령 상대편의 카드 선택지가 둘 중 하나인데, 그 중 하나가 자신의 카드라면, 바로 상대편의 킹 카드의 위치를 알 수 있을 것이다. 킹 카드가 인접할 확률이 5 %인데, 이는 무시할 숫자는 아닌 것 같다. 따라서 결과적으로 선공이 우세한지, 후공이 우세한지 확신하기는 어려울 것 같다. 중요한 점은 어느 쪽이든 승률이 50 % 근처일 것이므로 비교적 '공평한' 게임이 될 것 같다는 점이다.
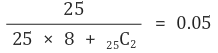
앞서 결함 게임의 결함이 상대편의 카드 범위를 물어보는 과정에서 자신의 킹 카드의 위치 정보를 넘겨주게 되어 오히려 선공이 불리하다고 했다. 하지만 이를 역이용 해서 Fake Attack을 시도하는 것도 좋을 것 같다. 실은 자신의 킹 카드가 17 미만인데 "카드의 범위가 17보다 크거나 같은가?"라고 물어본다면, 후공은 엉뚱한 데를 노리고 있을 것이다. 그렇다면 한 차례 이상 후공의 질문을 무력화할 수 있다. 만약 선공의 운이 별로 좋지 않아, 후공의 킹 카드의 위치가 17 이상이었고, 후공이 선공의 표정을 읽어 자신이 속았다는 것을 바로 깨달았다고 하자. 그 뒤 서로 자신의 킹 카드 위치 정보를 흘리지 않기 위해 서로의 카드가 독립인 것마냥 플레이한다고 하자. 그렇다면 선공의 승률은 얼마일까? 그 값은 f (16, 17)과 같고, 위 코딩을 통해 구해본 결과 0.705882 정도였다. 그런데 이 값은 선공이 운이 별로 좋지 않다고 가정했을 때의 값이다. 따라서 후공 입장에서 상대편이 흘린 정보를 마냥 덥썩 물 수도 없게 된 셈이다. 개인적으로 이 웹툰의 작가가 제시한 결함이란 게 과연 결함이 맞는지 의심스럽고, 이 결함게임은 두 개의 증거를 감안해 볼 때 오히려 선공한테 유리한 게임일 것 같다.
2016.06.28 21:37
'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글
| 【논리학】 수학 논리 문제 [21~40] (7) | 2023.10.12 |
|---|---|
| 【논리학】 수학 논리 문제 [01~20] (13) | 2023.09.09 |
| 【논리학】 더지니어스 전략윷놀이 복기 (최연승 vs 임요한) (0) | 2018.02.15 |
| 【논리학】 더지니어스 전략윷놀이 복기 (성규 vs 차민수) (0) | 2018.02.15 |
| 【수학】 수학 목차 (0) | 2016.06.26 |





최근댓글