본문 바로가기
▶ 자연과학/▷ 암호·보안
Contact English

【국가암호공모전】 (II-A 분야) 문제 06 - 2부 (2016)

초록E 2016. 8. 15. 09:11

 

국가암호공모전 (II-A 분야) 문제 06 - 2부 (2016)

 

추천글 : 【암호론】 암호론 목차

2. 풀이 [본문]

a. RSA 알고리즘

 

2. 풀이 [목차]

우선 Fermat factorization에 대해서 간단히 정리하도록 하자.

 

a = [sqrt(n)] + 1;
while(1){
    b2 = a*a - n;
    if(SquareNumberCheck(b2) == 1)
        break;
    a ++;
}
printf("%d %d", &a, &b);

 

이때 n은 분명 두 소수의 곱이어서 n = a2-b2, a = (p+q)/2, b = (p-q)/2으로 표현된다는 사실을 상기할 수 있다. 이 방법은 p와 q의 차이가 작을수록 빛이 난다. 혹은 p와 q의 비율을 안다면 a의 초기값을 조절함으로써 똑같이 효율적으로 풀 수 있을 것이다. 문제에서 추천한 방법이므로 이 방법이 먹히길 바랄 뿐이다.

 

우선 [sqrt(n)]을 구하기 위해 다음 코드를 실행시켰다. 함수들은 bignum.c에서 따왔다. (그러나 bignum.c가 10진법에 최적화돼 있으므로 이를 16진법에 대한 것으로 바꾸었다. 이를 위해 "%10", "/10" 따위와 print_bignum에서 출력 범위만 고치면 충분하다.) 그리고 그 결과는 다음과 같다.

 

int i;
bignum a;
char* n = // n is pow(16, 511) ~ pow(16, 512)
"84DF9A0A2EF48193B9C0ED3857F2C04B"\
"74636F8270E721D58FB85903EB7460EB"\
"94091120562C6F7F7A81859B9822B217"\
"E0FBBA703F80574E87B5ECCA4B409569"\
"4BF9D99D3F8E94983770AD04482297E9"\
"61C9E75CA9ACF0854E914C07AAA8005D"\
"79CF1B7B7951AD3B87DF660E731D0918"\
"5960206C3D2C52E0F1F7765561FF76B6"\
"447D6509F97C407336D9E3ED00FDEF01"\
"C7D81F291BB2F498897D1BEA552A3086"\
"915FA887D0FAAD2F768C17DB03B68F74"\
"1B8EE36AFFF1809CC96E22F46FF2192A"\
"2F3D1D5E7E929FEF0414B520AA9D3551"\
"14F76AFA0FDB0CF2C6A9DBED57ADD80E"\
"C0598C892857C9772D91552B625BEB5C"\
"13BDE94E95528AA74A9045D589327179";

int_to_bignum(1, &a);
make_a_into_16_to the_255_pow(&a); // a = 16^255

for(int i = 255; i >= 0; i --){
    here:
    
    multiply_bignum(&a, &a, &note1);
    if(compare_bignum(&n, &note1) == MINUS){    // n > note1
        a.digits[a.lastdigit - (255 - i)] ++;   // quite important
        goto here;
    }
    else
        a.digits[a.lastdigit - (255 - i)] --;   // to make a smaller than n
}
print_bignum(&a);   // print a

 

B8 6E E5 90 C3 43 0E 70 11 8F 37 05 6C 2E 2A 95
31 FF BB 69 1B D6 B9 12 6A 04 69 44 F7 04 DB 13
2D A0 97 00 5E A0 26 DC 64 89 84 25 41 E3 C2 2E
DE 5B 31 B4 02 64 D0 F7 09 EB A3 F5 94 61 5F 58
5B 6E 35 EA CC 0F 8D EF 0F E9 22 F5 FD 98 42 B2
10 C9 E8 CB CB AA 41 8A 4E EA 27 7F 33 14 B3 CB
82 F1 56 2D 7B 82 AA E7 65 EB 9E 8F 27 42 4F F8
28 C8 FF A2 14 5C 40 06 FD 3C D1 35 91 91 5F 3C

 

이제 맨 마지막의 -3C를 -3D로 바꾼 값을 a의 초기값으로 두고 Fermat factorization을 적용하자. 코드를 수정하는 과정에서 n의 명칭이 n1, a의 명칭이 n2, b2의 명칭이 note3로 바뀌었음을 이해해 주길 바란다. 다음 코드를 돌려본 결과 놀랍게도 0.438초만에 정답이 도출됐다.

 

main(){
    int i, j, k = 0;
    bignum n1, n2;
    bignum nt1, nt2, nt3, nt4, nt5;
    bignum note1, note2, note3, note4, note5;

    initialize_bignum(&n1);
    initialize_bignum(&n2);
    int_to_bignum(1, &nt1);
    int_to_bignum(10, &nt2);
    int_to_bignum(0, &nt3);
    int_to_bignum(2, &nt4);
    int_to_bignum(16, &nt5);

    char* key =
    "84DF9A0A2EF48193B9C0ED3857F2C04B"\
    "74636F8270E721D58FB85903EB7460EB"\
    "94091120562C6F7F7A81859B9822B217"\
    "E0FBBA703F80574E87B5ECCA4B409569"\
    "4BF9D99D3F8E94983770AD04482297E9"\
    "61C9E75CA9ACF0854E914C07AAA8005D"\
    "79CF1B7B7951AD3B87DF660E731D0918"\
    "5960206C3D2C52E0F1F7765561FF76B6"\
    "447D6509F97C407336D9E3ED00FDEF01"\
    "C7D81F291BB2F498897D1BEA552A3086"\
    "915FA887D0FAAD2F768C17DB03B68F74"\
    "1B8EE36AFFF1809CC96E22F46FF2192A"\
    "2F3D1D5E7E929FEF0414B520AA9D3551"\
    "14F76AFA0FDB0CF2C6A9DBED57ADD80E"\
    "C0598C892857C9772D91552B625BEB5C"\
    "13BDE94E95528AA74A9045D589327179";

    char* initial_value =
    "B86EE590C3430E70"\
    "118F37056C2E2A95"\
    "31FFBB691BD6B912"\
    "6A046944F704DB13"\
    "2DA097005EA026DC"\
    "6489842541E3C22E"\
    "DE5B31B40264D0F7"\
    "09EBA3F594615F58"\
    "5B6E35EACC0F8DEF"\
    "0FE922F5FD9842B2"\
    "10C9E8CBCBAA418A"\
    "4EEA277F3314B3CB"\
    "82F1562D7B82AAE7"\
    "65EB9E8F27424FF8"\
    "28C8FFA2145C4006"\
    "FD3CD13591915F3D";

    for(i = 0; i < 512; i ++){
        if(key[511-i] >= '0' && key[511 - i] <= '9')
            n1.digits[i] = key[511 - i] - '0';
        else    n1.digits[i] = key[511 - i] - 'A' + 10;
    }
    n1.lastdigit = 511;


    for(i = 0; i < 256; i ++){
        if(initial_value[255 - i] >= '0' && initial_value[255 - i] <= '9')
            n2.digits[i] = initial_value[255 - i] - '0';
        else    n2.digits[i] = initial_value[255 - i] - 'A' + 10;
    }
    n2.lastdigit = 255;

    while(1){
        multiply_bignum(&n2, &n2, &note1);
        subtract_bignum(&note1, &n1, &note2);   // note2 = n2^2 - n1

        /* for optimization */
        if(note2.digits[0] != 0 &&
           note2.digits[0] != 1 &&
           note2.digits[0] != 4 &&
           note2.digits[0] != 9)    continue;

        /* check whether note2 is square number or not */
        int_to_bignum(1, &note3);
        for(i = 0; i <= (note2.lastdigit + 1) / 2; i ++){
            multiply_bignum(&note3, &nt5, &note1);
            add_bignum(&note1, &nt3, &note3);
        }

        for(i = note3.lastdigit; i >= 0; i --){
            here:

            multiply_bignum(&note3, &note3, &note4);
            if(compare_bignum(&note2, &note4) == MINUS){
                note3.digits[i] ++;
                goto here;
            }
            else
                note3.digits[i] --;
        }

        if(compare_bignum(&note2, &note4) == 0)
            break;

        add_bignum(&n2, &nt1, &note1);
        add_bignum(&note1, &nt3, &n2);

        k ++;
        if(k % 10 == 0)
            printf("%d\n", k);
    }

    print_bignum(&n2);
    printf("\n");
    note3.digits[0] ++;
    print_bignum(&note3);

}

 

 

a의 초기값으로 설정한 게 바로 정답이었던 것이다. 그리고 두 번째 값에서 맨 앞에 0이 있는 이유는 코드 상의 사소한 실수인 것으로 추정된다. 한편 위의 값이 (p+q)/2이고, 아래의 값이 (p-q)/2이므로 p, q를 구하는 과정은 굉장히 단순하다. 과정은 생략하고 그 값을 기술하면 다음과 같다.

 

// max(p,q)
B8 6E E5 90 C3 43 0E 70 11 8F 37 05 6C 2E 2A 95
31 FF BB 69 1B D6 B9 12 6A 04 69 44 F7 04 DB 13
2D A0 97 00 5E A0 26 DC 64 89 84 25 41 E3 C2 2E
DE 5B 31 B4 02 64 D0 F7 09 EB A3 F5 94 61 5F 58
5B 6E 35 EA CC 0F 8D EF 0F E9 22 F5 FD 98 42 B2
10 C9 E8 CB CB AA 41 8A 4E EA 27 7F 33 14 B3 CB
F6 3A C8 94 91 CD 81 29 21 7C 85 0F E9 EF 19 C5
9D 38 ED E6 05 41 50 19 3C 60 F1 54 AF DB C3 59

// min(p,q)
B8 6E E5 90 C3 43 0E 70 11 8F 37 05 6C 2E 2A 95
31 FF BB 69 1B D6 B9 12 6A 04 69 44 F7 04 DB 13
2D A0 97 00 5E A0 26 DC 64 89 84 25 41 E3 C2 2E
DE 5B 31 B4 02 64 D0 F7 09 EB A3 F5 94 61 5F 58
5B 6E 35 EA CC 0F 8D EF 0F E9 22 F5 FD 98 42 B2
10 C9 E8 CB CB AA 41 8A 4E EA 27 7F 33 14 B3 CB
0F A7 E3 C6 65 37 D4 A5 AA 5A B8 0E 64 95 86 2A
B4 59 11 5E 23 77 2F F4 BE 18 B1 16 73 46 FB 21

// φ(n)
84 DF 9A 0A 2E F4 81 93 B9 C0 ED 38 57 F2 C0 4B
74 63 6F 82 70 E7 21 D5 8F B8 59 03 EB 74 60 EB
94 09 11 20 56 2C 6F 7F 7A 81 85 9B 98 22 B2 17
E0 FB BA 70 3F 80 57 4E 87 B5 EC CA 4B 40 95 69
4B F9 D9 9D 3F 8E 94 98 37 70 AD 04 48 22 97 E9
61 C9 E7 5C A9 AC F0 85 4E 91 4C 07 AA A8 00 5D
79 CF 1B 7B 79 51 AD 3B 87 DF 66 0E 73 1D 09 18
59 60 20 6C 3D 2C 52 E0 F1 F7 76 55 61 FF 76 B4
D3 9F 99 E8 72 F6 23 93 13 BB 75 E2 28 A1 99 D7
63 D8 A8 56 E4 05 82 73 B5 74 49 60 67 20 7A 60
36 1E 7A 87 13 BA 5F 76 AD 79 0F 90 7F EF 0B 16
5E D8 80 02 FB 27 DE AE B5 96 DB 09 47 2F 5A 79
78 60 B1 88 E6 73 84 10 E4 42 6F 34 AF 6C AF EC
F3 63 99 62 78 86 89 DE 28 D5 8C EE F1 84 70 77
BA 76 E0 2E 31 52 73 A8 61 BA 18 0D 13 D7 4B 6B
C2 2B EA 0A 6C 9A 0A 99 50 16 A3 6A 66 0F B3 00

 

이제 private exponent를 구하자. public modulus(n)와 public exponent(e)가 주어져 있다고 할 때, private exponent(d)는 다음과 같이 정의된다; e × d ≡ 1 (mod φ(n)). d를 구하기 위해 다음 mod 연산의 성질을 활용하고자 한다.

 

 

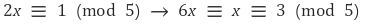
이때 곱해지는 수(3)는 괄호 안의 수(5)와 서로 소여야 한다. 이 방법을 십분 활용해서 d의 값을 구해보자.

 

int divisor_check(bignum *a, bignum *b){
    bignum note1, note2;
    divide_bignum(a, b, &note1);
    multiply_bignum(&note1, b, &note2);
    if(compare_bignum(&note2, a) == 0)
        return 1;
    return 0;
}

main(){
    int i;
    bignum n1, n2, n3;  // note that n3 will become d, the inverse of e
    bignum nt1, nt2, nt3;
    bignum note1, note2, note3, note4, note5, note6;

    initialize_bignum(&n1);
    initialize_bignum(&n2);
    int_to_bignum(0, &nt1);
    int_to_bignum(1, &nt2);
    int_to_bignum(2, &nt3);

    char* phi_n =
    "84DF9A0A2EF48193B9C0ED3857F2C04B"\
    "74636F8270E721D58FB85903EB7460EB"\
    "94091120562C6F7F7A81859B9822B217"\
    "E0FBBA703F80574E87B5ECCA4B409569"\
    "4BF9D99D3F8E94983770AD04482297E9"\
    "61C9E75CA9ACF0854E914C07AAA8005D"\
    "79CF1B7B7951AD3B87DF660E731D0918"\
    "5960206C3D2C52E0F1F7765561FF76B4"\
    "D39F99E872F6239313BB75E228A199D7"\
    "63D8A856E4058273B574496067207A60"\
    "361E7A8713BA5F76AD790F907FEF0B16"\
    "5ED88002FB27DEAEB596DB09472F5A79"\
    "7860B188E6738410E4426F34AF6CAFEC"\
    "F3639962788689DE28D58CEEF1847077"\
    "BA76E02E315273A861BA180D13D74B6B"\
    "C22BEA0A6C9A0A995016A36A660FB300";

    char* e = "10001";

    for(i = 0; i < 512; i ++){
        if(phi_n[511-i] >= '0' && phi_n[511 - i] <= '9')
            n1.digits[i] = phi_n[511 - i] - '0';
        else    n1.digits[i] = phi_n[511 - i] - 'A' + 10;
    }
    n1.lastdigit = 511;
    for(i = 0; i < 5; i ++){
        if(e[4 - i] >= '0' && e[4 - i] <= '9')
            n2.digits[i] = e[4 - i] - '0';
        else
            n2.digits[i] = e[4 - i] - 'A' + 10;
    }
    n2.lastdigit = 4;
    int_to_bignum(1, &n3);

    while(1){
        if(n2.lastdigit == 0 && n2.digits[0] == 1)
            break;

        if(n2.lastdigit == 3 && n2.digits[0] == 13)  // 9A2D
            int_to_bignum(7, &note5);
        else if(n2.lastdigit == 3 && n2.digits[0] == 15) // 113F
            int_to_bignum(10, &note5);
        else if(n2.lastdigit == 2 && n2.digits[0] == 15) // AFF
            int_to_bignum(4, &note5);
        else if(n2.lastdigit == 2 && n2.digits[0] == 13) // A6D
            int_to_bignum(4, &note5);
        else if(n2.lastdigit == 2 && n2.digits[0] == 9) // 9A9
            int_to_bignum(2, &note5);
        else if(n2.lastdigit == 1 && n2.digits[0] == 11) // 2B
            int_to_bignum(7, &note5);
        else if(n2.lastdigit == 1 && n2.digits[0] == 1) // 11
            int_to_bignum(2, &note5);
        else if(n2.lastdigit == 0 && n2.digits[0] == 11) // B
            int_to_bignum(8, &note5);
        else if(n2.lastdigit == 0 && n2.digits[0] == 5) // 5
            break;
        else    int_to_bignum(4, &note5);

        here:
        multiply_bignum(&note5, &n1, &note6);
        divide_bignum(&note6, &n2, &note1);
        add_bignum(&note1, &nt2, &note2);
        multiply_bignum(&note2, &n2, &note3);
        subtract_bignum(&note3, &note6, &note1);
        if(divisor_check(&n1, &note1) == 1){
            add_bignum(&nt3, &note5, &note6);
            add_bignum(&note6, &nt1, &note5);
            goto here;
        }
        add_bignum(&note1, &nt1, &n2);
        multiply_bignum(&note2, &n3, &note4);
        if(compare_bignum(&note4, &n1) == MINUS){
            divide_bignum(&note4, &n1, &note1);
            multiply_bignum(&note1, &n1, &note2);
            subtract_bignum(&note4, &note2, &n3);
        }
        else    add_bignum(&note4, &nt1, &n3);

        // for check
        print_bignum(&n2);
        printf("\n");
        print_bignum(&n3);
        printf("\n\n");
    }
    // when n2 becomes 5, it makes troubles. so i did separate it from above.
    divide_bignum(&n1, &n2, &note1);
    add_bignum(&note1, &nt2, &note2);
    multiply_bignum(&note2, &n2, &note3);
    subtract_bignum(&note3, &n1, &note4);
    print_bignum(&note4);
    printf("\n");
    multiply_bignum(&note2, &n3, &note4);
    if(compare_bignum(&note4, &n1) == MINUS){
        divide_bignum(&note4, &n1, &note1);
        multiply_bignum(&note1, &n1, &note2);
        subtract_bignum(&note4, &note2, &n3);
    }
    else    add_bignum(&note4, &nt1, &n3);
    print_bignum(&n3);

    printf("\n\n>> review\n");
    initialize_bignum(&n2);
    for(i = 0; i < 5; i ++)
        n2.digits[i] = e[4 - i] - '0';
    n2.lastdigit = 4;
    multiply_bignum(&n2, &n3, &note1);
    divide_bignum(&note1, &n1, &note2);
    multiply_bignum(&note2, &n1, &note3);
    subtract_bignum(&note1, &note3, &note4);
    print_bignum(&note4);
    system("pause");
}

 

 

이때 d의 값은 "BF2A34..."이다. 위 소스를 보면 while문 내에 if문이 여러 개 있는 것을 알 수 있다. 이는 바로 앞에서 언급한 서로 소 조건을 만족시키기 위해서다. 생각보다 φ(n)이 약수가 많아서(ex. 2, 3, 7, 13) if문의 개수가 많았던 것이다. 그리고 e의 값이 5가 되었을 때 처리하기 꽤 까다로워서 따로 빼서 계산했다. (참고로 if문이 없으면 e가 특정 몇 개의 값들을 번갈아 취하면서 무한 반복을 하게 된다.) 한편, 가장 마지막에 review라고 해 놓은 것은 e × d가 법 φ(n)에 대해 나머지가 1인지 검토해 본 것인다. 보이는 대로 성공적이다!

 

이제 flag.hwp.enc 파일을 flag.txt 파일로 바꾸어 보자.

 

cd C:\Users 

ren flag.hwp.enc flag.txt 

 

그러면 참으로 해괴한 문자들을 발견할 수 있다.

 

 

이러한 현상이 일어나는 이유는 사실 숫자에 대한 정보를 저장하고 있는 flag.txt를 억지로 문자화시켰기 때문이다. 이제 이렇게 변환시킨 text 파일을 C에서 읽어들인 뒤 하나하나 숫자로 변환시켜 보면 다음 16진수 숫자열을 얻을 수 있다. (참고로 코드에서 366이라는 숫자는 시행착오를 통해 얻어진 숫자이다.)

 

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int i;
    long long int ch;
    char buffer[1000] = {0};
    char note[3] = {0};
    FILE *in = fopen("flag.txt", "r+");
    FILE *out = fopen("real_flag.txt", "w+");
    for(i = 0; i < 366; i ++){
        ch = getc(in);
        sprintf(note, "%0X", ch);
        if(note[1] == 0){
            note[1] = note[0];
            note[0] = '0';
        }
        buffer[2 * i + 1] = note[1];
        buffer[2 * i] = note[0];
        note[1] = 0;
        note[0] = 0;
    }
    fputs(buffer, out);
    fclose(in);
    fclose(out);
    return 0;
}

 

2E DC 22 1D CC 00 B3 2F 75 24 D1 ED 90 2F D6 63
A9 03 B8 93 68 16 B3 6C 5C 6C 62 13 64 11 9A 1C 
42 3E 72 03 89 8E 01 C2 70 D5 4D DA 91 F6 0E C1 
F5 0C 31 8A C9 CE A0 5F 71 6A 3F 54 D2 34 60 07 
13 D6 CF 41 61 02 2D E1 56 39 AB F6 6B 61 10 D3 
F2 A8 85 74 B7 4B 0C 68 D7 1D FD 7B 96 32 51 C4 
02 C2 11 FE 77 67 58 FB 26 12 47 B5 75 97 80 28 
40 A7 69 EC 13 EE 1C 17 20 3F 64 24 A9 1C 35 9E 
4C EA 61 22 F8 AB 9D C3 31 51 97 4E 54 0E 6C 06 
8C 63 64 94 C1 A8 AB A8 81 B8 FD 5F 77 48 BD 54
B2 EA FE 05 4B 42 FF 72 2C 7A C6 69 2A E3 C0 CE 
5A 07 5C D3 60 F1 8F 5B 09 D5 40 F0 93 44 8B EA 
80 AD 06 2E 2F C9 68 14 F0 29 22 C1 77 80 AC 01 
10 B9 15 9F DB 0A 56 0C 56 50 F3 05 13 38 50 64 
59 0C E3 8A CA 98 35 44 B4 82 6F 67 63 E9 80 E9 
11 01 BE 42 23 92 3B D4 1F B5 EB D0 C1 13 C5 F8 
C8 D8 F2 3C 7F 46 5F AF 36 86 0C 87 8F D5 F1 94
36 65 83 39 71 A3 46 35 D5 81 DF BE 8A D5 F0 79
7A 4C 27 6F 7C F7 F8 11 DD 89 6A 9A 0A 5E 8A 93
32 9B CE AC BE 2D 7E A9 93 BE 41 F7 A9 7A 0E 4B
6D D7 5E D5 43 4F F1 57 A5 7B 0A 94 51 D2 FF DA
E8 92 0B 99 94 A9 14 D8 B7 24 8E B7 64 0F 28 EF
7E AD 29 FB 5E 44 DD F2 E7 81 CE B8 B3 56

 

솔직히 말하면 이 과정부터 더 나아가지 못하고 있다. 왜냐하면 위의 정보는 16의 배수가 아니기 때문이다. 딱 4 bytes가 부족한데, 이것은 aeskey가 암호화됐을 때 맨 앞의 네 수가 모두 0이어야 하는데, 그 확률이 얼마나 될까. 실제로 그렇게 맞춰서 복호화를 시도해 주었음에도 16 bytes로 복호화되지 않았다. 중간에 실수는 없는지, 다른 경우는 없는지 더 고민해야 할 것 같다. 참고로 복호화 코드는 다음과 같다.

 

main(){
    int i, j = 0, temp, temp1, temp2, temp3, temp4;
    bignum modulus, private_key, public_key, message;
    bignum note1, note2, note3, note4, note5;
    // note1 would be decrypted message
    // note2 is "0"
    // note3, note4, note5 is just note

    initialize_bignum(&modulus);
    initialize_bignum(&private_key);
    initialize_bignum(&public_key);
    initialize_bignum(&message);
    int_to_bignum(0, &note2);

    char* Modulus=
    "00B2ECFB81FF280AA9BC4982E368A526C40857DF7AB591551A7F3787A92C2DBB"\
    "20131339A5A5FF3C4DA46964A4163B68B97105613B82A21AC4D852F39AC44BAA"\
    "5228CE58BBE5DA045C807D55CE7F4F06387E9D6B96B36704537FFE166DA19B97"\
    "C1AE70059CD970C42BBC8F31006A449A326C95541F27E170B12CA4468176DAF6"\
    "F8B24612BAF480A9A46DB6B70E26884058C3A193FEECEC335577FA82EB41A4B0"\
    "F4E1005C049C6D70CA0FBE9AC8981834B7A62342B48C7F4EE39045B838E7D0B7"\
    "E99683952CFCF7FC3939BA67604E2FD974FB2E8837385F14B94EE1030C73D19E"\
    "DBD5F5A3639BBE6D6979C77B59FCFE3373085274A499489F5BBFEEADD76E8C0E"\
    "AF";

    char *Private_key=
    "0273A0D69D2A6D4AFA1B7FC1A1F3715E8A46B9F73279B552D19F6F2A70428827"\
    "DE5B0B152BFB1D566B044EAEB8E7437E17005DDEB4E187C05EBE743C10A880C2"\
    "F370306312B9340A18709F365F24340F9E1C8616E08A6ED2BE143B36715A726F"\
    "E2F601FDAE350F5B12105C39873B3D69A7773C59D8F00BDD41A1569DFB84F091"\
    "5DF272621FCD6D5C65DFFFCF7BA3C6D8FFD0602834000C9CBC5B3031AB244656"\
    "495E3AE1527F11216D068032305861BA7F49D0636268A532EDF374D2D3B2340F"\
    "F0676EED2C9FB25E157E3C74D6C454E5656BD74D3BA0F07EFAFC17777CC2E909"\
    "02E492F5337327835D72241DA513CF293E673B53FBA39AAADB7FFA147DBC7601";

    char *Public_key=
    "010001";

    char *Message=
    "123456789";


    for(i = 0; i < 514; i ++){
        if(Modulus[513 - i] >= '0' && Modulus[513 - i] <= '9')
            modulus.digits[i] = Modulus[513 - i] - '0';
        else    modulus.digits[i] = Modulus[513 - i] - 'A' + 10;
    }
    modulus.lastdigit = 513;
    zero_justify(&modulus);

    for(i = 0; i < 512; i ++){
        if(Private_key[511 - i] >= '0' && Private_key[511 - i] <= '9')
            private_key.digits[i] = Private_key[511 - i] - '0';
        else    private_key.digits[i] = Private_key[511 - i] - 'A' + 10;
    }
    private_key.lastdigit = 511;
    zero_justify(&private_key);

    for(i = 0; i < 6; i ++){
        if(Public_key[5 - i] >= '0' && Public_key[5 - i] <= '9')
            public_key.digits[i] = Public_key[5 - i] - '0';
        else    public_key.digits[i] = Public_key[5 - i] - 'A' + 10;
    }
    public_key.lastdigit = 5;
    zero_justify(&public_key);

    for(i = 0; i < 9; i ++){
        if(Message[8 - i] >= '0' && Message[8 - i] <= '9')
            message.digits[i] = Message[8 - i] - '0';
        else    message.digits[i] = Message[8 - i] - 'A' + 10;
    }
    message.lastdigit = 8;
    zero_justify(&message);

/*
print_bignum(&message);

    int_to_bignum(1, &note1);
    for(i = 0; i <= public_key.lastdigit; i ++){
       // printf("%d\n", ++j);

        temp = public_key.digits[i];
        temp1 = temp % 2;   temp /= 2;
        temp2 = temp % 2;   temp /= 2;
        temp3 = temp % 2;   temp /= 2;
        temp4 = temp % 2;

        if(temp1){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);

        if(temp2){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);


        if(temp3){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);


        if(temp4){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);
    }
    add_bignum(&note1, &note2, &message);

print_bignum(&message);
*/

    int_to_bignum(1, &note1);
    j = 0;
    for(i = 0; i <= private_key.lastdigit; i ++){
      //  printf("%d\n", ++j);

        temp = private_key.digits[i];
        temp1 = temp % 2;   temp /= 2;
        temp2 = temp % 2;   temp /= 2;
        temp3 = temp % 2;   temp /= 2;
        temp4 = temp % 2;

        if(temp1){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);

        if(temp2){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);


        if(temp3){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);


        if(temp4){  // note1 = note1 * message mod modulus
            multiply_bignum(&note1, &message, &note3);
            divide_bignum(&note3, &modulus, &note4);
            multiply_bignum(&note4, &modulus, &note5);
            subtract_bignum(&note3, &note5, &note1);
        }

        multiply_bignum(&message, &message, &note3);
        divide_bignum(&note3, &modulus, &note4);
        multiply_bignum(&note4, &modulus, &note5);
        subtract_bignum(&note3, &note5, &message);
    }
    print_bignum(&note1);
    system("pause");
}

 

 입력: 2016.08.15 20:35

'▶ 자연과학 > ▷ 암호·보안' 카테고리의 다른 글

【보안】 보안 일반  (0) 2017.10.13
【국가암호공모전】 (II-A 분야) 문제 07 (2016)  (2) 2016.08.15
【국가암호공모전】 (II-A 분야) 문제 06 - 1부 (2016)  (3) 2016.08.15
【국가암호공모전】 (II-A 분야) 문제 05 (2016)  (5) 2016.08.14
【국가암호공모전】 (II-A 분야) 문제 04 (2016)  (10) 2016.08.14

'▶ 자연과학/▷ 암호·보안' 관련 포스팅

티스토리툴바