국가암호공모전 (II-A 분야) 문제 07 (2016)
추천글 : 【암호론】 암호론 목차
1. 문제 [본문]
2. 풀이 [본문]
1. 문제 [목차]
제공되는 윈도우용 프로그램 verifier.exe에서 검증에 성공하는 ECDSA 전자서명을 생성하고, 그 방법에 대해 암호학적으로 설명하시오. (전자서명은 signer.exe를 이용하여 생성할 수도 있다. 해쉬함수는 SHA-1임)
소수 p > 3에 대하여, 유한체 Fp ≅ Z/pZ 위에서 정의되는 타원곡선은 4a3+27b2 ≢ 0 (mod p)을 만족하는 만족하는 계수들 a, b ∊ Fp를 가지는 방정식 f (x, y) = y2 - x3 - ax - b = 0의 해집합에 무한원점 ∞을 추가한 점집합 E = {(x, y) | f (x, y) = 0} ∪ {∞}으로 정의될 수 있다. 이러한 타원곡선이 특정 연산에 대하여 군을 이룬다는 것은 잘 알려진 사실이며(See here), E의 위수가 큰 부분군 상의 이산로그문제(Discrete Logarithm Problem)를 기반으로 만들어지는 암호를 타원곡선암호(ECC : Elliptic Curve Cryptography)라 한다.
(주석: 조건 4a3+27b2 ≢ 0 (mod p)은 특이점(즉 (0,0))이 생기지 않을 조건이다. 이 조건은 실제로 실수체 타원곡선에서 특이점이 생기지 않을 조건(x3 + ax + b = 0이 x 축과 접하지 않을 조건)에서 비롯된다. 이렇게 실수체 타원곡선에서 발견되는 다양한 조건이 유한체 타원곡선에도 적용되는데, 이를 증명하기 위해서는 복잡한 군이론이 사용된다. 하지만 여기에서 비교적 간단(?)한 증명을 발견할 수 있었다.)
(주석: 타원곡선에서 무한원점 ∞이 있으면 + 연산은 기하적으로 정의되고, 그것은 Abelian group을 형성한다는 것이 잘 알려져 있다. (See here) 따라서 덧셈과 곱셈에서 성립하는 법칙처럼 교환법칙, 결합법칙, 분배법칙이 성립한다. 또한 위에서 특이점이 생기는 것을 피한 까닭도 덧셈이 모든 점에서 잘 정의될 수 있도록 하기 위함이다. 그리고 아래 그림에서 P + Q = -R이다.)

(주석: P, Q가 주어질 때 Q = nP인 n을 계산할 수 있을까? 이러한 문제를 로그 문제(Logarithm problem)라고 한다. 이때 로그라고 부르는 까닭은 # 풀이에서 보게 될 double and add 알고리즘이 로그 시간만큼 요구하기 때문이다. 이때 타원곡선의 실수공간을 이산공간으로 축소했을 때, 다음 Q ≡ nP (mod p)인 n을 구하는 것을 이산로그문제(Discrete logarithm problem)라고 한다.)
유한체 Fp 상에서 타원곡선암호를 사용할 때에는 다음과 같은 값들을 도메인 파라미터로 공유한다.
⑴ Fp를 정의하는 소수 p.
⑵ 곡선의 계수들 a, b.
⑶ E(Fp)의 한 생성점 G. (생성점이란, 타원곡선 E(Fp)상에 놓이는 점들을 지칭한다.)
⑷ G의 위수 n. (위수(order)란, n·G ≡ 0 (mod p)인 최소의 n를 지칭한다.)
타원곡선 전자서명 알고리즘 ECDSA는 다음과 같은 방식으로 수행된다.
[키 생성]
0 < d < n인 난수 d를 생성하여, d를 개인키로 점 Q = dG를 공개키로 취한다.
[서명 생성]
⑴ 서명할 메시지 m의 해쉬값 h = hash(m)을 계산한다.
⑵ 난수 k를 뽑아 점 kG의 x좌표 x(kG)에 대해, r = x(kG) (mod n)를 계산한다.
⑶ s = k -1 (h + dr) (mod n)를 계산한다.
⑷ m에 전자서명 = (r, s)
[서명 검증]
⑴ 검증할 메시지 m의 해쉬값 h = hash(m)를 구한다. (서명 시와 같은 해쉬함수 사용)
⑵ u1 = hs -1 (mod n), u2 = rs -1 (mod n)를 계산하고,
⑶ (u1G + u2Q의 x좌표) ≡ r (mod n)이면 검증 성공, 아니면 검증 실패
※ ECDSA에 대한 더 자세한 사항들은 SEC1(http://www.secg.org/sec1-v2.pdf)과 ANSI X9.62 표준 및 관련 문서들을 참고하시오.
※ 주의사항 ※
1. 첨부된 프로그램들은 ECDSA 도메인 파라미터가 기록된 param.txt 파일이 실행파일과 같은 경로에 있어야 올바로 실행된다.
2. param.txt에 있는 a, b 또는 G 값들을 변경할 수 있다. G를 변경하는 답안 또는 G를 변경하지 않고 a, b만 변경하는 답안이 가능하다. 단, G를 변경하지 않는 답안이 놓은 점수를 받게 된다.
3. 생성점 G는 압축된 좌표형(y 좌표가 짝수이면 [02||x 좌표], y 좌표가 홀수이면 [03||x 좌표]로 표기)으로 표기되어 있다.
4. 입력되는 16진 스트링(a, b 또는 G 값)은 전체 자리수가 항상 짝수여야 한다. 예를 들어, F23이 아니라 0F23과 같이 입력한다.
5. 실행파일을 보는 것은 허용되지만, 변경해서는 안 된다.
6. 암호학적 사유 없이 프로그램의 오류 등을 통해 얻은 결과들은 무효로 처리한다.
2. 풀이 [목차]
이 풀이를 읽기 전에 문제 02번 풀이를 참고하길 바란다.
signer.exe를 실행시키고 동적 분석을 한 결과 다음 상수값을 발견할 수 있었다.
p = DB7C2ABF62E35E668076BEAD208B16
n = DB7C2ABF62E35E7628DFAC6561C516
그런데 verifier.exe를 실행하고 동적 분석을 하자 더 많은 상수값들이 관찰됐다.
Q = 035A3A2F05FD136C4A58331A648C7216
p = DB7C2ABF62E35E668076BEAD208B16
n = DB7C2ABF62E35E7628DFAC6561C516
a = DB7C2ABF62E35E668076BEAD208816
b = 659EF8BA043916EEDE8911702B2216
G = 0209487239995A5EE76B55F9C2F09816
이를 통해 얻을 수 있는 결론은 첫째로 문제에서 언급되지 않은 public key인 Q가 발견됐다는 점이다. 둘째로, signer.exe는 Q = d G로 정의되는, 서명을 생성하는 데 필요한 파라미터 d 를 저장하고 있지 않다는 점이다. 이는 사용자가 입력해 주어야 할 값일 것이며 Signing key에서 적어야 할 것이다. (필자는 signer.exe에서 Signing key가 무엇을 의미하는 건지 많이 헤맸다.)
한편 왜 주어진 방법대로 하면 검증이 되는지 직관적이지 않다. 따라서 직접 증명할 필요가 있다.
x(u1G + u2Q)
= x(hs -1G + rs -1Q) (*)
= x(hs -1G + rs -1dG) (**)
= x((hs -1 + rs -1d)G)
= x((hs -1 + rds -1)G)
= x((h + rd) s -1G)
= x((h + rd)(k -1(h + dr))-1G) (*)
= x((h + rd)(h + dr)-1kG)
= x(kG)
≡ r (mod n)
이렇게 주어진 검증 방법이 타당함을 보였다. 이제 주어진 문제를 곱씹어 보면 뭔가 위화감이 든다. 필자가 해야하는 일은 verifier.exe가 "!Congratulation~ You did it!"이라는 메시지를 출력하도록 하는 것이다. 그런데, 서명 생성에 필요한 d, m과 서명 검증에 필요한 m, r, s 모두 공유하고 있으므로 당연히 검증에 성공해야 할 것 같다. 그런데 왜 검증은 자꾸 실패하는 걸까?
위 증명을 다시 쳐다보면 간과한 두 개의 사실이 있음을 알 수 있다. 우선 함수 f 가 관여하는 조건 중 G의 위수가 n이라는 점이 있었는데, a, b 값을 아무렇게나 정하면 그 조건이 성립하지 않을 가능성이 높다. 실제로 증명과정에서 (*)로 마크한 부분이 n이 G의 위수라는 조건이 요구되었다. 또한 Signing key에서 넘겨 준 d의 값은 평소처럼 어떤 패스워드를 지정하라는 의미가 아니라 어떤 정확한 값이어야 했던 것이다. 이는 증명과정 중 (**)에서 발견할 수 있으며 Q의 값이 고정돼 있는 상황이기 때문에 발생하는 현상이다.
그렇다면 이제 필자의 목표는 G의 위수가 n이 되도록 Q = dG인 d를 찾을 수 있도록 a, b, G의 값을 바꾸는 것이다. 당장 생각나는 방법은 a, b 값이 정해졌을 때 G의 위수가 n인지 검증해 보는 것으로 그러려면 n·G의 계산이 선행되어야 한다. 하지만 타원곡선에서 덧셈은 좀 특이하게 정의되는데, 각 계산과정이 단순하지는 않다. (즉, n이 굉장히 큰데, 그 덧셈을 일일히 해볼 수는 없는 노릇이다.)
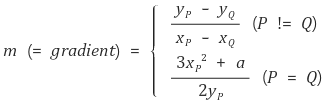
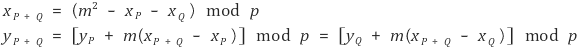
그런데 double and add 알고리즘으로 log n의 시간복잡도로 n·G를 계산할 수 있다.
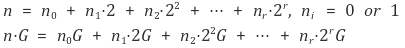
따라서 다음과 같은 알고리즘으로 계산하면 112번의 반복계산으로 n·G를 계산할 수 있다.
nG = 0;
for (i = 0 ; i < 112; i ++){
nG += (int)(n % 2) * G;
nG %= p;
n /= 2;
doubling(G);
}
이때 2 k + 2 k= 2 k+1임을 이용했다.
그런데 각 a, b의 값에 따라 G의 위수가 n인지 확인하는 방법이 과연 타당한지 검증할 필요가 있다. 즉, 이런 식으로 하면 얼마나 오랫동안 컴퓨팅을 해야 할까? n·G의 나머지의 종류는 0부터 p - 1까지 총 p개이다. a의 값에 따라 그 나머지가 충분히 무작위적으로 나온다고 가정할 때, a의 값을 p 까지는 살펴 보아야 할 것이다. p의 값은 대략 2112이므로 사실상 이 방법으로는 풀 수 없다. 또한 만약 오랜 시간을 투자해서 이 문제를 푼다고 한들 Q = dG인 d의 값을 구하는데에 또 시간을 쏟아야 할 것이다.
여기서 난관에 봉착하다가 앞서 조사한 상수값을 구글링 해 보았다. 그러자 그 상수값의 세트를 갖는 커브가 이미 잘 연구돼 있는 "SECP112R1"라는 것을 알 수 있었다. 따라서 초기값으로 주어진 값들이 이미 첫 번째 문제인 nG = O를 만족하고 있다는 것을 알 수 있었다. 그러자 Q = dG, d ∈ ℕ으로부터 다음 명제를 유도했다.
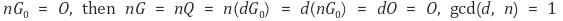
이렇게 두 번째 문제도 해결했으므로 a, b의 값은 건들지 말고 G의 값만 Q의 값으로 바꾸면 충분히 서명 검증을 통과할 것 같다. (참고로 이 경우 d = 1) 정말로 그런지 확인해 보자 결과는 성공적이었다!
a = DB7C2ABF62E35E668076BEAD208816
b = 659EF8BA043916EEDE8911702B2216
G = 035A3A2F05FD136C4A58331A648C7216
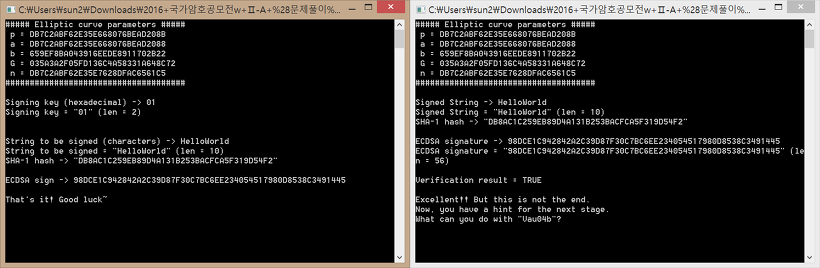
물론 이런 풀이도 맞는 풀이지만 a 또는 b의 값만 바꾸는 방법이 존재하는 듯하다. 아예 어떤 상수도 구하지 않은 채 Q = dG를 구할 수도 있겠지만 이는 전형적인 '어려운' 문제임은 익히 알고 있다. 아마 이 방법이 아닌 "Vau04b"와 관련 있는 다른 풀이가 있어 보인다. 추가적인 조사를 해 보는 과정에서 curve의 order와 어떤 생성점의 order의 관계식이 있고, curve의 order는 어떤 함수식을 갖는다는 것을 알았다. 하지만 필자는 타원곡선에 대해 아는 게 너무 적어 더이상의 풀이를 나중으로 미룬다.
입력: 2016.08.24 00:51
'▶ 자연과학 > ▷ 암호·보안' 카테고리의 다른 글
| 【암호】 이집트 문자 해독 (3) | 2019.08.11 |
|---|---|
| 【보안】 보안 일반 (0) | 2017.10.13 |
| 【국가암호공모전】 (II-A 분야) 문제 06 - 2부 (2016) (0) | 2016.08.15 |
| 【국가암호공모전】 (II-A 분야) 문제 06 - 1부 (2016) (3) | 2016.08.15 |
| 【국가암호공모전】 (II-A 분야) 문제 05 (2016) (5) | 2016.08.14 |



최근댓글