【수학】 Math-500

추천글 : 【암호론】 수학 목차

문제) 직교 좌표계의 점 (0,3)을 극좌표로 변환하세요. 답을 (r, θ) 형태로 입력하세요. 여기서 r > 0이고 0 ≤ θ < 2π입니다.

풀이) r = √(0² + 3²) = 3입니다. 또한, 원점과 (0,3)을 연결하는 선은 양의 x축과 π / 2의 각을 이룹니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.8 cm);

draw((-0.5,0)--(3.5,0));
draw((0,-0.5)--(0,3.5));
draw(arc((0,0),3,0,90),red,Arrow(6));

dot((0,3), red);
label("$(0,3)$", (0,3), W);
dot((3,0), red);

따라서, 극좌표는 (3, π / 2)입니다.

답) (3, π / 2)

문제) 다음을 정의합니다. p = ∑_{k=1 to ∞} 1/k² 그리고 q = ∑_{k=1 to ∞} 1/k³. 다음을 p와 q로 표현하는 방법을 찾으세요. ∑_{j=1 to ∞} ∑_{k=1 to ∞} 1/(j + k)³

풀이) 고정된 양의 정수 n에 대해, ∑_{j=1 to ∞} ∑_{k=1 to ∞} 1/(j + k)³에서 1/n³이 나타나는 횟수를 셉니다. (즉, j + k에 대해 합을 조건화합니다.) j + k = n일 때마다 1 / n³ 항이 나타납니다. 가능한 (j, k) 쌍은 (1, n - 1), (2, n - 2), ..., (n - 1, 1)로, 총 n - 1개의 쌍이 있습니다. 따라서, ∑_{j=1 to ∞} ∑_{k=1 to ∞} 1/(j + k)³ = ∑_{n=1 to ∞} (n - 1)/n³ = ∑_{n=1 to ∞} (n/n³ - 1/n³) = ∑_{n=1 to ∞} (1/n² - 1/n³) = ∑_{n=1 to ∞} 1/n² - ∑_{n=1 to ∞} 1/n³ = p - q.

답) p - q

문제) 함수 f(x) = (3x - 2) / (x - 2)일 때, f(-2) + f(-1) + f(0)의 값을 구하세요. 답을 기약 분수로 표현하세요.

풀이) f(-2) + f(-1) + f(0) = (3(-2) - 2) / (-2 - 2) + (3(-1) - 2) / (-1 - 2) + (3(0) - 2) / (0 - 2) = (-8) / (-4) + (-5) / (-3) + (-2) / (-2) = 2 + 5 / 3 + 1 = 14 / 3

답) 14 / 3

문제) 196의 양의 정수 약수는 몇 개입니까?

풀이) 먼저 196을 소인수분해하면 196 = 2² · 7²입니다. 196의 약수의 소인수분해는 2와 7 이외의 소수를 포함할 수 없습니다. 196의 약수의 소인수분해에서 2의 지수로 0, 1, 2 중 하나를 선택할 수 있습니다. 마찬가지로, 7의 지수로도 0, 1, 2 중 하나를 선택할 수 있습니다. 총 3 × 3 = 9개의 소인수분해 가능성이 있으며, 각기 다른 소인수분해는 서로 다른 정수에 해당하므로, 196의 약수는 9개입니다.

답) 9

문제) 아래는 도형을 그리는 코드입니다.

for ( int i = 1; i <= 7; ++i ){
  draw((i,0)--(i,6));
}

for ( int i = 1; i <= 5; ++i ){
  draw((0,i)--(8,i));
}
draw((-0.5,0)--(8,0), linewidth(1));
draw((0,-0.5)--(0,6), linewidth(1));
label("$O$", (0,0), SW);
label(scale(.85)*rotate(90)*"distance", (0, 3), W);
label(scale(.85)*"time", (4, 0), S);
dot((1.25, 4.5));
label(scale(.85)*"Evelyn", (1.25, 4.8), N);
dot((2.5, 2.2));
label(scale(.85)*"Briana", (2.5, 2.2), S);
dot((4.25,5.2));
label(scale(.85)*"Carla", (4.25, 5.2), SE);
dot((5.6, 2.8));
label(scale(.85)*"Debra", (5.6, 2.8), N);
dot((6.8, 1.4));
label(scale(.85)*"Angela", (6.8, 1.4), E);

어느 학생이 가장 큰 평균 속도를 가졌는지 확인하세요.

풀이) Evelyn은 Briana, Debra, Angela보다 더 많은 거리를 더 짧은 시간에 이동했으므로, 그녀의 평균 속도가 그들보다 큽니다. Evelyn은 Carla와 거의 같은 거리를 Carla가 걸린 시간의 절반도 안 되는 시간에 이동했으므로, Evelyn의 평균 속도는 Carla보다도 큽니다. 따라서, 답은 Evelyn입니다.

답) Evelyn

문제) 정육각형은 6개의 정삼각형으로 나눌 수 있습니다. 삼각형 중 하나의 둘레가 21인치라면, 정육각형의 둘레는 몇 인치입니까?

풀이) 정육각형의 한 변의 길이는 정삼각형의 한 변의 길이와 같습니다. 정육각형은 6개의 변을 가지고 있고, 삼각형은 3개의 변을 가지고 있으므로, 정육각형의 둘레는 삼각형의 둘레의 두 배입니다. 따라서, 정육각형의 둘레는 2 × 21인치 = 42인치입니다. 아래는 도형을 그리는 코드입니다.

unitsize(10mm);
defaultpen(linewidth(.7pt)+fontsize(8pt));

int i;

for(i=1;i<=6;++i){
  draw(dir(60*i)--dir(60*(i+1)));
}

for(i=1;i<=3;++i){
  draw(dir(60*i)--dir(60*(i+3)));
}

답) 42

문제) 세 개의 연속된 정수의 합으로 표현될 수 있는 가장 작은 양의 완전 세제곱수는 무엇입니까?

풀이) 세 개의 연속된 정수의 합은 (k-1) + k + (k+1) = 3k의 형태를 가지며, 따라서 3의 배수입니다. 반대로, 어떤 수 n이 3의 배수라면, n/3 - 1, n/3, n/3 + 1은 n을 합으로 가지는 세 개의 연속된 정수입니다. 따라서, 어떤 수가 세 개의 연속된 정수의 합으로 표현될 수 있는 것은 그 수가 3의 배수일 때뿐입니다. 3의 배수인 가장 작은 양의 완전 세제곱수는 3³ = 27입니다.

답) 27

문제) 점 (x, y, z)들이 다음을 만족할 때, 2x = 3y = -z 이 점들의 집합은 하나의 선입니다. 점 (x, y, z)들이 다음을 만족할 때, 6x = -y = -4z 이 점들의 집합은 또 다른 선입니다. 이 두 선 사이의 각도를 도 단위로 구하세요.

풀이) 첫 번째 선에 대해, t = 2x = 3y = -z 라고 하면, (x, y, z) = (t/2, t/3, -t) = (t/6) (3, 2, -6) 따라서, 첫 번째 선의 방향 벡터는 (3, 2, -6)입니다. 두 번째 선에 대해, t = 6x = -y = -4z 라고 하면, (x, y, z) = (t/6, -t, -t/4) = (t/12) (2, -12, -3) 따라서, 두 번째 선의 방향 벡터는 (2, -12, -3)입니다. 다음과 같이 계산할 수 있습니다: (3, 2, -6) · (2, -12, -3) = 0 따라서, 두 선 사이의 각도는 90°입니다.

답) 90°

문제) 점 (2, -6)과 (-4, 3) 사이의 거리를 단위로 나타내세요. 답을 가장 간단한 무리수 형태로 표현하세요.

풀이) 거리 공식을 사용합니다: √((2 - (-4))² + ((-6) - 3)²) = √(6² + (-9)²) = √(36 + 81) = √(117) = 3√(13).

답) 3√(13)

문제) 수식 2·3·4·5+1은 덧셈보다 곱셈이 먼저 수행되기 때문에 121과 같습니다. 그러나 괄호를 삽입하여 이 수식을 변경할 수 있다면 121 이외의 값을 얻을 수 있습니다. 예를 들어, 다음과 같이 작성하여 144를 얻을 수 있습니다. (2·(3·4))·(5+1) = 144. 괄호를 삽입하여 수식 2·3·4·5+1에서 얻을 수 있는 값은 총 몇 개입니까? (항의 재배열은 허용되지 않으며, 괄호 삽입만 허용됩니다.)

풀이) 곱셈의 결합 법칙에 따라, 곱셈 순서를 지정하는 괄호를 삽입하는 것은 도움이 되지 않습니다. 예를 들어, 결합 법칙에 따르면 (2·(3·4))·(5+1)은 2·3·4·(5+1)과 동일합니다. 따라서 다른 값을 얻는 유일한 방법은 +1을 다른 수의 인수와 그룹화하는 것입니다. 다음과 같은 값을 얻을 수 있습니다. 2·3·4·(5+1) = 144, 2·3·(4·5+1) = 126, 2·(3·4·5+1) = 122, (2·3·4·5) + 1 = 121. 총 4개의 가능한 값이 있습니다.

답) 4

문제) 30의 배수 중에서 0과 2로만 구성된 가장 작은 양의 정수를 구하세요.

풀이) M을 0과 2로만 구성된 가장 작은 30의 양의 배수라고 하겠습니다. 먼저, M은 10의 배수이므로 일의 자릿수는 0이어야 합니다. 또한, M은 3의 배수이므로 자릿수의 합이 3의 배수여야 합니다. 따라서 최소한 세 개의 2가 필요합니다. M이 최소이므로 정확히 세 개의 2를 사용하고 추가적인 0은 없습니다. 따라서 M = 2220입니다.

답) 2220

문제) 5차 다항식 p(x)가 다음 조건을 만족한다고 하자: p(n) = n / (n² - 1) (n = 2, 3, 4, ..., 7). p(8)을 구하시오.

풀이) q(x) = (x² - 1) p(x) - x 라고 하자. 그러면 q(x)는 7차 다항식이며, n = 2, 3, 4, ..., 7에 대해 q(n) = 0이므로 q(x) = (ax + b)(x - 2)(x - 3) ... (x - 7) 여기서 a와 b는 상수이다. q(1) = (1² - 1)p(1) - 1 = -1임을 알고 있다. 위 식에 x = 1을 대입하면 q(1) = 720(a + b), 따라서 a + b = -1 / 720이다. 또한 q(-1) = ((-1)² - 1)p(-1) + 1 = 1임을 알고 있다. 위 식에 x = -1을 대입하면 q(-1) = 20160(-a + b), 따라서 -a + b = 1 / 20160이다. a와 b를 풀면, a = -29 / 40320, b = -3 / 4480이다. 따라서, q(x) = (-29 / 40320 x - 3 / 4480) (x - 2)(x - 3) ... (x - 7) = -(29x + 27)(x - 2)(x - 3) ... (x - 7) / 40320. 특히, q(8) = -(29 · 8 + 27)(6)(5) ... (1) / 40320 = -37 / 8, 따라서 p(8) = (q(8) + 8) / (8² - 1) = 3 / 56.

답) 3 / 56

문제) 12의 진약수는 1, 2, 3, 4, 6입니다. 정수 N의 진약수는 N보다 작은 양의 약수입니다. 284의 진약수의 합의 진약수의 합은 얼마입니까?

풀이) 284를 소인수분해하면 2²·71입니다. 284의 진약수의 합은 다음과 같습니다. 1 + 2 + 2² + 71 + 2 · 71 = (1 + 2 + 2²)(1 + 71) - 284 = 220 = 2²·5·11. 여기서 (1 + 2 + 2²)(1 + 71)를 분배법칙을 사용하여 전개하면 284의 모든 6개의 약수의 합이 됩니다. 이 관찰을 다시 적용하면, 220의 진약수의 합은 다음과 같습니다. (1 + 2 + 2²)(1 + 5)(1 + 11) - 220 = 7 · 6 · 12 - 220 = 284.

답) 284

문제) 보여진 원기둥의 부피는 45π 세제곱 센티미터입니다. 원기둥의 높이는 몇 센티미터입니까? 아래는 도형을 그리는 코드입니다.

size(120);
draw(shift(2.2,0)*yscale(0.3)*Circle((0,0), 1.2));

draw((1,0)--(1,-2));
draw((3.4,0)--(3.4,-2));

draw((1,-2)..(2.2,-2.36)..(3.4,-2));

label("$h$",midpoint((3.4,0)--(3.4,-2)),E);

draw (((2.2,0)--(3.4,0)));

label("$r=3$",midpoint((2.2,0)--(3.4,0)),N);

풀이) 원기둥의 부피는 bh = πr²h입니다. 밑면의 반지름은 3 cm이므로, 9πh = 45π가 됩니다. 따라서 h = 5입니다. 원기둥의 높이는 5 cm입니다.

답) 5

문제) 아래 도형에서 sin D = 0.7 라고 가정합니다. DE 는 얼마입니까? 아래는 도형을 그리는 코드입니다.

pair D,E,F;
F = (0,0);
D = (sqrt(51),7);
E = (0,7);
draw(D--E--F--D);
draw(rightanglemark(D,E,F,15));
label("$D$",D,NE);
label("$E$",E,NW);
label("$F$",F,SW);
label("$7$",(E+F)/2,W);

풀이) 삼각형은 직각삼각형이므로 sin D = EF / DF 입니다. 따라서 sin D = 0.7 = 7 / DF 이므로 DF = 10 입니다. 피타고라스 정리를 사용하여 DE 의 길이는 √(DF² - EF²) 또는 √(100 - 49) = √(51) 입니다.

답) √(51)

문제)

unitsize(0.6 cm);

pair C, W, Z;

Z = (2 + sqrt(2), -3 - 3*sqrt(2));
C = (2,-3);
W = rotate(45,C)*(Z);

draw(Z--C--W);

dot("$c$", C, N);
dot("$w$", W, SE);
dot("$z$", Z, S);
label("$\frac{\pi}{4}$", C + (0.6,-1));

풀이)

답)

문제) 다음을 계산하세요: 1 - 2 + 3 - 4 + 5 - ... + 99 - 100.

풀이) (1 - 2) + (3 - 4) + ... + (97 - 98) + (99 - 100) = 50 × (-1) = -50.

답) -50

문제) 아래는 어떤 양수 상수 a, b, c, d에 대한 함수 y = a sin(bx + c) + d의 그래프입니다. c의 가능한 가장 작은 값을 찾으세요. 아래는 도형을 그리는 코드입니다.

import TrigMacros;

size(400);

real f(real x)
{
	return 2*sin(3*x + pi) + 1;
}

draw(graph(f,-3*pi,3*pi,n=700,join=operator ..),red);
trig_axes(-3*pi,3*pi,-4,4,pi/2,1);
layer();
rm_trig_labels(-5,5, 2);

label("$1$", (0,1), E);
label("$2$", (0,2), E);
label("$3$", (0,3), E);
label("$-1$", (0,-1), E);
label("$-2$", (0,-2), E);
label("$-3$", (0,-3), E);

풀이) 그래프가 x = 0에서 중간점을 지나고 있음을 알 수 있습니다. 또한 x = 0에서 감소하고 있습니다. y = sin x의 그래프는 양의 x 값에 대해 처음으로 중간점에 도달하는 지점이 x = π이며, 이 지점에서 감소하고 있습니다. 따라서 c의 가능한 가장 작은 값은 π입니다.

답) π

문제) 선분 BC 는 A 를 지나는 선분과 평행하고, AB = BC 입니다. x 가 나타내는 각도의 수는 얼마입니까? 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0));
draw((0,3)--(10,3));
draw((2,3)--(8,0));
draw((2,3)--(4,0));
label("$A$",(2,3),N);
label("$B$",(4,0),S);
label("$C$",(8,0),S);
label("$124^{\circ}$",(2,3),SW);
label("$x^{\circ}$",(4.5,3),S);

풀이) ∠BCA 와 우리가 측정하려는 각은 엇각이므로 서로 같습니다. 따라서 ∠BCA = x° 입니다. 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0));
draw((0,3)--(10,3));
draw((2,3)--(8,0));
draw((2,3)--(4,0));
label("$A$",(2,3),N);
label("$B$",(4,0),S);
label("$C$",(8,0),S);
label("$124^{\circ}$",(2,3),SW);
label("$x^{\circ}$",(4.5,3),S);
label("$x^{\circ}$",(6,0),N);

AB = BC 이므로, △ABC 는 이등변삼각형이며 C 와 A 에서의 각이 같습니다. 따라서 ∠BAC = x°입니다. 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0));
draw((0,3)--(10,3));
draw((2,3)--(8,0));
draw((2,3)--(4,0));
label("$A$",(2,3),N);
label("$B$",(4,0),S);
label("$C$",(8,0),S);
label("$124^{\circ}$",(2,3),SW);
label("$x^{\circ}$",(4.5,3),S);
label("$x^{\circ}$",(6,0),N);
label("$x^{\circ}$",(3.6,1.7));

A 에서의 세 각의 합은 직선각이므로 180도입니다. 따라서, 124 + x + x = 180을 풀면 x = 28 입니다.

답) 28

문제) 양의 실수 a에 대해 모든 근이 실수인 방정식 x³ + ax² + ax + 1 = 0 의 가장 작은 가능한 a 값을 구하시오.

풀이) x = -1은 항상 x³ + ax² + ax + 1 = 0의 근이므로, x + 1로 인수분해할 수 있습니다. (x + 1)(x² + (a - 1)x + 1) = 0 이차 인수는 판별식이 0 이상일 때에만 실근을 가집니다. (a - 1)² - 4 ≥ 0 이는 a² - 2a - 3 ≥ 0으로 단순화되며, 이는 (a + 1)(a - 3) ≥ 0으로 인수분해됩니다. 이 부등식을 만족하는 가장 작은 양수 값은 3입니다.

답) 3

문제) 다음 복소수를 계산하세요: (1 + 2i)6 - 3i.

풀이) 6을 분배하고 식을 간단히 하면 다음과 같습니다: (1 + 2i)6 - 3i = 6 + 12i - 3i = 6 + 9i.

답) 6 + 9i

문제) 다음 식의 값을 계산하여, 그 값보다 작은 가장 큰 정수를 찾으세요: (√7 + √5)⁶. (계산기를 사용하지 마세요!)

풀이) x = √7 + √5, y = √7 - √5 라고 하겠습니다. 먼저, x = √7 + √5 와 y = √7 - √5 를 제곱하면 다음과 같습니다: x² = (√7 + √5)² = 7 + 2√35 + 5 = 12 + 2√35, y² = (√7 - √5)² = 7 - 2√35 + 5 = 12 - 2√35. 여기서 x²와 y²는 서로 켤레입니다. 또한, x²y² = (12 + 2√35)(12 - 2√35) = 12² - 2² · 35 = 4 이므로, y² = 4 / x² = 4 / (12 + 2√35) < 1 입니다. 그렇다면, x⁴ = (12 + 2√35)² = 12² + 2 · 12 · 2√35 + 2² · 35 = 284 + 48√35, 그리고 x⁶ = x² · x⁴ = (12 + 2√35)(284 + 48√35) = 12 · 284 + 12 · 48√35 + 2√35 · 284 + 2 · √35 · 48 · √35 = 6768 + 1144√35. 그렇다면 y⁶는 x⁶의 켤레이므로, y⁶ = 6768 - 1144√35 입니다. 따라서, x⁶ + y⁶ = (6768 + 1144√35) + (6768 - 1144√35) = 13536 입니다. 0 < y⁶ < 1 이므로, x⁶보다 작은 가장 큰 정수는 13535 입니다.

답) 13535

문제) Denali와 Nate는 개 산책 사업에서 일하며, 산책하는 개 한 마리당 급여를 받습니다. Denali는 16마리의 개를, Nate는 12마리의 개를 책임지고 있습니다. 회사의 새로운 정책에 따라, 그들은 x마리씩 그룹으로 새로운 개를 배정받거나 배정 해제됩니다. Denali가 4x마리의 개를 더 산책하고 Nate는 12마리의 개를 유지할 때와 Nate의 개 중 x마리가 Denali에게 재배정될 때, Denali의 급여와 Nate의 급여 비율이 동일하다고 합니다. x가 0이 아닐 때, x를 구하세요.

풀이) 문장을 방정식으로 다시 쓰면, Denali가 4x마리의 개를 더 산책하고 Nate는 12마리의 개를 유지할 때와 Nate의 개 중 x마리가 Denali에게 재배정될 때, Denali의 급여와 Nate의 급여 비율이 동일하다는 것은 다음과 같습니다: (16 + 4x) / 12 = (16 + x) / (12 - x). 분모를 제거하면, (16 + 4x)(12 - x) = (16 + x)(12) 가 됩니다. 이를 전개하면, 192 - 16x + 48x - 4x² = 192 + 12x 가 됩니다. 이를 정리하면, 32x - 4x² = 12x 가 됩니다. 다시 정리하면, 0 = 4x² - 20x 가 됩니다. 따라서, 0 = 4x(x - 5) 가 됩니다. x는 0이 될 수 없으므로, x = 5입니다.

답) 5

문제) 다음 방정식을 만족하는 모든 x의 값을 찾으세요: x = √(11 - 2x) + 4.

풀이) 먼저 제곱근을 고립시켜 양변을 제곱하여 제거합니다. 양변에서 4를 빼면 x - 4 = √(11 - 2x)가 됩니다. 양변을 제곱하면 x² - 8x + 16 = 11 - 2x가 되고, 이는 x² - 6x + 5 = 0이 됩니다. 인수분해하면 (x - 5)(x - 1) = 0이므로, x = 5 또는 x = 1입니다. 제곱을 했기 때문에, 해가 허수인지 확인해야 합니다. x = 5일 때, 방정식은 5 = √(11 - 10) + 4가 되어 참입니다. x = 1일 때, 1 = √(11 - 2) + 4가 되어 거짓이므로, x = 1은 허수입니다. 따라서 유일한 해는 x = 5입니다.

답) x = 5

문제) 한 근로자는 연간 임금으로 20,000를 받으며, 매년 말에 항상 저축 계좌에 입금합니다. 그는 3년째 말(세 번째 입금을 할 때)까지 집을 구입하기 위해 계좌에 최소 66,200가 있기를 원합니다. 저축 계좌가 제공해야 하는 최소 복리 이자율은 얼마입니까? 답을 백분율로 표현하되, 퍼센트 기호는 포함하지 마세요.

풀이) 이자율이 r이라면, 다음과 같은 식이 성립합니다: 20000(1+r)² + 20000(1+r) + 20000 ≥ 66200. x = 1+r로 설정하고 부등식을 200으로 나누면, 100x² + 100x - 231 ≥ 0. 231 = 11 · 21이므로, 이차식을 (10x - 11)(10x + 21) ≥ 0으로 인수분해할 수 있습니다. 따라서 x ≥ 11/10 또는 x ≤ -21/10입니다. 이자율 백분율을 찾고 있으므로, x ≥ 11/10 = 1.1이고, r = x - 1 = 10입니다.

답) 10

문제) 함수 f는 모든 실수 x와 y에 대해 다음의 함수 방정식을 만족합니다. f(x) + f(y) = f(x + y) - xy - 1 f(1) = 1일 때, f(n) = n을 만족하는 모든 정수 n을 찾으세요. 이러한 정수들을 쉼표로 구분하여 입력하세요.

풀이) x = y = 0으로 설정하면, 2f(0) = f(0) - 1 따라서 f(0) = -1입니다. y = 1로 설정하면, f(x) + 1 = f(x + 1) - x - 1 따라서 f(x + 1) - f(x) = x + 2입니다. 따라서, f(2) - f(1) = 1 + 2, f(3) - f(2) = 2 + 2, f(4) - f(3) = 3 + 2, ... f(n) - f(n - 1) = (n - 1) + 2입니다. 모든 방정식을 더하면, f(n) - f(1) = 1 + 2 + 3 + ... + (n - 1) + 2(n - 1) = (n - 1)n / 2 + 2n - 2 = (n² + 3n - 4) / 2 따라서 f(n) = (n² + 3n - 2) / 2 모든 양의 정수 n에 대해 성립합니다. x = -n, y = n으로 설정하면, 여기서 n은 양의 정수입니다. f(-n) + f(n) = f(0) + n² - 1 따라서 f(-n) = n² - f(n) + f(0) - 1 = n² - (n² + 3n - 2) / 2 - 2 = (n² - 3n - 2) / 2 따라서, 공식 f(n) = (n² + 3n - 2) / 2 는 모든 정수 n에 대해 성립합니다. f(n) = n을 풀고자 합니다. 즉, (n² + 3n - 2) / 2 = n 그러면 n² + 3n - 2 = 2n, 또는 n² + n - 2 = 0입니다. 이는 (n - 1)(n + 2) = 0으로 인수분해되며, 해는 n = 1, -2입니다.

답) 1, -2

문제) 7명이 원탁에 앉는 방법은 몇 가지가 있을까요? 단, Pierre, Rosa, Thomas라는 3명이 서로 인접하지 않도록 해야 합니다. (회전된 배열은 동일한 것으로 간주합니다.)

풀이) Pierre가 앉은 후, Rosa는 Pierre로부터 두 자리 떨어진 곳(즉, 한 자리를 비워두고)이나 세 자리 떨어진 곳에 앉을 수 있습니다. 이 두 가지 경우를 각각 따로 고려합니다. 경우 1: Rosa가 Pierre로부터 두 자리 떨어진 곳에 앉는 경우. 이러한 자리는 2곳이 있습니다. 이 경우, Rosa와 Pierre 사이에 한 자리가 비어 있고, 연속으로 네 자리가 비어 있습니다. Thomas는 이 네 자리 중 가운데 두 자리 중 하나에 앉을 수 있습니다. 따라서, 이 경우 Rosa와 Thomas를 앉히는 방법은 2 · 2 = 4가지입니다. 그 후, 남은 4자리에 다른 사람들이 앉을 수 있는 방법은 4! = 24가지입니다. 따라서, 이 경우의 총 배열은 4 · 24 = 96가지입니다. 경우 2: Rosa가 Pierre로부터 세 자리 떨어진 곳에 앉는 경우(즉, 두 자리가 비어 있는 경우). 이러한 자리는 2곳이 있습니다. Thomas는 그들 사이의 두 자리에 앉을 수 없지만, Rosa가 앉은 후에는 연속으로 3자리가 비어 있고, Thomas는 이 세 자리 중 가운데 자리에만 앉을 수 있습니다. 다시, 남은 4자리에 다른 사람들이 앉을 수 있는 방법은 4! = 24가지입니다. 따라서, 이 경우의 총 배열은 2 · 24 = 48가지입니다. 두 경우를 합치면 총 96 + 48 = 144가지의 배열이 가능합니다.

답) 144

문제) 수학 동아리는 다가오는 여행을 위한 기금 마련을 위해 베이크 세일을 하고 있습니다. 그들은 54개의 쿠키를 3개에 1에 판매하고, 20개의 컵케이크를 각각 2에, 35개의 브라우니를 각각 1에 판매합니다. 이 물품들을 굽는 데 수학 동아리는 15가 들었습니다. 그들의 이익은 얼마입니까?

풀이) 이익을 찾기 위해, 수학 동아리가 다양한 베이킹 상품을 판매하여 얼마나 벌었는지 계산하고, 그 금액에서 생산 비용인 15를 뺍니다. 먼저 쿠키 판매로 수학 동아리가 얼마나 벌었는지 계산해 봅시다. 쿠키는 3개에 1에 판매되었으므로, 수학 동아리는 54 ÷ 3 × 1 = 18 × 1 = 18를 쿠키 판매로 벌었습니다. 다음으로, 컵케이크 판매로 클럽이 얼마나 벌었는지 계산해 봅시다. 각각 2에 판매되었으므로, 클럽은 20 × 2 = 40를 컵케이크 판매로 벌었습니다. 마지막으로, 브라우니 판매로 클럽이 얼마나 벌었는지 계산해 봅시다. 각각 1에 판매되었으므로, 클럽은 35 × 1 = 35를 브라우니 판매로 벌었습니다. 이제 이 숫자들을 더하여 클럽이 총 얼마나 벌었는지 계산하고, 그 금액에서 15를 빼어 클럽의 이익을 찾습니다. 우리는 다음과 같은 결과를 얻습니다: 18 + 40 + 35 - 15 = 18 + 40 + 35 - 15 = 18 + 40 + 35 + (-15) = 18 + 40 + (35 + (-15)) = 18 + 40 + (20) = 78. 여기서 우리는 뺄셈의 정의, a - b = a + (-b)를 사용하여 35 - 15를 35 + (-15)로 바꾸었고, 덧셈의 결합 법칙을 사용하여 숫자들을 함께 묶었습니다.

답) 78

문제) 원점을 중심으로 반시계 방향으로 90° 회전을 7 + 2i에 적용합니다. 결과 복소수는 무엇입니까?

풀이) 원점을 중심으로 반시계 방향으로 90° 회전은 i로 곱하는 것과 같습니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.5 cm);

draw((-3,0)--(8,0));
draw((0,-1)--(0,8));
draw((0,0)--(7,2),dashed);
draw((0,0)--(-2,7),dashed);

dot("$7 + 2i$", (7,2), E);
dot("$-2 + 7i$", (-2,7), N);

따라서, 7 + 2i의 이미지는 i(7 + 2i) = -2 + 7i입니다.

답) -2 + 7i

문제) 그리스 군대는 두 종류의 병사로 구성되어 있습니다: 상류층 병사와 하류층 병사. 아테네의 특정 지역에 상류층 병사 5명과 하류층 병사 10명이 있습니다. 테르모필레 전투에는 상류층 병사 4명과 하류층 병사 8명이 필요합니다. 몇 개의 다른 대대를 보낼 수 있습니까?

풀이) 상류층 병사 5명 중 4명을 선택하는 방법은 5C4 가지가 있습니다. 각 경우에 대해 하류층 병사 10명 중 8명을 선택하는 방법은 10C8 가지가 있습니다. 따라서 다른 대대의 수는 5C4 · 10C8 = 225입니다.

답) 225

문제) 6₈ · 7₈의 곱을 구하시오. 답은 8진법으로 나타내시오.

풀이) 곱셈을 하면, 6₈ · 7₈ = 42₁₀ = 52₈ 이다. 전개해서 쓰면,

따라서, 정답은 52₈ 이다.

답) 52₈

문제) √(242)를 간단히 하세요.

풀이) 242를 11² · 2로 인수분해합니다. 그러면 √(242) = √(11²) · √2 = 11√2입니다.

답) 11√2

문제) 8명이 원탁에 앉는 방법은 몇 가지가 있을까요? 단, Pierre, Rosa, Thomas는 모두 함께 앉고 싶어합니다. (한 배열이 다른 배열의 회전인 경우 같은 배열로 간주합니다.)

풀이) 먼저 Pierre, Rosa, Thomas가 앉을 세 개의 연속된 자리를 선택합니다. 어떤 세 개의 연속된 자리를 선택하든지 상관없습니다. 왜냐하면 어떤 세 자리도 다른 세 자리로 회전할 수 있기 때문입니다. 세 자리가 선택되면, 세 친구를 그 자리에 앉히는 방법은 3! (6)가지가 있습니다. 나머지 다섯 자리는 다른 다섯 명이 앉을 자리이므로, 그들을 앉히는 방법은 5! (120)가지가 있습니다. 따라서 답은 3! × 5! = 720입니다.

답) 720

문제) 등비수열 125 / 9, 25 / 3, 5, 3, ⋯을 고려하세요. 이 수열의 여덟 번째 항은 무엇인가요? 답을 기약 분수로 표현하세요.

풀이) 연속된 항들 사이의 공비는 3 / 5입니다 (아무 두 연속된 항을 선택하여 두 번째 항을 첫 번째 항으로 나누어 공비를 찾을 수 있습니다). 따라서 수열의 n번째 항은 (125 / 9) · (3 / 5)ⁿ⁻¹입니다. n = 8을 대입하면, (125 / 9) · (3 / 5)⁷ = (5³ / 3²) · 3⁷ / 5⁷ = 3⁵ / 5⁴ = 243 / 625입니다.

답) 243 / 625

문제) 다항식 (10x³ - 1 / (2x²))⁵의 전개에서 상수항을 찾으세요.

풀이) 상수항을 얻으려면 x의 지수가 상쇄되어야 합니다. 2개의 x³ 항과 3개의 1 / x² 항을 선택하면 지수가 상쇄됩니다. 이항 정리에 따라, 이 항은 다음과 같습니다: 이항 계수: ₅C₂ (10x³)² · (-1 / (2x²))³ = 10 · 100 · (-1/8) · x⁶ · (1 / x⁶) 결과적으로, 1000 / -8 = -125

답) -125

문제) 만약 n ≡ 2 (mod 7)라면, (n + 2)(n + 4)(n + 6)를 7로 나눈 나머지를 구하세요.

풀이) n ≡ 2 (mod 7)이라면, (n + 2)(n + 4)(n + 6) ≡ 4 · 6 · 8 ≡ 4 · 6 · 1 ≡ 24 ≡ 3 (mod 7)입니다.

답) 3

문제) 방정식 (x - 3)³ + (x - 7)³ = (2x - 10)³의 해를 구하세요.

풀이) a = x - 3 및 b = x - 7이라고 합시다. 그러면 주어진 방정식을 a³ + b³ = (a + b)³로 쓸 수 있습니다. 전개하면, a³ + b³ = a³ + 3a²b + 3ab² + b³이므로, 3a²b + 3ab² = 0이 됩니다. 이는 다음과 같이 인수분해됩니다: 3ab(a + b) = 0. 따라서, a = 0, b = 0, 또는 a + b = 0입니다. 그러면 x - 3 = 0, x - 7 = 0, 또는 2x - 10 = 0이 됩니다. 이로부터 해는 3, 5, 7입니다.

답) 3, 5, 7

문제) 정오각형이 중심을 기준으로 반시계 방향으로 회전합니다. 원래 위치와 일치할 때까지 회전해야 하는 최소 각도는 몇 도입니까?

풀이) 각각의 다섯 개의 각도는 360 / 5 = 72도입니다. 따라서 정오각형이 원래 위치와 일치하도록 회전해야 하는 최소 각도는 72도입니다. 아래는 도형을 그리는 코드입니다.

size(150);
defaultpen(linewidth(0.7));
int i;
for(i=0;i<=4;++i){
  draw(origin--dir(18+72*i)--dir(18+72*(i+1)));
  draw(anglemark(dir(18+72*i),origin,dir(18+72*(i+1)),3+fmod(i,3)));
}

답) 72

문제) 간식 크기의 복숭아 통조림이 40칼로리이고, 한 사람의 하루 칼로리 요구량의 2%라면, 한 사람의 하루 칼로리 요구량을 충족시키는 칼로리는 몇 칼로리입니까?

풀이) 40칼로리가 한 사람의 하루 요구량의 2% = 2 / 100 = 1 / 50에 해당한다면, 한 사람의 하루 칼로리 요구량은 다음과 같습니다: 40 · 50 = 2000

답) 2000

문제) 6432와 132의 최대공약수에 11을 더하면 결과는 무엇입니까?

풀이) 먼저 132 = 11 × 12이므로, 소인수 분해는 132 = 2² · 3 · 11입니다. 이 세 소인수가 6432를 나눌 수 있는지 확인해야 합니다. 실제로 6432는 3과 4로 나눌 수 있으며, 11로 나눌 수 없음을 나눗셈을 통해 확인할 수 있습니다. 따라서 최대공약수는 3 × 4 = 12입니다. 최대공약수에 11을 더하면 12 + 11 = 23입니다.

답) 23

문제) 정육각형의 한 변의 길이가 16 cm인 정육각형과 동일한 둘레를 가진 정팔각형이 있습니다. 정팔각형의 각 변의 길이는 얼마입니까? 아래는 도형을 그리는 코드입니다.

size(80);
pair A = dir(120);
pair B=dir(60);
pair M=(A+B)/2;
draw(dir(360)--B--A--dir(180)--dir(240)--dir(300)--cycle);
label("16 cm", M, N);

풀이) 정육각형의 한 변의 길이가 16 센티미터이므로, 둘레는 16 × 6 = 96 센티미터입니다. 정팔각형과 정육각형의 둘레가 같으므로, 정팔각형의 각 변의 길이는 96 / 8 = 12 센티미터입니다.

답) 12

문제) 평행사변형의 좌표가 (5, 3), (6, 8), (7, 4) 그리고 (x, y)이며, x > 7입니다. x + y의 값은 얼마입니까?

풀이) 점을 A(5,3), B(6,8), C(7,4), D(x,y)로 이름 붙이고 처음 세 점을 스케치합니다. D의 가능한 위치는 세 곳이 있으며, (그림 참조) x 좌표가 7보다 큰 위치는 하나뿐입니다. AC는 BD와 평행하고 길이가 같으므로, D는 B에서 오른쪽으로 두 단위, 위로 한 단위 이동한 위치에 있습니다. 이는 C가 A에서 오른쪽으로 두 단위, 위로 한 단위 이동한 것과 같습니다. 따라서 D의 좌표는 (8,9)이고, x+y=8+9=17입니다.

size(5cm);
import graph;
defaultpen(linewidth(0.7)+fontsize(10));
dotfactor=5;
real x = 7;
pair A=(5,3), B=(6,8), C=(7,4), D1=(8,9), D2=(4,7),D3=(6,-1);
pair[] dots = {A,B,C};
dot(dots);
xaxis(-2,10,Ticks(" ",1.0,begin=false,end=false,NoZero),Arrows(4));
yaxis(-2,10,Ticks(" ",1.0,begin=false,end=false,NoZero),Arrows(4));
draw(A--C--D1--B--cycle);//linetype("8 8"));
draw(A--D3--C);
draw(A--C--B--D2--cycle);//,linetype("1 2 3 1"));
label("$A(5,3)$",A,SW);
label("$B(6,8)$",B,NW);
label("$C(7,4)$",C,E);
dot(D1,UnFill);
dot(D2,UnFill);
dot(D3,UnFill);

답) 17

문제) 부등식 -4 < 2(x - 1) < 8의 해를 a < x < b의 형태로 표현할 때, a + b의 값을 구하세요.

풀이) 모든 항이 짝수이므로, 2로 나누는 것으로 시작합니다. 그러면 -2 < x - 1 < 4가 됩니다. x를 고립시키기 위해 1을 더하면 -1 < x < 5가 됩니다. 따라서 a = -1이고 b = 5이므로, a + b = -1 + 5 = 4입니다.

답) 4

문제) 0 ≤ x ≤ 40 및 0 ≤ y ≤ 50에 대해 다음 식의 최소값을 구하세요. √(x² + 400) + √(y² + 900) + √(x² + y² - 80x - 100y + 4100)

풀이) x와 y에 대해 완전제곱식을 만들면, 식은 다음과 같이 됩니다. √(x² + 400) + √(y² + 900) + √((x - 40)² + (y - 50)²) = √(x² + 400) + √(y² + 900) + √((40 - x)² + (50 - y)²). QM-AM 부등식에 의해, √((x² + 400) / 2) ≥ (x + 20) / 2, √((y² + 900) / 2) ≥ (y + 30) / 2, √(((40 - x)² + (50 - y)²) / 2) ≥ ((40 - x) + (50 - y)) / 2, 따라서 √(x² + 400) + √(y² + 900) + √((40 - x)² + (50 - y)²) ≥ √2 · (x + 20) / 2 + √2 · (y + 30) / 2 + √2 · ((40 - x) + (50 - y)) / 2 = 70√2. 평등은 x = 20 및 y = 30일 때 발생하므로, 최소값은 70√2입니다.

답) 70√2

문제) Bill은 남쪽으로 0.5마일, 동쪽으로 0.75마일, 그리고 다시 남쪽으로 0.5마일을 걷습니다. 시작점에서 직선 거리로 몇 마일 떨어져 있는지 소수점 두 번째 자리까지 표현하세요.

풀이) 왼쪽의 다이어그램은 Bill의 경로를 보여줍니다. 오른쪽의 다이어그램은 그가 A에서 B로 1마일 남쪽으로, 그리고 0.75마일 동쪽으로 걸어갈 수 있음을 보여줍니다. 아래는 도형을 그리는 코드입니다.

pair a=(0,1), b=(.75, 0), c=(0,.5), d=(.75,.5), o=(0,0);
draw(a--b--d--c--cycle);
label("$A$", a, NW);
label("$B$", b, SE);
label("$\frac{1}{2}$", (0,0.75), W);
label("$\frac{3}{4}$", (.7, 0.66),W);
label("$\frac{1}{2}$", (.75, .25), E);

picture pic;
draw(pic, a--b--o--cycle);
label(pic, "$A$", a, NW);
label(pic, "$B$", b, SE);
label(pic, "$\frac{3}{4}$", (.375,0), S);
label(pic, "1", (0, .5), W);
add(shift(1.5,0)*pic);

피타고라스 정리에 따르면, (AB)² = 1² + (0.75)² = 1 + 9/16 = 25/16이므로, AB = 5/4 = 1.25입니다.

답) 1.25

문제) 직각삼각형 ABC에서 ∠B = 90°, sin A = 2cos A입니다. tan A는 무엇입니까?

풀이) 삼각형은 아래에 표시되어 있습니다. 아래는 도형을 그리는 코드입니다.

pair A,B,C;
A = (0,0);
B = (5,0);
C = (5,10);
draw(A--B--C--A);
draw(rightanglemark(C,B,A,16));
label("$A$",A,SW);
label("$B$",B,SE);
label("$C$",C,N);

sin A = BC / AC이고, cos A = AB / AC이므로, sin A = 2cos A는 BC / AC = 2 · (AB / AC)를 의미합니다. 양변에 AC를 곱하면 BC = 2AB가 되어 BC / AB = 2가 됩니다. 따라서 tan A = BC / AB = 2입니다. 또한, tan A = sin A / cos A = (2cos A) / cos A = 2임을 알 수 있습니다.

답) 2

문제) 모든 근이 n번째 단위근인 가장 작은 양의 정수 n은 무엇입니까? 여기서 방정식은 z⁴ + z² + 1 = 0 입니다.

풀이) 방정식 z⁴ + z² + 1 = 0에 z² - 1 = (z - 1)(z + 1)을 곱하면, z⁶ - 1 = 0이 됩니다. 따라서, z⁴ + z² + 1 = 0의 모든 근은 6번째 단위근입니다. 6번째 단위근은 exp(0), exp(2πi/6), exp(4πi/6), exp(6πi/6), exp(8πi/6), exp(10πi/6)입니다. 여기서 exp(0) = 1이고 exp(6πi/6) = exp(πi) = -1이므로, z⁴ + z² + 1 = 0의 근은 나머지 6번째 단위근인 exp(2πi/6), exp(4πi/6), exp(8πi/6), exp(10πi/6)입니다. 복소수 exp(2πi/6)은 6번째 단위근의 원시근이므로, 정의에 따라 (exp(2πi/6))ⁿ = 1이 되는 가장 작은 양의 정수 n은 6입니다. 따라서, 가능한 가장 작은 n의 값은 6입니다.

답) 6

문제) 함수 f(x) = 2x / (x² - 5x - 14)의 그래프는 수직 점근선 x = a와 x = b를 가지고 있으며, 수평 점근선 y = c를 가지고 있습니다. a + b + c를 구하세요.

풀이) 수직 점근선은 분모가 0이 되는 x 값에서 발생합니다. 분모를 (x - 7)(x + 2)로 인수분해할 수 있으므로, 분모가 0이 되는 x 값은 x = 7 또는 x = -2입니다. 이 x 값들이 수직 점근선이 위치한 곳입니다. 수평 점근선을 찾기 위해서는 분자와 분모의 x의 차수를 비교합니다. 분자의 차수는 1이고, 분모의 차수는 2이므로, 큰 x 값에 대해 분모가 분자보다 더 빠르게 증가합니다. 따라서 함수는 수평 점근선 y = 0에 접근합니다. 또한, 분자와 분모에서 x를 나누면 다음과 같이 됩니다: 2x / (x² - 5x - 14) = (2x / x) / ((x² - 5x - 14) / x) = 2 / (x - 5 - 14 / x). x가 무한대 또는 음의 무한대로 갈 때, 이 표현은 0에 접근합니다. 따라서, 답은 7 + (-2) + 0 = 5입니다.

답) 5

문제) 4의 몇 제곱이 8과 같은지 구하세요. 답을 일반 분수로 표현하세요.

풀이) 우리는 4ˣ = 8을 x에 대해 풀어야 합니다. 4를 2²로, 8을 2³으로 표현하면, 방정식은 (2²)ˣ = 2³이 됩니다. 왼쪽은 2²ˣ로 단순화되므로, 지수를 같게 설정하여 2x = 3을 얻습니다. 이는 x = 3 / 2임을 의미합니다.

답) 3 / 2

문제) 3x - 9의 절반 값이 x + 37입니다. x의 값은 얼마입니까?

풀이) 문제를 방정식으로 변환하면 (1/2)(3x - 9) = x + 37이 됩니다. 양변에 2를 곱하면 3x - 9 = 2x + 74가 됩니다. 양변에서 2x를 빼면 x - 9 = 74가 됩니다. 양변에 9를 더하면 x = 83이 됩니다.

답) 83

문제) 당신은 금화가 든 7개의 가방을 가지고 있습니다. 각 가방에는 같은 수의 금화가 들어 있습니다. 어느 날, 53개의 금화가 든 가방을 발견합니다. 당신은 모든 8개의 가방에 같은 수의 금화를 가지도록 금화를 재분배하기로 결정합니다. 모든 금화를 성공적으로 재분배했으며, 200개 이상의 금화를 가지고 있다는 것도 알게 됩니다. 53개의 금화가 든 가방을 발견하기 전, 당신이 가질 수 있었던 금화의 최소 개수는 얼마입니까?

풀이) 원래 7개의 가방 각각에 금화가 b개 있었다면, 7b + 53은 8로 나누어 떨어져야 합니다. 즉, 7b + 53 ≡ 0 (mod 8)입니다. 53 ≡ 5 (mod 8)이고 7 ≡ -1 (mod 8)이므로, -b ≡ -5 (mod 8)입니다. 양변에 -1을 곱하면, b ≡ 5 (mod 8)입니다. 이제 7b + 53 > 200이 되어야 하므로, b > (200 - 53) / 7 즉, b > 21입니다. 따라서 8로 나누었을 때 나머지가 5가 되는 21보다 큰 최소 정수는 29입니다. 그러므로 53개의 금화가 든 가방을 발견하기 전에는 29 × 7 = 203개의 금화를 가지고 있었습니다.

답) 203

문제) 다항식 x⁶ - 3을 x + 1로 나눌 때의 몫을 구하세요.

풀이) 우리는 나눗셈을 수행할 수 있습니다. 또는 나머지 정리에 의해, 나머지는 (-1)⁶ - 3 = -2입니다. 따라서, 우리는 다음과 같이 쓸 수 있습니다. (x⁶ - 3) / (x + 1) = ((x⁶ - 1) - 2) / (x + 1) = (x⁶ - 1) / (x + 1) - 2 / (x + 1) = ((x³ - 1)(x³ + 1)) / (x + 1) - 2 / (x + 1) = ((x³ - 1)(x + 1)(x² - x + 1)) / (x + 1) - 2 / (x + 1) = (x³ - 1)(x² - x + 1) - 2 / (x + 1) = x⁵ - x⁴ + x³ - x² + x - 1 - 2 / (x + 1). 따라서, 몫은 x⁵ - x⁴ + x³ - x² + x - 1입니다.

답) x⁵ - x⁴ + x³ - x² + x - 1

문제) 다음을 간단히 하세요: √(2.5² - 0.7²) / (2.7 - 2.5).

풀이) 다음과 같이 계산합니다: √(2.5² - 0.7²) / (2.7 - 2.5) = √(6.25 - 0.49) / 0.2 = √(5.76) / 0.2 = √(576/100) / 0.2 = √(576) / √(100) / 0.2 = 24 / 10 / 0.2 = 2.4 / 0.2 = 12.

답) 12

문제) 다음을 계산하세요: arcsin(-1/2). 답을 라디안으로 표현하세요.

풀이) sin(-π / 6) = -1/2 이므로, arcsin(-1/2) = -π / 6 입니다.

답) -π / 6

문제) 분수 3/20을 소수로 나타내세요.

풀이) 분자와 분모에 5를 곱하면 3/20 = 15/100 = 0.15입니다.

답) 0.15

문제) f가 다항식이고 (x-1) · f(x) = 3x⁴ + x³ - 25x² +38x -17 을 만족한다고 하자. f의 차수는 얼마인가?

풀이) 차수가 1인 다항식 (x-1)과 f의 곱이 차수가 4인 다항식이므로, f의 차수는 4-1 = 3 이다.

답) 3

문제) 첫 번째부터 N번째까지의 양의 홀수의 합이 121입니다. N의 값은 얼마입니까?

풀이) 첫 번째부터 N번째까지의 양의 홀수는 1, 3, ..., 2N - 1입니다. 등차수열의 합은 첫 번째 항과 마지막 항의 평균에 항의 개수를 곱한 것과 같습니다. 따라서 첫 번째부터 N번째까지의 양의 홀수의 합은 (1 + (2N - 1)) / 2 · N = N²입니다. N² = 121이라면, N = 11입니다.

답) 11

문제) Riproarin' Ringo는 반항적인 송아지를 밧줄로 잡고 있었습니다. Ringo는 송아지를 쫓아가기 전에 (1-i)⁸의 절대값을 계산하여 잠시 휴식을 주기로 했습니다. Ringo가 찾았어야 할 답은 무엇입니까?

풀이) 복소수의 크기는 곱셈적이라는 것을 알고 있습니다: |ab|의 크기는 |a| · |b|의 곱입니다. 따라서, |(1-i)⁸| = |1-i|⁸. 1-i의 크기는 √(1² + (-1)²) = √2입니다. 따라서 우리의 답은 (√2)⁸ = 16입니다. Ringo는 큰 휴식을 주지 않았습니다.

답) 16

문제) 머릿속으로 99² + 99 + 1을 계산하세요.

풀이) 첫 두 항을 인수분해하면 다음과 같습니다: 99² + 99 + 1 = 99(99 + 1) + 1 = 99 · 100 + 1 = 9900 + 1 = 9901.

답) 9901

문제) 50명의 학생이 있는 반에서, 28명은 MATHCOUNTS에 참여하고, 21명은 과학 동아리에 참여하며, 6명은 둘 다 참여하지 않습니다. MATHCOUNTS와 과학 동아리 둘 다 참여하는 학생은 몇 명입니까?

풀이) MATHCOUNTS 또는 과학 동아리에 참여하는 학생은 총 50 - 6 = 44명입니다. 이 중 MATHCOUNTS에 참여하지 않는 학생은 44 - 28 = 16명입니다. 이 16명은 모두 과학 동아리에만 참여합니다. 나머지 21 - 16 = 5명의 과학 동아리 참여자는 MATHCOUNTS에도 참여합니다.

답) 5

문제) 다항식 x³ - 3x² + 4x - 1은 x⁹ + px⁶ + qx³ + r의 인수입니다. 순서쌍 (p, q, r)을 입력하세요.

풀이) α를 x³ - 3x² + 4x - 1 = 0의 근이라고 하자. 그러면 α³ = 3α² - 4α + 1입니다. 따라서 α⁴ = 3α³ - 4α² + α = 3(3α² - 4α + 1) - 4α² + α = 5α² - 11α + 3입니다. 따라서, α⁶ = (3α² - 4α + 1)² = 9α⁴ - 24α³ + 22α² - 8α + 1 = 9(5α² - 11α + 3) - 24(3α² - 4α + 1) + 22α² - 8α + 1 = -5α² - 11α + 4, 그리고 α⁹ = α³ · α⁶ = (3α² - 4α + 1)(-5α² - 11α + 4) = -15α⁴ - 13α³ + 51α² - 27α + 4 = -15(5α² - 11α + 3) - 13(3α² - 4α + 1) + 51α² - 27α + 4 = -63α² + 190α - 54. 그러면 α⁹ + pα⁶ + qα³ + r = (-63α² + 190α - 54) + p(-5α² - 11α + 4) + q(3α² - 4α + 1) + r = (-5p + 3q - 63)α² + (-11p - 4q + 190)α + (4p + q + r - 54). 이를 0으로 만들기 위해 다음과 같이 설정합니다: -5p + 3q = 63, 11p + 4q = 190, 4p + q + r = 54. 이를 풀면 (p, q, r) = (6, 31, -1)입니다. 이러한 값들에 대해 α⁹ + pα⁶ + qα³ + r은 x³ - 3x² + 4x - 1의 모든 근에 대해 0이 되므로, x⁹ + px⁶ + qx³ + r은 x³ - 3x² + 4x - 1로 나누어집니다.

답) (6, 31, -1)

문제) 어떤 실수 a와 b에 대해, 다음 방정식 8x³ + 4ax² + 2bx + a = 0 은 서로 다른 세 개의 양의 근을 가집니다. 근의 밑이 2인 로그의 합이 5일 때, a의 값은 얼마입니까?

풀이) 근을 r₁, r₂, r₃라고 합시다. 그러면 5 = log₂ r₁ + log₂ r₂ + log₂ r₃ = log₂ (r₁ r₂ r₃) 이므로, r₁ r₂ r₃ = 2⁵ = 32입니다. 또한, 8x³ + 4ax² + 2bx + a = 8(x - r₁)(x - r₂)(x - r₃) 이므로, a = -8r₁ r₂ r₃ = -256입니다.

답) -256

문제) 모든 2차원 벡터 v에 대해 다음을 만족하는 가장 작은 양의 실수 C를 찾으세요. || (2 3 0 -2) v || ≤ C ||v|| 여기서 2차원 벡터 a에 대해 ||a||는 a의 크기입니다.

풀이) v = (x y)라고 하자. 그러면 ||v|| = ||(x y)|| = √(x² + y²)이고, || (2 3 0 -2) v || = || (2 3 0 -2) (x y) || = || (2x + 3y -2y) || = √((2x + 3y)² + (-2y)²) = √(4x² + 12xy + 13y²) 따라서 주어진 부등식은 √(4x² + 12xy + 13y²) ≤ C √(x² + y²) 또는 √((4x² + 12xy + 13y²) / (x² + y²)) ≤ C 로 변환됩니다. 따라서 C는 왼쪽 표현식의 최대값으로 생각할 수 있습니다. 왼쪽 표현식을 최대화하는 것은 그 제곱을 최대화하는 것과 같습니다. 즉, (4x² + 12xy + 13y²) / (x² + y²) 를 최대화하는 것입니다. 이 표현식의 가능한 값 k를 생각해보면, (4x² + 12xy + 13y²) / (x² + y²) = k 라는 방정식이 x와 y에 대해 해를 가집니다. 이 방정식을 다음과 같이 다시 쓸 수 있습니다. (4 - k)x² + 12xy + (13 - k)y² = 0 이 이차 표현식이 x와 y에 대해 해를 가지려면 판별식이 0 이상이어야 합니다. 즉, 12² - 4(4 - k)(13 - k) ≥ 0 또는 4k² - 68k + 64 ≤ 0입니다. 이 부등식은 4(k - 1)(k - 16) ≤ 0으로 인수분해됩니다. 이 부등식을 만족하는 k의 최대값은 16이므로, 우리가 찾는 C의 값은 √16 = 4입니다. 평등은 v = (1 2) 일 때 발생합니다.

답) 4

문제) 다항식 x⁸ + 3x⁴ - 4 = p₁(x) p₂(x) ⋯ pₖ(x) 에서, 각 비상수 다항식 pᵢ(x)는 계수가 정수인 모니크 다항식이며, 정수 범위에서 더 이상 인수분해할 수 없다고 하자. p₁(1) + p₂(1) + dots + pₖ(1)을 계산하시오.

풀이) 먼저, x⁸ + 3x⁴ - 4를 (x⁴ - 1)(x⁴ + 4)로 인수분해할 수 있습니다. 그러면 x⁴ - 1 = (x² + 1)(x² - 1) = (x² + 1)(x - 1)(x + 1) 이고, 소피 제르맹의 방법에 의해 x⁴ + 4 = x⁴ + 4x² + 4 - 4x² = (x² + 2)² - (2x)² = (x² + 2x + 2)(x² - 2x + 2) 입니다. 따라서 전체 인수분해는 x⁸ + 3x⁴ - 4 = (x² + 1)(x - 1)(x + 1)(x² + 2x + 2)(x² - 2x + 2) 입니다. 각 인수를 x = 1에서 평가하면, 2 + 0 + 2 + 5 + 1 = 10입니다.

답) 10

문제) 상수 a, b, c, d가 존재하여 모든 각도 x에 대해 다음이 성립합니다. (sin x)⁷ = a sin 7x + b sin 5x + c sin 3x + d sin x d를 찾으세요.

풀이) 다음과 같이 주어집니다. sin x = (exp(ix) - exp(-ix)) / 2i 따라서 이항 정리에 의해, sin⁷ x = ((exp(ix) - exp(-ix)) / 2i)⁷ = (1 / 128i⁷) (exp(7ix) - 7 exp(5ix) + 21 exp(3ix) - 35 exp(ix) + 35 exp(-ix) - 21 exp(-3ix) + 7exp(-5ix) - exp(-7ix)) = (i / 128) [(exp(7ix) - exp(-7ix)) - 7(exp(5ix) - exp(-5ix)) + 21(exp(3ix) - exp(-3ix)) - 35(exp(ix) - exp(-ix))] = (i / 128) (2i sin 7x - 14i sin 5x + 42i sin 3x - 70i sin x) = -1 / 64 sin 7x + 7 / 64 sin 5x - 21 / 64 sin 3x + 35 / 64 sin x. 따라서 우리가 찾는 상수 d는 35 / 64입니다.

답) 35 / 64

문제) 1^(2235423523)는 무엇입니까?

풀이) 1의 어떤 거듭제곱도 1이므로, 답은 1입니다.

답) 1

문제) 다음을 전개하고 완전히 단순화하세요: x(x(1+x)+2x)-3(x²-x+2)

풀이) 가장 안쪽 괄호부터 분배법칙을 적용합니다: x(x(1+x)+2x)-3(x²-x+2) = x(x+x²+2x) - 3(x²-x+2) 이제 다시 분배합니다: x²+x³+2x²-3x²+3x-6 마지막으로, 같은 항을 결합하여 다음을 얻습니다: x³+3x-6

답) x³+3x-6

문제) 정사각형의 두 개의 반대쪽 변의 길이가 40% 감소하고, 다른 두 변의 길이는 50% 증가하여 직사각형이 됩니다. 정사각형의 면적은 몇 퍼센트 감소합니까?

풀이) 정사각형의 면적을 A라고 합시다. 한 쌍의 반대쪽 변의 길이가 40% 감소했으므로 면적은 0.6A가 됩니다. 다른 쌍의 변은 50% 증가했으므로 면적은 1.5 · 0.6A = 0.9A가 됩니다. 따라서 면적은 10% 감소했습니다.

답) 10

문제) 어떤 x 값에 대해, 0 < x < 180, tan 53° tan 81° tan x° = tan 53° + tan 81° + tan x°. x를 구하시오.

풀이) tan x°를 고립시키면, tan x = (tan 53° + tan 81°) / (tan 53° tan 81° - 1) = -(tan 53° + tan 81°) / (1 - tan 53° tan 81°). 각 덧셈 공식에 따르면, 이는 -tan (53° + 81°) = -tan 134° = tan 46°와 같습니다. 따라서, x = 46입니다.

답) 46

문제) 복소수 z가 z⁵ = 1이고 z ≠ 1일 때, 다음을 계산하세요: z + 1/z + z² + 1/z².

풀이) 복소수 z가 z⁵ = 1이므로, z⁵ - 1 = 0입니다. 이는 다음과 같이 인수분해됩니다: (z - 1)(z⁴ + z³ + z² + z + 1) = 0. 여기서 z ≠ 1이므로, z⁴ + z³ + z² + z + 1 = 0입니다. 따라서, z + 1/z + z² + 1/z² = (z³ + z + z⁴ + 1) / z² = -z² / z² = -1.

답) -1

문제) 58₉ - 18₉을 계산하시오. 답은 9진법으로 나타내시오.

풀이) 이 뺄셈은 비교적 간단하다. 각 자리의 숫자를 그대로 빼면 된다. 받아내림은 필요 없다:

따라서, 정답은 40₉ 이다.

답) 40₉

문제) 이진수 10101001110₂는 8진수로 무엇입니까?

풀이) 2³ = 8이므로, 2진수와 8진수 표현 사이를 변환할 때 2진수의 각 3자리 블록을 8진수의 해당 값으로 대체할 수 있습니다. 이 경우, 마지막 세 자리는 110₂ = 6₈입니다. 다음 세 자리 블록은 001₂ = 1₈입니다. 계속해서, 다음 두 자리는 (오른쪽에서 왼쪽으로 이동하며) 101₂ = 5₈이고 010₂ = 2₈입니다. 모두 합치면, 10101001110₂ = 2516₈입니다.

답) 2516₈

문제) 부피와 표면적이 각각 입방 단위와 제곱 단위로 수치적으로 같은 구의 반지름의 길이는 몇 단위입니까?

풀이) 구의 부피는 (4/3)πr³이고, 표면적은 4πr²이므로, (4/3)πr³ = 4πr²입니다. 양변을 4πr²로 나누면, (1/3)r = 1이 됩니다. 따라서, r = 3입니다.

답) 3

문제) 연산 &는 양의 정수 a와 b에 대해 a & b = √(ab + a) / √(ab - b)로 정의됩니다. 9 & 2의 값을 구하세요. 답을 가장 간단한 형태의 분수로 표현하세요.

풀이) 9 & 2 = √((9)(2) + 9) / √((9)(2) - 2) = √(27) / √(16) = 3√(3) / 4 입니다.

답) 3√(3) / 4

문제) 다음을 간단히 하세요. sec x / sin x - sin x / cos x

풀이) 다음을 계산할 수 있습니다. sec x / sin x - sin x / cos x = 1 / (cos x · sin x) - sin x / cos x = (1 - sin² x) / (cos x · sin x) = cos² x / (cos x · sin x) = cos x / sin x = cot x

답) cot x

문제) 두 개의 공정한 6면체 주사위를 던집니다. 두 숫자의 곱이 5의 배수일 확률은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) 확률 문제는 때때로 사건이 발생하지 않을 경우의 수를 계산한 후 이를 빼서 답을 구할 수 있습니다. 이 문제에서 1, 2, 3, 4, 6의 면은 5 × 5 = 25개의 숫자 쌍을 만들어 그 곱이 5의 배수가 아닙니다. 따라서 36 - 25 = 11가지 방법으로 5의 배수를 얻을 수 있으며, 확률은 11 / 36입니다.

답) 11 / 36

문제) 함수 log x²의 정의역이 x < 0 또는 x > b일 때, a + b를 구하세요.

풀이) log x²가 정의되기 위해서는 x² > 0이어야 합니다. 이는 x = 0을 제외한 모든 x에 대해 참입니다. 따라서 이 함수의 정의역은 x 0입니다. 그러므로 답은 0 + 0 = 0입니다.

답) 0

문제) 만약 2⁸ = 4ˣ라면, x의 값은 무엇입니까?

풀이) 4를 2²로 다시 써서 4ˣ = 2²ˣ로 만듭니다. 2⁸ = 2²ˣ이므로, 2x = 8이 되어 x = 4임을 알 수 있습니다.

답) 4

문제) 함수 f(x) = x³ + 3x² + 1이 주어져 있습니다. 0이 아닌 실수 a와 b가 존재하여, f(x) - f(a) = (x - a)² (x - b)입니다. 순서쌍 (a,b)를 구하세요.

풀이) 나머지 정리에 의해, f(x) - f(a)는 x - a로 나누어 떨어지므로, x - a를 인수로 뺄 수 있습니다: f(x) - f(a) = (x³ + 3x² + 1) - (a³ + 3a² + 1) = (x³ - a³) + 3(x² - a²) = (x - a)(x² + ax + a²) + 3(x - a)(x + a) = (x - a)(x² + ax + a² + 3x + 3a) = (x - a)(x² + (a + 3)x + a² + 3a). 따라서, 우리는 다음과 같은 식을 원합니다: x² + (a + 3)x + a² + 3a = (x - a)(x - b) = x² - (a + b)x + ab. 계수를 비교하면, a + 3 = -a - b, a² + 3a = ab. a ≠ 0이므로, 두 번째 식의 양변을 a로 나누면 a + 3 = b가 됩니다. 그러면 -a - b = b이므로 a = -2b가 됩니다. 따라서 -2b + 3 = 2b - b, 이 식을 풀면 b = 1이 됩니다. 그러면 a = -2이므로, (a,b) = (-2,1)입니다.

답) (-2,1)

문제) 어떤 값의 x에 대해 2³·3ˣ = 72이 되는가?

풀이) 72의 소인수 분해는 72 = 2³·3²이므로, x = 2입니다.

답) 2

문제) 닫힌 구간 [-500, 500]에서 방정식 log(kx) = 2log(x+2)가 정확히 하나의 실수 해를 가지는 정수 k의 개수를 구하세요.

풀이) 먼저, k 0인 경우를 고려합니다. 이 경우, 지수 형태로 변환하면 kx = (x+2)² 또는 x² + (4-k)x + 4 = 0이 됩니다. 이 방정식의 해는 k > 0이므로 로그가 정의되는 x > 0에서 log(kx) = 2log(x+2)를 만족합니다. 따라서 이 이차 방정식은 정확히 하나의 양의 해를 가져야 합니다. 비에타의 정리에 따르면, 이 이차 방정식의 해의 곱은 4로 양수입니다. 따라서 정확히 하나의 양의 해를 가지려면 √4 = 2를 중근으로 가져야 합니다. 즉, x² + (4-k)x + 4 = (x-2)² = x² - 4x + 4가 되어야 하므로, 4-k = -4이고, k = 8입니다. 이는 조건을 만족하는 유일한 양의 k 값입니다. 총 500 + 1 = 501개의 k 값이 조건을 만족합니다.

답) 501

문제) 열 개의 트릭은 세 개의 스퀴그와 한 개의 굴리의 무게와 같습니다. 두 개의 트릭과 한 개의 굴리는 한 개의 스퀴그와 같은 무게입니다. 한 스퀴그의 무게는 몇 개의 트릭과 같습니까?

풀이) 트릭의 무게를 t, 스퀴그의 무게를 s, 굴리의 무게를 g라고 합시다. 주어진 정보에 따르면 다음과 같습니다. 10t = 3s + g 2t + g = s 우리는 s를 t에 대한 식으로 풀고자 하므로, g를 제거하고 싶습니다. 두 식을 더하면 다음과 같습니다. 10t + 2t + g = 3s + g + s 즉, 10t + 2t = 3s + s 따라서 4s = 12t 결국 s = 3t 따라서 한 스퀴그는 3개의 트릭과 같은 무게입니다.

답) 3

문제) 점 A는 대각선이 (0,0)과 (2,2)에 있는 정사각형의 내부 또는 경계에 위치합니다. 점 B는 대각선이 (4,2)와 (5,3)에 있는 정사각형의 내부 또는 경계에 위치합니다. 점 A와 B를 포함하는 직선의 기울기의 최댓값은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) 점 A는 축에 평행한 직사각형 영역에 제한되어 있으므로, A의 x와 y 좌표는 서로 독립적으로 선택할 수 있습니다. 점 B도 마찬가지입니다. 따라서 A와 B 사이의 수평 거리를 최소화하고 수직 거리를 최대화해야 합니다. B의 가능한 최대 y 좌표는 3이고, A의 가능한 최소 y 좌표는 0입니다. A의 가능한 최대 x 좌표는 2이고, B의 가능한 최소 x 좌표는 4입니다. 따라서 A와 B 사이의 기울기는 A가 (2,0)이고 B가 (4,3)일 때 최대화됩니다. 최대 기울기는 3 / 2입니다.

답) 3 / 2

문제) 다음을 만족하는 x를 구하세요: 3²ˣ + 19 = 10ˣ.

풀이) 3²ˣ를 (3²)ˣ = 9ˣ로 다시 쓰고, 양변에서 9ˣ를 빼면 19 = 10ˣ - 9ˣ가 됩니다. x ≤ 0일 때는 10ˣ나 9ˣ 모두 1보다 크지 않으므로 이 방정식의 해가 없습니다. x = 1, x = 2, x = 3을 시도해보면, x > 0일 때 10ˣ - 9ˣ는 증가하며, x = 2일 때 19가 됩니다. 참고: 미적분을 사용하여 x > 0일 때 10ˣ - 9ˣ가 단조 증가함을 증명할 수 있으며, 이는 우리가 찾은 해가 유일함을 증명합니다.

답) 2

문제) 다항식 3t²+5t+a와 4t²+bt-2의 곱이 12t⁴ + 26t³ - 8t² - 16t + 6입니다. a+b는 얼마입니까?

풀이) 두 다항식의 곱의 상수항은 두 상수항의 곱입니다. 따라서 6 = -2a이므로 a = -3입니다. 이제 다항식 곱의 일차항을 고려합니다. 이는 -16t = (5t·-2) + a·bt에서 주어집니다. 따라서 -16t = -10t + (-3)bt가 되고, b = 2입니다. 따라서 답은 a+b = -1입니다.

답) -1

문제) 원형 바닥을 가진 직립 원통형 탱크에 물이 시간당 20π 세제곱미터의 속도로 채워지고 있습니다. 탱크가 채워지면서 물의 높이는 시간당 4미터씩 상승합니다. 탱크의 반지름을 미터 단위로 구하세요. 답은 가장 간단한 근호 형태로 표현하세요.

풀이) 물의 부피는 매 시간 20π 세제곱미터씩 증가하고, 탱크 내 물의 높이는 매 시간 4미터씩 상승합니다. 직립 원통의 부피는 πr²h입니다. 1시간 동안의 부피와 높이의 변화를 고려하여 반지름을 구할 수 있습니다. πr²h_f - πr²h_0 = V_f - V_0 ⇒ πr²(Δh) = ΔV ⇒ πr²(4) = 20π ⇒ 4r² = 20 ⇒ r² = 5 반지름은 양수여야 하므로, r = √5 미터입니다.

답) √5

문제) 당신은 5개의 셔츠, 6개의 바지, 8개의 모자를 가지고 있습니다. 하나의 셔츠, 하나의 바지, 하나의 모자로 구성된 몇 가지의 옷차림을 만들 수 있습니까?

풀이) 셔츠는 5가지 선택이 가능하고, 바지는 6가지 선택이 가능하며, 모자는 8가지 선택이 가능합니다. 따라서 총 옷차림의 수는 5 × 6 × 8 = 240가지입니다.

답) 240

문제) 다음 방정식을 만족하는 가장 큰 값의 x를 찾으세요: |5x-1|=x+3.

풀이) 표현식 |5x-1|=x+3을 두 가지 경우로 나눌 수 있습니다. 첫 번째 경우는 다음과 같습니다. 5x-1 = x+3 ⇒ 4x = 4 ⇒ x = 1 이 값을 원래 방정식에 대입하여 확인하면, |5(1)-1|=1+3 또는 4=4가 됩니다. 이는 참이므로, x=1을 유효한 해로 받아들일 수 있습니다. 두 번째 경우는 다음과 같습니다. 5x-1 = -(x+3) 5x-1 = -x-3 ⇒ 6x = -2 ⇒ x = -1/3 이 값을 원래 방정식에 대입하면, |5(-1/3)-1| = -1/3+3이 되고, 이는 |-8/3| = 8/3 또는 8/3 = 8/3으로 단순화됩니다. 이것도 참이므로, x=-1/3을 유효한 해로 받아들일 수 있습니다. x=1과 x=-1/3 모두 가능한 값이므로, 최종 답은 두 값 중 더 큰 값인 x=1입니다.

답) 1

문제) 함수 f(x) 를 다음과 같이 정의합니다: f(x) = ax² (if x ≥ a), ax + 2a (if x < a). 여기서 a 는 어떤 수입니다. 함수 y = f(x) 의 그래프가 모든 수평선을 적어도 한 번 교차하도록 하는 a 의 최대값은 얼마입니까?

풀이) x 0입니다. a > 0일 때, 그래프의 직선 부분은 높이가 a² + 2a 이하인 모든 수평선을 지나고, 포물선 부분은 높이가 a³ 이상인 모든 수평선을 지납니다. 따라서 모든 수평선이 커버되기 위한 조건은 다음과 같습니다: a² + 2a ≥ a³. a > 0이므로, a로 나누면 a + 2 ≥ a². 따라서 0 ≥ a² - a - 2 = (a - 2)(a + 1). 이는 -1 ≤ a ≤ 2를 의미하며, a의 최대값은 2입니다. a = 2일 때 y = f(x)의 그래프는 아래와 같습니다 (비율은 맞지 않음). 포물선과 직선이 한 점에서 만나는 것을 확인할 수 있습니다. 아래는 도형을 그리는 코드입니다.

size(8cm);
import graph;

real a =2;
draw((-5,0)--(6,0),EndArrow());
draw((0,-6)--(0,14),EndArrow());

real g(real x) {return 0.5*a*(x-a)^2+a^3;}
real f(real x) {return a*x+2*a;}

draw(graph(f,-4.6,a),BeginArrow());
draw(graph(g,a,4.5),EndArrow());

label("$f(x)$",(0,15.5));
label("$x$",(6,0),E);
dot((2,8));

답) 2

문제) 3339, 2961, 1491의 최대 공약수를 구하세요.

풀이) 유클리드 알고리즘을 두 번 사용합니다. 먼저, 3339와 2961에 대해 사용합니다. gcd(3339, 2961) = gcd(3339 - 2961, 2961) = gcd(378, 2961) = gcd(378, 2961 - 378 · 7) = gcd(378, 315) = gcd(378 - 315, 315) = gcd(63, 315) 63은 315의 약수이므로, 3339와 2961의 최대 공약수는 63입니다. 다음으로, 63과 1491의 최대 공약수를 유클리드 알고리즘을 사용하여 찾습니다. gcd(63, 1491) = gcd(63, 1491 - 63 · 23) = gcd(63, 42) 63 = 3 · 21이고 42 = 2 · 21이므로, 최대 공약수는 21입니다.

답) 21

문제) Remmy는 10을 2/3으로 나누고 싶지만, 방법을 기억하지 못합니다. 그는 10에 어떤 숫자를 곱해야 답을 얻을 수 있을까요?

풀이) 분수로 나누는 것은 그 분수의 역수를 곱하는 것과 같습니다. 2/3의 역수는 3/2이므로, Remmy는 이것을 곱해야 합니다.

답) 3/2

문제) 함수 f(x) = √(x-1) / (x-2)가 실수 값을 가지려면, x의 가능한 최소 정수 값은 무엇입니까?

풀이) f(x)가 실수 값을 가지려면, 분자의 제곱근 안의 표현식이 0 이상이어야 하고 분모는 0이 아니어야 합니다. 따라서 두 가지 조건이 있습니다: x-1 ≥ 0, 즉 x ≥ 1, 그리고 x-2 ≠ 0, 즉 x ≠ 2. 이 두 조건을 모두 만족하는 가장 작은 정수 값은 x = 1입니다.

답) 1

문제) 해적이 묻힌 보물을 찾기 위해 7개의 섬을 탐색합니다. 각 섬에 보물이 있을 확률이 1/5일 때, 정확히 4개의 섬에 보물이 있을 확률은 얼마입니까?

풀이) 4개의 섬을 선택하는 방법은 35가지입니다 (7개 중 4개를 선택하는 조합). 각 선택에 대해, 그 4개의 섬에 보물이 있고 나머지 섬에는 보물이 없을 확률은 (1/5)⁴ · (4/5)³입니다. 따라서, 정확히 4개의 섬에 보물이 있을 확률은 35 · (1/5)⁴ · (4/5)³ = 448/15625입니다.

답) 448 / 15625

문제) 다음 방정식을 가진 원의 반지름이 1이 되도록 하는 c의 값은 얼마입니까? x² - 10x + y² + 6y + c = 0

풀이) 완전 제곱식을 만들면 (x - 5)² + (y + 3)² = 34 - c가 됩니다. 반지름이 1이 되려면 34 - c = 1²이어야 합니다. 따라서 c = 33입니다.

답) 33

문제) 사각형 ABCD에서 각 BAD와 각 CDA가 그림과 같이 삼등분됩니다. 각 AFD의 각도는 몇 도입니까? 아래는 도형을 그리는 코드입니다.

size(150);
pair A , B, C, D; A = (0,0); B = (2, 4); C = (7,4); D = (7, -2);
draw( (0,0)--(2,4) -- (7,4) -- (7, -2)-- cycle);
label("$A$", A, SW);
label("$B$", B, NW);
label("$C$", C, NE);
label("$D$", D, SE);
pair E, F;
E = (4.5-.2,1-.2); F = (5, 3);
draw(A--E--D); draw(A--F--D);
label("$E$", E, N); label("$F$", F, NW);
dot(A);dot(B);dot(C);dot(D);dot(E);dot(F);
label("$x$", (1, 1.5), S); label("$x$", (2, 1), S+W); label("$x$", (2, -1), N+N+N+W);
label("$y$", (5.5+.3, .5-.3), S); label("$y$", (6.5+.3, 0)); label("$y$", (5+.5, -1.5+.3));
label("$110^{\circ}$",(2.5,3.5)); label("$100^{\circ}$",(6.5-.2,3.5));

풀이) 삼각형 AFD의 총 각도는 180도여야 합니다. 다른 두 각의 크기가 2x와 2y이므로, 각 AFD는 180 - 2x - 2y = 180 - (2x + 2y) 도가 되어야 합니다. 이제 사각형 ABCD를 살펴보면, 내부 각의 합은 360도여야 합니다. 따라서 110도 + 100도 + 3y + 3x = 360도가 되어야 하므로, 3x + 3y = 150도가 됩니다. 우리는 2x + 2y를 찾고자 하므로, 양변에 2/3을 곱하여 2x + 2y = 100도가 됩니다. 이제 2x + 2y에 100도를 대입하여 각 AFD의 크기가 180 - (2x + 2y) = 180 - 100 = 80도임을 알 수 있습니다.

답) 80

문제) 벡터 (2, y, -5)를 벡터 (1, -2, 1)에 사영한 결과는 (5 / 6) (1, -2, 1) 입니다. y를 구하세요.

풀이) 벡터 (2, y, -5)를 벡터 (1, -2, 1)에 사영한 결과는 [(2, y, -5) · (1, -2, 1)] / [(1, -2, 1) · (1, -2, 1)] (1, -2, 1) = ((-2y - 3) / 6) (1, -2, 1). 따라서 -2y - 3 = 5이고, y = -4입니다.

답) -4

문제) 다음 방정식의 실근을 구하세요: (x + 1)(x - 3) / 5(x + 2)(x - 4) + (x + 3)(x - 5) / 9(x + 4)(x - 6) - 2(x + 5)(x - 7) / 13(x + 6)(x - 8) = 92 / 585. 실근을 쉼표로 구분하여 입력하세요.

풀이) 각 분자와 분모를 전개하면 다음과 같습니다: (x² - 2x - 3) / 5(x² - 2x - 8) + (x² - 2x - 15) / 9(x² - 2x - 24) - 2(x² - 2x - 35) / 13(x² - 2x - 48) = 92 / 585. 이를 다음과 같이 쓸 수 있습니다: (x² - 2x - 8 + 5) / 5(x² - 2x - 8) + (x² - 2x - 24 + 9) / 9(x² - 2x - 24) - 2(x² - 2x - 48 + 13) / 13(x² - 2x - 48) = 92 / 585. 따라서, 1/5 + 1/(x² - 2x - 8) + 1/9 + 1/(x² - 2x - 24) - 2/13 - 2/(x² - 2x - 48) = 92 / 585. 이것은 다음과 같이 단순화됩니다: 1/(x² - 2x - 8) + 1/(x² - 2x - 24) - 2/(x² - 2x - 48) = 0. y = x² - 2x - 48이라고 하면, 1/(y + 40) + 1/(y + 24) - 2/y = 0. 모든 항에 y(y + 24)(y + 40)을 곱하면, y(y + 24) + y(y + 40) - 2(y + 24)(y + 40) = 0. 이것은 64y + 1920 = 0으로 단순화되며, 따라서 y = -30입니다. 그러면 x² - 2x - 48 = -30이 되고, x² - 2x - 18 = 0이 됩니다. 이차 방정식의 해는 x = 1 ± √19입니다. (이 값들에 대해 분모가 0이 되지 않으므로, 이 값들은 허수해가 아닙니다.)

답) 1 ± √19

문제) 피겨 스케이터가 북쪽을 향해 서 있다가 오른쪽으로 회전을 시작합니다. 그녀는 2250도 회전합니다. 회전을 마쳤을 때 그녀는 어느 방향(북, 남, 동, 서)을 향하고 있습니까?

풀이) 각각의 완전한 회전은 360도입니다. 360을 2250으로 나누면 몫이 6이고 나머지가 90입니다. 따라서 그녀는 북쪽에서 오른쪽으로 90도 더 회전하여 동쪽을 향하게 됩니다.

답) 동쪽

문제) 다음을 단순화하세요: (-k + 4) + (-2 + 3k).

풀이) (-k + 4) + (-2 + 3k)를 계산하면, -k + 4 - 2 + 3k = 2k + 2입니다.

답) 2k + 2

100

문제) 벡터 a = (1, 1, 1) 일 때, a · v = 2 이고 a × v = (1, -2, 1) 인 벡터 v 를 찾으시오.

풀이) 벡터 v = (x, y, z) 라고 하자. 그러면 방정식 a · v = 2 에서 x + y + z = 2 이다. 또한, a × v = (1, 1, 1) × (x, y, z) = (-y + z, x - z, -x + y) 이다. 따라서, -y + z = 1, x - z = -2, -x + y = 1. 이 시스템과 x + y + z = 2 를 함께 풀면, x = -1/3, y = 2/3, z = 5/3 을 얻는다. 따라서, v = (-1/3, 2/3, 5/3) 이다.

답) (-1/3, 2/3, 5/3)

101

문제) 육각형이 원에 내접해 있습니다: 아래는 도형을 그리는 코드입니다.

pair pA, pB, pC, pD, pE, pF, pO;
pO = (0, 0);
pA = pO + dir(-10);
pB = pO + dir(60);
pC = pO + dir(130);
pD = pO + dir(170);
pE = pO + dir(-160);
pF = pO + dir(-80);
draw(pA--pB--pC--pD--pE--pF--pA);
label("$105^\circ$", pF, N * 2);
label("$110^\circ$", pB, SW * 1.5);
label("$\alpha$", pD, E);
draw(circle(pO, 1));

α의 크기는 몇 도입니까?

풀이) 꼭짓점을 라벨링하고 몇 개의 반지름을 그리면 큰 도움이 됩니다: 아래는 도형을 그리는 코드입니다.

pair pA, pB, pC, pD, pE, pF, pO;
pO = (0, 0);
pA = pO + dir(-10);
pB = pO + dir(60);
pC = pO + dir(130);
pD = pO + dir(170);
pE = pO + dir(-160);
pF = pO + dir(-80);
draw(pA--pB--pC--pD--pE--pF--pA);
draw(pA--pO--pC--pO--pE--pO, red);
draw(circle(pO, 1));
label("$O$", pO, NE);
label("$A$", pA, E);
label("$B$", pB, NE);
label("$C$", pC, NW);
label("$D$", pD, W);
label("$E$", pE, SW);
label("$F$", pF, S);
label("$105^\circ$", pF, N * 2);
label("$110^\circ$", pB, SW * 1.5);
label("$\alpha$", pD, E);

먼저, ∠ABC = 110°는 큰 호 AEC의 절반이어야 하므로, 호 AEC = 2 × ∠ABC입니다. 그러면 작은 호 AC는 360° - 2 × ∠ABC = 360° - 2 × 110° = 140°입니다. 마찬가지로, 작은 호 EA는 360° - 2 × ∠EFA = 360° - 2 × 105° = 150°이고, 작은 호 CE는 360° - 2α입니다. 이제 호 AC, CE, EA는 합쳐서 360°가 되어야 하므로, 360° = (360° - 2α) + 140° + 150° 360° = 650° - 2α 2α = 290° α = 145°입니다.

답) 145°

102

문제) 다음 방정식 x¹⁰ + (13x - 1)¹⁰ = 0 은 10개의 복소수 근 r₁, r̄₁, r₂, r̄₂, r₃, r̄₃, r₄, r̄₄, r₅, r̄₅를 가지며, 여기서 바는 복소수 켤레를 나타냅니다. 다음 값을 구하세요. 1 / (r₁ r̄₁) + 1 / (r₂ r̄₂) + 1 / (r₃ r̄₃) + 1 / (r₄ r̄₄) + 1 / (r₅ r̄₅)

풀이) p(x) = x¹⁰ + (13x - 1)¹⁰이라고 하자. 만약 r이 p(x)의 근이라면, r¹⁰ + (13r - 1)¹⁰ = 0입니다. 따라서 (13r - 1)¹⁰ = -r¹⁰이므로 -1 = ((13r - 1) / r)¹⁰ = (1 / r - 13)¹⁰입니다. 따라서 1 / r - 13의 크기는 1이므로 (1 / r - 13)(1 / r̄ - 13) = 1입니다. 따라서 (1 / r₁ - 13)(1 / r̄₁ - 13) + ... + (1 / r₅ - 13)(1 / r̄₅ - 13) = 5입니다. 전개하면, 1 / (r₁ r̄₁) + ... + 1 / (r₅ r̄₅) - 13(1 / r₁ + 1 / r̄₁ + ... + 1 / r₅ + 1 / r̄₅) + 5 · 169 = 5입니다. 1 / r₁, 1 / r̄₁, ..., 1 / r₅, 1 / r̄₅는 (1 / x)¹⁰ + (13 / x - 1)¹⁰ = 0의 해입니다. 즉, 1 + (13 - x)¹⁰ = 0입니다. 전개하면 x¹⁰ - 130x⁹ + ... = 0이므로, 비에타의 정리에 의해 1 / r₁ + 1 / r̄₁ + ... + 1 / r₅ + 1 / r̄₅ = 130입니다. 따라서, 1 / (r₁ r̄₁) + ... + 1 / (r₅ r̄₅) = 13 · 130 - 5 · 169 + 5 = 850입니다.

답) 850

103

문제) 식을 인수분해하세요: ab + 5b + 2a + 10.

풀이) 우리는 ab + 5b + 2a + 10 = ab + 5b + 2a + 2 · 5를 가지고 있습니다. 따라서 Simon의 즐겨 찾는 인수분해 트릭을 간단히 적용할 수 있습니다: ab + 5b + 2a + 10 = (a + 5)(b + 2).

답) (a + 5)(b + 2)

104

문제) 상수 λ 가 0 ≤ λ ≤ 4 일 때, 함수 f : [0,1] to [0,1] 가 다음과 같이 정의됩니다: f(x) = λx(1 - x). f(x) ≠ x 이지만 f(f(x)) = x 인 x in [0,1] 가 존재하는 λ 의 값을 찾으세요. 0 ≤ λ ≤ 4 .

풀이) 우리는 다음을 가집니다: f(f(x)) = f(λx(1 - x)) = λ · λx(1 - x)(1 - λx(1 - x)), 따라서 λ · λx(1 - x)(1 - λx(1 - x)) = x 를 풀고자 합니다. 만약 f(x) = x 라면, f(f(x)) = f(x) = x 이므로, λx(1 - x) = x 의 근은 λ · λx(1 - x)(1 - λx(1 - x)) = x 의 근이기도 합니다. 따라서 λx(1 - x) - x 는 λ · λx(1 - x)(1 - λx(1 - x)) - x 의 인수일 것입니다. 실제로, λ · λx(1 - x)(1 - λx(1 - x)) - x = (λx(1 - x) - x)(λ²x² - (λ² + λ)x + λ + 1). λ²x² - (λ² + λ)x + λ + 1 의 판별식은 (λ² + λ)² - 4λ²(λ + 1) = λ⁴ - 2λ³ - 3λ² = λ²(λ + 1)(λ - 3). 이는 λ = 0 또는 3 ≤ λ ≤ 4 일 때 비음이 아닙니다. 만약 λ = 0 이라면, 모든 x in [0,1] 에 대해 f(x) = 0 입니다. 만약 λ = 3 이라면, 방정식 f(f(x)) = x 는 (3x(1 - x) - x)(9x² - 12x + 4) = 0. 9x² - 12x + 4 = 0 의 근은 모두 2 / 3 이며, 이는 f(x) = x 를 만족합니다. 반면, λ > 3 일 때, λx(1 - x) = x 의 근은 x = 0 과 x = λ - 1 / λ 입니다. 분명히 x = 0 은 λ²x² - (λ² + λ)x + λ + 1 = 0 의 근이 아닙니다. 또한, 만약 x = λ - 1 / λ 이라면, λ²x² - (λ² + λ)x + λ + 1 = λ²(λ - 1 / λ)² - (λ² + λ) · λ - 1 / λ + λ + 1 = 3 - λ ≠ 0. 게다가, 근의 곱은 λ + 1 / λ² 로 양수이므로, 두 근 모두 양수이거나 음수입니다. 근의 합은 λ² + λ / λ² > 0 이므로 두 근 모두 양수입니다. 또한, λ² + λ / λ = 1 + 1 / λ < 4 / 3 이므로 적어도 하나의 근은 1보다 작아야 합니다. 따라서 주어진 조건을 만족하는 λ 의 집합은 λ in (3,4] 입니다.

답) (3,4]

105

문제) 다음 두 그래프 x² + y² + 6x - 24y + 72 = 0 와 x² - y² + 6x + 16y - 46 = 0 는 네 점에서 교차합니다. 이 네 점에서 점 (-3,2)까지의 거리의 합을 구하세요.

풀이) 두 방정식을 더하면, 2x² + 12x - 8y + 26 = 0 또는 x² + 6x - 4y + 13 = 0 입니다. 이 방정식을 (x + 3)² = 4(y - 1) 로 쓸 수 있습니다. 이는 초점이 (-3,2)이고 준선이 y = 0인 포물선의 방정식입니다. 아래는 도형을 그리는 코드입니다.

unitsize(1 cm);

real parab (real x) {
 return ((x^2 + 6*x + 13)/4);
}

pair P = (-0.5,parab(-0.5));

draw(graph(parab,-6,0));
draw((-3,2)--P--(-0.5,0));

dot((-3,2));
dot((-3,1));
draw((-6,0)--(0,0),dashed);

포물선의 정의에 따르면, 포물선 위의 임의의 점 P에서 초점까지의 거리는 P에서 y축까지의 거리와 같습니다. 이는 점의 y좌표입니다. 주어진 방정식을 빼면, 2y² - 40y + 118 = 0 또는 y² - 20y + 59 = 0 입니다. 이 이차방정식의 근을 y₁과 y₂라고 합시다. 그러면 교차점의 y좌표는 y₁ 또는 y₂이어야 합니다. 방정식 x² + y² + 6x - 24xy + 72 = 0은 원을 나타내므로, 직선 y = y₁과 최대 두 점에서 교차하고, 직선 y = y₂도 최대 두 점에서 교차합니다. 따라서 네 교차점의 y좌표는 y₁, y₁, y₂, y₂이며, 그 합은 2y₁ + 2y₂입니다. 비에타의 정리에 따르면, y₁ + y₂ = 20이므로, 2y₁ + 2y₂ = 40입니다.

답) 40

106

문제) 아래에 나열된 8개 카운티에 대해, 2005년 학생 수의 중앙값은 얼마입니까?

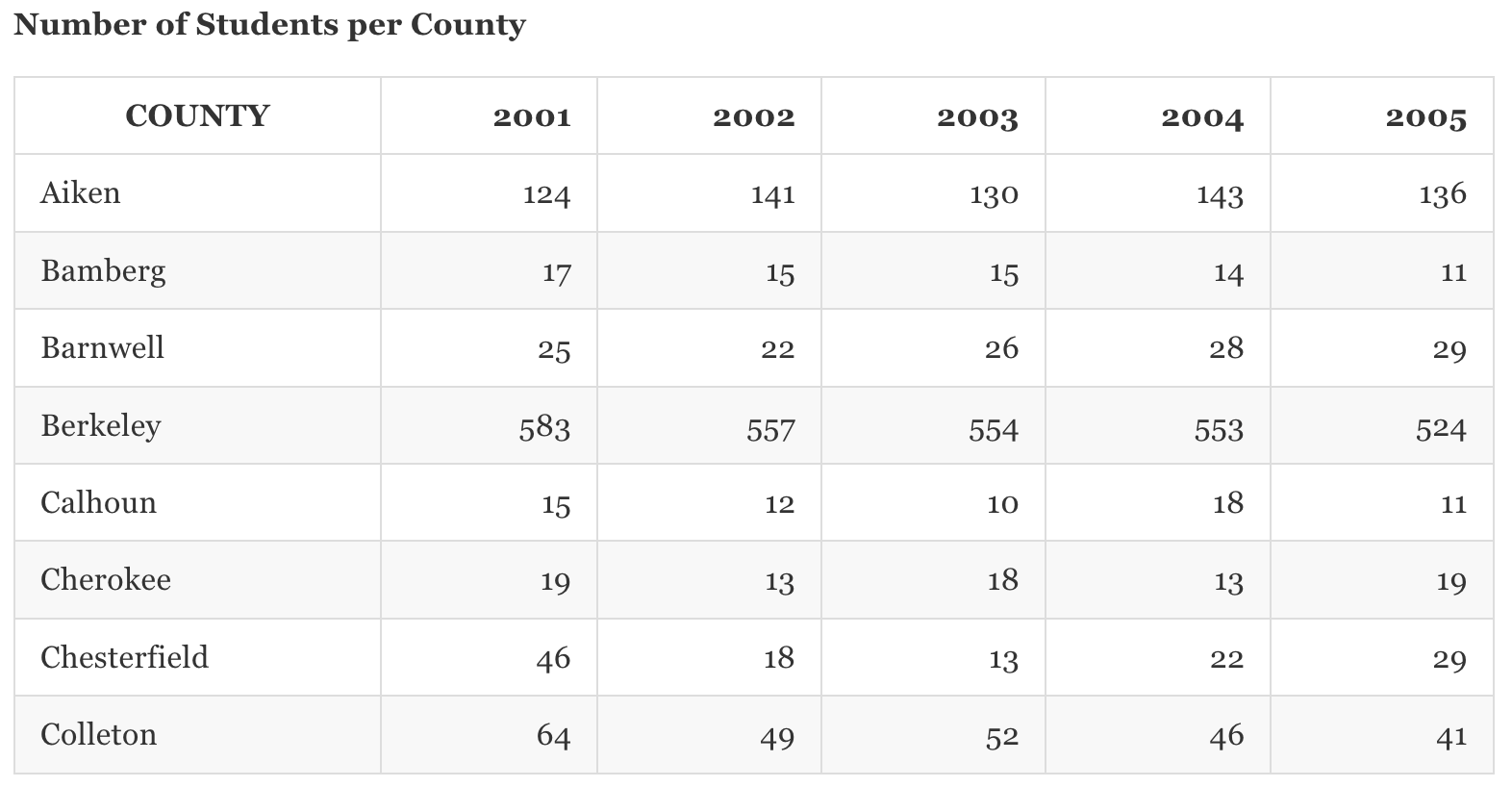
풀이) 값의 집합에서 중앙값은 집합의 절반 값보다 크고 나머지 절반 값보다 작은 수입니다. 값의 개수가 짝수인 경우, 중앙값은 두 "중간" 값의 평균입니다. 8개의 카운티가 있으므로, 학생 수의 중앙값은 학생 수가 4번째로 많은 카운티와 5번째로 많은 카운티의 학생 수의 평균입니다. 표를 보면, 이 두 카운티 모두 29명의 학생이 있으므로, 학생 수의 중앙값은 29명입니다.

답) 29

107

문제) 방정식 y = (4x³ + 2x - 4) / (3x³ - 2x² + 5x - 1)의 그래프에 대해 수평 점근선이 존재하는 y 값은 얼마입니까?

풀이) 유리 함수에서 분자와 분모의 차수가 같을 때, 수평 점근선은 분자의 최고차항의 계수를 분모의 최고차항의 계수로 나눈 값입니다. 이를 확인하기 위해, 분자와 분모를 x³로 나누어 다음과 같이 표현합니다. (4 + 2/x² - 4/x³) / (3 - 2/x + 5/x² - 1/x³) x가 ∞ 또는 -∞로 갈 때, x와 관련된 항들은 0에 가까워지므로 전체 식은 4/3에 가까워집니다. 따라서 수평 점근선은 하나만 존재하며, y = 4/3에 있습니다.

답) 4/3

108

문제) 30보다 작은 모든 소수의 집합과 0보다 큰 모든 홀수의 집합의 교집합에는 몇 개의 원소가 있습니까?

풀이) 다시 말해, 30보다 작은 양의 홀수 소수의 개수를 찾는 것입니다. 30보다 작은 모든 홀수를 살펴보고 그 중 몇 개가 소수인지 확인합니다. 3, 5, 7, 11, 13, 17, 19, 23, 29가 30보다 작은 양의 홀수 소수이며, 교집합에는 총 9개의 원소가 있습니다.

답) 9

109

문제) 타원 kx² + y² = 1의 두 초점을 F₁, F₂라 하자. 여기서 k > 1은 상수이다. F₁과 F₂를 지나고, x축 위의 두 점에서 타원에 접하는 원이 존재한다고 하자. k의 값을 구하여라.

풀이) 타원의 식을 x²/(1/√k)² + y²/1² = 1의 형태로 쓰면, 가로 반축(준단축)의 길이는 1/√k, 세로 반축(준장축)의 길이는 1임을 알 수 있다. k > 1이므로 세로축이 더 길어 장축이 된다. 따라서 중심(원점)에서 각 초점까지의 거리 c는 c = √(1 − (√(1/k))²) = √(1 − 1/k) = √(k−1)/√k 이다.

size(7cm);
draw((0,-1.4)--(0,1.4),EndArrow); label("$y$",(0,1.4),N);
draw((-1.2,0)--(1.2,0),EndArrow); label("$x$",(1.2,0),E);
draw(xscale(1/sqrt(2))*unitcircle);
draw(scale(1/sqrt(2),1/sqrt(2))*unitcircle);
dot("$F_1$",(0,1/sqrt(2)),NW);
dot("$F_2$",(0,-1/sqrt(2)),SW);

이와 같은 원이 존재한다는 것은, 원점이 각 초점 F₁, F₂와 가로축(준단축) 양 끝점까지의 거리가 같다는 뜻이다. 가로축의 끝점은 (±1/√k, 0)이므로 원점에서 그 점까지의 거리는 1/√k이다. 따라서 √(k−1)/√k = 1/√k 이고, 양변에 √k를 곱하면 √(k−1) = 1이 된다. 그러므로 k−1 = 1, 즉 k = 2이다.

답)

110

문제) 다음 식을 만족하는 가장 작은 양의 각 θ의 도 단위 값을 구하세요. tan θ = (cos 5° cos 20° + cos 35° cos 50° - sin 5° sin 20° - sin 35° sin 50°) / (sin 5° cos 20° - sin 35° cos 50° + cos 5° sin 20° - cos 35° sin 50°).

풀이) 각도 덧셈 공식에 따르면, 분자는 (cos 5° cos 20° - sin 5° sin 20°) + (cos 35° cos 50° - sin 35° sin 50°) = cos(5° + 20°) + cos(35° + 50°) = cos 25° + cos 85°입니다. 합차 공식에 따르면, cos 25° + cos 85° = 2 cos 55° cos 30°입니다. 유사하게, 분모는 (sin 5° cos 20° + cos 5° sin 20°) - (sin 35° cos 50° + cos 35° sin 50°) = sin(5° + 20°) - sin(35° + 50°) = sin 25° - sin 85° = -2 sin 30° cos 55°입니다. 따라서 식은 2 cos 55° cos 30° / -2 sin 30° cos 55° = -cos 30° / sin 30° = -√3 = tan 120°입니다. 따라서, 가장 작은 θ는 120°입니다.

답) 120°

111

문제) 양의 정수로 이루어진 엄격히 증가하는 수열 a₁, a₂, a₃, ... 에 대해 모든 양의 정수 k에 대해 부분 수열 a₂ₖ₋₁, a₂ₖ, a₂ₖ₊₁은 기하수열이고, 부분 수열 a₂ₖ, a₂ₖ₊₁, a₂ₖ₊₂는 등차수열입니다. a₁₃ = 2016일 때, a₁을 구하세요.

풀이) a₂ / a₁ = b / a 라고 하자. 여기서 a와 b는 서로소인 양의 정수이며, a a₄ = 2a₃ - a₂ = 2cb² - cab = cb(2b - a), a₅ = a₄² / a₃ = [cb(2b - a)]² / (cb²) = c(2b - a)², a₆ = 2a₅ - a₄ = 2c(2b - a)² - cb(2b - a) = c(2b - a)(3b - 2a), a₇ = a₆² / a₅ = [c(2b - a)(3b - 2a)]² / c(2b - a)² = c(3b - 2a)², a₈ = 2a₇ - a₆ = 2c(3b - 2a)² - c(2b - a)(3b - 2a) = c(3b - 2a)(4b - 3a), a₉ = a₈² / a₇ = [c(3b - 2a)(4b - 3a)]² / [c(3b - 2a)²] = c(4b - 3a)², 이와 같이 계속됩니다. 일반적으로, 귀납법을 통해 다음을 증명할 수 있습니다: a₂ₖ = c[(k - 1)b - (k - 2)a][kb - (k - 1)a], a₂ₖ₊₁ = c[kb - (k - 1)a]², 모든 양의 정수 k에 대해. 따라서, a₁₃ = 2016에서, c(6b - 5a)² = 2016 = 2⁵ · 3² · 7 = 14 · 12²입니다. 따라서, 6b - 5a는 12의 약수여야 합니다. n = 6b - 5a라고 하자. 그러면 a < a + 6(b - a) = n이고, n - a = 6b - 6a = 6(b - a)이므로, n - a는 6의 배수입니다. 따라서, 6 < a + 6 ≤ n ≤ 12이고, 유일한 해는 (a, b, n) = (6, 7, 12)입니다. 그러면 c = 14이고, a₁ = 14 · 6² = 504입니다.

답) 504

112

문제) Brennan 씨의 통계 수업에는 7명의 남학생과 4명의 여학생이 있습니다. 내일 그룹 발표를 위해 3명의 남학생과 2명의 여학생을 선택하는 방법은 몇 가지입니까? (남학생과 여학생을 선택하는 순서는 중요하지 않습니다.)

풀이) 첫 번째 여학생을 선택하는 방법은 4가지이고, 두 번째 여학생을 선택하는 방법은 3가지입니다. 그러나 여학생 A를 먼저 선택하고 여학생 B를 선택하는 경우와 여학생 B를 먼저 선택하고 여학생 A를 선택하는 경우가 동일하므로, 여학생을 선택하는 총 방법의 수는 4 × 3 / 2 = 6가지입니다. 마찬가지로, 첫 번째 남학생을 선택하는 방법은 7가지, 두 번째 남학생을 선택하는 방법은 6가지, 마지막 남학생을 선택하는 방법은 5가지입니다. 하지만 이 경우 각 남학생 조합이 6번씩 계산되므로, 남학생을 선택하는 총 방법의 수는 7 × 6 × 5 / (3 × 2) = 35가지입니다. 따라서 그룹 발표를 위해 학생들을 선택하는 총 방법의 수는 4 × 3 / 2 · 7 × 6 × 5 / (3 × 2) = 210가지입니다.

답) 210

113

문제) 다음을 간단히 하세요: (1 + √2) / (2 + √3). 당신의 해를 A(1 + √B) - (√C + √D) 형태로 변환할 수 있습니다. 여기서 A, B, C, D는 양의 정수입니다. A + B + C + D는 무엇입니까?

풀이) 분자와 분모에 켤레를 곱하면, (1 + √2) / (2 + √3) = ((1 + √2)(2 - √3)) / ((2 + √3)(2 - √3)) = (2 - √3 + 2√2 - √6) / (4 - 3) = 2 - √3 + 2√2 - √6이 됩니다. 따라서 A = 2, B = 2, C = 3, D = 6 (C와 D는 교환 가능)입니다. 그래서 A + B + C + D = 2 + 2 + 3 + 6 = 13입니다.

답) 13

114

문제) 다음 식의 값을 구하세요: (26² - 24² - 10)² - 10².

풀이) 우리는 x² - y² = (x+y)(x-y)라는 공식을 알고 있습니다. 먼저, x = 26² - 24² - 10 그리고 y = 10이라고 합시다. x² - y²를 인수분해하고 대입하면 (26² - 24² - 10 + 10)(26² - 24² - 10 - 10)이 됩니다. 이제, x = 26 그리고 y = 24라고 합시다. x² - y²를 인수분해하고 대입하면 ((26 + 24)(26 - 24) - 10 + 10)((26 + 24)(26 - 24) - 10 - 10)이 됩니다. 이는 (50 · 2)(50 · 2 - 20)로 간단해지며, 100 · 80이 됩니다. 따라서, 최종 답은 8000입니다.

답) 8000

115

문제) 정수 C와 D에 대해 다음 식이 모든 실수 x에 대해 성립할 때, C와 D의 곱 CD를 구하세요. 단, x ≠ -8, 3입니다. C/(x-3) + D/(x+8) = (4x-23)/(x²+5x-24)

풀이) 먼저, 우변의 분모를 인수분해하면 다음과 같습니다. C/(x - 3) + D/(x + 8) = (4x - 23)/((x - 3)(x + 8)) 양변에 (x - 3)(x + 8)을 곱하면, C(x + 8) + D(x - 3) = 4x - 23 적절한 x 값을 대입하여 C와 D를 구할 수 있습니다. 예를 들어, x = 3을 대입하면 11C = -11이므로 C = -1입니다. x = -8을 대입하면 -11D = -55이므로 D = 5입니다. (이는 적절하지 않아 보일 수 있지만, 주어진 식이 x ≠ -8, 3을 제외한 모든 x에 대해 성립한다고 했습니다. 이는 식 C(x + 8) + D(x - 3) = 4x - 23이 x의 무한한 값에 대해 성립한다는 것을 의미하며, 두 다항식이 무한한 값에 대해 같다면 모든 x에 대해 같다는 것을 의미합니다. 따라서 이 식에 임의의 값을 대입할 수 있습니다.) 따라서, CD = (-1) · 5 = -5입니다.

답) -5

116

문제) 단어 ELLIPSE의 문자를 배열하는 방법의 수를 구하세요.

풀이) E가 두 개, L이 두 개, 총 7개의 문자가 있으므로, 답은 7! / (2! × 2!) = 1260입니다.

답) 1260

117

문제) 다음을 풀어 x를 구하세요: 2²ˣ = √(256).

풀이) 2²ˣ = √(256) ⇔ 2²ˣ = (2⁸)^1/2 ⇔ 2²ˣ = 2⁴ ⇔ 2x = 4 ⇔ x = 2

답) 2

118

문제) 만약 √(3x - 5) = 2라면, 가능한 모든 x의 값을 찾으세요.

풀이) 먼저, 양변을 제곱합니다. (√(3x - 5))² = 2² 따라서, 3x - 5 = 4 3x = 9 x = 3 테스트해보면, 이 x 값이 원래 방정식을 만족함을 알 수 있습니다.

답) 3

119

문제) 정수 쌍 (a, b)의 개수를 구하세요. 여기서 |a + bi| ≤ 5입니다.

풀이) 문제는 원점에 중심을 두고 반지름이 5인 원 안에 있거나 위에 있는 정수 실수부와 허수부를 가진 복소수의 개수를 세는 것입니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.5 cm);

int i, j;

draw((-5,0)--(5,0));
draw((0,-5)--(0,5));
draw(Circle((0,0),5));

for (i = -5; i <= 5; ++i) {
for (j = -5; j <= 5; ++j) {
 if (i^2 + j^2 > 25) {dot((i,j));}
 if (i^2 + j^2 <= 25) {dot((i,j),red);}
}}

첫 번째 사분면에는 (축을 포함하지 않고) 15개의 복소수가 있습니다. 양의 실수 축, 음의 실수 축, 양의 허수 축, 음의 허수 축에는 각각 5개의 복소수가 있습니다. 마지막으로 원점 자체가 있으며, 이는 총 4 × 15 + 4 × 5 + 1 = 81개의 복소수를 제공합니다.

답) 81

120

문제) 식 1 + 2 + 3 - 4 + 5 + 6은 13과 같습니다. 다양한 위치에 괄호를 추가하면 이 값을 변경할 수 있습니다. 예를 들어, 1+2+3-(4+5)+6=1+2+3-9+6=6-9+6=3입니다. 괄호만 추가하고 항의 순서를 변경하지 않으면, 이 식이 가질 수 있는 최소값은 얼마입니까? (이 문제에서는 덧셈이나 뺄셈을 곱셈으로 변경할 수 없습니다. 예를 들어, (1+2+3)(-4)+5+6은 괄호의 유효한 배치가 아닙니다.) 답을 하나의 값으로 입력하세요.

풀이) 뺄셈 기호 이전의 모든 항은 더해지며, 덧셈은 결합법칙이 적용되므로 괄호를 추가해도 값이 변하지 않습니다. 그러나 뺄셈은 결합법칙이 적용되지 않습니다. 이 식의 값을 최소화하려면 가능한 한 많은 값을 빼야 합니다. 따라서 식은 다음과 같이 괄호를 배치할 때 최소화됩니다: 1+2+3-(4+5+6). 이는 1+2+3-15 = 6-15로 단순화되며, 결과는 -9입니다.

답) -9

121

문제) 함수 f(x)는 홀수 함수이고, 함수 g(x)는 짝수 함수입니다. f(f(g(f(g(f(x))))))는 짝수 함수, 홀수 함수, 아니면 둘 다 아닐까요? "odd", "even", "neither" 중 하나를 입력하세요.

풀이) 다음과 같이 계산할 수 있습니다: f(f(g(f(g(f(-x)))))) = f(f(g(f(g(-f(x)))))) = f(f(g(f(g(f(x)))))) 따라서 이 함수는 짝수 함수입니다. 일반적으로, 함수의 합성에서 적어도 하나의 함수가 짝수 함수라면, 전체 합성 함수는 짝수 함수가 됩니다.

답) 짝수

122

문제) 다음을 풀어 x를 구하세요: x / 2 + x / 3 = 5

풀이) 좌변을 공통 분모로 작성하면, x / 2 + x / 3 = 3x / 6 + 2x / 6 = 5x / 6 따라서 우리의 방정식은 5x / 6 = 5입니다. 양변에 6 / 5를 곱하면 x = 5 · (6 / 5) = 6입니다.

답) 6

123

문제) Daniel은 전자 제품 매장에서 일하며, 텔레비전의 인기도(판매 수량으로 측정됨)가 그 비용에 반비례한다고 주장합니다. 만약 15명의 고객이 1500짜리 텔레비전을 구매한다면, Daniel의 이론에 따르면 2500짜리 텔레비전을 몇 명의 고객이 구매할까요?

풀이) 텔레비전의 인기도(또는 구매하는 고객 수)를 p라고 하고, 텔레비전의 비용을 c라고 합시다. Daniel의 이론에 따르면, p와 c는 반비례합니다. 따라서 (p)(c) = k라는 일정한 값 k가 존재합니다. p = 15일 때 c = 1500이라면, k = (15)(1500) = 22500입니다. 그러므로 c = 2500일 때, (p)(c) = k ⇒ (p)(2500) = 22500 ⇒ p = 22500 / 2500 = 9. Daniel의 이론에 따르면, 9명의 고객이 2500짜리 텔레비전을 구매할 것입니다.

답) 9

124

문제) 도형에서, D와 E는 선분 AB와 선분 BC의 중점입니다. 사각형 DBEF의 넓이를 구하세요. 아래는 도형을 그리는 코드입니다.

size(180); defaultpen(linewidth(.7pt)+fontsize(10pt));
pair A, B, C, D, E, F;
A=(0,6);
B=(0,0);
C=(8,0);
D=(0,3);
E=(4,0);
F=(8/3,2);
draw(E--A--C--D);
draw((-1,0)--(10,0), EndArrow);
draw((0,-1)--(0,8), EndArrow);
label("$A(0,6)$", A, W);
label("$B(0,0)$", B, SW);
label("$C(8,0)$", C, S);
label("$D$", D, W);
label("$E$", E, S);
label("$F$", F, SW);
label("$x$", (10,0), dir(0));
label("$y$", (0,8), dir(90));

풀이) 삼각형 DBC는 밑변 BC의 길이가 8이고 높이 BD의 길이가 3이므로, 그 넓이는 1/2 × 8 × 3 = 12입니다. 사각형 DBEF의 넓이는 삼각형 DBC의 넓이에서 삼각형 FEC의 넓이를 뺀 값입니다. 삼각형 FEC는 밑변 EC = BC - BE = 8 - 4 = 4입니다. 삼각형 FEC의 높이는 점 F에서 x축까지의 수직 거리로, 이는 점 F의 y좌표인 2와 같습니다. 따라서 삼각형 FEC의 넓이는 1/2 × 4 × 2 = 4입니다. 결론적으로, 사각형 DBEF의 넓이는 12 - 4 = 8입니다.

답) 8

125

문제) 만약 |x+5|-|3x-6|=0이라면, x의 가능한 최대 값을 구하세요. 답을 대분수로 표현하세요.

풀이) 우선, 두 번째 부등식을 방정식의 오른쪽으로 이동하여 |x+5|=|3x-6|을 얻습니다. 여기서 방정식을 두 개의 경우로 나눌 수 있습니다. 첫 번째 경우, x+5와 3x-6이 같은 부호를 가지면, x+5=3x-6입니다. 경우 1: x+5=3x-6 ⇒ -2x=-11 ⇒ x=11/2 이 x 값을 원래 방정식에 대입하여 답을 확인하면, |11/2+5|-|3(11/2)-6|=0 또는 0=0이 됩니다. 이는 참이므로, x=11/2를 유효한 해로 받아들일 수 있습니다. 두 번째 경우, x+5와 3x-6이 다른 부호를 가지면, x+5=-(3x-6)입니다. 경우 2: x+5=-(3x-6) x+5=-3x+6 ⇒ 4x=1 ⇒ x=1/4 이 x 값을 원래 방정식에 대입하여 답을 확인하면, |1/4+5|-|3(1/4)-6|=0이 되어, 0=0이 됩니다. 이는 항상 참이므로, x=1/4를 유효한 해로 받아들일 수 있습니다. 따라서, 가능한 두 해는 1/4와 11/2입니다. 문제에서 x의 가능한 최대 값을 묻고 있으므로, 최종 해는 11/2입니다.

답) 11/2

126

문제) (3.6)²의 천장값을 구하고, 그 값에서 (3.6의 천장값)²를 뺀 값을 구하시오.

풀이) (3.6)²의 천장값은 ⌈12.96⌉ = 13입니다. 왜냐하면 12.96보다 큰 최소의 정수는 13이기 때문입니다. (⌈3.6⌉)²는 4² = 16입니다. 왜냐하면 3.6보다 큰 최소의 정수는 4이기 때문입니다. 따라서, 답은 13 - 16 = -3입니다.

답) -3

127

문제) 복소수 z ≠ i에 대해 F(z)=(z+i) / (z-i)로 정의된 함수가 있습니다. 모든 양의 정수 n에 대해 z_n = F(z_n-1)입니다. z₀=1 / 137+i일 때, z₂₀₀₂를 구하세요.

풀이) 함수 F를 몇 번 반복 적용해 봅시다. z_k+3 = z_k가 모든 k에 대해 성립합니다. 2002 ≡ 1 (mod 3)이므로, z₂₀₀₂ = z₁ = (z₀+i) / (z₀-i) = 1/137 + 2i / 1/137 = 1+274i.

답) 1+274i

128

문제) 10진수 555를 5진수로 표현하세요.

풀이) 555를 5의 거듭제곱으로 표현합니다. 555보다 작은 5의 가장 큰 거듭제곱은 5³ = 125이고, 555보다 작은 125의 최대 배수는 4입니다. 따라서 555 - 4 · 125 = 55입니다. 55보다 작은 5의 가장 큰 거듭제곱은 5²=25이고, 55보다 작은 25의 최대 배수는 2입니다. 따라서 55 - 2 · 25 = 5이며, 이는 5¹입니다. 따라서 555는 4 · 5³ + 2 · 5² + 1 · 5¹로 쓸 수 있습니다. 따라서, 답은 4210₅입니다.

답) 4210₅

129

문제) 수잔은 매 3일마다 4마일을 걷습니다. 그녀가 2월에 걸을 수 있는 최소 마일 수는 얼마입니까?

풀이) 2월은 28일이며, 윤년에는 하루가 더 있습니다. 최소 마일 수를 구하려면 2월을 28일로 가정합니다. 그녀가 걸을 수 있는 최소 일수는 ⌊28 / 3⌋ = 9일입니다. 따라서 그녀가 걸을 수 있는 최소 마일 수는 9 · 4 = 36 마일입니다.

답) 36

130

문제) 삼각형 ABC에서, AB = 17, AC = 8, BC = 15입니다. C에서 AB로 내린 높이의 발을 D라고 할 때, 삼각형 ACD의 넓이를 구하세요.

풀이) 피타고라스 정리에 의해, ∠C = 90°. 삼각형 ACD와 ABC는 닮음이므로, CD = BC · (AC / AB) = 15 · (8 / 17) = 120 / 17, 그리고 AD = AC · (AC / AB) = 8 · (8 / 17) = 64 / 17. 아래는 도형을 그리는 코드입니다.

unitsize(0.4 cm);

pair A, B, C, D;

A = (0,8);
B = (15,0);
C = (0,0);
D = (C + reflect(A,B)*(C))/2;

draw(A--B--C--cycle);
draw(C--D);

label("$A$", A, NW);
label("$B$", B, SE);
label("$C$", C, SW);
label("$D$", D, NE);

따라서, 삼각형 ACD의 넓이는 (1/2) · AD · CD = (1/2) · (64 / 17) · (120 / 17) = 3840 / 289.

답) 3840 / 289

131

문제) 어떤 정수 n이 0 ≤ n < 18을 만족하고, n ≡ -11213141 (mod 18)일 때, n의 값을 구하시오.

풀이) 정수가 18로 나누어 떨어지려면, 그 자리수의 합이 9로 나누어 떨어지고 마지막 자리가 짝수여야 합니다 (즉, 9와 2로 모두 나누어 떨어져야 합니다). -11213141의 자리수의 합은 14입니다. -11213141은 음수이므로, 이 숫자는 9의 배수보다 5 작습니다. 이 숫자는 9의 배수보다 4 큽니다. 4를 빼면 다음과 같습니다: -11213141 = -11213145 + 4. -11213145의 자리수의 합은 18이므로, 이 숫자는 9의 배수입니다. 그러나 이는 18의 배수가 아니므로 9를 다시 빼야 합니다: -11213141 = -11213154 + 13. 이제 숫자 -11213154는 18의 배수이므로, 답은 13입니다. -11213141 ≡ 13 (mod 18).

답) 13

132

문제) 함수 f(x) = ax⁴ - bx² + x + 5이고, f(-3) = 2일 때, f(3)의 값을 구하세요.

풀이) x = 3과 x = -3에 대해 f(x)를 계산하면 다음과 같습니다. f(3) = a · 3⁴ - b · 3² + 3 + 5, f(-3) = a · (-3)⁴ - b · (-3)² - 3 + 5. 두 번째 식을 첫 번째 식에서 빼면, 대부분의 항이 상쇄되고 다음과 같은 결과를 얻습니다. f(3) - f(-3) = 3 - (-3) = 6. 따라서, f(-3) = 2라면, f(3) = f(-3) + 6 = 2 + 6 = 8입니다.

답) 8

133

문제) Rick는 14의 양의 인수를 생각하고 있고, Steve는 42의 양의 인수를 생각하고 있습니다. Rick과 Steve가 같은 숫자를 생각하고 있다면, 그들이 생각할 수 있는 가능한 숫자는 몇 개입니까?

풀이) 14의 양의 인수를 찾기 위해 14를 곱하는 쌍을 찾습니다. 목록을 다음과 같이 시작합니다: 1, ..., 14. 2를 확인하면, 2 · 7 = 14이므로 목록은 1, 2, ..., 7, 14가 됩니다. 3, 4, 5, 6을 확인하면, 이들은 14의 인수가 아니므로 최종 목록은 1, 2, 7, 14입니다. 다음으로, 42의 인수를 찾기 위해 같은 방법을 사용합니다. 목록을 다음과 같이 시작합니다: 1, ..., 42. 2를 확인하면, 2 · 21 = 42이므로 목록은 1, 2, ..., 21, 42가 됩니다. 3을 확인하면, 3 · 14 = 42이므로 목록은 1, 2, 3, ..., 14, 21, 42가 됩니다. 4와 5를 확인하면, 이들은 42의 인수가 아닙니다. 6을 확인하면, 6 · 7 = 42이므로 목록은 1, 2, 3, 6, ..., 7, 14, 21, 42가 됩니다. 7은 이미 목록에 있으므로 최종 목록은 1, 2, 3, 6, 7, 14, 21, 42입니다. 14의 인수와 42의 인수를 비교하면, 14와 42가 공유하는 인수는 1, 2, 7, 14입니다. 따라서 Rick과 Steve는 4개의 가능한 숫자를 생각할 수 있습니다. 참고로, 14는 42의 인수이므로 14의 모든 인수는 42의 인수이기도 합니다.

답) 4

134

문제) 볼록 사각형에서 가장 큰 각의 크기는 가장 작은 각의 크기의 두 배이며, 나머지 두 각은 모두 직각입니다. 가장 큰 각의 크기는 몇 도입니까?

풀이) 사각형의 내각의 합은 360도여야 합니다. (이것은 공식 S = (n-2) × 180을 사용하여 구할 수 있으며, 여기서 S는 내각의 합이고 n은 다각형의 변의 수입니다. 그러나 이 문제를 빠르게 해결하려면 이 값을 암기하는 것이 좋습니다.) 두 각이 직각이므로 나머지 두 각의 합은 180도가 되어야 합니다. 작은 각을 x라고 하면, 큰 각은 작은 각의 두 배이므로 3x = 180이 됩니다. 따라서 x = 60이고, 2x = 120입니다. 따라서 큰 각은 120도입니다.

답) 120

135

문제) 점 F₁ = (10, 2)와 F₂ = (-16, 2)가 주어져 있습니다. 점 P에 대해 |PF₁ - PF₂| = 24를 만족하는 점들의 집합은 쌍곡선을 형성합니다. 이 쌍곡선의 방정식은 (x - h)² / a² - (y - k)² / b² = 1의 형태로 쓸 수 있습니다. h + k + a + b를 구하세요.

풀이) 쌍곡선의 중심은 선분 F₁F₂의 중점으로, 이는 (-3, 2)입니다. 따라서 h = -3이고 k = 2입니다. 또한, 2a = 24이므로 a = 12입니다. 초점 사이의 거리는 2c = 26이므로 c = 13입니다. 따라서 b² = c² - a² = 169 - 144 = 25이므로 b = 5입니다. 따라서 h + k + a + b = (-3) + 2 + 12 + 5 = 16입니다.

답) 16

136

문제) 42! (42 팩토리얼)의 끝에 있는 0의 개수는 몇 개입니까? (참고: 숫자 n!은 1부터 n까지의 정수의 곱입니다. 예를 들어, 5! = 5 · 4 · 3 · 2 · 1 = 120입니다.)

풀이) 숫자의 끝에 0이 생기려면 그 숫자가 10의 인수를 가져야 하므로, 이 문제는 사실 42!의 소인수 분해에서 10이 몇 번 나타나는지를 묻는 것입니다. 10 = 2 · 5이므로, 각각이 몇 번 나타나는지를 세어야 합니다. 2의 개수가 5의 개수보다 많을 것이므로, 실제로는 5가 소인수 분해에 몇 번 나타나는지만 세면 됩니다. 숫자가 5의 배수일 때마다 소인수 분해에 5의 인수가 추가됩니다. 1부터 42까지 5의 배수는 8개가 있습니다. 이제 25를 살펴보겠습니다. 25는 실제로 5의 인수를 두 개 가지고 있습니다. 이미 하나를 셌으므로, 이제 하나를 더 세어야 합니다. 따라서 5의 인수는 총 8 + 1 = 9번 나타나므로, 42!의 끝에는 9개의 0이 있습니다.

답) 9

137

문제) 양의 실수 수열 (a₁, a₂, ..., aₙ)이 주어져 있습니다. 다음 조건을 만족합니다. ∑_{i=1 to n} a_i = 96, ∑_{i=1 to n} aᵢ² = 144, ∑_{i=1 to n} aᵢ³ = 216. 모든 가능한 n의 값을 더한 값을 구하세요.

풀이) 코시-슈바르츠 부등식에 의해, (a₁ + a₂ + ... + aₙ)(a₁³ + a₂³ + ... + aₙ³) ≥ (a₁² + a₂² + ... + aₙ²)². 96 · 216 = 144²이므로, 코시-슈바르츠 부등식에서 등호가 성립합니다. 이는 a₁³ / a₁ = a₂³ / a₂ = ... = aₙ³ / aₙ을 의미합니다. 따라서 a₁² = a₂² = ... = aₙ²이므로, a₁ = a₂ = ... = aₙ입니다. 주어진 조건에서, na₁ = 96이고 na₁² = 144입니다. 이 두 식을 나누면 a₁ = 3 / 2가 되므로, n = 64입니다.

답) 64

138

문제) 다섯 진수로 413₅ div 2₅의 몫을 표현하세요.

풀이) 다섯 진수에서 10진수와 마찬가지로 나눗셈을 수행할 수 있습니다. 아래와 같이 계산합니다.

몫은 204₅입니다. 위 계산에서 13₅를 2₅로 나누면 4₅가 되는데, 이는 4₅×2₅=8₁₀=13₅이기 때문입니다.

답) 204₅

139

문제) 밥과 앨리스는 각각 파란색, 초록색, 주황색, 빨간색, 보라색 공이 하나씩 들어 있는 가방을 가지고 있습니다. 앨리스는 자신의 가방에서 무작위로 공 하나를 선택하여 밥의 가방에 넣습니다. 그런 다음 밥은 자신의 가방에서 무작위로 공 하나를 선택하여 앨리스의 가방에 넣습니다. 이 과정을 거친 후 두 가방의 내용물이 동일할 확률은 얼마입니까?

풀이) 앨리스가 공을 밥의 가방에 넣은 후, 밥의 가방에는 한 색상의 공이 두 개, 나머지 색상의 공이 각각 하나씩 총 여섯 개의 공이 들어 있습니다. 밥이 공을 선택하여 앨리스의 가방에 넣은 후, 두 가방의 내용물이 동일해지려면 밥이 같은 색상의 두 공 중 하나를 선택해야 합니다. 밥이 선택할 때 가방에는 여섯 개의 공이 있으므로, 같은 색상의 공을 선택할 확률은 2/6 = 1/3 입니다.

답) 1/3

140

문제) 다음 함수의 최대값을 구하세요: f(x, y) = x √(1 - y²) + y √(1 - x²), 여기서 -1 ≤ x, y ≤ 1.

풀이) a와 b를 실수라고 하자. 그러면 (a - b)² ≥ 0이며, 이는 다음과 동등합니다: ab ≤ (a² + b²) / 2. (이는 AM-GM과 비슷하지만, 여기서는 비음수가 아닌 모든 실수에 대해 성립함을 보이고자 합니다.) a = x, b = √(1 - y²)로 설정하면, x √(1 - y²) ≤ (x² + 1 - y²) / 2. a = y, b = √(1 - x²)로 설정하면, y √(1 - x²) ≤ (y² + 1 - x²) / 2. 따라서, x √(1 - y²) + y √(1 - x²) ≤ (x² + 1 - y²) / 2 + (y² + 1 - x²) / 2 = 1. f(1, 0) = 1이므로, 최대값은 1입니다.

답) 1

141

문제) 양의 정수 n이 주어졌을 때, gcd(n + 7, 2n + 1)의 최댓값은 무엇입니까?

풀이) d = gcd(n + 7, 2n + 1)라고 합시다. 그러면 d는 n + 7과 2n + 1을 모두 나눕니다. 따라서 d는 2(n + 7) - (2n + 1) = 13도 나눕니다. 그러므로 d는 최대 13입니다. n = 6일 때, gcd(n + 7, 2n + 1) = gcd(13, 13) = 13이므로 13의 값이 가능합니다. 따라서 gcd(n + 7, 2n + 1)의 최댓값은 13입니다.

답) 13

142

문제) Zach는 세 개의 가방과 여러 개의 연필을 가지고 있습니다. 그는 각 가방에 가능한 한 많은 연필을 넣되, 각 가방에 같은 수의 연필을 넣으라는 지시를 받았습니다. 남길 수 있는 연필의 최대 개수는 얼마입니까?

풀이) Zach가 3개 이상의 연필을 남겼다면, 각 가방에 연필을 하나씩 더 넣을 수 있습니다. 따라서 Zach는 최대 2개의 연필을 남길 수 있습니다.

답) 2

143

문제) 상원 위원회에는 5명의 민주당원, 5명의 공화당원, 1명의 무소속이 있습니다. 각 당의 모든 구성원이 서로 옆에 앉아야 한다면, 그들이 원형 테이블에 앉을 수 있는 방법은 몇 가지입니까? (두 가지 배치는 하나가 다른 하나의 회전인 경우 동등하다고 간주합니다.)

풀이) 무소속이 앉을 자리를 선택합니다. 테이블을 회전할 수 있으므로 어느 자리를 선택하든 상관없습니다. 무소속의 자리가 선택되면, 모든 민주당원이 왼쪽에 앉고 모든 공화당원이 오른쪽에 앉거나 그 반대로 앉을 수 있습니다. 어느 경우든 민주당원을 앉히는 방법은 5! 가지가 있고, 공화당원을 앉히는 방법도 5! 가지가 있습니다. 따라서 테이블 주위에 사람들을 앉히는 총 방법의 수는 2 × 5! × 5! = 2 × 120 × 120 = 28800 가지입니다.

답) 28800

144

문제) 점 O, A, B는 다음을 만족합니다:

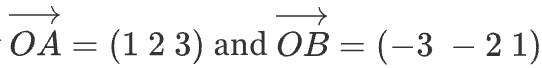
삼각형 OAB의 넓이를 구하세요.

풀이) 벡터 OA 와 OB 에 의해 생성된 평행사변형의 넓이는 다음과 같습니다.

아래는 도형을 그리는 코드입니다.

unitsize(0.4 cm);

pair A, B, C, D;

A = (0,0);
B = (7,2);
C = (1,3);
D = B + C;

draw(A--B,Arrow(6));
draw(A--C,Arrow(6));
draw(B--C);
draw(B--D--C,dashed);

label("$O$", A, SW);
label("$A$", B, SE);
label("$B$", C, W);

따라서, 삼각형 OAB의 넓이는 3√(5)입니다.

답) 3√(5)

145

문제) 곡선은 다음과 같이 매개변수화됩니다: (x, y) = (t³ + 7, -3t² - 6t - 5). 곡선이 t = 2일 때 지나는 점을 찾으세요.

풀이) t = 2일 때, (x, y) = (2³ + 7, -3 · 2² - 6 · 2 - 5) = (15, -29)입니다.

답) (15, -29)

146

문제) 복소수 z에 대해 다음을 만족한다고 하자: z + 1/z = (1 + √(5)) / 2. 다음을 구하시오: z⁸⁵ + 1 / z⁸⁵.

풀이) z + 1/z = (1 + √(5)) / 2에서 z + 1/z - 1/2 = √(5) / 2. 양변을 제곱하면 z² - z + 9/4 - 1/z + 1/z² = 5/4. 따라서 z² - z + 1 - 1/z + 1/z² = 0. 그러므로, z⁴ - z³ + z² - z + 1 = 0. 그렇다면 (z + 1)(z⁴ - z³ + z² - z + 1) = 0, 이를 전개하면 z⁵ + 1 = 0이 됩니다. 이는 z⁵ = -1을 의미합니다. 따라서, z⁸⁵ + 1 / z⁸⁵ = (z⁵)¹⁷ + 1 / (z⁵)¹⁷ = (-1)¹⁷ + 1/(-1)¹⁷ = -2.

답) -2

147

문제) 다음을 간단히 하세요: 3 / √(27)

풀이) 다음과 같이 계산합니다: 3 / √(27) = 3√(3) / √(81) = 3√(3) / 9 = √(3) / 3.

답) √(3) / 3

148

문제) 양의 실수인 x, y, z가 주어져 있고, xyz = 2일 때, 다음 식의 최소값을 구하세요. x⁴ + 4y² + 4z⁴

풀이) AM-GM 부등식을 사용하여, x⁴ + 4y² + 4z⁴ = x⁴ + 2y² + 2y² + 4z⁴ ≥ 4√((x⁴)(2y²)(2y²)(4z⁴)) = 8xyz = 16. 평등은 x⁴ = 2y² = 4z²일 때 발생합니다. 조건 xyz = 2를 사용하여 풀면 x = y = √2이고 z = 1이므로 최소값은 16입니다.

답) 16

149

문제) 다음 방정식을 x에 대해 푸세요: 2 / 3 = 4 / (x - 5).

풀이) 양변에 x - 5와 3을 곱하면 2(x - 5) = 4 × 3이 됩니다. 왼쪽을 전개하면 2x - 10 = 12가 됩니다. 양변에 10을 더하면 2x = 22가 되고, 2로 나누면 x = 11이 됩니다.

답) 11

150

문제) 로사의 나이를 2, 3, 4 또는 6으로 나누면 나머지가 1입니다. 그녀의 나이를 7로 나누면 나머지가 0입니다. 그녀의 나이는 75세 미만입니다. 로사는 몇 살입니까?

풀이) 그녀의 나이를 7로 나누었을 때 나머지가 0이므로, 그녀의 나이는 7의 배수여야 합니다. 나이를 n이라고 하면, n-1은 2, 3, 4, 6의 배수여야 합니다. 이 숫자들의 최소공배수는 12이므로, n-1은 12의 배수여야 합니다. 75보다 작은 12의 배수는 12, 24, 36, 48, 60입니다. 여기에 1을 더하면 13, 25, 37, 49, 61이 되며, 이 중 49만이 7의 배수입니다. 따라서 로사는 49세입니다. 또는 2, 3, 4, 6으로 나누어지지 않는 7의 배수를 찾습니다. 먼저 75보다 작은 7의 홀수 배수를 나열하면 7, 21, 35, 49, 63입니다. 21과 63은 3의 배수이므로, 7, 35, 49가 남습니다. 이 중 49만이 2, 3, 4, 6으로 나누었을 때 나머지가 1입니다.

답) 49

151

문제) 모든 양의 정수 n에 대해, mod₅ (n) 는 n을 5로 나눈 나머지입니다. 함수 f: {0,1,2,3,dots} × {0,1,2,3,4} to {0,1,2,3,4} 를 다음과 같이 재귀적으로 정의합니다:

f(2015,2)는 무엇입니까?

풀이) f(i,j)의 값을 위한 표를 구성합니다.

따라서 f(i,2) = 1 (i ≥ 5일 때)입니다.

답) 1

152

문제) 실수 x₁, x₂, x₃, y₁, y₂, y₃에 대해 다음 조건이 주어집니다. (x₁ - x₂)² + (y₁ - y₂)² = 9, (x₁ - x₃)² + (y₁ - y₃)² = 16, (x₂ - x₃)² + (y₂ - y₃)² = 25. 다음 행렬식의 제곱을 구하세요: det | x₁ y₁ 1 | | x₂ y₂ 1 | | x₃ y₃ 1 |².

풀이) 일반적으로, 1/2 det | x₁ y₁ 1 | | x₂ y₂ 1 | | x₃ y₃ 1 | 는 꼭짓점이 (x₁, y₁), (x₂, y₂), (x₃, y₃)인 삼각형의 부호 있는 넓이입니다. (삼각형의 방향에 따라 넓이는 양수 또는 음수가 될 수 있습니다.) 여기서 삼각형의 변의 길이는 3, 4, 5로, 직각삼각형입니다. 따라서 넓이는 1/2 · 3 · 4 = 6입니다. 그러므로 det | x₁ y₁ 1 | | x₂ y₂ 1 | | x₃ y₃ 1 | = ±12 따라서 det | x₁ y₁ 1 | | x₂ y₂ 1 | | x₃ y₃ 1 |² = 144.

답) 144

153

문제) 삼각형 ABC의 중선 AD, BE, CF는 무게중심 G에서 만납니다. G를 지나는 BC와 평행한 직선이 AB와 AC를 각각 M과 N에서 만납니다. 삼각형 ABC의 넓이가 144일 때, 삼각형 ENG의 넓이를 구하세요.

풀이) E는 AC의 중점이므로, 삼각형 BCE의 넓이는 삼각형 ABC의 넓이의 절반입니다. 따라서 144 / 2 = 72입니다. 아래는 도형을 그리는 코드입니다.

import geometry;

unitsize(1 cm);

pair A, B, C, D, E, F, G, M, N;

A = (1,3);
B = (0,0);
C = (4,0);
D = (B + C)/2;
E = (C + A)/2;
F = (A + B)/2;
G = (A + B + C)/3;
M = extension(G, G + B - C, A, B);
N = extension(G, G + B - C, A, C);

draw(A--B--C--cycle);
draw(A--D);
draw(B--E);
draw(C--F);
draw(M--N);

label("$A$", A, dir(90));
label("$B$", B, SW);
label("$C$", C, SE);
label("$D$", D, S);
label("$E$", E, NE);
label("$F$", F, NW);
label("$G$", G, SSW);
label("$M$", M, NW);
label("$N$", N, NE);

GN은 BC와 평행하므로, 삼각형 ENG와 ECB는 닮음입니다. 또한, G는 삼각형 ABC의 무게중심이므로 닮음비는 EG / EB = 1/3입니다. 따라서 삼각형 ENG의 넓이는 72 × (1/3)² = 8입니다.

답) 8

154

문제) 아래는 도형을 그리는 코드입니다.

size(50);
for (int i=0; i<3; ++i) {
for (int j=0; j<3; ++j) {
dot((i,j));};}

그리드에서 세 점의 집합을 무작위로 선택합니다. 각 세 점 집합은 동일한 확률로 선택됩니다. 세 점이 동일한 직선 위에 있을 확률은 얼마입니까?

풀이) 9개의 그리드 점에서 세 점 집합을 선택할 수 있는 경우의 수는 다음과 같습니다. 9C3 = 9! / (3! · 6!) = 84. 이 중 8개의 집합은 세 점이 일직선상에 있는 경우입니다: 3개의 집합은 수직선상에, 3개의 집합은 수평선상에, 2개의 집합은 대각선상에 있습니다. 따라서 확률은 8 / 84 = 2 / 21입니다.

답) 2 / 21

155

문제) 도마뱀이 길이 12피트, 너비 10피트, 높이 8피트인 방에 있습니다. 도마뱀은 현재 측면 벽(10피트 x 8피트)에 있으며, 천장에서 1피트, 뒷벽(12피트 x 8피트)에서 1피트 떨어져 있습니다. 도마뱀은 반대쪽 측면 벽에서 바닥에서 1피트, 앞벽에서 1피트 떨어진 곳에 있는 파리를 발견했습니다. 도마뱀이 점프하지 않고 천장과 벽을 가로질러 걸을 수 있다고 가정할 때, 도마뱀이 파리에 도달할 수 있는 가장 짧은 경로의 길이는 얼마입니까? 답을 가장 간단한 근호 형태로 표현하세요.

풀이) 아래는 도형을 그리는 코드입니다.

import three;
currentprojection=orthographic(1/2,-1,1/2);
triple A,B,C,D,E,F,G,H,g,f;
A = (0,0,0);
B = (12,0,0);
C = (12,10,0);
D = (0,10,0);
E = (0,10,8);
F = (0,0,8);
G = (12,0,8);
H = (12,10,8);
draw(A--B--C--D--cycle);
draw(E--F--G--H--cycle);
draw(A--F); draw(B--G); draw(C--H); draw(D--E);
g = (12,9,7); f = (0,1,1);
dot(g, green); dot(f, purple);
label("12", A--B); label("10", B--C); label("8", C--H);

위의 다이어그램에서, 녹색 점은 도마뱀이고 보라색 점은 파리입니다. 도마뱀이 이동한 벽을 '펼쳐서' 2차원으로 표현할 수 있습니다. 이 펼침은 도마뱀의 경로 길이를 변경하지 않으므로, 펼치기 전 경로가 최소라면 펼친 후에도 최소여야 합니다. 즉, 펼친 후에는 직선이어야 합니다. 이제 측면 벽 외에도 도마뱀은 앞벽, 뒷벽, 천장을 따라 이동할 수 있습니다. 이 중 앞벽만 따라 이동한다고 가정합시다. 도마뱀이 걸은 벽은 다음과 같이 펼쳐집니다.

draw( (0,0)--(10,0)--(10,8)--(0,8)--cycle ); draw( (10,0)--(22,0) ); draw( (10,8)--(22,8) );
draw( (22,0)--(32,0)--(32,8)--(22,8)--cycle );
pair g = (31,7); pair f = (9,1);
dot(g, green); dot(f, purple);
draw(g--f, red);
draw(f--(31,1), red+dashed); draw(g--(31,1), red+dashed);
label( "10", (0,0)--(10,0) ); label( "12", (10,0)--(22,0) ); label( "10", (22,0)--(32,0) ); label( "8", (32,0)--(32,8) );

도마뱀의 경로는 직각삼각형의 빗변으로, 변의 길이는 6과 22입니다. 따라서 경로의 길이는 √(6² + 22²) = 2√(3² + 11²) = 2√130입니다. 대칭적으로(도마뱀과 파리는 방에서 정확히 반대편에 위치), 도마뱀이 뒷벽과 측면 벽만 따라 이동해도 경로 길이는 동일합니다. 이제 도마뱀이 천장과 측면 벽만 따라 이동한다고 가정합시다. 이 벽들은 다음과 같이 펼쳐집니다.

draw( (0,0)--(8,0)--(8,10)--(0,10)--cycle ); draw( (8,0)--(20,0) ); draw( (8,10)--(20,10) );
draw( (20,0)--(28,0)--(28,10)--(20,10)--cycle );
pair g = (21,9); pair f = (1,1);
dot(g, green); dot(f, purple);
draw(g--f, red);
draw(f--(21,1), red+dashed); draw(g--(21,1), red+dashed);
label( "8", (0,0)--(8,0) ); label( "12", (8,0)--(20,0) ); label( "8", (20,0)--(28,0) ); label( "10", (28,0)--(28,10) );

경로는 직각삼각형의 빗변으로, 변의 길이는 8과 20입니다. 따라서 경로의 길이는 √(8² + 20²) = 2√(4² + 10²) = 2√116입니다. (비교를 쉽게 하기 위해 이 형태로 유지합니다.) 마지막으로, 도마뱀이 천장과 앞벽(또는 뒷벽; 대칭적으로 동일한 결과를 줍니다)을 가로지를 수 있습니다. 펼친 벽은 다음과 같습니다.

draw( (0,0)--(10,0)--(10,8)--(0,8)--cycle );
draw( (10,0)--(22,0)--(22,8)--(10,8)--(10,18)--(22,18) );
draw( (22,8)--(30,8)--(30,18)--(22,18)--cycle );
pair g = (23,17); pair f = (9,1);
dot(g, green); dot(f, purple);
draw(g--f, red);
draw(f--(23,1), red+dashed); draw(g--(23,1), red+dashed);
label("10", (0,0)--(10,0)); label("12", (10,0)--(22,0)); label("8", (0,0)--(0,8), W);

label("8", (22,18)--(30,18), N); label("10", (30,18)--(30,8), E);

경로는 직각삼각형의 빗변으로, 변의 길이는 16과 14입니다. 따라서 경로의 길이는 √(16² + 14²) = 2√(8² + 7²) = 2√113입니다. 세 가지 경우 중 가장 짧은 경로이므로, 답은 2√113입니다.

답) 2√113

156

문제) 점 (x, y)가 0 ≤ x ≤ 8 및 0 ≤ y ≤ 4를 만족하도록 무작위로 선택됩니다. x + y ≤ 4일 확률은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) x + y ≤ 4를 y ≤ 4 - x로 다시 작성합니다. 이 부등식은 y = 4 - x 직선 위와 아래의 점들에 의해 만족됩니다. 이 직선과 0 ≤ x ≤ 8 및 0 ≤ y ≤ 4 부등식에 의해 결정된 4 × 8 직사각형을 스케치하면, x + y ≤ 4를 만족하는 점들은 음영이 있는 삼각형 안에 있는 점들입니다 (그림 참조). 삼각형의 면적은 1/2 × 4 × 4 = 8 제곱 단위이고, 직사각형의 면적은 4 × 8 = 32 제곱 단위이므로, 무작위로 선택된 점이 음영이 있는 삼각형에 속할 확률은 1/4입니다.

import graph; size(200); defaultpen(linewidth(0.7)+fontsize(10));

dotfactor=4;

real f(real x) { return 4-x; }

pair A=(0,4), B=(8,4), C=(8,0), D=(0,0); pair[] dots={A,B,C,D};

fill(A--(4,0)--D--cycle,gray(0.7)); draw(A--B--C);

xaxis(xmin=-3,xmax=9,Ticks(" ",1.0, begin=false, end=false, NoZero, Size=3), Arrows(4), above=true);

yaxis(ymin=-1,ymax=5,Ticks(" ",1.0,begin=false, end=false, NoZero, Size=3), Arrows(4), above=true);

draw(graph(f,-0.8,4.5),Arrows(4)); label("$x+y=4$",(-2.2,5.2));

답) 1/4

157

문제) 두 주자 A와 B가 선형 트랙의 점 O에서 같은 방향으로 달리기 시작합니다. 주자 B는 주자 A보다 세 배 빠르게 달립니다. 관찰자는 트랙에 수직인 선 OP가 있는 점 P에 서 있습니다. ∠APB 의 최대값을 도 단위로 구하세요. 아래는 도형을 그리는 코드입니다.

unitsize(2 cm);

pair A, B, O, P;

A = (0.4,0);
B = (1.2,0);
O = (0,0);
P = (0,1);

draw((-0.5,0)--(2,0));
draw(O--P);
draw(P--A);
draw(P--B);

label("$A$", A, S);
label("$B$", B, S);
label("$O$", O, S);
label("$P$", P, N);

풀이) 일반성을 잃지 않고, OP = 1이라고 가정합니다. OA = x이고 OB = 3x라고 합시다. α = ∠OPA 이고 β = ∠OPB 라고 하면, tan α = x 이고 tan β = 3x 입니다. 각도 차이 공식을 사용하면, tan ∠APB = tan (∠OPB - ∠OPA) = tan (β - α) = tan β - tan α / 1 + tan α tan β = 2x / 1 + 3x² 이 표현을 최대화하려고 합니다. 이 표현을 최대화하는 것은 1 + 3x² / 2x 를 최소화하는 것과 같습니다. AM-GM 부등식에 의해, 1 + 3x² / 2x ≥ 2 √(1 · 3x²) / 2x = 2x √(3) / 2x = √(3) 따라서 tan ∠APB ≤ 1 / √(3) 이는 ∠APB ≤ 30° 를 의미합니다. x = 1 / √(3) 일 때 평등이 성립하므로, ∠APB 의 최대값은 30° 입니다.

답) 30°

158

문제) 다항식의 근인 a, b, c에 대해 a + b + c를 구하세요. 주어진 방정식은 다음과 같습니다: 1/x + 5x² = 6x - 24.

풀이) 비에타의 정리를 적용하고 싶지만, 주어진 방정식은 1/x 항 때문에 다항식 방정식이 아닙니다. 이 방정식을 동등한 다항식 방정식으로 바꾸기 위해 양변에 x를 곱하고 정리합니다: 1 + 5x³ = 6x² - 24x 5x³ - 6x² + 24x + 1 = 0 이제 비에타의 정리를 사용할 수 있습니다: 근의 합은 a + b + c = 6/5 입니다.

답) 6/5

159

문제) 100과 200 사이의 7의 배수의 합은 얼마입니까?

풀이) 100과 200 사이의 7의 배수 중 가장 작은 수는 105이고, 가장 큰 수는 196입니다. 따라서 우리는 등차수열 105 + 112 + ... + 196의 합을 구해야 합니다. 이 등차수열의 n번째 항은 105 + 7(n - 1) = 7n + 98입니다. 만약 7n + 98 = 196이라면, n = 14이므로 이 수열의 항의 개수는 14개입니다. 등차수열의 합은 첫 번째 항과 마지막 항의 평균에 항의 개수를 곱한 것과 같으므로, 합은 (105 + 196) / 2 · 14 = 2107입니다.

답) 2107

160

문제) 이차식 x² + 2.6x + 3.6을 (x + b)² + c의 형태로 쓸 수 있습니다. 여기서 b와 c는 상수입니다. b + c는 얼마입니까? (소수로 표현하세요)

풀이) 완전제곱식을 만듭니다. (x + 1.3)² = x² + 2.6x + 1.69이므로, x² + 2.6x + 3.6 = (x + 1.3)² - 1.69 + 3.6 = (x + 1.3)² + 1.91. 따라서, b = 1.3이고 c = 1.91이므로 b + c = 3.21입니다.

답) 3.21

161

문제) 두 연속하는 양의 짝수의 곱이 288입니다. 두 수 중 더 큰 수는 무엇입니까?

풀이) 먼저 288의 소인수 분해를 찾으면 2⁵ · 3²입니다. 이 인수들을 두 연속하는 짝수에 나누어야 합니다. 3은 적어도 하나의 2와 함께 있어야 짝수가 되므로, 인수 중 하나는 6의 배수여야 합니다. 여러 시도를 통해, 한 인수가 18일 때 나머지는 2⁴ = 16이 됩니다. 따라서 두 수는 16과 18이며, 더 큰 수는 18입니다.

답) 18

162

문제) 다음을 평가하세요: log₂64.

풀이) 2⁶ = 64이므로, log₂64 = 6입니다.

답) 6

163

문제) 집합 {1, 2, 3, ..., 100}에서 무작위로 선택된 정수가 2로 나누어 떨어지지만 3으로 나누어 떨어지지 않을 확률은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) 100 = 50 × 2이므로, 집합에서 2로 나누어 떨어지는 정수는 50개입니다. 이 중 3으로도 나누어 떨어지는 수는 집합에서 6의 배수입니다. 100을 6으로 나누면 16과 2/3이므로, 집합에는 6의 배수가 16개 있습니다. 따라서 2의 배수이지만 3의 배수가 아닌 수는 50 - 16 = 34개입니다. 집합에는 총 100개의 수가 있으므로, 원하는 확률은 34 / 100 = 17 / 50입니다.

답) 17 / 50

164

문제) 만약 -6 ≤ a ≤ -2이고 3 ≤ b ≤ 5라면, (a+1 / b)(1 / b-a)의 가능한 최대값은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) 주어진 식은 1 / b² - a²로 전개됩니다. 따라서 b의 크기가 가능한 작고 a의 크기도 가능한 작아야 합니다. 최대값은 1 / 3² - (-2)² = -35 / 9입니다.

답) -35/9

165

문제) 다음을 간단히 하세요: tan 100° + 4 sin 100°.

풀이) 우리는 다음과 같이 계산할 수 있습니다. tan 100° + 4 sin 100° = sin 100° / cos 100° + 4 sin 100° = sin 80° / -cos 80° + 4 sin 80° = -cos 10° / sin 10° + 4 cos 10° = (4 cos 10° sin 10° - cos 10°) / sin 10°. 이중각 공식을 사용하면, (4 cos 10° sin 10° - cos 10°) / sin 10° = (2 sin 20° - cos 10°) / sin 10° = (sin 20° + sin 20° - sin 80°) / sin 10°. 합차공식을 사용하면, sin 20° - sin 80° = 2 cos 50° sin (-30°) = -cos 50°, 따라서 (sin 20° + sin 20° - sin 80°) / sin 10° = (sin 20° - cos 50°) / sin 10° = (sin 20° - sin 40°) / sin 10°. 합차공식을 사용하면, sin 20° - sin 40° = 2 cos 30° sin (-10°) = -√3 sin 10°, 따라서 (sin 20° - sin 40°) / sin 10° = -√3입니다.

답) -√3

166

문제) 책장에는 3개의 선반이 있으며 총 24권의 책이 있습니다. 맨 위 선반에는 8권의 추리 소설이 있습니다. 중간 선반에는 10권의 수학 책이 있습니다. 맨 아래 선반에는 6권의 과학 책이 있습니다. 각 선반에서 두 권의 책이 제거되었습니다. 남아 있는 세 선반의 책 중 수학 책의 비율은 얼마입니까? 답을 기약 분수로 표현하세요.

풀이) 선반에서 6권의 책이 제거되었으므로, 24 - 6 = 18권의 책이 남습니다. 이 중 10 - 2 = 8권이 수학 책입니다. 따라서 남아 있는 책 중 수학 책의 비율은 8 / 18 = 4 / 9 입니다.

답) 4 / 9

167

문제) 정사각형과 정칠각형이 같은 평면에 있으며 공통 변 AD 를 공유합니다. ∠BAC 의 도 단위 측정값은 얼마입니까? 답을 일반 분수로 표현하세요. 아래는 도형을 그리는 코드입니다.

for(int i=0; i <=7; ++i) {
draw(dir(360*i/7+90)--dir(360*(i+1)/7+90));
}
pair A = dir(360*3/7+90);
pair F = dir(360*4/7+90);
pair C = A+dir(90)*(F-A);
pair D = C+F-A;
pair B = dir(360*2/7+90);

draw(A--C--D--F);

label("$A$",A,S);
label("$B$",B,W);
label("$C$",C,SE);
label("$D$",F,S);

풀이) 정n각형의 각 내부 각도는 180(n-2)/n 도입니다. 따라서, ∠BAD 의 크기는 180(7-2)/7 = 900/7°이고, ∠CAD 는 90°입니다. 이들의 차이인 ∠BAC 는 900/7 - 630/7 = 270/7°입니다.

답) 270/7°

168

문제) 원뿔의 부피는 공식 V = (1/3)Bh로 주어집니다. 여기서 B는 밑면의 넓이이고, h는 높이입니다. 원뿔의 밑면의 넓이가 30 제곱 단위이고, 높이가 6.5 단위일 때, 부피는 몇 세제곱 단위입니까?

풀이) B = 30이고 h = 6.5일 때, (1/3)Bh를 구해야 합니다. 계산하면, (1/3)Bh = (1/3)(30)(6.5) = (10)(6.5) = 65입니다.

답) 65

169

문제) 세 가지 크기의 정사각형이 총 70개 있으며, 이 정사각형의 꼭짓점은 이 직사각형 3× n 격자의 점들입니다. n의 값은 얼마입니까? 아래는 도형을 그리는 코드입니다.

unitsize(0.4 inch);

dot((0,0),linewidth(9bp));
dot((1,0),linewidth(9bp));
dot((2,0),linewidth(9bp));
dot((0,1),linewidth(9bp));
dot((0,2),linewidth(9bp));
dot((1,1),linewidth(9bp));
dot((2,1),linewidth(9bp));
dot((1,2),linewidth(9bp));
dot((2,2),linewidth(9bp));

filldraw((2.95,-0.05)--(3.05,-0.05)--(3.05,0.05)--(2.95,0.05)--cycle,black);
filldraw((2.45,-0.05)--(2.55,-0.05)--(2.55,0.05)--(2.45,0.05)--cycle,black);
filldraw((3.45,-0.05)--(3.55,-0.05)--(3.55,0.05)--(3.45,0.05)--cycle,black);

filldraw((2.95,0.95)--(3.05,0.95)--(3.05,1.05)--(2.95,1.05)--cycle,black);
filldraw((2.45,0.95)--(2.55,0.95)--(2.55,1.05)--(2.45,1.05)--cycle,black);
filldraw((3.45,0.95)--(3.55,0.95)--(3.55,1.05)--(3.45,1.05)--cycle,black);

filldraw((2.95,1.95)--(3.05,1.95)--(3.05,2.05)--(2.95,2.05)--cycle,black);
filldraw((2.45,1.95)--(2.55,1.95)--(2.55,2.05)--(2.45,2.05)--cycle,black);
filldraw((3.45,1.95)--(3.55,1.95)--(3.55,2.05)--(3.45,2.05)--cycle,black);

dot((4,0),linewidth(9bp));
dot((5,0),linewidth(9bp));
dot((4,1),linewidth(9bp));
dot((5,1),linewidth(9bp));
dot((4,2),linewidth(9bp));
dot((5,2),linewidth(9bp));

풀이) 도형에서 1×1 정사각형의 개수는 2(n-1)이고, 2×2 정사각형의 개수는 n-2이며, √2 × √2 정사각형의 개수도 n-2입니다 (도형 참조). 다음 식을 풀면: 2(n-1) + n-2 + n-2 = 70 n = 19임을 알 수 있습니다. 아래는 도형을 그리는 코드입니다.

unitsize(5mm);
defaultpen(linewidth(.7pt)+fontsize(8pt));
dotfactor=4;

int i,j;

for(i=0;i<=10;i=i+1)
  for(j=0;j<=2;j=j+1){
    dot((i,j));
  }

draw((0,0)--(1,0)--(1,1)--(0,1)--cycle);
draw((3,0)--(5,0)--(5,2)--(3,2)--cycle);
draw((7,1)--(8,2)--(9,1)--(8,0)--cycle);

답) 19

170

문제) 한 변의 길이가 5, 5, 6인 삼각형의 넓이는 몇 제곱 단위입니까?

풀이) 이 삼각형은 이등변 삼각형이므로, 길이가 6인 변에 대한 높이는 그 변의 중점에 닿아야 합니다. 따라서 이 삼각형은 빗변이 5이고 한 변의 길이가 3인 두 개의 직각삼각형으로 나뉩니다. 각각은 3-4-5 삼각형이며, 각각의 넓이는 3 × 4 / 2 = 6입니다. 따라서 전체 넓이는 12입니다.

답) 12

171

문제) 두 방정식 y = x² - 8과 y² = -5x + 44의 모든 서로 다른 해 (x, y)의 y 좌표의 곱을 구하세요.

풀이) 방정식 y = x² - 8을 제곱하면 y² = x⁴ - 16x² + 64가 됩니다. 오른쪽 항을 같게 설정하면 다음과 같습니다: -5x + 44 = x⁴ - 16x² + 64 ⇔ 0 = x⁴ - 16x² + 5x + 20 = x²(x² - 16) + 5(x + 4) = x²(x - 4)(x + 4) + 5(x + 4) = (x + 4)(x³ - 4x² + 5). 따라서, 하나의 해는 x 값이 -4입니다. 이제 다항식 x³ - 4x² + 5가 남습니다. 가능한 유리근은 pm1과 pm5입니다. 합성 또는 장제법을 사용하여 (x + 1)이 인수임을 알 수 있습니다: (x + 1)(x² - 5x + 5) = x³ - 4x² + 5 따라서, 하나의 해는 x 값이 -1입니다. x² - 5x + 5는 쉽게 인수분해되지 않으므로, 이차 방정식 공식을 사용하여 x = (5 ± √(25 - 4 · 1 · 5)) / 2 = (5 ± √5) / 2. 네 개의 x 값은 -4, -1, (5 + √5) / 2, (5 - √5) / 2입니다. 각각을 제곱하면: (-4)² = 16 (-1)² = 1 ((5 + √5) / 2)² = (25 + 10√5 + 5) / 4 = (15 + 5√5) / 2 ((5 - √5) / 2)² = (25 - 10√5 + 5) / 4 = (15 - 5√5) / 2 그리고 8을 빼면: 16 - 8 = 8 1 - 8 = -7 (15 + 5√5) / 2 - 8 = (-1 + 5√5) / 2 (15 - 5√5) / 2 - 8 = (-1 - 5√5) / 2 따라서 네 개의 해는 다음과 같습니다: (-4, 8), (-1, -7), ((5 + √5) / 2, (-1 + 5√5) / 2), ((5 - √5) / 2, (-1 - 5√5) / 2). 이제 y 좌표를 곱하면: 8 · -7 · ((-1 + 5√5) / 2) · ((-1 - 5√5) / 2) = -56(1 - 25 · 5) / 4 = 1736.

답) 1736

172

문제) Louis와 Jack은 파이를 나누어 먹고 있습니다. Louis는 파이의 1/5을 먹고, Jack은 파이의 2/3을 먹습니다. Louis와 Jack이 함께 먹은 파이의 양은 얼마입니까?

풀이) 분모 5와 3의 공통 배수는 15입니다. 이를 이용하여 1/5 · 3/3 = 3/15와 2/3 · 5/5 = 10/15로 쓸 수 있습니다. 그런 다음, 분자들을 더하고 분모는 그대로 두어 분수를 더할 수 있습니다. 따라서 1/5 + 2/3 = 3/15 + 10/15 = (3 + 10)/15 = 13/15입니다.

답) 13/15

173

문제) 등차수열의 네 번째 항이 200이고 여덟 번째 항이 500일 때, 여섯 번째 항은 무엇입니까?

풀이) 여섯 번째 항은 등차수열에서 네 번째 항과 여덟 번째 항의 정확히 중간에 위치하므로, 두 항의 평균입니다. 따라서 여섯 번째 항은 (200 + 500) / 2 = 350입니다. 또한, 네 번째 항과 여덟 번째 항 사이에 네 단계가 있다는 점을 이용하여 공차를 구할 수도 있습니다. 공차를 d라고 하면, 4d = 500 - 200 = 300이 됩니다. 따라서 d = 75를 찾을 수 있습니다. 여섯 번째 항은 네 번째 항에서 두 단계 후이므로, 200 + 2d = 350입니다.

답) 350

174

문제) 기하급수 4 + 12 / a + 36 / a² + ···를 고려하세요. 합이 완전제곱수일 때, a가 양의 정수인 경우 가능한 가장 작은 값은 무엇입니까?

풀이) 기하급수의 합을 구하는 공식 첫 번째 항 / 1-(공비)를 사용하여 합을 구하면 4 / 1-3 / a=4 / a-3 / a=4a / a-3입니다. 우리는 4a / a-3가 완전제곱수 b²가 되기를 원합니다. 여기서 b는 양의 정수입니다. 따라서 4a = b²(a-3)이고, 양의 정수 a를 얻을 때까지 b의 값을 시도합니다. b=1일 때, 4a=a-3, 하지만 이는 a=-1을 의미합니다. b=2일 때, 4a=4(a-3) ⇒ 0 = -12. b=3일 때, 4a=9(a-3) ⇒ -5a=-27, 이는 a에 대한 정수 값을 제공하지 않습니다. b=4일 때, 4a=16(a-3) ⇒ -12a=-48, 따라서 a=4, 이는 양의 정수입니다. 또는 무한 기하급수가 수렴하려면 공비가 -1과 1 사이여야 합니다. 따라서 3 / a는 1보다 작아야 하며, 이는 a가 3보다 커야 함을 의미합니다. a=4를 시도하면 4 / 1-3 / 4=4 / 1 / 4=4·4=16, 이는 완전제곱수입니다.

답) 4

175

문제) 포물선 x = y² - 4y - 1의 그래프는 몇 개의 y절편을 가집니까?

풀이) y절편은 그래프가 y축에 놓인 점이므로 x = 0입니다. 따라서, y절편의 개수는 이차 방정식 y² - 4y - 1 = 0의 실수 해의 개수와 같습니다. 이 이차 방정식의 판별식은 (-4)² + 4 · 1 · (-1) = 20으로, 양수이므로 이차 방정식은 두 개의 서로 다른 실근을 가집니다. 따라서, y절편의 개수는 2개입니다. 아래는 도형을 그리는 코드입니다.

size(150);
real ticklen=3;
real tickspace=2;

real ticklength=0.1cm;
real axisarrowsize=0.14cm;
pen axispen=black+1.3bp;
real vectorarrowsize=0.2cm;
real tickdown=-0.5;
real tickdownlength=-0.15inch;
real tickdownbase=0.3;
real wholetickdown=tickdown;
void rr_cartesian_axes(real xleft, real xright, real ybottom, real ytop, real xstep=1, real ystep=1, bool

useticks=false, bool complexplane=false, bool usegrid=true) {

 import graph;

 real i;
 if(complexplane) {
  label("$\textnormal{Re}$",(xright,0),SE);
  label("$\textnormal{Im}$",(0,ytop),NW);
 } else {
  label("$x$",(xright+0.4,-0.5));
  label("$y$",(-0.5,ytop+0.2));
 }

 ylimits(ybottom,ytop);
 xlimits( xleft, xright);
 real[] TicksArrx,TicksArry;

 for(i=xleft+xstep; i<xright; i+=xstep) {
  if(abs(i) >0.1) {
   TicksArrx.push(i);
  }
 }
 for(i=ybottom+ystep; i<ytop; i+=ystep) {
  if(abs(i) >0.1) {
   TicksArry.push(i);
  }
 }

 if(usegrid) {
  xaxis(BottomTop(extend=false), Ticks("%", TicksArrx ,pTick=gray(0.22),extend=true),p=invisible);//,above=true);
  yaxis(leftRight(extend=false),Ticks("%", TicksArry ,pTick=gray(0.22),extend=true),p=invisible);//,Arrows);
 }

 if(useticks) {
  xequals(0, ymin=ybottom, ymax=ytop, p=axispen, Ticks("%",TicksArry, pTick=black+0.8bp,Size=ticklength), above=true, Arrows(size=axisarrowsize));
  yequals(0, xmin=xleft, xmax=xright, p=axispen, Ticks("%",TicksArrx, pTick=black+0.8bp,Size=ticklength), above=true, Arrows(size=axisarrowsize));
 } else {
  xequals(0, ymin=ybottom, ymax=ytop, p=axispen, above=true, Arrows(size=axisarrowsize));
  yequals(0, xmin=xleft, xmax=xright, p=axispen, above=true, Arrows(size=axisarrowsize));
 }
};

real lowerx, upperx, lowery, uppery;
real f(real x) {return x^2 - 4*x - 1;}
lowery = -1;
uppery = 5;
rr_cartesian_axes(-6,5,lowery,uppery);
draw(reflect((0,0),(1,1))*(graph(f,lowery,uppery,operator ..)), red);
dot((0,2 + sqrt(5)));
dot((0,2 - sqrt(5)));

답) 2

176

문제) 정수 m과 n이 3m + 4n = 100을 만족할 때, |m - n|의 가능한 가장 작은 값은 무엇입니까?

풀이) 식 3m + 4n = 100에서 n = 25 - (3/4)m을 얻을 수 있습니다. 그러면 우리는 다음을 최소화하고자 합니다: |m - n| = |m - 25 + (3/4)m| = |(7/4)m - 25| = |7m - 100| 즉, 우리는 7m이 100에 최대한 가깝도록 하면서 3m + 4n = 100의 정수 해를 찾고자 합니다. 시도와 오류를 통해, 3m + 4n = 100의 해 중 m이 100/7에 가장 가까운 값은 (m, n) = (16, 13)임을 알 수 있습니다. 그러면 |m - n| = 16 - 13 = 3입니다.

답) 3

177

문제) 21 / (2² · 5⁷)를 유한 소수로 변환하세요.

풀이) 유한 소수는 a / 10ᵇ 형태로 쓸 수 있습니다. 여기서 a와 b는 정수입니다. 따라서 분모를 10ᵇ 형태로 만들어 봅시다: (21 / (2² · 5⁷)) · (2⁵ / 2⁵) = (21 · 32) / 10⁷ = 672 / 10⁷ = 0.0000672.

답) 0.0000672

178

문제) 도형에서, 중심이 P, Q, R, S인 반지름 1의 네 개의 원이 서로 및 삼각형 ABC의 변에 접해 있습니다. 아래는 도형을 그리는 코드입니다.

size(200);
pair A, B, C, P, Q, R, S;
R=(0,0);
Q=(-2,0);
S=(2,0);
P=(1,1.732);
B=(-5.73,-1);
C=(3.732,-1);
A=(1.366,3.098);
draw(A--B--C--A);
draw(circle(P, 1));
draw(circle(Q, 1));
draw(circle(R, 1));
draw(circle(S, 1));
label("A", A, N);
label("B", B, SW);
label("C", C, SE);
dot(P);
dot(Q);
dot(R);
dot(S);
label("P", P, N);
label("Q", Q, SW);
label("R", R, SW);
label("S", S, SE);

삼각형 PQS에서 가장 작은 각의 크기는 몇 도입니까?

풀이) PQ, PR, PS, RQ, RS를 연결합니다. Q, R, S 중심의 원이 모두 BC에 접해 있으므로, QR과 RS는 각각 BC와 평행합니다 (중심 Q, R, S는 각각 BC 위 1 단위에 있습니다). 이는 QS가 R을 통과한다는 것을 알려줍니다. 접하는 원의 중심을 연결하면, 형성된 선분은 접점과 관련된 점을 통과하며, 그 길이는 해당 원의 반지름의 합과 같습니다. 따라서 QR = RS = PR = PS = 1 + 1 = 2입니다. 아래는 도형을 그리는 코드입니다.

size(200);
pair P, Q, R, S;
Q=(0,0);
R=(2,0);
S=(4,0);
P=(3,1.732);
label("Q", Q, SW);
label("R", R, dir(270));
label("S", S, SE);
label("P", P, N);
draw(circle(Q,1), dashed);
draw(circle(P,1), dashed);
draw(circle(R,1), dashed);
draw(circle(S,1), dashed);
draw(P--Q--S--P--R);

PR = PS = RS이므로, 삼각형 PRS는 정삼각형이며, ∠PSR = ∠PRS = 60°. ∠PRS = 60°이고 QRS는 직선이므로, ∠QRP = 180° - 60° = 120°. QR = RP이므로, 삼각형 QRP는 이등변삼각형이며, ∠PQR = 1/2(180° - 120°) = 30°. ∠PQS = 30°이고 ∠PSQ = 60°이므로, ∠QPS = 180° - 30° - 60° = 90°, 따라서 삼각형 PQS는 30°-60°-90° 삼각형입니다. 따라서 답은 30°입니다.

답) 30°

179

문제) 양수인 10 × 15 × 24의 제곱근은 무엇입니까?

풀이) 다음과 같이 계산할 수 있습니다. √(10 · 15 · 24) = √((2 · 5) · (3 · 5) · (2³ · 3)) = √(2⁴ · 3² · 5²) = 2² · 3 · 5 = 60.

답) 60

180

문제) 점 (0, -1, -1), (-4, 4, 4), (4, 5, 1)을 포함하는 평면의 방정식을 찾으세요. 답을 다음 형태로 입력하세요: Ax + By + Cz + D = 0, 여기서 A, B, C, D는 정수이며 A > 0이고 gcd(|A|, |B|, |C|, |D|) = 1입니다.

풀이) 벡터 a = (0, -1, -1), b = (-4, 4, 4), c = (4, 5, 1) 를 정의합니다. 그러면 평면의 법선 벡터는 다음 두 벡터에 수직입니다: b - a = (-4, 5, 5), c - a = (4, 6, 2). 따라서 법선 벡터를 계산하기 위해 이 벡터들의 외적을 구합니다: (-4, 5, 5) × (4, 6, 2) = (-20, 28, -44). 이 벡터를 스케일링하여 (5, -7, 11) 을 법선 벡터로 사용할 수 있습니다. 그러면 평면의 방정식은 다음과 같은 형태입니다: 5x - 7y + 11z + D = 0. 점 중 하나의 좌표를 대입하여 평면의 방정식을 구하면, 5x - 7y + 11z + 4 = 0이 됩니다.

답) 5x - 7y + 11z + 4 = 0

181

문제) 100과 150의 공약수 중 두 자리 양의 정수는 몇 개입니까?

풀이) 100의 약수는 1, 2, 4, 5, 10, 20, 25, 50, 100입니다. 이 중에서 두 자리 수인 10, 25, 50은 150의 약수이기도 합니다. 따라서 두 자리 공약수는 3개입니다.

답) 3

182

문제) 다음 식을 간단히 하고 유리화된 분모로 결과를 작성하세요: √(³√(√(1 / 729)))

풀이) 먼저, 729 = 3⁶임을 확인합니다. 가장 안쪽의 제곱근부터 간단히 할 수 있습니다: √(³√(1 / √(729))) = √(³√(1 / 27)) = √(1 / 3) = 1 / √(3) = √(3) / 3

답) √(3) / 3

183

문제) 베이커 중학교 학생의 3분의 2가 음악을 듣습니다. 음악을 듣는 학생은 834명입니다. 베이커 중학교에는 총 몇 명의 학생이 있습니까?

풀이) 베이커 중학교에 학생이 S명 있다고 하면, 2/3 S명의 학생이 음악을 듣습니다. 2/3 S를 834와 같다고 설정하고, 양변에 3/2를 곱하면, 학교에는 3/2 × 834 = 1251명의 학생이 있다는 것을 알 수 있습니다.

답) 1251

184

문제) 다음을 dfrac{a√(2) + b√(3)}{c} 형태로 나타내고, a, b, c가 양의 정수이며 c가 가능한 한 작을 때, a+b+c는 얼마입니까? √2 + 1/√2 + √3 + 1/√3

풀이) 공통 분모는 √2 · √3 = √6입니다. 따라서 이 표현은 다음과 같이 됩니다: (√2 · (√2 · √3) + 1 · √3 + √3 · (√2 · √3) + 1 · √2) / √6 이를 정리하면 (2√3 + √3 + 3√2 + √2) / √6 = (4√2 + 3√3) / √6입니다. 유리화하기 위해 분자와 분모에 √6을 곱하면 (4√2√6 + 3√3√6) / 6이 됩니다. 이를 정리하면 (9√2 + 8√3) / 6이 되며, 따라서 원하는 합은 9 + 8 + 6 = 23입니다.

답) 23

185

문제) 양의 실수인 a, b, c가 주어졌을 때, 다음 식의 가능한 모든 값을 구하시오. c / a + a / (b + c) + b / c

풀이) S = c / a + a / (b + c) + b / c 라고 하자. 그러면 S + 1 = c / a + a / (b + c) + b / c + 1 = c / a + a / (b + c) + (b + c) / c. AM-GM 부등식에 의해, S + 1 = c / a + a / (b + c) + (b + c) / c ≥ 3 · ³√(c / a · a / (b + c) · (b + c) / c) = 3. 평등은 c / a = a / (b + c) = (b + c) / c = 1일 때만 성립합니다. b와 c가 양수이므로, (b + c) / c > 1 따라서 평등은 성립할 수 없습니다. 그러므로 S + 1 > 3, 즉 S > 2입니다. S는 2보다 큰 모든 실수 값을 가질 수 있다고 주장합니다. c = a로 두면, S = 1 + a / (b + a) + b / a. b가 0에 가까워질 때, 이 식은 2에 가까워집니다. 이는 이 식을 원하는 만큼 2에 가깝게 만들 수 있음을 의미합니다. 반면, b가 매우 커지면, 이 식도 매우 커집니다. 이는 이 식을 원하는 만큼 크게 만들 수 있음을 의미합니다. 따라서 연속성 논증에 의해, S는 (2, ∞) 범위의 모든 값을 가질 수 있습니다.

답) (2, ∞)

186

문제) 만약 (3ᵏ)⁶ = 3⁶이라면, k를 찾으세요.

풀이) 지수 법칙에 따르면, (3ᵏ)⁶ = 3⁶ᵏ입니다. 3⁶ᵏ = 3⁶이므로, 6k = 6이 됩니다. 이를 6으로 나누면, k = 1입니다.

답) 1

187

문제) 양의 정수 n > 1에 대해 2²⁴가 완전한 n^번째 거듭제곱이 되는 경우는 몇 개입니까?

풀이) 2²⁴가 완전한 n^번째 거듭제곱이 되려면 n이 24의 약수여야 합니다. 24의 약수 중 1보다 큰 것은 2, 3, 4, 6, 8, 12, 24입니다. 따라서 가능한 n의 값은 7개입니다.

답) 7

188

문제) 힐러리는 11개의 동전을 가지고 있으며, 모두 다임과 니켈입니다. 총 동전의 가치는 75센트입니다. 힐러리가 가지고 있는 니켈의 개수는 몇 개입니까?

풀이) 힐러리가 가지고 있는 다임의 수를 d, 니켈의 수를 n이라고 합시다. 다음 두 개의 방정식을 세울 수 있습니다. d + n = 11 10d + 5n = 75 (마지막 방정식은 센트 단위입니다.) 두 번째 방정식을 더 간단하게 만들기 위해 양변을 5로 나누면 2d + n = 15가 됩니다. 첫 번째 방정식에서 d = 11 - n을 얻을 수 있습니다. 이를 두 번째 방정식에 대입하여 d를 제거하면, 2(11 - n) + n = 15가 되어 n = 7이 됩니다. 따라서, 힐러리는 7개의 니켈을 가지고 있습니다.

답) 7

189

문제) 함수 f(x) = exp(3x²-|⎣x⎦!) + _{22+735235|⎣x⎦|}C₂₃₅₆ + φ(|⎣x⎦|+1) + 72x⁴ + 3x³ - 6x² + 2x + 1와 g(x) = exp(3x²-|⎣x⎦|!) + _{22+735235|⎣x⎦|}C₂₃₅₆ + φ(|⎣x⎦|+1) + 72x⁴ + 4x³ - 11x² - 6x + 13의 그래프가 교차하는 가장 큰 x 값을 찾으세요. 여기서 ⎣x⎦는 x의 바닥 함수이고, φ(n)은 n 이하의 양의 정수 중 n과 서로소인 수의 합을 나타냅니다.

풀이) 함수의 복잡한 부분은 무시할 수 있습니다. 교차 여부를 결정하는 것은 f(x)-g(x)=0인지 여부입니다. g(x) - f(x) = x³ - 5x² - 8x + 12 = (x-6)(x+2)(x-1)이므로, 그래프가 교차하는 가장 큰 x 값은 x=6입니다.

답) 6

190

문제) 다섯 점 A, B, C, D, O가 평평한 필드에 놓여 있습니다. A는 O의 바로 북쪽에 있고, B는 O의 바로 서쪽에 있으며, C는 O의 바로 남쪽에 있고, D는 O의 바로 동쪽에 있습니다. C와 D 사이의 거리는 140m입니다. 열기구가 O의 바로 위 공중에 H에 위치해 있습니다. 열기구는 네 개의 밧줄 HA, HB, HC, HD로 고정되어 있습니다. 밧줄 HC의 길이는 150m이고 밧줄 HD의 길이는 130m입니다. 아래는 도형을 그리는 코드입니다.

size(250);
pair A, B, C, D, O, H, W, X, Y, Z;
O=(0,0);
A=(1,1);
D=(1.5,-.3);
B=(-1.5,.3);
C=(-1,-1);
H=(0,2.5);
W=(5/3)*(A+D);
X=(5/3)*(A+B);
Y=(-1)*(W);
Z=(-1)*(X);
draw(W--X--Y--Z--W);
draw(A--C);
draw(B--D);
draw(O--H, linewidth(1));
draw(A--H, dashed);
draw(B--H, dashed);
draw(C--H, dashed);
draw(D--H, dashed);
dot(A);
dot(B);
dot(C);
dot(D);
dot(O);
dot(H);
label("A", A, NE);
label("B", B, SW);
label("C", C, SE);
label("D", D, NE);
label("O", O, SE);
label("H", H, NW);

풀이) 가장 많은 밧줄을 절약하려면 HP의 길이가 최소가 되어야 합니다. HP가 최소가 되려면 HP는 CD에 수직이어야 합니다.

pair C, D, H, P;
H=(90,120);
C=(0,0);
D=(140,0);
P=(90,0);
draw(H--C--D--H--P);
label("H", H, N);
label("C", C, SW);
label("D", D, SE);
label("P", P, S);
label("150", (C+H)/2, NW);
label("130", (D+H)/2, NE);

(이 도형에서 P를 수직 위치에서 멀리 이동시키면 HP가 길어지는 것을 볼 수 있습니다.) 도형에서 HC=150, HD=130, CD=140입니다. HP를 x, PD를 a라고 합시다. 그러면 CP=140-a입니다. 피타고라스 정리에 의해 △HPC에서 x² + (140-a)² = 150²입니다. △HPD에서 x² + a² = 130²입니다. 첫 번째 식에서 두 번째 식을 빼면, (140-a)² - a² = 150² - 130² (19600 - 280a + a²) - a² = 5600 19600 - 280a = 5600 280a = 14000 a = 50 따라서 x² + 90² = 150² 또는 x² = 150² - 90² = 22500 - 8100 = 14400이므로 x = 120입니다. 따라서 사용할 수 있는 가장 짧은 밧줄은 120m이며, 이는 130 + 150 - 120 = 160 m의 밧줄을 절약합니다.

답) 160

191

문제) Paul과 Jesse는 각각 처음 여섯 개의 소수 중에서 무작위로 숫자를 선택합니다. 그들이 선택한 숫자의 합이 짝수가 될 확률은 얼마입니까?

풀이) Paul과 Jesse가 선택한 숫자의 합이 홀수가 되는 유일한 방법은 둘 중 하나가 2를 선택하고 다른 하나가 홀수 소수를 선택하는 경우입니다. Paul이 2를 선택하고 Jesse가 홀수 소수를 선택하는 경우는 5가지가 있으며, Jesse가 2를 선택하고 Paul이 홀수 소수를 선택하는 경우도 5가지가 있습니다. Paul과 Jesse가 숫자를 선택하는 총 가능한 경우의 수는 6 × 6 = 36이므로, Paul과 Jesse가 선택한 숫자의 합이 짝수가 아닌 확률은 10 / 36 = 5 / 18입니다. 따라서, Paul과 Jesse가 선택한 숫자의 합이 짝수일 확률은 1 - 5 / 18 = 13 / 18입니다.

답) 13 / 18

192

문제) 점 (a, b)가 직선 3x + 2y = 12 위에 있습니다. a = 4일 때, b의 값은 얼마입니까?

풀이) x = 4를 대입합니다: 3(4) + 2y = 12 12 + 2y = 12 y = 0. 따라서, b = 0입니다.

답) 0

193

문제) 삼각형 PQR에서, PQ = QR = 34이고 PR = 32입니다. 중선 QM의 길이를 구하세요.

풀이) 삼각형 PQR은 이등변삼각형으로 PQ = QR이므로, 중선 QM은 또한 높이입니다. 아래는 도형을 그리는 코드입니다.

size(100);
pair P,Q,R,M,NN;
P = (0,0);
Q = (0.5,0.9);
R = (1,0);
NN = (0.5,0);
M = (Q+R)/2;
draw(rightanglemark(Q,NN,P,2.5));
draw(P--Q--R--P);
draw(Q--NN);
label("$P$",P,SW);
label("$R$",R,SE);
label("$Q$",Q,N);
label("$M$",NN,S);

MP = PR / 2 = 16이므로, 직각삼각형 PQM에서 QM = √(PQ² - PM²) = √(34² - 16²) = √((34 - 16)(34 + 16)) = 30. (또한 PM / PQ = 8 / 17이므로, QM / PQ = 15 / 17임을 인식할 수도 있습니다.)

답) 30

194

문제) 정수 계수를 가진 다항식은 다음과 같은 형태입니다. 2x⁴ + a₃x³ + a₂x² + a₁x + 1 = 0. 이 다항식의 서로 다른 유리근의 개수를 구하세요.

풀이) 유리근 정리에 따르면, 가능한 유리근은 ±a/b의 형태이며, 여기서 a는 1의 약수이고 b는 2의 약수입니다. 따라서 가능한 유리근은 다음과 같습니다. ±1, ±1/2. 따라서 가능한 유리근의 개수는 4개입니다.

답) 4

195

문제) 모든 실수 x와 y에 대해 x - y / x⁴ + y⁴ + 6의 최대값을 구하세요.

풀이) 명백히, 최대값은 x가 양수이고 y가 음수일 때 발생합니다. z = -y라고 하면, z는 양수이고 y = -z입니다. 그러면 x - y / x⁴ + y⁴ + 6 = x + z / x⁴ + z⁴ + 6입니다. AM-GM 부등식에 의해, x⁴ + 1 + 1 + 1 ≥ 4 ⁴√(x⁴) = 4x, 그리고 z⁴ + 1 + 1 + 1 ≥ 4 ⁴√(z⁴) = 4z입니다. 따라서 x⁴ + z⁴ + 6 ≥ 4(x + z)이고, 이는 x + z / x⁴ + z⁴ + 6 ≤ 1 / 4를 의미합니다. 평등은 x = z = 1일 때 발생하므로, 최대값은 1/4입니다.

답) 1/4

196

문제) 4차 단항식 p(x)가 있다고 하자. p(x)의 세 근은 1, 2, 3이다. p(0) + p(4)의 값을 구하시오.

풀이) 세 근이 1, 2, 3이므로, 다음과 같이 쓸 수 있습니다. p(x) = (x - 1)(x - 2)(x - 3)(x - r) 그러면 p(0) + p(4) = (-1)(-2)(-3)(-r) + (3)(2)(1)(4 - r) = 6r + 24 - 6r = 24.

답) 24

197

문제) 441 + 2(21)(19) + 361 = x. x를 구하세요.

풀이) 361은 19²이고 441은 21²이므로, x = 21² + 2(21)(19) + 19²입니다. 이는 이항식 전개로 (21 + 19)² = 40² = 1600입니다.

답) 1600

198

문제) 만약 x³이 10!의 양의 인수라면, 가능한 x의 정수 값은 몇 개입니까? (참고: 양의 정수 n에 대해, 표현식 n!은 1부터 n까지의 정수의 곱을 나타냅니다.)

풀이) 먼저 10!을 소인수분해합니다: 10! = 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 2⁸ · 3⁴ · 5² · 7. 따라서 x는 1, 2¹, 2², 3, 2¹ · 3, 또는 2² · 3이 될 수 있으며, 가능한 x의 값은 총 6개입니다.

답) 6

199

문제) 6명의 여자와 2명의 남자가 한 줄로 앉을 때, 2명의 남자가 반드시 서로 옆에 앉아야 한다면 몇 가지 방법이 있을까요?

풀이) 2명의 남자를 한 사람으로 간주하고, 먼저 '7명'을 배열한 다음, 2명의 남자를 배열할 수 있습니다. 따라서 남자들이 함께 앉는 배열의 수는 7! × 2! = 10,080입니다.

답) 10,080

200

문제) 7, 2, x, 10의 산술 평균이 9입니다. x의 값은 얼마입니까?

풀이) 이 4개의 숫자의 평균이 9라면, 이들의 합은 4 × 9 = 36이어야 합니다. 그러면, 36에서 나머지 세 숫자를 빼면 됩니다: 36 - 7 - 2 - 10 = 17 = x.

답) 17

201

문제) 4 daps = 7 yaps이고, 5 yaps = 3 baps일 때, 42 baps는 몇 daps와 같습니까?

풀이) 5 yaps = 3 baps를 14로 곱하면 70 yaps가 42 baps와 같다는 것을 알 수 있습니다. 그런 다음 4 daps = 7 yaps를 10으로 곱하면 70 yaps가 40 daps와 같다는 것을 알 수 있습니다.

답) 40

202

문제) 학생 수가 N명인 그룹이 있으며, N < 50입니다. 선생님이 학생들을 8명씩 그룹으로 나누면 마지막 그룹에는 5명이 남습니다. 만약 선생님이 학생들을 6명씩 그룹으로 나누면 마지막 그룹에는 3명이 남습니다. 가능한 모든 N의 값을 더한 값은 얼마입니까?

풀이) N ≡ 5 (mod 8)이고 N ≡ 3 (mod 6)임이 주어졌습니다. 8의 배수에 5를 더한 수를 확인해보면, 5와 13은 6의 배수에 3을 더한 수가 아니지만, 21은 6의 배수에 3을 더한 수입니다. 따라서 21은 가능한 N의 값 중 하나입니다. 중국인의 나머지 정리에 따르면, x ≡ 5 (mod 8)이고 x ≡ 3 (mod 6)을 만족하는 정수 x는 x = 21 + lcm(6, 8)k = 21 + 24k 형태입니다. 여기서 k는 정수입니다. 따라서 50보다 작은 두 해는 21과 21 + 24(1) = 45이며, 이들의 합은 21 + 45 = 66입니다.

답) 66

203

문제) 앨리스와 밥이 게임을 하고 있습니다. 앨리스가 먼저 시작합니다. 앨리스의 차례에, 그녀는 동전을 던집니다. 앞면이 나오면 그녀가 승리합니다. 그렇지 않으면 밥의 차례가 됩니다. 밥의 차례에, 그는 동전을 던집니다. 뒷면이 나오면 그가 승리합니다. 그렇지 않으면 앨리스의 차례가 됩니다. 앨리스가 게임에서 이길 확률은 얼마입니까?

풀이) 앨리스가 첫 번째 차례에 게임에서 이길 확률은 1/2입니다. 그녀가 이기지 못하면, 두 번째 차례에 게임에서 이길 확률은 1/8입니다. 이는 첫 번째 던지기에서 이기지 못할 확률 (1/2), 밥이 첫 번째 던지기에서 이기지 못할 확률 (1/2), 그리고 앨리스가 두 번째 던지기에서 이길 확률 (1/2)을 곱한 것입니다. 그녀가 세 번째 차례에 게임에서 이길 확률은 1/32이며, 일반적으로 그녀가 k번째 차례에 게임에서 이길 확률은 (1/2)²ᵏ⁻¹입니다. 따라서, 앨리스가 이길 확률은 첫 번째 항이 1/2이고 공비가 1/4인 무한 등비급수입니다. 따라서, 앨리스가 게임에서 이길 확률은 1/2 / (1 - 1/4) = 2/3입니다. 또는 앨리스와 밥의 승리 확률의 유일한 차이는 누가 먼저 시작하느냐입니다. 밥이 두 번째로 시작하기 때문에, 그가 k번째 던지기에서 이길 확률은 앨리스가 k번째 던지기에서 이길 확률의 절반입니다. 이는 앨리스가 먼저 뒷면을 얻어야 밥이 이길 기회를 얻기 때문입니다. 따라서, a가 앨리스의 승리 확률이고, b가 밥의 승리 확률이라면, a = 2b입니다. 또한, 누군가는 반드시 이겨야 하므로, a + b = 1입니다. 따라서 a = 2/3이고 b = 1/3이므로, 앨리스가 게임에서 이길 확률은 2/3입니다.

답) 2/3

204

문제) (5x + 9)⁶¹¹ + (x + 5)¹¹ + (x - 1)¹¹ + 3x² + 1을 x + 2로 나눌 때의 나머지를 구하세요.

풀이) 나머지 정리에 따라 나머지를 찾기 위해 x = -2를 대입합니다. 이렇게 하면 다음과 같습니다. (-1)⁶¹¹ + 3¹¹ + (-3)¹¹ + 3(-2)² + 1 = 12

답) 12

205

문제) 서로 다른 복소수 a, b, c, d가 |a| = |b| = |c| = |d| = 1이고 a + b + c + d = 0를 만족한다고 하자. 다음 식의 최대값을 구하시오: |(a + b)(a + c)(a + d)(b + c)(b + d)(c + d)|.

풀이) 복소수 a에 대해 |a| = 1이므로, aā = |a|²이고, 따라서 ā = 1 / a입니다. 마찬가지로, b̅ = 1 / b, c̄ = 1 / c, d̅ = 1 / d입니다. 식 a + b + c + d = 0에서 ā + b̅ + c̄ + d̅ = 0이므로, 1/a + 1/b + 1/c + 1/d = 0. 이를 통해 abc + abd + acd + bcd = 0을 얻습니다. 비에타의 정리에 따르면, a, b, c, d는 다음과 같은 다항식의 근입니다: z⁴ + p₂ z² + p_0 = 0. 만약 z가 이 다항식의 근이라면, -z도 근입니다. 이는 -a가 b, c, d 중 하나와 같다는 것을 의미하므로, (a + b)(a + c)(a + d)(b + c)(b + d)(c + d) = 0. 따라서 최대값은 0입니다.

답) 0

206

문제) 행렬 A 가 다음과 같다고 하자: A (3, 1, 0) = (2, 4, -3) 그리고 A (-5, 2, 2) = (0, -5, -5). A (-13, 3, 4) 를 구하시오.

풀이) 방정식 A (3, 1, 0) = (2, 4, -3) 과 A (-5, 2, 2) = (0, -5, -5) 을 빼면, A (-8, 1, 2) = (-2, -9, -2) 을 얻습니다. 그런 다음, 방정식 A (-5, 2, 2) = (0, -5, -5) 과 A (-8, 1, 2) = (-2, -9, -2) 을 더하면, A (-13, 3, 4) = (-2, -14, -7) 을 얻습니다.

답) (-2, -14, -7)

207

문제) 한 직선이 다음과 같이 매개변수화되어 있습니다. (x, y) = (8, -1) + t (2, 3). 이 직선의 방정식은 형태 y = mx + b 로 표현될 수 있습니다. 순서쌍 (m, b)를 입력하세요.

풀이) 우리는 x = 8 + 2t 와 y = -1 + 3t 를 가지고 있습니다. x = 8 + 2t 에서 t 를 고립시키면, t = (x - 8) / 2 입니다. 그러면 y = -1 + 3t = -1 + 3 · (x - 8) / 2 = 3/2 x - 13 따라서, (m, b) = (3/2, -13)입니다.

답) (3/2, -13)

208

문제) Mikka는 두 가지 다른 토핑으로 피자를 주문하고 싶어합니다. 그는 선택할 수 있는 8가지 다른 토핑이 있습니다. 그는 몇 가지 다른 피자를 주문할 수 있을까요?

풀이) 8가지 토핑이 있으며, 우리는 2개의 서로 다른 토핑을 선택해야 합니다. 이는 8개의 요소로 이루어진 집합에서 2개의 요소로 이루어진 부분집합의 수로 표현됩니다. 이 수는 이항 계수 8C2 = 28로 계산됩니다.

답) 28

209

문제) 처음 100개의 양의 정수 중에서 3, 4, 5로 나누어 떨어지는 수는 몇 개입니까?

풀이) 우리는 나눗셈 규칙을 사용하여 이 문제를 해결할 수 있지만, 이는 꽤 번거로울 것입니다. 3, 4, 5로 나누어 떨어지는 수는 이들의 곱인 3 × 4 × 5 = 60으로 나누어 떨어져야 한다는 점을 주목하는 것이 더 쉽습니다. 이는 여러 정수로 나누어 떨어지는 수는 그들의 최소 공배수로 나누어 떨어져야 하기 때문입니다. 그러나 3, 4, 5는 서로소이므로 최소 공배수는 단순히 세 수의 곱입니다. 분명히, 1과 100 사이에서 60으로 나누어 떨어지는 수는 단 하나, 즉 60입니다. 따라서 그러한 수는 단 하나, 1개입니다.

답) 1

210

문제) 두 자리 정수 "AB"를 세제곱했을 때, 그 값이 912,673입니다. A + B는 얼마입니까?

풀이) 90³ = 729,000이므로, AB는 90보다 큽니다. 따라서 A = 9입니다. AB³의 일의 자리가 3이므로, AB는 홀수여야 합니다. AB³의 일의 자리는 B³의 일의 자리와 같으므로, 홀수의 세제곱의 일의 자리를 살펴봅니다. 1³의 일의 자리는 1입니다. 3³의 일의 자리는 7입니다. 5³의 일의 자리는 5입니다. 7³의 일의 자리는 3입니다. 9³의 일의 자리는 9입니다. 7³만이 일의 자리가 3이므로, B = 7입니다. 따라서 A + B = 9 + 7 = 16입니다.

답) 16

211

문제) 열두 개의 1×1 정사각형이 직사각형을 형성합니다. 아래는 도형을 그리는 코드입니다.

size(4cm);defaultpen(linewidth(0.75));

// Filled portions
fill((0, 4)--(0, 0)--(2, 0)--cycle, gray(0.75));
fill((0, 4)--(3, 4)--(3, 0)--cycle, gray(0.75));

// grid
int j;
for (j = 0; j < 4; ++j) {draw((j, 0)--(j, 4));}
for (j = 0; j < 5; ++j) {draw((0, j)--(3, j));}

//diagonals
draw((0, 4)--(3, 0)); draw((0, 4)--(2, 0));

이때, 음영 처리된 부분의 총 면적은 얼마입니까?

풀이) 직사각형의 총 면적은 3 × 4 = 12입니다. 음영 처리된 부분의 총 면적은 직사각형의 총 면적(12)에서 음영이 없는 부분의 면적을 뺀 값과 같습니다. 음영이 없는 부분은 밑변의 길이가 1이고 높이가 4인 삼각형입니다. 이 부분의 면적은 1/2 × 1 × 4 = 2입니다. 따라서, 음영 처리된 부분의 총 면적은 12 - 2 = 10입니다.

답) 10

212

문제) 다음을 정수로 표현하세요: 5⁵ ÷ 5⁴ - 5³ + 5² · 5¹

풀이) 양의 정수 m > n에 대해 aᵐ ÷ aⁿ = aᵐ⁻ⁿ이고, aᵐ · aⁿ = aᵐ⁺ⁿ임을 기억하세요. 이제 5⁵ ÷ 5⁴ - 5³ + 5² · 5¹을 5¹ - 5³ + 5³로 쓸 수 있습니다. 뺄셈의 정의와 덧셈의 결합법칙을 사용하면 다음과 같습니다: 5¹ - 5³ + 5³ = 5¹ + (-5³ + 5³) = 5¹ + 0 = 5.

답) 5

213

문제) 최근에 프랭크는 100문제의 적성 검사를 치렀습니다. 각 정답은 5점, 각 오답은 -2점, 답하지 않은 문제는 0점이었습니다. 프랭크는 80문제를 답했고, 총 232점을 받았습니다. 프랭크가 맞힌 문제는 몇 문제입니까?

풀이) 프랭크가 맞힌 문제의 수를 a, 틀린 문제의 수를 b라고 합시다. 다음 두 방정식을 세울 수 있습니다. a + b = 80 5a - 2b = 232 첫 번째 방정식에서 b = 80 - a입니다. 이를 두 번째 방정식에 대입하여 b를 제거하면, 5a - 2(80 - a) = 232 a = 56 따라서, 프랭크는 56문제를 맞혔습니다.

답) 56

214

문제) 다음 급수를 계산하세요: ∑_{n=1 to ∞} (Fₙ₊₁ / (Fₙ Fₙ₊₂)), 여기서 Fₙ은 n번째 피보나치 수를 나타내며, F₀ = 0이고 F₁ = 1입니다.

풀이) Fₙ₊₁ = Fₙ₊₂ - Fₙ이므로, (Fₙ₊₁ / (Fₙ Fₙ₊₂)) = (1 / Fₙ) - (1 / Fₙ₊₂). 따라서, ∑_{n=1 to ∞} (1 / (Fₙ Fₙ₊₂)) = (1 / F₁) - (1 / F₃) + (1 / F₂) - (1 / F₄) + (1 / F₃) - (1 / F₅) + ... = 1 / F₁ + 1 / F₂ = 2.

답) 2

215

문제) 우리 학교에는 360명의 학생이 있습니다. 15명은 미적분학, 물리학, 화학을 모두 듣고, 15명은 아무 과목도 듣지 않습니다. 180명은 미적분학을 듣습니다. 화학을 듣는 학생 수는 물리학을 듣는 학생 수의 두 배입니다. 75명은 미적분학과 화학을 모두 듣고, 75명은 물리학과 화학을 모두 듣습니다. 오직 30명만이 물리학과 미적분학을 모두 듣습니다. 물리학을 듣는 학생은 몇 명입니까?

풀이) 물리학을 듣는 학생 수를 x라고 하면, 화학을 듣는 학생 수는 2x입니다. 세 과목을 모두 듣는 학생은 15명이고, 물리학과 미적분학을 모두 듣는 학생은 30명이므로, 오직 물리학과 미적분학을 듣는 학생은 30 - 15 = 15명입니다. 마찬가지로, 오직 화학과 미적분학을 듣는 학생은 60명이고, 물리학과 화학을 듣는 학생은 60명입니다. 물리학을 듣는 학생이 x명이고, 다른 과목과 함께 물리학을 듣는 학생이 15 + 15 + 60 = 90명이므로, 오직 물리학만 듣는 학생은 x - 90명입니다. 마찬가지로, 오직 화학만 듣는 학생은 2x - 135명이고, 오직 미적분학만 듣는 학생은 90명입니다. 아무 과목도 듣지 않는 학생이 15명이라는 것을 알 때, 이 여덟 가지 범주의 학생 수의 합은 학교의 총 학생 수인 360명입니다: (x - 90) + (2x - 135) + 90 + 60 + 15 + 60 + 15 + 15 = 360. 이를 풀어보면, 물리학을 듣는 학생 수는 x = 110명입니다.

답) 110

216

문제) 만약 x² - x - 1 = 0이라면, x³ - 2x + 1의 값은 얼마입니까?

풀이) x² - x - 1 = 0을 재배열하면 x² = x + 1이 됩니다. 따라서 x² 대신 x + 1을 반복적으로 대입하면 다음과 같습니다. x³ - 2x + 1 = x(x²) - 2x + 1 = x(x + 1) - 2x + 1 = x² + x - 2x + 1 = x² - x + 1 = (x + 1) - x + 1 = 2

답) 2

217

문제) 잉크의 땅에서는 독특한 화폐 시스템이 있습니다. 1 트링킷은 4 블링킷과 같고, 3 블링킷은 7 드링킷과 같습니다. 56 드링킷의 가치는 몇 트링킷입니까?

풀이) 3 블링킷 = 7 드링킷을 8로 곱하여 24 블링킷이 56 드링킷과 같다는 것을 찾습니다. 1 트링킷 = 4 블링킷을 6으로 곱하여 6 트링킷이 24 블링킷과 같다는 것을 찾습니다 (이는 우리가 방금 찾은 56 드링킷과 같습니다).

답) 6

218

문제) 모든 자릿수가 0과 1로만 이루어진 450의 가장 작은 양의 배수는 무엇입니까?

풀이) 어떤 수가 450으로 나누어지려면, 450의 모든 약수, 즉 9와 50으로도 나누어져야 합니다. 어떤 수가 9로 나누어지려면, 그 수의 자릿수의 합이 9로 나누어져야 합니다. 양의 정수는 적어도 하나의 0이 아닌 자릿수를 가져야 하므로, 우리가 찾고 있는 수는 적어도 9개의 1을 자릿수로 가져야 합니다. 또한, 우리가 찾고 있는 수는 50으로 나누어져야 하므로, 50 또는 00으로 끝나야 합니다. 숫자 5는 허용되지 않으므로, 우리의 수는 00으로 끝나야 하며, 따라서 가장 작은 후보는 11,111,111,100입니다. 실제로 9와 50이 이 수를 나누기 때문에, 그리고 450이 9와 50의 최소공배수이기 때문에, 450은 11,111,111,100을 나눌 수 있습니다. 따라서 이 수가 정답입니다.

답) 11,111,111,100

219

문제) 점 (-5, 5)와 (3, 7)을 잇는 선분의 중점을 구하세요. 답을 순서쌍 (x, y) 형태로 표현하세요.

풀이) 중점 공식을 적용하면 다음과 같습니다: ((-5 + 3) / 2, (5 + 7) / 2) = (-1, 6).

답) (-1, 6)

220

문제) 보여지는 바퀴가 두 번 회전하여, 포인터가 가리키는 숫자가 무작위로 결정됩니다 (바퀴의 각 숫자가 동일한 확률로 선택됨). 이렇게 결정된 두 숫자가 기록됩니다. 첫 번째 숫자는 4로 나누어져, 체커보드의 열을 나타내는 나머지 1, 2, 3 중 하나를 결정합니다. 두 번째 숫자는 5로 나누어져, 체커보드의 행을 나타내는 나머지 1, 2, 3, 4 중 하나를 결정합니다. 마지막으로, 이 열과 행이 만나는 칸에 체커가 놓입니다. 체커가 체커보드의 음영 칸에 놓일 확률은 얼마입니까? 아래는 도형을 그리는 코드입니다.

unitsize(1cm);
draw(Circle((0,0),2),linewidth(0.7));
draw((1.7,1)--(-1.7,-1),linewidth(0.7));
draw((1.7,-1)--(-1.7,1),linewidth(0.7));
draw((0,2)--(0,-2));
label("1",(0.8,0.5),NW);
label("2",(0.8,-0.5),SW);
label("6",(-0.8,0.5),NE);
label("9",(-0.8,-0.5),SE);
label("3",(-0.7,0),W);
label("7",(0.7,0),E);
draw((-2.8,0)--(-2.1,0),Arrow);
label("Pointer",(-2.8,0),W);
fill((3,0)--(3,1)--(4,1)--(4,0)--cycle,gray(0.7));
fill((3,-2)--(3,-1)--(4,-1)--(4,-2)--cycle,gray(0.7));
fill((4,1)--(4,2)--(5,2)--(5,1)--cycle,gray(0.7));
fill((4,-1)--(4,0)--(5,0)--(5,-1)--cycle,gray(0.7));
fill((5,0)--(5,1)--(6,1)--(6,0)--cycle,gray(0.7));
fill((5,-2)--(5,-1)--(6,-1)--(6,-2)--cycle,gray(0.7));
draw((3,-2)--(3,2)--(6,2)--(6,-2)--cycle,linewidth(0.7));
draw((3,-1)--(6,-1),linewidth(0.7));
draw((3,0)--(6,0),linewidth(0.7));
draw((3,1)--(6,1),linewidth(0.7));
draw((4,-2)--(4,2),linewidth(0.7));
draw((5,-2)--(5,2),linewidth(0.7));
label("1",(3.5,-2),S);
label("2",(4.5,-2),S);
label("3",(5.5,-2),S);
label("1",(3,-1.5),W);
label("2",(3,-0.5),W);
label("3",(3,0.5),W);
label("4",(3,1.5),W);

풀이) 첫 번째 나머지가 짝수일 확률은 2/6 = 1/3이고, 홀수일 확률은 2/3입니다. 두 번째 나머지가 짝수일 확률은 3/6 = 1/2이고, 홀수일 확률은 1/2입니다. 첫 번째 나머지의 홀짝성과 두 번째 나머지의 홀짝성은 서로 독립적입니다. 왜냐하면 이들은 바퀴의 별도 회전에 의해 결정되기 때문입니다. 음영 칸은 두 나머지가 모두 홀수이거나 모두 짝수일 때입니다. 따라서 칸이 음영일 확률은 다음과 같습니다: (1/3) · (1/2) + (2/3) · (1/2) = 1/2.

답) 1/2

221

문제) Sam은 헛간에서 집까지 2갤런의 우유가 든 양동이를 나르고 있습니다. 집까지의 거리는 3마일입니다. 그러나 양동이에 구멍이 나 있습니다. Sam이 1마일을 걸을 때마다 양동이에는 처음 마일 시작 시의 우유의 2 / 3 만큼이 남습니다. Sam이 집에 도착했을 때 양동이에는 몇 갤런의 우유가 남아 있을까요?

풀이) 첫 번째 마일이 끝날 때, 양동이에는 처음 우유의 2 / 3 만큼이 남아 있을 것입니다. 추가적인 마일마다 이 양은 2 / 3 만큼 곱해집니다. 따라서 세 번째 마일이 끝나고 집에 도착했을 때, 양동이에는 2 / 3 · 2 / 3 · 2 / 3 = (2 / 3)³ 만큼의 우유가 남아 있을 것입니다. 처음에 2갤런이 있었으므로, 집에 도착했을 때 양동이에 남아 있는 양은 2 · (2 / 3)³ 입니다. (a / b)ⁿ = (aⁿ) / (bⁿ) 이므로, 이 표현은 2 · (2³) / (3³) 와 같습니다. nᵃ · nᵇ = nᵃ⁺ᵇ 이므로, 이는 (2⁴) / (3³) 와 같습니다. 지수를 계산하면, 16 / 27 갤런이 됩니다.

답) 16 / 27

222

문제) 정수 240과 k의 곱이 완전 세제곱입니다. 가능한 가장 작은 양수 k의 값은 무엇입니까?

풀이) 240 = 2⁴·3·5 = 2³(2·3·5). 240k가 완전 세제곱이 되기 위해서는, k는 최소한 2²·3²·5² = 900이어야 합니다.

답) 900

223

문제) 삼각형 ABC의 넓이는 6 제곱 센티미터입니다. 선분 AB는 선분 DE와 평행합니다. BD = 4BC입니다. 삼각형 CDE의 넓이는 몇 제곱 센티미터입니까? 아래는 도형을 그리는 코드입니다.

draw((-.3,-3)--(.1,1)--(-1,0)--(3,0)--cycle);
label("$A$",(.1,1),N);
label("$B$",(-1,0),W);
label("$C$",(0,0),NE);
label("$D$",(3,0),E);
label("$E$",(-.3,-3),S);

풀이) AB ∥ DE이므로, ∠A = ∠E이고 ∠B = ∠D입니다. 따라서 삼각형 ABC는 삼각형 EDC와 닮음입니다. BD = 4BC이므로, CD = BD - BC = 3BC입니다. 따라서 삼각형 ABC와 EDC의 변의 비율은 1:3이고, 넓이의 비율은 1:9입니다. 삼각형 ABC의 넓이가 6 cm²이므로, 삼각형 CDE의 넓이는 54 cm²입니다.

답) 54

224

문제) 분수 4321 / (5⁷ · 2⁸)의 유한 소수 표현에서 각 자리 숫자의 합은 얼마입니까?

풀이) 4321 / (5⁷ · 2⁸)을 분모가 10⁸인 소수로 다시 쓰면, (4321 / (5⁷ · 2⁸)) · (5¹ / 5¹) = (4321 · 5) / 10⁸ = 21605 / 10⁸ = 0.00021605 따라서, 소수 표현의 각 자리 숫자의 합은 2 + 1 + 6 + 0 + 5 = 14입니다.

답) 14

225

문제) 다음을 구하세요: sin 20° sin 40° sin 60° sin 80° sin 100° sin 120° sin 140° sin 160°.

풀이) 먼저, sin 60° = sin 120° = √3 / 2 이므로, sin 20° sin 40° sin 60° sin 80° sin 100° sin 120° sin 140° sin 160° = 3/4 sin 20° sin 40° sin 80° sin 100° sin 140° sin 160°. 여기서 sin 80° = sin 100° = cos 10°, sin 140° = sin 40°, sin 160° = sin 20° 이므로, 3/4 sin 20° sin 40° sin 80° sin 100° sin 140° sin 160° = 3/4 cos² 10° sin² 20° sin² 40° = 3/4 (cos 10° sin 20° sin 40°)². 곱을 합으로 변환하면, cos 10° sin 20° sin 40° = cos 10° · 1/2 (cos 20° - cos 60°) = 1/2 cos 10° (cos 20° - 1/2) = 1/2 cos 10° cos 20° - 1/4 cos 10° = 1/4 (cos 30° + cos 10°) - 1/4 cos 10° = 1/4 cos 30° = √3 / 8. 따라서, 이 표현은 3/4 (√3 / 8)² = 9/256 입니다.

답) 9/256

226

문제) 다음 식의 값을 구하세요: (3x-2)(4x+1)-(3x-2)4x+1 여기서 x=4입니다.

풀이) 다음을 계산합니다: (3x-2)(4x+1)-(3x-2)4x+1 =(3x-2)(4x+1-4x)+1 =(3x-2) · 1 + 1 = 3x-1 여기서 x=4일 때, 값은 3 · 4 - 1 = 11입니다.

답) 11

227

문제) 구별할 수 없는 5개의 공을 구별할 수 없는 2개의 상자에 넣는 방법은 몇 가지입니까?

풀이) 공과 상자가 모두 구별할 수 없으므로, 한 상자에 5개, 다른 상자에 0개를 넣는 경우, 한 상자에 4개, 다른 상자에 1개를 넣는 경우, 또는 한 상자에 3개, 다른 상자에 2개를 넣는 경우가 있습니다. 따라서 총 3가지의 다른 배열이 가능합니다.

답) 3

228

문제) 상수 c에 대해, 원통 좌표 (r, θ, z)에서 다음 방정식으로 설명되는 형태를 찾으세요. z = c. (A) 직선 (B) 원 (C) 평면 (D) 구 (E) 원기둥 (F) 원뿔 정답의 문자를 입력하세요.

풀이) 원통 좌표에서 z는 단순히 점의 z-좌표를 나타냅니다. 따라서 고정된 z-좌표 c에 대해, 모든 점은 xy-평면에 평행한 평면 위에 놓입니다. 정답은 (C)입니다. 아래는 도형을 그리는 코드입니다.

import three;
import solids;

size(200);
currentprojection = perspective(6,3,2);
currentlight = (1,0,1);
real theta = 120;

draw((-2,0,0)--(2,0,0));
draw((0,-2,0)--(0,2,0));
draw(surface((1,1,0.5)--(1,-1,0.5)--(-1,-1,0.5)--(-1,1,0.5)--cycle),gray(0.99));
draw((0,0,-2)--(0,0,0.2));
draw((0,0,0.5)--(0,0,2));

label("$x$", (2,0,0), SW);
label("$y$", (0,2,0), E);
label("$z$", (0,0,2), N);
label("$z = c$", (-1,1,0.5), E);

답) (C)

229

문제) 점 P에 대해, d₁, d₂, d₃는 각각 P에서 평면 x - z = 0, x - 2y + z = 0, x + y + z = 0까지의 거리를 나타냅니다. 집합 S는 다음 조건을 만족하는 점 P의 집합입니다. d₁² + d₂² + d₃² = 36. S에 의해 둘러싸인 부피의 영역을 찾으세요.

풀이) P = (a, b, c)라고 하겠습니다. 그러면 P에서 평면 x - z = 0까지의 거리는 d₁ = |a - c| / √2. P에서 평면 x - 2y + z = 0까지의 거리는 d₂ = |a - 2b + c| / √6. 그리고 P에서 평면 x + y + z = 0까지의 거리는 d₃ = |a + b + c| / √3. 그러면 식 d₁² + d₂² + d₃² = 36은 다음과 같이 됩니다. (a - c)² / 2 + (a - 2b + c)² / 6 + (a + b + c)² / 3 = 36. 이를 정리하면 a² + b² + c² = 36이 됩니다. 따라서 S는 반지름이 6인 구이고, 그 부피는 (4 / 3) π · 6³ = 288π입니다.

답) 288π

230

문제) Yann과 Camille은 식당에 갑니다. 메뉴에 10개의 요리가 있을 때, 각자 하나의 요리를 주문한다고 할 때, Yann과 Camille이 같은 요리를 주문하지 않는 경우, 몇 가지 다른 조합의 식사를 주문할 수 있을까요? (Yann이 치킨을 주문하고 Camille이 생선을 주문하는 것과 Yann이 생선을 주문하고 Camille이 치킨을 주문하는 것은 다릅니다.)

풀이) Yann은 10개의 다른 요리를 주문할 수 있습니다. Yann이 요리를 선택한 후, Camille은 Yann이 선택한 요리를 제외한 9개의 선택지가 남습니다. 따라서 총 10 · 9 = 90가지의 다른 식사 조합이 가능합니다.

답) 90

231

문제) 실수 a, b, c, d, e가 다음 조건을 만족한다고 하자: a + b + c + d + e = 8, a² + b² + c² + d² + e² = 16. e의 최대값을 구하시오.

풀이) 코시-슈바르츠 부등식에 의해, (a² + b² + c² + d²)(1 + 1 + 1 + 1) ≥ (a + b + c + d)². 따라서, (16 - e²)(4) ≥ (8 - e)². 이를 정리하면 16e - 5e² ≥ 0, 또는 e(16 - 5e) ≥ 0. 따라서, e ≤ 16 / 5. 등호는 a = b = c = d = 6 / 5이고 e = 16 / 5일 때 성립하므로, e의 최대값은 16 / 5이다.

답) 16 / 5

232

문제) Amy, Ben, Chris의 나이 평균이 6입니다. 4년 전, Chris의 나이는 현재 Amy의 나이와 같았습니다. 4년 후, Ben의 나이는 그때의 Amy 나이의 3/5가 될 것입니다. Chris는 현재 몇 살입니까?

풀이) Amy, Ben, Chris의 나이를 각각 a, b, c라고 합시다. 다음과 같은 방정식을 세울 수 있습니다. (1) (a + b + c) / 3 = 6 → a + b + c = 18 (2) c - 4 = a (3) b + 4 = 3/5 × (a + 4) 방정식 (3)에서, b = 3/5 × (a + 4) - 4가 됩니다. 방정식 (2)를 방정식 (3)에 대입하여 a를 제거하면, b = 3/5 × c - 4가 됩니다. 이 마지막 방정식과 방정식 (2)를 방정식 (1)에 대입하여 a와 b를 제거하면, (c - 4) + (3/5 × c - 4) + c = 18 c를 풀면, c = 10이 됩니다. 따라서, Chris의 나이는 10살입니다.

답) 10

233

문제) 만약 ω¹⁹⁹⁷ = 1이고 ω ≠ 1이라면, 다음을 평가하세요: 1 / (1 + ω) + 1 / (1 + ω²) + ... + 1 / (1 + ω¹⁹⁹⁷).

풀이) 다음을 고려하세요: 1 / (1 + ωᵏ) + 1 / (1 + ω¹⁹⁹⁷⁻ᵏ) = 1 / (1 + ωᵏ) + ωᵏ / (ωᵏ + ω¹⁹⁹⁷) = 1 / (1 + ωᵏ) + ωᵏ / (ωᵏ + 1) = (1 + ωᵏ) / (1 + ωᵏ) = 1. 따라서, 다음 항들을 짝지을 수 있습니다: 1 / (1 + ω), 1 / (1 + ω²), ..., 1 / (1 + ω¹⁹⁹⁵), 1 / (1 + ω¹⁹⁹⁶) 이렇게 1996 / 2 = 998 쌍으로 나누어 각 쌍의 합이 1이 되도록 합니다. 또한, 1 / (1 + ω¹⁹⁹⁷) = 1 / 2이므로, 전체 합은 998 + 1 / 2 = 1997 / 2입니다.

답) 1997 / 2

234

문제) 벡터 a와 b가 다음 조건을 만족한다고 하자: a의 크기는 2, b의 크기는 7, 그리고 a × b = (3, 2, 6). 이때, a와 b 사이의 가능한 가장 작은 각도를 도 단위로 구하시오.

풀이) θ를 a와 b 사이의 각도라고 하자. 그러면 |a × b| = |a| |b| sin(θ). 주어진 정보에 따르면, 7 = 14 sin(θ)이므로, sin(θ) = 1 / 2. 따라서, θ의 가능한 가장 작은 값은 30°이다.

답) 30°

235

문제) 함수 f가 다음과 같이 정의되어 있다고 하자: f(x) = x³ - 49x² + 623x - 2015. 함수 g(x) = f(x + 5)일 때, g의 근의 합을 구하시오.

풀이) x³ - 49x² + 623x - 2015의 근을 a, b, c라고 하자. 비에타의 정리에 따르면, a + b + c = 49이다. g(x) = f(x + 5)의 근은 a - 5, b - 5, c - 5이며, 이들의 합은 a + b + c - 15 = 49 - 15 = 34이다.

답) 34

236

문제) 다음을 계산하세요: 0.777... - 0.444... + 0.222... 답을 기약 분수로 표현하세요.

풀이) 일반적으로, 숫자 0.777...을 분수로 표현하기 위해 이를 x라고 하고 10x에서 x를 뺍니다: 10x = 7.777... - x = 0.777... ──────────── 9x = 7 이로부터 0.777... = 7 / 9임을 알 수 있습니다. 따라서, 원래 문제는 7/9 - 4/9 + 2/9를 계산하는 것으로 줄어듭니다. 결과는 5/9입니다.

답) 5/9

237

문제) 다음을 계산하세요. 1 / cos² 10° + 1 / sin² 20° + 1 / sin² 40°.

풀이) 다음을 쓸 수 있습니다. 1 / cos² 10° = 2 / (1 + cos 20°) = 2 (1 - cos 20°) / ((1 + cos 20°)(1 - cos 20°)) = 2 (1 - cos 20°) / (1 - cos² 20°) = (2 - 2 cos 20°) / sin² 20°, 따라서 1 / cos² 10° + 1 / sin² 20° + 1 / sin² 40° = (2 - 2 cos 20°) / sin² 20° + 1 / sin² 20° + 1 / sin² 40° = (3 - 2 cos 20°) / sin² 20° + 1 / sin² 40° = (4 cos² 20° (3 - 2 cos 20°)) / (4 sin² 20° cos² 20°) + 1 / sin² 40° = (12 cos² 20° - 8 cos³ 20°) / sin² 40° + 1 / sin² 40° = (12 cos² 20° - 8 cos³ 20° + 1) / sin² 40°. 삼중각 공식을 사용하면, 1/2 = cos 60° = cos (3 × 20°) = 4 cos³ 20° - 3 cos 20°, 따라서 8 cos³ 20° = 6 cos 20° + 1. 따라서, (12 cos² 20° - 8 cos³ 20° + 1) / sin² 40° = (12 cos² 20° - 6 cos 20°) / sin² 40° = (12 cos² 20° - 6 cos 20°) / (4 sin² 20° cos² 20°) = (12 cos 20° - 6) / (4 sin² 20° cos 20°) = (12 cos 20° - 6) / (4 (1 - cos² 20°) cos 20°) = (12 cos 20° - 6) / (4 cos 20° - 4 cos³ 20°) = (12 cos 20° - 6) / (4 cos 20° - 3 cos 20° - 1/2) = (12 cos 20° - 6) / (cos 20° - 1/2) = 12.

답) 12

238

문제) 양수인 x, y, z에 대해 xy = 24, xz = 48, yz = 72일 때, x + y + z를 구하세요.

풀이) 세 방정식을 모두 곱하면 x²y²z² = 82944가 됩니다. x, y, z가 양수이므로 xyz = √(82944) = 288입니다. 그러면 x = xyz / yz = 288 / 72 = 4, y = xyz / xz = 288 / 48 = 6, z = xyz / xy = 288 / 24 = 12. 따라서, x + y + z = 22입니다.

답) 22

239

문제) 실수 값 중에서 다음 함수의 정의역에 포함되지 않는 x 값은 무엇입니까? f(x) = 1 / (|x² + 3x - 4| + |x² + 9x + 20|)

풀이) 함수 f의 정의역에 포함되지 않는 x 값은 분모가 0이 되는 경우입니다. 두 절대값은 음수가 될 수 없으므로, 분모가 0이 되려면 두 절대값이 모두 0이어야 합니다. 따라서, 0 = x² + 3x - 4 = (x + 4)(x - 1) ⇒ x = -4 또는 x = 1 0 = x² + 9x + 20 = (x + 4)(x + 5) ⇒ x = -4 또는 x = -5 두 절대값이 모두 0이 되는 유일한 x 값은 x = -4입니다.

답) -4

240

문제) 직선 y=ax+c, y=ax+d, y=bx+c, y=bx+d로 경계 지어진 평행사변형의 넓이가 18입니다. 직선 y=ax+c, y=ax-d, y=bx+c, y=bx-d로 경계 지어진 평행사변형의 넓이가 72입니다. a, b, c, d가 양의 정수일 때, a+b+c+d의 가능한 가장 작은 값은 무엇입니까?

풀이) 첫 번째 평행사변형의 두 꼭짓점은 (0, c)와 (0, d)에 있습니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.5 cm);

pair P, Q, R, S;

P = (0,9);
Q = (3,12);
R = (0,3);
S = (-3,0);

draw(interp(P,Q,-0.4)--interp(P,Q,1.4));
draw(interp(R,S,-0.4)--interp(R,S,1.4));
draw(interp(P,S,-0.2)--interp(P,S,1.2));
draw(interp(Q,R,-0.2)--interp(Q,R,1.2));

label("$y = ax + c$", interp(S,R,1.4), E);
label("$y = ax + d$", interp(P,Q,1.4), E);
label("$y = bx + c$", interp(Q,R,1.2), SE);
label("$y = bx + d$", interp(P,S,1.2), SE);

dot("$(0,c)$", R, SE);
dot("$(0,d)$", P, NW);

다른 두 꼭짓점의 x-좌표는 ax+c=bx+d와 ax+d=bx+c를 만족하므로, x-좌표는 ±(c-d)/(b-a)입니다. 따라서 평행사변형은 두 삼각형으로 구성되며, 각 삼각형의 넓이는 9 = 1/2 · |c-d| · |(c-d)/(b-a)| 입니다. 따라서 (c-d)² = 18|b-a|입니다. 두 번째 평행사변형에 대해서도 비슷한 논리를 적용하면, (c+d)² = 72|b-a|입니다. 첫 번째 식에서 두 번째 식을 빼면 4cd = 54|b-a|가 되어, 2cd = 27|b-a|입니다. 따라서 |b-a|는 짝수이고, a+b가 최소가 되려면 {a,b}={1,3}입니다. 또한, cd는 27의 배수이고, c+d가 최소가 되려면 {c,d}={3,9}입니다. 따라서 a+b+c+d의 가능한 가장 작은 값은 1+3+3+9=16입니다. (a,b,c,d)=(1,3,3,9)일 때 조건이 만족됩니다.

답) 16

241

문제) 도형에서, PT는 QR과 평행합니다. ∠PQR의 크기는 몇 도입니까? 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0),black+linewidth(1));
draw((0,0)--(10,0),MidArrow);
draw((10,0)--(20,0),black+linewidth(1));
draw((0,0)--(-7,10)--(7,10)--(10,0),black+linewidth(1));
draw((-5,10)--(7,10),MidArrow);
label("$x^{\circ}$",(-6,10),SE);
label("$2x^{\circ}$",(7,10),SW);
label("$128^{\circ}$",(10,0),NE);
label("$P$",(-7,10),N);
label("$T$",(7,10),N);
label("$R$",(10,0),S);
label("$Q$",(0,0),S);

풀이) PT와 RQ가 평행하므로, 2x° = 128°입니다. 따라서 x = 64이고, ∠TPQ = 64°입니다. 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0),black+linewidth(1));
draw((0,0)--(10,0),MidArrow);
draw((10,0)--(20,0),black+linewidth(1));
draw((0,0)--(-7,10)--(7,10)--(10,0),black+linewidth(1));
draw((-5,10)--(7,10),MidArrow);
label("$x^{\circ}$",(-6,10),SE);
label("$2x^{\circ}$",(7,10),SW);
label("$128^{\circ}$",(10,0),NE);
label("$P$",(-7,10),N);
label("$T$",(7,10),N);
label("$R$",(10,0),S);
label("$Q$",(0,0),S);

PT와 QR이 평행하므로, ∠TPQ와 ∠PQR는 보각입니다. 따라서 ∠PQR + 64° = 180°이고, ∠PQR = 116°입니다.

답) 116

242

문제) 원점과 그래프 y = 1 / 2x² - 9 위의 한 점 사이의 가장 짧은 거리를 a라고 할 때, a²를 구하세요.

풀이) 거리 공식을 사용하여, 우리는 √(x² + y²) = sqrt{x² + 1 / 4x⁴ - 9x² + 81}를 최소화하려고 합니다. 일반적으로 이러한 최소화 문제는 미적분을 필요로 하지만, 때때로 작동하는 최적화 방법 중 하나는 완전제곱을 시도하는 것입니다. 루트 안에서 1 / 4를 인수로 꺼내면 다음과 같습니다. 1 / 2√(4x² + x⁴ - 36x² + 324) = 1 / 2√((x⁴ - 32x² + 256) + 68) = 1 / 2√((x² - 16)² + 68) 이 마지막 표현은 제곱이 0이 될 때 최소화되며, 즉 x² = 16일 때입니다. 그러면 거리는 √(68) / 2 = √(17)입니다. 따라서 원하는 답은 √(17)² = 17입니다.

답) 17

243

문제) 정부 채권에 24,000달러를 투자했으며, 이 채권은 두 달마다 1%의 이자를 지급합니다 (즉, 투자금은 두 달마다 1% 증가합니다). 5년 후, 이 투자에서 총 몇 달러가 될까요? 답을 가장 가까운 정수로 표현하세요.

풀이) 5년은 60개월이므로, 이자는 30번 복리로 계산됩니다. 따라서 투자는 24,000달러 × 1.01³⁰ ≈ 32,348달러로 증가합니다. 이는 가장 가까운 달러로 표현한 값입니다.

답) 32,348달러

244

문제) 한 삼각형의 두 변의 길이가 각각 1 단위와 3 단위입니다. 세 번째 변의 길이는 정수 단위입니다. 세 번째 변의 길이는 몇 단위입니까?

풀이) 세 번째 변의 길이를 n이라고 합시다. 삼각형의 부등식에 따르면, 1 + 3 > n 그리고 1 + n > 3이므로, 2 < n < 4입니다. 이 조건을 만족하는 유일한 정수 n은 3입니다.

답) 3

245

문제) 한 볼록 다각형에서 한 내각을 제외한 모든 내각의 합이 1070도일 때, 이 다각형은 몇 개의 변을 가질까요?

풀이) n각형의 내각의 합은 180(n-2)도입니다. 따라서, 7각형의 내각의 합은 180(7-2) = 900도이므로, 원하는 다각형은 7개 이상의 변을 가집니다. 한편, 8각형의 내각의 합은 180(8-2) = 1080도입니다. 따라서, 이 다각형은 8개의 변을 가질 수 있으며, 마지막 각의 크기는 10도입니다. 이것이 유일한 가능성임을 확인하기 위해, 9각형의 내각의 합은 180(9-2) = 1260도입니다. 따라서, 다각형이 8개 이상의 변을 가진다면, 마지막 내각은 최소 1260도 - 1070도 = 190도가 되어야 합니다. 그러나 이는 불가능합니다. 왜냐하면 볼록 다각형의 각 내각은 180도 미만이어야 하기 때문입니다.

답) 8

246

문제) 함수 f(x) = x¹⁰ + 5x⁹ - 8x⁸ + 7x⁷ - x⁶ - 12x⁵ + 4x⁴ - 8x³ + 12x² - 5x - 5가 주어졌습니다. 긴 나눗셈을 사용하지 않고, f(x)를 x² - 1로 나눌 때의 나머지를 구하세요.

풀이) f(x) = q(x)(x² - 1) + r(x)로 쓸 수 있습니다. 여기서 q(x)는 몫이고 r(x)는 나머지입니다. x² - 1은 2차식이므로 나머지는 최대 1차식입니다. 따라서 r(x) = ax + b로 쓸 수 있습니다. x² - 1의 근은 x = -1과 x = 1입니다. 따라서 f(1) = r(1)이고 f(-1) = r(-1)입니다. 주어진 f(x) 식을 사용하여 f(1) = -10과 f(-1) = 16을 계산할 수 있습니다. 따라서 다음과 같은 방정식 시스템을 얻습니다: -10 = a · (1) + b, 16 = a · (-1) + b. 이 두 방정식을 더하면 6 = 2b가 되고, 따라서 b = 3입니다. 어느 한 방정식에 대입하면 a = -13이 됩니다. 따라서, r(x) = ax + b = -13x + 3입니다.

답) -13x + 3

247

문제) 12명의 친구들이 Oscar's Overstuffed Oyster House에서 저녁을 먹기 위해 만났고, 각자 한 끼씩 주문했습니다. 음식의 양이 너무 많아서 18명에게 충분할 정도였습니다. 만약 그들이 음식을 나눠 먹는다면, 12명에게 딱 맞는 양의 음식을 주문하려면 몇 끼를 주문해야 할까요?

풀이) 12명이 18 / 12 = 1.5배 너무 많은 음식을 주문했다면, 그들은 12 / 1.5 = 2/3 × 12 = 8 끼를 주문했어야 합니다.

답) 8

248

문제) 정수 계수를 가진 이차 다항식 p(x)가 4-√(11)을 근으로 가질 때, p(3) / p(4)의 값을 구하시오.

풀이) 다항식 p(x)가 정수 계수를 가지므로 (특히 유리수 계수를 가지므로), 4-√(11)의 다른 근은 그 복소수 공액인 4+√(11)이어야 합니다. 따라서 p(x)는 다음과 같은 형태를 가집니다. p(x) = A(x-(4-√(11)))(x-(4+√(11))) 여기서 A는 0이 아닌 상수입니다. 따라서 p(3) = A(-1+√(11))(-1-√(11)) = -10A 그리고 p(4) = A(√(11))(-√(11)) = -11A 이므로 p(3) / p(4) = -10A / -11A = 10 / 11.

답) 10 / 11

249

문제) 주어진 행렬 A = ((3, 7), (-1, -2)) 에 대해, A²⁷ + A³¹ + A⁴⁰를 계산하세요.

풀이) 행렬 A² = ((2, 7), (-1, -3)) 이고, 행렬 A³ = AA² = ((-1, 0), (0, -1)) = -I입니다. 따라서, A²⁷ + A³¹ + A⁴⁰ = (A³)⁹ + (A³)¹⁰ A + (A³)¹³ A = (-I)⁹ + (-I)¹⁰ A + (-I)¹³ A = -I + A - A = -I = ((-1, 0), (0, -1)).

답) ((-1, 0), (0, -1))

250

문제) 0 홀수 정수 t를 찾으세요.

풀이) 각 후보 t에 대해 t · (t + 2) ≡ 1 (mod 23)인지 시험해보는 방법으로 답을 찾을 수 있습니다. 그러나 다른 방법도 있습니다. 4 · 6 = 24 ≡ 1 (mod 23)이므로, 4는 역원이 자신보다 2 큰 수라는 주요 조건을 충족합니다. 불행히도, 4는 홀수가 아닙니다. 하지만 다음과 같이 계산할 수 있습니다: (-4) · (-6) = 4 · 6 ≡ 1 (mod 23) 따라서 -4와 -6은 서로의 역원입니다 (mod 23). -4 ≡ 19 (mod 23)이고 -6 ≡ 17 (mod 23)이므로, 문제의 요구 조건을 만족하는 답은 t = 17입니다. (17 · 19 = 323 = 14 · 23 + 1임을 확인할 수 있습니다.)

답) 17

251

문제) 만약 a가 x-절편이고, b가 y-절편이며, m이 직선의 기울기일 때, 직선의 방정식이 x/4 + y/12 = 1이라면, a + b + m의 값은 얼마입니까?

풀이) x-절편을 찾기 위해 y=0을 방정식에 대입합니다. 그러면 x/4 = 1이 되어 x = 4가 됩니다. 따라서 a=4입니다. 마찬가지로 x=0을 대입하면 y/12 = 1이 되어 y=12가 됩니다. 따라서 b=12입니다. 기울기를 찾는 방법은 여러 가지가 있습니다. 먼저, 방정식을 기울기-절편 형태로 변형할 수 있습니다. 양변에서 x/4를 빼고 12를 곱하면 y = -3x + 12가 됩니다. 이는 기울기가 -3임을 알려주며, y-절편이 12임을 확인시켜 줍니다. 또한, 이미 (4,0)과 (0,12)가 직선 위에 있다는 것을 보였으므로, 직선의 기울기는 (12 - 0) / (0 - 4) = -3입니다. 따라서 원하는 합은 4 + 12 - 3 = 13입니다.

답) 13

252

문제) 여섯 대의 차가 한 번에 하나씩 빨간 신호등에 도착합니다. 신호등에는 세 개의 차선이 있으며, 하나는 좌회전 차선, 하나는 직진 차선, 하나는 우회전 차선입니다. 모든 차선이 점유되도록 차들이 쌓이는 방법은 몇 가지입니까? 첫 번째 차가 좌회전을 하고 두 번째 차가 직진하는 경우는 첫 번째 차가 직진하고 두 번째 차가 좌회전하는 경우와 다르게 간주됩니다. 즉, 차들은 구별 가능하지만 교차로에 도착하는 순서는 고정되어 있습니다.

풀이) 어떤 차선이 비어 있을 수 있는 경우의 수를 계산하고, 총 경우의 수 3⁶ = 729에서 이를 뺍니다. 각 운전자는 세 가지 선택이 있기 때문입니다. 좌회전 차선이 비어 있는 경우를 가정합니다. 그러면 각 운전자는 2가지 선택으로 제한되며, 좌회전 차선을 비워두는 방법은 2⁶가지가 있습니다. 같은 논리로 중앙 차선과 우회전 차선을 비워두는 방법도 2⁶가지가 있습니다. 그러나 두 개의 차선이 비어 있는 경우를 중복 계산했습니다. 다행히도 각 운전자는 세 번째 차선으로 가야 하므로, 우리가 과대 계산한 경우는 3가지뿐입니다. 따라서 최소한 하나의 차선이 비어 있는 경우는 3·2⁶ - 3=189가지이며, 모든 차선이 점유되는 경우는 729-189 = 540가지입니다.

답) 540

253

문제) 모든 실수 x에 대해, 4(x + 7)(2 - x)의 최대값은 얼마입니까?

풀이) y = 4(x + 7)(2 - x)의 그래프는 포물선입니다. y = 0일 때, x = -7과 x = 2이므로, 포물선의 x절편은 (-7,0)과 (2,0)입니다. 포물선의 꼭짓점이 (h,k)라면, x절편 (-7,0)과 (2,0)은 선 x = h를 기준으로 대칭이므로, h = (-7 + 2) / 2 = -5 / 2입니다. 따라서, y = 4(x + 7)(2 - x)의 최대값은 x = -5 / 2일 때 발생하며, 이 경우 y = 4(-5 / 2 + 7)(2 + 5 / 2) = 4 · 9 / 2 · 9 / 2 = 81입니다. (이는 최대값이며, 최소값이 아님을 주의하세요. 왜냐하면 y = 4(x + 7)(2 - x) = -4x² - 20x + 56에서 x²의 계수가 음수이기 때문입니다.)

답) 81

254

문제) 3인치는 2피트의 몇 분의 몇입니까? 답을 기약 분수로 표현하세요.

풀이) 2피트는 2 · 12 = 24인치이므로, 3인치는 3 / 24 = 1/8로 2피트의 1/8입니다.

답) 1/8

255

문제) Pat는 초콜릿 칩, 오트밀, 땅콩 버터 쿠키만 있는 쟁반에서 6개의 쿠키를 선택하려고 합니다. 이 세 종류의 쿠키는 각각 최소 6개 이상 있습니다. 6개의 쿠키를 선택할 수 있는 서로 다른 조합은 몇 가지입니까? (같은 종류의 쿠키는 구별할 수 없습니다.)

풀이) 세 종류의 쿠키 수의 합이 6이 되어야 합니다. 합이 6이 되는 가능한 정수 집합은 다음과 같습니다: 0,0,6; 0,1,5; 0,2,4; 0,3,3; 1,1,4; 1,2,3; 그리고 2,2,2. 각 집합의 순서를 바꾸면 다른 쿠키 조합이 결정됩니다. 다음 집합 각각에 대해 3가지 순서가 있습니다: 0,0,6; 0,3,3; 그리고 1,1,4. 다음 집합 각각에 대해 6가지 순서가 있습니다: 0,1,5; 0,2,4; 그리고 1,2,3. 2,2,2는 순서가 하나뿐입니다. 따라서 6개의 쿠키 조합의 총 수는 3×3 + 3×6 + 1 = 28입니다.

답) 28

256

문제) 다음 방정식으로 정의된 곡선을 찾으세요. r² cos 2θ = 4 (A) 직선 (B) 원 (C) 포물선 (D) 타원 (E) 쌍곡선 정답의 문자를 입력하세요.

풀이) r² cos 2θ = 4에서, r² (cos² θ - sin² θ) = r² cos² θ - r² sin² θ = 4입니다. 그러면 x² - y² = 4, 또는 x² / 4 - y² / 4 = 1입니다. 따라서, 그래프는 쌍곡선을 나타냅니다. 정답은 (E)입니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.5 cm);

pair moo (real t) {
 real r = sqrt(4/Cos(2*t));
 return (r*Cos(t), r*Sin(t));
}

path foo = moo(-44);
real t;

for (t = -44; t <= 44; t = t + 0.1) {
 foo = foo--moo(t);
}

draw(foo,red);
draw(reflect((0,0),(0,1))*(foo),red);

draw((-4,0)--(4,0));
draw((0,-4)--(0,4));

limits((-4,-4),(4,4),Crop);

label("$r^2 \cos 2 \theta = 4$", (6.5,1.5), red);

답) (E)

257

문제) 다음을 간단히 하세요: 1/5 · 8/7 ÷ 12/20.

풀이) 먼저, 나눗셈 규칙을 사용하여 분수의 곱셈만 있는 식으로 변환할 수 있습니다. 따라서 1/5 · 8/7 ÷ 12/20 = 1/5 · 8/7 · 20/12가 됩니다. 이제 5와 20은 공약수 5를 가지고 있고, 8과 12는 공약수 4를 가지고 있음을 알 수 있습니다. 따라서 다음과 같이 간단히 할 수 있습니다: 1/5 · 8/7 · 20/12 = 1/5 · 2/7 · 4/3 = (1 · 2 · 4) / (7 · 3) = 8/21.

답) 8/21

258

문제) 부피가 1 세제곱 피트인 정육면체의 총 표면적은 몇 제곱 인치입니까?

풀이) 기억하세요: 1 피트 = 12 인치. 따라서 1 피트² = 12² 인치² = 144 인치². 마지막으로, 부피 V = l × w × h, 즉 부피는 길이, 너비, 높이의 곱입니다. 정육면체의 경우 길이, 높이, 너비가 모두 같으므로 주어진 정육면체의 한 변의 길이는 1 피트입니다. 정육면체는 6개의 면을 가지고 있으므로, 정육면체의 표면적은 6 × (1 피트 × 1 피트) = 6 피트² 입니다. 이제 변환합니다: 6 피트² × (144 인치² / 1 피트²) = 864 인치². 따라서 최종 답은 864 인치²입니다.

답) 864 인치²

259

문제) 저는 노란 구슬과 파란 구슬이 들어 있는 가방을 가지고 있습니다. 현재 파란 구슬과 노란 구슬의 비율은 4:3입니다. 만약 제가 파란 구슬 5개를 추가하고 노란 구슬 3개를 제거하면, 비율은 7:3이 됩니다. 제가 더 추가하기 전에 가방에 있던 파란 구슬은 몇 개였습니까?

풀이) x를 제가 더 추가하기 전의 파란 구슬의 개수, y를 노란 구슬의 개수라고 합시다. 파란 구슬과 노란 구슬의 비율이 4:3이라는 조건이 주어졌으므로, x / y = 4 / 3입니다. 또한, 파란 구슬을 추가하고 노란 구슬을 제거한 후의 파란 구슬과 노란 구슬의 총 개수는 각각 x + 5와 y - 3이 됩니다. 이 시점에서 비율이 7:3이 된다는 조건이 주어졌으므로, (x + 5) / (y - 3) = 7 / 3입니다. 첫 번째 방정식을 교차 곱하면 3x = 4y가 되고, 두 번째 방정식을 교차 곱하면 3(x + 5) = 7(y - 3)이 됩니다. 두 개의 연립 방정식을 풀면 y = 12, x = 16이라는 해를 얻습니다. x는 더 추가하기 전의 파란 구슬의 개수를 나타내므로, 문제의 답은 16입니다.

답) 16

260

문제) 수 5+√(3)와 그 근호 켤레의 곱을 계산하세요.

풀이) 이 수의 근호 켤레는 5-√(3)입니다. 따라서 두 수의 곱은 다음과 같습니다: (5+√(3))(5-√(3)) = 5² - (√(3))² = 25 - 3 = 22.

답) 22

261

문제) 점 A = (1, -11, 2), B = (3, -4, 1), C = (-2, 1, -1)일 때, ∠ABC를 도 단위로 구하세요.

풀이) 거리 공식을 사용하여 AB = 3√(6), AC = 9√(2), BC = 3√(6)임을 계산합니다. 코사인 법칙에 따르면, cos ∠ABC = ((3√(6))² + (3√(6))² - (9√(2))²) / (2 · 3√(6) · 3√(6)) = -1/2. 따라서, ∠ABC = 120°입니다.

답) 120°

262

문제) 삼각형 △ABC에서 ∠A = 14°이고, AB가 지름인 원에 내접해 있습니다. ∠B는 몇 도입니까?

풀이) AB가 지름이라면, 삼각형은 C에서 직각을 가집니다. 따라서, ∠B = 180° - (∠A + ∠C) = 180° - (14° + 90°) = 76°.

답) 76°

263

문제) 만약 10ˣ - 10 = 9990이라면, x는 무엇과 같습니까?

풀이) 10ˣ - 10 = 9990이므로, 10ˣ = 9990 + 10 = 10000입니다. 10ˣ = 10000이라면, 10000은 네 개의 0으로 끝나므로 x = 4입니다.

답) 4

264

문제) 정다각형에서 내각의 크기가 외각의 크기의 6.5배입니다. 이 다각형의 변의 수는 몇 개입니까?

풀이) 정 n각형의 내각의 크기는 180(n-2)/n 도이고, 외각의 크기는 360/n 도입니다. 다음 식을 풀어보면, 180(n-2)/n = 6.5 · (360/n) n = 15임을 알 수 있습니다.

답) 15

265

문제) 아래 그림에서 사각형 CDEG는 정사각형이며 CD = 3입니다. 사각형 BEFH는 직사각형입니다. BE = 5일 때, BH는 몇 단위입니까? 답을 대분수로 표현하세요. 아래는 도형을 그리는 코드입니다.

unitsize(5mm);
defaultpen(linewidth(.7pt)+fontsize(8pt));

pair A=(0,0), B=(3,0), C=(6,0), D=(9,0), Ep=(9,3), G=(6,3);
pair F0=bisectorpoint(B,2*Ep-B), H0=bisectorpoint(Ep,2*B-Ep);
pair H=extension(B,H0,A,G);
pair F=extension(Ep,F0,A,G);

draw(H--B--Ep--F--A--D--Ep--G--C);
label("$A$",A,S);
label("$B$",B,S);
label("$C$",C,S);
label("$D$",D,S);
label("$E$",Ep,E);
label("$F$",F,N);
label("$G$",G,NW);
label("$H$",H,NW);

풀이) BE와 GC의 교차점을 J라고 하자. 아래는 도형을 그리는 코드입니다.

unitsize(5mm);
defaultpen(linewidth(.7pt)+fontsize(8pt));
pair A=(0,0), B=(3,0), C=(6,0), D=(9,0), Ep=(9,3), G=(6,3), K=(33/5,9/5);
pair F0=bisectorpoint(B,2*Ep-B), H0=bisectorpoint(Ep,2*B-Ep);
pair H=extension(B,H0,A,G);
pair F=extension(Ep,F0,A,G);
pair J=extension(B,Ep,G,C);
draw(H--B--Ep--F--A--D--Ep--G--C);
draw(G--K);
label("$A$",A,S);
label("$B$",B,S);
label("$C$",C,S);
label("$D$",D,S);
label("$E$",Ep,E);
label("$F$",F,N);
label("$G$",G,NW);
label("$H$",H,NW);
label("$J$",J,NW);
label("$K$",K,SE);

BD = √(BE² - DE²) = √(5² - 3²) = 4 단위입니다. 삼각형 BCJ와 BDE의 유사성에 의해, CJ / (4 - 3) = 3 / 4 대입 후 CJ = 3 / 4를 구할 수 있으며, 이는 GJ = 3 - 3 / 4 = 9 / 4를 의미합니다. 피타고라스 정리를 삼각형 GJE에 적용하면, EJ = √(3² + (9 / 4)²) = 15 / 4입니다. G에서 EJ의 변에 수직인 발을 K라고 정의합니다. 삼각형 GKJ와 EGJ의 유사성에 의해, GK / GJ = EG / EJ GK / (9 / 4) = 3 / (15 / 4) 이를 풀면 GK = 9 / 5입니다. GKBH는 직사각형이므로, BH = GK = 9 / 5 = 1과 4/5 단위입니다.

답) 1과 4/5

266

문제) 홀수 수열 1, 3, 5, 7, ...의 2003번째 항은 무엇입니까?

풀이) 홀수 수열 1, 3, 5, 7, ...은 공차가 2인 등차수열입니다. 따라서 2003번째 항은 1 + 2002 · 2 = 4005입니다.

답) 4005

267

문제) 1부터 100까지의 숫자 중에서 무작위로 하나의 숫자를 선택합니다. 이 숫자가 3의 배수일 확률은 얼마입니까?

풀이) 1부터 100까지 가능한 숫자는 총 100개입니다. 1부터 100까지 3의 배수는 총 33개입니다: (3, 6, 9, ..., 99) = (1×3, 2×3, 3×3, ..., 33×3). 따라서 무작위로 선택된 숫자가 3의 배수일 확률은 33 / 100입니다.

답) 33 / 100

268

문제) 원 J에서, HO와 HN은 각각 O와 N에서 원에 접합니다. m∠J와 m∠H의 합의 각도를 구하세요. 아래는 도형을 그리는 코드입니다.

size(150);
import graph;
pair J = (0,0), H = (6,0), O, N;
path circ = Circle(J,3);
pair M = midpoint(J--H);
path secCirc = Circle(M,3);
pair[] tangentPoints = intersectionpoints(circ,secCirc);
O = tangentPoints[0]; N = tangentPoints[1];
draw(J--N--H--O--cycle);
draw(circ);
label("$H$",H,E);
label("$J$",J,W);
label("$N$",N,S);
label("$O$",O,NE);

풀이) OH와 NH는 각각 O와 N에서 원의 반지름에 접하므로, ∠O = ∠N = 90°. 사각형 JOHN의 내각의 합은 360°이므로, ∠J + ∠H = 360° - ∠O - ∠N = 180°.

답) 180°

269

문제) 1 + 2 + 3 + 4 + ... + 9 + 10을 9로 나눌 때 나머지는 얼마입니까?

풀이) 합을 살펴보면, 숫자 1부터 8까지는 9를 이루는 쌍으로 묶을 수 있습니다. 즉, 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 = 9입니다. 따라서 남는 항은 9와 10뿐이며, 9는 9로 나누어 떨어지므로 10을 9로 나눌 때의 나머지만 찾으면 됩니다. 그 나머지는 1입니다.

답) 1

270

문제) 한 수학 천재가 구별할 수 없는 IMO 금메달 2개와 구별할 수 없는 IPhO 금메달 2개를 한 줄에 놓으려고 합니다. 가능한 서로 다른 배열의 수는 몇 개입니까?

풀이) 줄에는 4개의 슬롯이 있습니다. 그는 IMO 메달을 놓을 두 개의 슬롯을 선택할 수 있으며, 이는 4개 중 2개를 선택하는 경우의 수로 6가지입니다.

답) 6

271

문제) 한 공연의 티켓 한 장의 정가는 20입니다. 수잔은 25% 할인 쿠폰을 사용하여 4장의 티켓을 구매합니다. 팸은 30% 할인 쿠폰을 사용하여 5장의 티켓을 구매합니다. 팸이 수잔보다 몇 달러 더 지불했습니까?

풀이) 수잔과 팸이 각각 지불한 총 구매 금액을 계산해야 합니다. 수잔은 4장의 티켓을 25% 할인받아 구매했습니다: 4 × 20 = 80. 25% 할인으로, 그녀는 80 × 0.75 = 60를 지불했습니다. 팸은 5장의 티켓을 30% 할인받아 구매했습니다: 5 × 20 = 100. 30% 할인으로, 그녀는 100 × 0.70 = 70를 지불했습니다. 따라서 팸은 수잔보다 70 - 60 = 10을 더 지불했습니다.

답) 10

272

문제) 997의 모듈로 1000에 대한 역수를 계산하세요. 답을 0에서 999 사이의 정수로 표현하세요.

풀이) 우리는 997 ≡ -3 (mod 1000)임을 알 수 있습니다. 그리고 (-3) · 333 = -999 = -1000 + 1 ≡ 1 (mod 1000)입니다. 따라서, 997 · 333 ≡ 1 (mod 1000)이므로, 997의 모듈로 1000에 대한 역수는 333입니다.

답) 333

273

문제) 0.1331을 분수 a / b로 나타낼 때, 여기서 a와 b는 양의 정수이고 최대공약수가 1입니다. 이때 a+b는 얼마입니까?

풀이) x = 0.1331이라고 하자. 그러면 10000x = 1331.1331이 됩니다. 따라서 9999x = 1331이므로, x = 1331 / 9999입니다. 분자와 분모에서 11을 공약수로 나눌 수 있으므로, x = 121 / 909입니다. 따라서 a+b = 121 + 909 = 1030입니다.

답) 1030

274

문제) 1992년, 이탈리아에서 젤라토 한 스쿱은 1200 리라에 구매할 수 있었습니다. 같은 젤라토가 미국에서는 1.50에 해당했습니다. 리라와 달러의 환율에 따라, 1,000,000 리라는 몇 달러에 해당할까요?

풀이) 양변에 1200 리라 = 1.50를 1,000,000 / 1200으로 곱하면, 백만 리라는 (3 / 2) · 10,000 / 12 = 1250 달러가 됩니다.

답) 1250

275

문제) 정사각형의 변의 길이가 2 단위인 정규 9각형 내부의 모든 점의 집합과 9각형의 둘레에 있는 점에서 1 단위 미만 떨어진 모든 점의 집합의 합집합을 S라고 하자. S의 둘레는 몇 단위인가?

풀이) S는 약간 둥근 모서리를 가진 9각형처럼 보입니다. 우리는 9각형의 인접한 변을 그리고 S의 경계를 살펴봅니다. 아래는 도형을 그리는 코드입니다.

size(200);
draw((-7.66,-6.43)--(0,0)--(10,0)--(17.66,-6.43));
draw((0,5)--(10,5),blue); draw((13.21,3.83)--(20.87,-2.60),blue);
draw(Arc((10,0),5,50,90),red); draw(Arc((0,0),5,90,130),red);
draw((10,0)--(10,5),dashed); draw((0,0)--(0,5),dashed);
draw((10,0)--(13.21,3.83),dashed);
label("2",(5,0),S); label("1",(10,2.5),W);
draw((-3.21,3.83)--(-10.87,-2.60),blue);
draw((-3.21,3.83)--(0,0),dashed);

S의 외부에 있는 부분을 9개의 직사각형과 9개의 원호로 나눌 수 있으며, 따라서 S의 둘레는 교대로 직선(위 그림에서 파란색)과 곡선(위 그림에서 빨간색)으로 구성됩니다. S의 둘레는 9개의 파란 선과 9개의 빨간 호로 구성됩니다. 각 직사각형의 변의 길이는 1과 2이므로 각 파란 선은 2 단위 길이이고, 파란 부분의 둘레의 총 길이는 2×9 = 18 단위입니다. 9각형의 각 꼭짓점 주위에서, 내부 각도, 두 직각, 원호의 각도가 합쳐져 360도가 됩니다. 9각형의 내부 각도는 각각 180(9-2)/9 = 140도입니다. 따라서 각 원호의 각도는 360-90-90-140 = 40도입니다. 각 원호의 반지름은 1이고 호의 길이는 (40°/360°)×2×π×1 = (2π)/9이므로, 이 9개의 원호의 총 호의 길이는 2π입니다. (이는 반지름이 1인 원의 둘레와 같습니다. 이는 9개의 원호가 합쳐진 것입니다.) 마지막으로, S의 둘레는 18 + 2π 단위입니다.

답) 18 + 2π

276

문제) 함수 f(x) = 2x - 3과 g(x) = x + 1이 주어졌습니다. g(f(5) - 1)의 값을 구하세요.

풀이) f(5) = 2 × 5 - 3 = 7이므로, g(f(5) - 1) = g(7 - 1) = g(6) = 6 + 1 = 7입니다.

답) 7

277

문제) 얼마나 많은 실수 값의 x에 대해 √(120 - √(x))가 정수입니까?

풀이) k = √(120 - √(x))가 정수라고 가정합시다. 그러면 0 ≤ k ≤ √(120)이고, k가 정수이므로 0 ≤ k ≤ 10입니다. 따라서 k의 가능한 정수 값은 11개입니다. 각 k에 대해, x의 대응 값은 (120 - k²)²입니다. (120 - k²)²는 0 ≤ k ≤ 10에서 양수이고 감소하므로, x의 값은 서로 다릅니다. 따라서 x의 가능한 값은 총 11개입니다.

답) 11

278

문제) √(53)를 가장 간단한 근호 형태로 나타내세요.

풀이) 53은 소수이므로, √(53)은 이미 가장 간단한 근호 형태입니다.

답) √(53)

279

문제) 가장 큰 8자리 2진수는 무엇인가요? 답을 10진수로 표현하세요.

풀이) 가장 큰 8자리 2진수는 가장 작은 9자리 2진수보다 1 작습니다. 이는 100000000₂ = 1 · 2⁸ = 256입니다. 따라서, 가장 큰 8자리 2진수는 256 - 1 = 255입니다.

답) 255

280

문제) 도형에서 세 개의 동심원이 각각 반지름 4, 6, 7을 가지고 있습니다. 세 개의 영역이 아래에 X, Y, Z로 표시되어 있습니다. 이 세 영역 중에서 가장 큰 면적을 가진 영역과 가장 작은 면적을 가진 영역의 면적 차이는 얼마입니까? 답을 정확한 형태로 표현하세요. 아래는 도형을 그리는 코드입니다.

import graph;
filldraw(circle((0,0),7), lightgray, black+linewidth(1));
filldraw(circle((0,0),6), gray, black+linewidth(1));
filldraw(circle((0,0),4), white, black+linewidth(1));
dot((0,0));
label("$X$",(2,0));
label("$Y$",(5,0));
label("$Z$",(6.5,0));

풀이) 내부 원 (영역 X)의 면적은 π · 4² = 16π입니다. 유사한 방법으로, 중간 고리 (영역 Y)의 면적은 π · 6² - π · 4² = 36π - 16π = 20π입니다. 또한, 외부 고리 (영역 Z)의 면적은 π · 7² - π · 6² = 49π - 36π = 13π입니다. 따라서, 영역 Y가 가장 큰 면적을 가지고 있고, 영역 Z가 가장 작은 면적을 가지고 있습니다. 이들의 면적 차이는 20π - 13π = 7π입니다.

답) 7π

281

문제) a와 b가 2보다 큰 서로 다른 소수라고 가정합시다. 정수 a(2a+b)-2a²+ab의 전체 약수는 몇 개입니까?

풀이) 분배법칙을 사용하고 같은 항을 결합하면, a(2a+b)-2a²+ab = 2a²+ab-2a²+ab = 2ab가 됩니다. 이제 a와 b는 2보다 큰 서로 다른 소수이므로, 2ab = 2¹·a¹·b¹는 (1+1)(1+1)(1+1) = 8개의 약수를 가집니다.

답) 8

282

문제) 정오각형 FGHIJ에서, 오각형의 변을 연장하여 별 모양을 형성합니다. 그림에서 각 A의 크기는 얼마입니까? 아래는 도형을 그리는 코드입니다.

draw((-42.4,30.8)--(-10,30.8)--(0,63.2)--(10,30.8)--(42.4,30.8)--(16.2,11.8)--(24.9,-18.1)--(0,0)--(-24.9,-18.1)--(-16.2,11.8)--cycle,linewidth(1));
draw((-10,30.8)--(10,30.8)--(16.2,11.8)--(0,0)--(-16.2,11.8)--cycle,linewidth(1));
label("$A$",(-42.4,30.8),W);
label("$F$",(-10,30.8),NW);
dot((-10,30.8));
label("$G$",(10,30.8),NE);
dot((10,30.8));
label("$H$",(16.2,11.8),E);
dot((16.2,11.8));
label("$I$",(0,0),S);
dot((0,0));
label("$J$",(-16.2,11.8),WSW);
dot((-16.2,11.8));

풀이) 오각형의 각도 합은 180(5-2) = 540도이므로, 정오각형 FGHIJ의 각 내부 각도는 540도 / 5 = 108도입니다. 특히, ∠JFG = 108도이므로 ∠AFJ = 180도 - ∠JFG = 180도 - 108도 = 72도입니다. 마찬가지로, ∠AJF = 180도 - 108도 = 72도입니다. 마지막으로, 삼각형 AFJ의 각도 합은 180도이므로 ∠FAJ = 180도 - ∠AFJ - ∠AJF = 180도 - 72도 - 72도 = 36도입니다.

답) 36도

283

문제) 수열 0, 1, 1, 3, 6, 9, 27, ...에서 첫 번째 항은 0입니다. 이후의 항들은 1부터 시작하는 각 연속된 정수로 번갈아 가며 더하고 곱하여 생성됩니다. 예를 들어, 두 번째 항은 첫 번째 항에 1을 더하여 생성되고, 세 번째 항은 두 번째 항에 1을 곱하여 생성됩니다. 네 번째 항은 세 번째 항에 2를 더하여 생성됩니다. 이와 같은 방식으로 진행됩니다. 125보다 큰 첫 번째 항의 값은 무엇입니까?

풀이) 이 수열을 27에서 계속하면, 4를 더하여 31을 만들고, 31에 4를 곱하여 124를 만듭니다. 그런 다음 124에 5를 더하여 129를 만듭니다. 따라서 129는 125보다 큰 첫 번째 항입니다.

답) 129

284

문제) 다음의 값을 구하세요: (4 5/8)⁵⁵ · (8/37)⁵⁵.

풀이) 먼저 4 5/8을 가분수로 변환합니다: 4 5/8 = 4 + 5/8 = 32/8 + 5/8 = 37/8. 4 5/8과 8/37은 서로 역수 관계에 있습니다. (ab)ⁿ = aⁿbⁿ이라는 사실을 사용하여, 다음과 같이 계산할 수 있습니다: (4 5/8)⁵⁵ · (8/37)⁵⁵ = (4 5/8 · 8/37)⁵⁵ = 1⁵⁵ = 1.

답) 1

285

문제) 다음 방정식의 모든 해를 구하세요: sin(tan^-1(x) + cot^-1(1/x)) = 1/3. 모든 해를 쉼표로 구분하여 입력하세요.

풀이) 모든 x에 대해 cot^-1(1/x) = tan^-1(x)이므로, sin(2 tan^-1(x)) = 1/3로 쓸 수 있습니다. θ = tan^-1(x)라고 하면, x = tan(θ)입니다. 또한, sin(2θ) = 1/3이므로, 2 sin(θ) cos(θ) = 1/3입니다. 다리의 길이가 1과 x인 직각삼각형을 구성합니다. 그러면 x의 길이에 대립하는 각이 θ가 됩니다. 아래는 도형을 그리는 코드입니다.

unitsize(1 cm);

pair A, B, C;

A = (2,1.8);
B = (0,0);
C = (2,0);

draw(A--B--C--cycle);
draw(rightanglemark(A,C,B,8));

label("$\theta$", B + (0.7,0.3));
label("$1$", (B + C)/2, S);
label("$x$", (A + C)/2, E);
label("$\sqrt{x^2 + 1}$", (A + B)/2, NW);

또한, 빗변은 √(x² + 1)이므로, cos(θ) = 1/√(x² + 1)이고 sin(θ) = x/√(x² + 1)입니다. 따라서, 2 · (1/√(x² + 1)) · (x/√(x² + 1)) = 1/3이 됩니다. 즉, 2x/(x² + 1) = 1/3입니다. 이를 통해 x² + 1 = 6x, 또는 x² - 6x + 1 = 0이 됩니다. 이차 방정식의 해는 x = 3 ± 2√2입니다.

답) 3 ± 2√2

286

문제) 스티브가 존에게 말한다.

“나는 모든 근이 양의 정수인 어떤 다항식을 생각하고 있어. 그 다항식은 P(x) = 2x³ − 2ax² + (a² − 81)x − c 꼴이고, a와 c는 양의 정수야. a와 c 값을 맞힐 수 있겠니?”

계산을 좀 해 본 존이 말한다.

“이 조건을 만족하는 다항식이 하나가 아니라 여러 개네요.”

스티브가 말한다.

“맞아. 여기 a 값이야.”

(양의 정수를 하나 적는다)

“이제 c 값을 말할 수 있겠니?”

존이 말한다.

“여전히 c 값이 두 가지 가능성이 있어요.”

가능한 두 c 값의 합을 구하여라.

풀이) P(x)의 세 양의 정수 근을 r, s, t라고 하자. 비에타 정리에 의해 다음이 성립한다.

1) r + s + t = a

2) rs + st + rt = (a² − 81)/2

3) rst = c/2

1)을 2)에 대입하여 a를 없애면, rs + st + rt = ((r + s + t)² − 81)/2 = ((r² + s² + t²) + 2(rs + st + rt) − 81)/2. 이를 정리하면 r² + s² + t² = 81 이므로 r, s, t는 모두 1부터 9까지의 정수 중 하나이다. 또 r ≤ s ≤ t라고 두면, 81 = r² + s² + t² ≤ 3t² 이므로 t² ≥ 27, 따라서 t ≥ 6이다. 이제 t 값에 따라 경우를 나눈다.

t = 6이면 r² + s² = 81 − 6² = 45 r ≤ s ≤ 6을 만족하는 해는 (r, s) = (3, 6)뿐이다. t = 7이면 r² + s² = 81 − 7² = 32 r ≤ s ≤ 7을 만족하는 해는 (r, s) = (4, 4)뿐이다. t = 8이면 r² + s² = 81 − 8² = 17 r ≤ s ≤ 8을 만족하는 해는 (r, s) = (1, 4)뿐이다. 따라서 가능한 근의 집합은 (3, 6, 6), (4, 4, 7), (1, 4, 8) 이다.

각 경우에 대해 a = r + s + t, c = 2rst를 계산하면

(3, 6, 6) → a = 15, c = 216

(4, 4, 7) → a = 15, c = 224

(1, 4, 8) → a = 13, c = 64

문제에서 “a를 알려줘도 c가 두 가지로 남는다”고 했으므로, 같은 a에 대해 c가 두 개 나오는 경우여야 한다. a = 15일 때는 c가 216 또는 224로 두 가지가 가능하지만, a = 13일 때는 c가 64 하나뿐이다. 따라서 a = 15이고, 가능한 두 c의 합은 216 + 224 = 440 이다.

답) 440

287

문제) 양의 정수 a, b, c로 이루어진 모든 삼중쌍 (a,b,c)의 집합 T가 삼각형의 변의 길이로 존재한다고 하자. 다음을 계산하시오. ∑_{(a,b,c) ∈ T} (2ᵃ / (3ᵇ 5ᶜ)).

풀이) 변의 길이가 a, b, c인 삼각형에 대해 s = (a + b + c) / 2라고 하고, x = s - a = (-a + b + c) / 2, y = s - b = (a - b + c) / 2, z = s - c = (a + b - c) / 2. 삼각형 부등식에 의해 x, y, z는 모두 양수입니다. (이 기법은 종종 Ravi 대체법이라고 불립니다.) a = y + z, b = x + z, c = x + y. s가 짝수라면, x, y, z는 모두 양의 정수입니다. 따라서 x = i, y = j, z = k로 설정할 수 있으며, 이는 (a,b,c) = (j + k, i + k, i + j)의 매개변수를 제공합니다. s가 홀수라면, x, y, z는 모두 n - 1/2의 형태로, 여기서 n은 양의 정수입니다. 따라서 x = i - 1/2, y = j - 1/2, z = k - 1/2로 설정할 수 있으며, 이는 (a,b,c) = (j + k - 1, i + k - 1, i + j - 1)의 매개변수를 제공합니다. 따라서, 우리의 합은 다음과 같습니다. ∑_{i=1 to ∞} ∑_{j=1 to ∞} ∑_{k=1 to ∞} (2ʲ⁺ᵏ / (3ᶦ⁺ᵏ 5ᶦ⁺ʲ) + 2ʲ⁺ᵏ⁻¹ / (3ᶦ⁺ᵏ⁻¹ 5ᶦ⁺ʲ⁻¹)) = ∑_{i=1 to ∞} ∑_{j=1 to ∞} ∑_{k=1 to ∞} (2ʲ⁺ᵏ / (3ᶦ⁺ᵏ 5ᶦ⁺ʲ) + (15/2) · 2ʲ⁺ᵏ / (3ᶦ⁺ᵏ 5ᶦ⁺ʲ)) = 17/2 ∑_{i=1 to ∞} ∑_{j=1 to ∞} ∑_{k=1 to ∞} (2ʲ⁺ᵏ / (3ᶦ⁺ᵏ 5ᶦ⁺ʲ)) = 17/2 ∑_{i=1 to ∞} (1 / 15ᶦ) ∑_{j=1 to ∞} ((2/5)ʲ) ∑_{k=1 to ∞} ((2/3)ᵏ) = (17/2) · (1/15) / (1 - 1/15) · (2/5) / (1 - 2/5) · (2/3) / (1 - 2/3) = 17/21.

답) 17 / 21

288

문제) 하나의 기어는 1분에 33과 1/3번 회전합니다. 다른 기어는 1분에 45번 회전합니다. 처음에 각 기어의 표시가 북쪽을 가리키고 있습니다. 두 기어의 표시가 다시 북쪽을 가리키는 데 몇 초가 걸릴까요?

풀이) 하나의 기어는 60초 동안 33과 1/3 = 100/3번 회전하므로, 1초에 5/9번 회전하거나 9초에 5번 회전합니다. 다른 기어는 60초 동안 45번 회전하므로, 1초에 3/4번 회전하거나 4초에 3번 회전합니다. 두 기어의 표시가 다시 북쪽을 가리키는 시간을 찾기 위해 4 = 2²와 9 = 3²의 최소공배수를 찾아야 합니다. 최소공배수는 2² · 3² = 36입니다. 따라서 두 기어의 표시가 다시 북쪽을 가리키는 데 36초가 걸립니다. (하나의 기어는 정확히 5 × 4 = 20번 회전하고, 다른 기어는 정확히 3 × 9 = 27번 회전합니다.)

답) 36

289

문제) 한 직선은 다음과 같이 정의됩니다: (3, -10, 1) + t (2, -9, -2). 다른 직선은 다음과 같이 정의됩니다: (-5, -3, 6) + u (4, -18, -4). 이 두 직선은 평행합니다. 이 두 직선 사이의 거리를 구하세요.

풀이) 첫 번째 직선 위의 한 점은 (3, -10, 1)입니다. 두 번째 직선 위의 한 점은 다음과 같이 주어집니다: (x, y, z) = (-5, -3, 6) + t (4, -18, -4) = (-5 + 4t, -3 - 18t, 6 - 4t). 아래는 도형을 그리는 코드입니다.

unitsize (0.6 cm);

pair A, B, C, D, E, F, H;

A = (2,5);
B = (0,0);
C = (8,0);
D = (A + reflect(B,C)*(A))/2;

draw(A--D);
draw((0,5)--(8,5));
draw((0,0)--(8,0));

dot("$(3,-10,1)$", A, N);
dot("$(-5 + 4t, -3 - 18t, 6 - 4t)$", D, S);

(3, -10, 1)에서 (-5 + 4t, -3 - 18t, 6 - 4t)로 향하는 벡터는 v = (-8 + 4t, 7 - 18t, 5 - 4t)입니다. 두 번째 직선의 방향 벡터 (4, -18, -4)와 이 벡터가 직교할 때, 이 점은 (3, -10, 1)에 가장 가깝습니다. 따라서, (-8 + 4t, 7 - 18t, 5 - 4t) · (4, -18, -4) = 0입니다. 이를 풀면, t = 1/2가 됩니다. 이 값을 v에 대입하면, 평행한 두 직선 사이의 거리는 ||v|| = ||(-6, -2, 3)|| = 7입니다.

답) 7

290

문제) 양의 실수인 a, b, c, d가 주어졌을 때, 다음 식의 최소값을 구하세요. (a + b + c + d) (1/a + 1/b + 1/c + 1/d)

풀이) AM-GM 부등식에 의해, a + b + c + d ≥ 4√[4]{abcd}, 그리고 1/a + 1/b + 1/c + 1/d ≥ 4√[4]{1/abcd}, 따라서 (a + b + c + d) (1/a + 1/b + 1/c + 1/d) ≥ 4√[4]{abcd} · 4√[4]{1/abcd} = 16. 평등은 a = b = c = d일 때 성립하므로, 최소값은 16입니다.

답) 16

291

문제) r의 값을 구하세요. (6r² - 19r - 7) / (2r - 7) = 4r - 3.

풀이) 왼쪽의 이차식을 인수분해하면 (2r - 7)(3r + 1) / (2r - 7) = 4r - 3이 됩니다. 왼쪽의 공통 인수를 약분하면 3r + 1 = 4r - 3이 됩니다. 이 방정식을 풀면 r = 4입니다.

답) 4

292

문제) 다음 점들을 꼭짓점으로 하는 직사각형 영역을 고려하세요: (5,4), (-5,4), (-5,-4), (5,-4). 이 직사각형 영역의 내부에 엄격히 포함되는 정수 좌표를 가진 점은 몇 개입니까?

풀이) 직사각형 영역은 10 단위 x 8 단위로, 내부에는 8 x 6 직사각형 영역이 형성되며, 이는 9 x 7 격자의 격자점을 형성합니다. 따라서 정수 좌표를 가진 점은 총 63개입니다. 아래는 도형을 그리는 코드입니다.

import olympiad; size(150); defaultpen(linewidth(0.8));
add(grid(10,8));
draw((1,1)--(9,1)--(9,7)--(1,7)--cycle,linewidth(1.2));

참고: 우리는 점을 세고 있으며, 사각형을 세는 것이 아닙니다. 내부 사각형을 세어 48로 잘못 계산하는 대신, 내부 격자점을 세어 올바른 답인 63을 얻습니다.

답) 63

293

문제) 다음이 주어졌을 때, x₁ = 211, x₂ = 375, x₃ = 420, x₄ = 523, 그리고 n ≥ 5일 때, xₙ = xₙ₋₁ - xₙ₋₂ + xₙ₋₃ - xₙ₋₄ 가 성립합니다. 이때 x₅₃₁ + x₇₅₃ + x₉₇₅의 값을 구하세요.

풀이) 재귀식을 하나씩 이동시키고 더하면, xₙ = xₙ₋₁ - xₙ₋₂ + xₙ₋₃ - xₙ₋₄이고 xₙ₋₁ = xₙ₋₂ - xₙ₋₃ + xₙ₋₄ - xₙ₋₅입니다. 따라서 xₙ + xₙ₋₁ = xₙ₋₁ - xₙ₋₅이므로, xₙ = -xₙ₋₅입니다. 특히, xₙ = -xₙ₋₅ = -(-xₙ₋₁₀) = xₙ₋₁₀이므로, 이 수열은 주기가 10입니다. 따라서, x₅₃₁ + x₇₅₃ + x₉₇₅ = x₁ + x₃ + x₅ = x₁ + x₃ + (x₄ - x₃ + x₂ - x₁) = x₂ + x₄ = 375 + 523 = 898입니다.

답) 898

294

문제) 다음 부등식을 모두 만족하는 p를 찾으세요: 0 ≥ 54p - 144 그리고 0 > 12 - 20p. 답을 구간 표기법으로 표현하고, 분수를 가능한 한 간단히 하세요.

풀이) 각각의 부등식을 하나씩 해결해 봅시다. 첫 번째 부등식에 양변에 144를 더하면, 144 ≥ 54p가 됩니다. 이는 144 / 54 ≥ p를 의미합니다. 분수를 간단히 하고 부등식의 방향을 바꾸면, p ≤ 8 / 3이 됩니다. 두 번째 부등식을 해결하기 위해, 양변에 20p를 더하면 20p > 12가 됩니다. 양변을 20으로 나누면, p > 12 / 20이 됩니다. 분수를 간단히 하면 p > 3 / 5가 됩니다. 두 부등식을 모두 만족하는 p를 찾기 위해, 위의 해의 교집합을 구하면 (3 / 5, 8 / 3]이 됩니다.

답) (3 / 5, 8 / 3]

295

문제) 회문수는 앞에서 읽으나 뒤에서 읽으나 같은 숫자입니다. 세 개의 연속된 양의 정수 집합의 합이 세 자리 회문수입니다. 합이 220보다 작다면, 집합에서 가장 큰 정수의 가능한 최대값은 무엇입니까?

풀이) 세 개의 연속된 정수 집합 {n-1, n, n+1}의 합은 3n입니다. 따라서 우리는 220보다 작은 세 자리 회문수 중 3의 배수인 가장 큰 수를 찾고자 합니다. 212, 202, 191, 181, 171을 확인한 결과, 171이 3의 배수인 가장 큰 회문수입니다. 3n = 171을 풀면 n = 57이 됩니다. 세 정수는 56, 57, 58이며, 가장 큰 수는 58입니다.

답) 58

296

문제) 방정식 z⁴ + 4z³i - 6z² - 4zi - i = 0의 해는 복소평면에서 볼록 다각형의 꼭짓점입니다. 이 다각형의 면적은 p^a/b 형태로 표현될 수 있으며, 여기서 a, b, p는 양의 정수이고, p는 소수이며, a와 b는 서로소입니다. a + b + p를 구하세요.

풀이) 이항 정리에 의해, (z + i)⁴ = z⁴ + 4z³i + 6z² i² + 4zi³ + 1 = z⁴ + 4iz³ - 6z² - 4iz + 1. 따라서, z⁴ + 4z³i - 6z² - 4zi - i = 0이라면, (z + i)⁴ = z⁴ + 4iz³ - 6z² - 4iz + 1 = 1 + i. w = z + i라고 하면, w⁴ = 1 + i입니다. (복소평면에서 w의 해를 그리면, w = z + i 대입은 단순히 다각형을 평행 이동시키므로 z의 해와 동일한 면적을 얻습니다.) w⁴ = 1 + i라면, (wi)⁴ = w⁴i⁴ = w⁴ = 1 + i입니다. 따라서, w가 해라면 iw, i²w = -w, i³w = -iw도 해가 되며, 이는 복소평면에서 정사각형을 형성합니다. 아래는 도형을 그리는 코드입니다.

unitsize(2 cm);

pair A, B, C, D;

A = 2^(1/8)*dir(45/4);
B = 2^(1/8)*dir(45/4 + 90);
C = 2^(1/8)*dir(45/4 + 180);
D = 2^(1/8)*dir(45/4 + 270);

draw(A--B--C--D--cycle);
draw((-1.5,0)--(1.5,0));
draw((0,-1.5)--(0,1.5));

dot("$w$", A, E);
dot("$iw$", B, N);
dot("$-w$", C, W);
dot("$-iw$", D, S);

방정식 w⁴ = 1 + i에서, |w⁴| = |1 + i|입니다. 그러면 |w|⁴ = √2이므로, |w| = 2^1/8입니다. 따라서 정사각형의 변의 길이는 |w - iw| = |w||1 - i| = 2^1/8√2 = 2^5/8이므로, 정사각형의 면적은 (2^5/8)² = 2^5/4입니다. 최종 답은 5 + 4 + 2 = 11입니다.

답) 11

297

문제) 0

(A) 3(1 + r)ˣ = 7

(B) 3(1 + r/10)ˣ = 7

(D) 3(1 + √(r))ˣ = 7

(E) 3(1 + 1/r)ˣ = 7

풀이) 직관적으로, 괄호 안의 값이 가장 작은 경우 x가 가장 큽니다. 공식적으로, 먼저 괄호 안의 각 값이 1보다 크다는 것을 주목합니다. 이제 각 옵션은 3f(r)ˣ = 7의 형태입니다. 이는 x log f(r) = log(7/3)로 다시 쓸 수 있습니다. f(r) > 1이므로 log f(r) > 0입니다. 따라서 x는 log f(r)이 가장 작은 옵션에서 가장 큽니다. log f(r)은 증가 함수이므로, 이는 f(r)이 가장 작은 옵션입니다. 이제 더 쉬운 문제로 바뀝니다: 0 (B) 3(1 + r/10)ˣ = 7입니다.

답) (B)

298

문제) 책이 n 장의 종이로 구성되어 있으면 n 장의 잎을 가지고 있다고 합니다. 한편, 종이의 각 면은 페이지로 정의되므로 페이지 수는 잎 수의 두 배입니다. 책의 페이지 수가 7의 배수보다 3이 더 많고, 잎 수가 100보다 크다면, 가능한 가장 작은 잎 수는 얼마입니까?

풀이) 가장 작은 잎 수를 m이라고 합시다. 그러면 2m은 가장 작은 페이지 수입니다. 우리는 2m equiv 3 pmod{7}임을 알고 있습니다. 이는 8m equiv 3 · 4 pmod{7}을 의미하며, 따라서 m equiv 12 equiv 5 pmod{7}입니다. 따라서 m = 5 + 7a (어떤 양의 정수 a)입니다. 100보다 큰 가장 작은 수는 5 + 7 · 14 = 103입니다.

답) 103

299

문제) 벡터 a, b, c 가 다음과 같다고 하자: a × b = (6, -7, 3), a × c = (4, 7, 2), b × c = (1, -7, 18). (2b - a) × (3c + a) 를 계산하시오.

풀이) 전개하면, (2b - a) × (3c + a) = 6b × c + 2b × a - 3a × c - a × a = 6b × c - 2a × b - 3a × c - 0 = 6 (1, -7, 18) - 2 (6, -7, 3) - 3 (4, 7, 2) = (-18, -49, 96).

답) (-18, -49, 96)

300

문제) 꼭짓점이 (5, 4), (5, -4), (-5, 4), (-5, -4)에 있는 직사각형을 고려하세요. 직사각형 내부에 엄격히 포함되는 정수 좌표는 몇 개입니까?

풀이) 정수 좌표를 갖는 점을 격자점이라고 합니다. 직사각형의 길이는 5 - (-5) = 10 단위입니다. 직사각형의 두 수직 변 사이에는 9개의 격자 위치가 있습니다. 직사각형의 높이는 4 - (-4) = 8 단위입니다. 직사각형의 위쪽과 아래쪽 사이에는 7개의 격자 위치가 있습니다. 따라서 총 9 × 7 = 63개의 격자점이 있습니다.

답) 63

301

문제) 평면에 네 개의 서로 다른 원이 그려져 있습니다. 적어도 두 개의 원이 교차하는 점의 최대 개수는 얼마입니까?

풀이) 각 원의 쌍은 최대 두 개의 교차점을 가질 수 있습니다. 원의 쌍은 총 4개 중 2개를 선택하는 경우의 수로, 6쌍이 있습니다. 따라서 최대 6 × 2 = 12개의 교차점이 있을 수 있습니다. 다음 구성은 12개의 교차점이 실제로 가능함을 보여줍니다: 아래는 도형을 그리는 코드입니다.

draw(Circle((0,0),2));
draw(Circle((1,1.3),2));
draw(Circle((-1,1.3),2));
draw(Circle((0,0.7),2));

답) 12

302

문제) 후안의 오래된 우표 수집 후안은 자신의 우표 수집품을 국가별로, 그리고 발행된 10년 단위로 정리합니다. 그가 우표 가게에서 지불한 가격은 다음과 같습니다: 브라질과 프랑스는 각각 6센트, 페루는 4센트, 스페인은 5센트입니다. (브라질과 페루는 남미 국가이고 프랑스와 스페인은 유럽에 있습니다.) 아래는 도형을 그리는 코드입니다.

/* AMC8 2002 #8, 9, 10 Problem */
size(3inch, 1.5inch);
for ( int y = 0; y <= 5; ++y ){
 draw((0,y)--(18,y));
}
draw((0,0)--(0,5));
draw((6,0)--(6,5));
draw((9,0)--(9,5));
draw((12,0)--(12,5));
draw((15,0)--(15,5));
draw((18,0)--(18,5));

label(scale(0.8)*"50s", (7.5,4.5));
label(scale(0.8)*"4", (7.5,3.5));
label(scale(0.8)*"8", (7.5,2.5));
label(scale(0.8)*"6", (7.5,1.5));
label(scale(0.8)*"3", (7.5,0.5));

label(scale(0.8)*"60s", (10.5,4.5));
label(scale(0.8)*"7", (10.5,3.5));
label(scale(0.8)*"4", (10.5,2.5));
label(scale(0.8)*"4", (10.5,1.5));
label(scale(0.8)*"9", (10.5,0.5));

label(scale(0.8)*"70s", (13.5,4.5));
label(scale(0.8)*"12", (13.5,3.5));
label(scale(0.8)*"12", (13.5,2.5));
label(scale(0.8)*"6", (13.5,1.5));
label(scale(0.8)*"13", (13.5,0.5));

label(scale(0.8)*"80s", (16.5,4.5));
label(scale(0.8)*"8", (16.5,3.5));
label(scale(0.8)*"15", (16.5,2.5));
label(scale(0.8)*"10", (16.5,1.5));
label(scale(0.8)*"9", (16.5,0.5));

label(scale(0.8)*"Country", (3,4.5));
label(scale(0.8)*"Brazil", (3,3.5));
label(scale(0.8)*"France", (3,2.5));
label(scale(0.8)*"Peru", (3,1.5));
label(scale(0.8)*"Spain", (3,0.5));

label(scale(0.9)*"Juan's Stamp Collection", (9,0), S);
label(scale(0.9)*"Number of Stamps by Decade", (9,5), N);

그의 70년대 우표의 평균 가격은 얼마였습니까? 답을 소수점 첫째 자리까지 반올림하세요.

풀이) 70년대 우표의 비용은 다음과 같습니다: • 브라질, 12 × 0.06달러 = 0.72달러; • 페루, 6 × 0.04달러 = 0.24달러; • 프랑스, 12 × 0.06달러 = 0.72달러; • 스페인, 13 × 0.05달러 = 0.65달러. 총합은 2.33달러이고, 43개의 우표에 대한 평균 가격은 2.33달러 / 43 ≈ 0.054달러 = 5.4센트입니다.

답) 5.4센트

303

문제) 분수 31 / 11111을 소수로 변환할 때, 이 소수는 순환소수가 됩니다. 이 순환소수에서 몇 자리 숫자가 반복되는지 구하세요. 예를 들어, 순환소수가 0.123이라면, 답은 3이 되어야 하고, 0.4367이라면, 답은 1이 되어야 합니다.

풀이) 우선, 31 / 11111 = (31 × 9) / (11111 × 9) = 279 / 99999임을 알 수 있습니다. 우리는 279 / 99999 = 0.00279임을 보일 것입니다. 따라서 최종 답은 5입니다. 279 / 99999 = 0.00279임을 증명합니다: s = 0.00279라고 합시다. 그러면 양변에 10⁵를 곱하면 10⁵ s = 279.00279가 됩니다. 양변에서 s와 0.00279를 각각 빼면 99999s = 279가 되어, s = 279 / 99999가 됩니다. 따라서 0.00279 = 279 / 99999임을 알 수 있습니다.

답) 5

304

문제) 사다리꼴 ABCD에서 선분 AD || 선분 BC라고 가정합시다. 선분 AC ⊥ 선분 CD이고, 선분 AC가 ∠BAD를 이등분하며, [ABCD]=42일 때, [△ACD]를 구하세요.

풀이) 여러 가지 방법으로 도형을 그릴 수 있습니다. 한 가지 가능성은 아래에 표시되어 있습니다. 선분 AC이 ∠BAD를 이등분하고 선분 AD || 선분 BC이므로 ∠BAC ≃ ∠CAD ≃ ∠BCA입니다. 따라서 △BAC는 이등변 삼각형입니다. 도형에 선분 BE를 추가하여 △BAC를 두 개의 작은 합동 직각삼각형으로 나누었습니다. 또한, 주어진 조건에 의해 △ACD는 직각삼각형이므로 △ACD ∼ △CEB입니다. 실제로 △ACD는 △CEB의 정확히 네 배 크기입니다. 왜냐하면 AC=2(EC)이기 때문입니다. [△CEB] = K라고 하면, [△AEB]=K이고 [△ACD]=4K입니다. 따라서 6K=42이므로 K=7이고 [△ACD]=4K=28입니다. 아래는 도형을 그리는 코드입니다.

import olympiad; import graph; size(150); defaultpen(linewidth(0.8)); dotfactor=4;
int randangle = 50;
draw((-5,0)--(5*dir(randangle))--(5,0)--cycle);
path x1 = (5*Cos(randangle),5*Sin(randangle))--(-10,5*Sin(randangle));
path x2 = (-5,0)--(5dir(2*randangle));
pair X = intersectionpoint(x1,x2);
draw((-5,0)--X--(5*dir(randangle)));
draw(rightanglemark((5,0),(5*dir(50)),(-5,0),s=14));
draw(anglemark((5,0),(-5,0),X,18));
draw(anglemark(X,5*dir(50),(-5,0),18));
label("$A$",(-5,0),W); label("$D$",(5,0),E); label("$C$",(5*dir(50)),E);
label("$B$",(X),N);

pair l = foot(X,(-5,0),5*dir(50));
draw(X--l);
draw(rightanglemark(X,l,(-5,0),14)); draw(rightanglemark(X,l,(5*dir(50)),14));
label("$E$",l,SE);

답) 28

305

문제) 다음 식의 최소값을 구하세요: (x + 5)(x + 2) / x + 1 단, x > 0.

풀이) 전개하면, (x + 5)(x + 2) / x + 1 = x² + 7x + 10 / x + 1. 나눗셈을 통해, x² + 7x + 10 / x + 1 = x + 6 + 4 / x + 1 = (x + 1) + 4 / x + 1 + 5. 산술-기하 평균 부등식(AM-GM)에 의해, (x + 1) + 4 / x + 1 ≥ 2 sqrt{(x + 1) · 4 / x + 1} = 4, 따라서 (x + 1) + 4 / x + 1 + 5 ≥ 9. 평등은 x = 1일 때 성립하므로, 최소값은 9입니다.

답) 9

306

문제) 만약 √(2x) / √(3x-1) = 3 / 2 라면, x 를 구하세요. 답을 가장 간단한 분수 형태로 표현하세요.

풀이) 우선 교차 곱셈을 합니다: 3√(3x-1) = 2√(2x) ⇒ (3√(3x-1))² = (2√(2x))² ⇒ 9(3x-1) = 4(2x) ⇒ 27x - 9 = 8x ⇒ 19x = 9 ⇒ x = 9 / 19. 확인해보면, 이 값의 x 는 실제로 성립하므로, 이는 허수 해가 아닙니다.

답) 9 / 19

307

문제) 방정식 x² + ax + b = 0의 근이 c일 때, c² - 2도 방정식의 근이 되는 이차 방정식의 개수를 구하시오.

풀이) 근이 r와 s라고 하자 (반드시 실수일 필요는 없음). 우리는 r = s인 경우와 r ≠ s인 경우를 고려합니다.

경우 1: r = s인 경우. r이 유일한 근이므로 r² - 2 = r이어야 합니다. 그러면 r² - r - 2 = 0이 되고, 이는 (r - 2)(r + 1) = 0으로 인수분해됩니다. 따라서 r = 2 또는 r = -1입니다. 이는 이차 방정식 x² - 4x + 4와 x² + 2x + 1을 유도합니다.

경우 2: r ≠ s인 경우. r² - 2와 s² - 2 각각이 r 또는 s와 같아야 합니다. 우리는 세 가지 경우를 고려합니다:

(i) r² - 2 = r이고 s² - 2 = s인 경우.

(ii) r² - 2 = s이고 s² - 2 = r인 경우.

(iii) r² - 2 = s² - 2 = r인 경우.

경우 (i)에서, 경우 1에서 본 것처럼 r, s in {2,-1}입니다. 이는 이차 방정식 (x - 2)(x + 1) = x² - x - 2를 유도합니다.

경우 (ii)에서, r² - 2 = s이고 s² - 2 = r입니다. 이 방정식을 빼면 (r - s)(r + s) = s - r이 됩니다. r - s ≠ 0이므로, 양변을 r - s로 나누면 r + s = -1이 됩니다. 방정식 r² - 2 = s와 s² - 2 = r을 더하면 r² + s² - 4 = r + s = -1이므로 r² + s² = 3입니다. r + s = -1을 제곱하면 r² + 2rs + s² = 1이므로 2rs = -2, 즉 rs = -1입니다. 따라서 r과 s는 x² + x - 1의 근입니다.

경우 (iii)에서, r² - 2 = s² - 2 = r입니다. 그러면 r² - r - 2 = 0이므로 r = 2 또는 r = -1입니다. 만약 r = 2라면, s² = 4이므로 s = -2입니다. (우리는 r ≠ s를 가정하고 있습니다.) 이는 이차 방정식 (x - 2)(x + 2) = x² - 4를 유도합니다. 만약 r = -1이라면, s² = 1이므로 s = 1입니다. 이는 이차 방정식 (x + 1)(x - 1) = x² - 1을 유도합니다.

따라서 조건을 만족하는 이차 방정식은 총 6개, 즉 x² - 4x + 4, x² + 2x + 1, x² - x - 2, x² + x - 1, x² - 4, x² - 1입니다.

답) 6

308

문제) 함수 y = log₂(√(sin x))의 범위는 무엇입니까? (0° < x < 180°)

풀이) 0도에서 180도 사이에서, sin x의 값은 0 (포함하지 않음)에서 1 (포함) 사이입니다. 따라서, √(sin x)의 값은 0 (포함하지 않음)에서 1 (포함) 사이입니다. log₂ x의 범위는 0 < x ≤ 1일 때 모든 음수가 포함되므로, 전체 함수의 범위는 모든 음수, 즉 x ∈ (-∞, 0]입니다.

답) (-∞, 0]

309

문제) 정사면체 ABCD의 변의 길이가 2라고 하자. AB와 CD에 평행하고 그 사이의 중간에 위치한 평면이 ABCD를 두 조각으로 나눈다. 이 조각 중 하나의 표면적을 구하시오.

풀이) 평면은 정사면체의 각 면을 중간선에서 교차하며, 대칭에 의해 평면과 정사면체의 교차는 한 변의 길이가 1인 정사각형이 된다. 각 조각의 표면적은 정사면체의 총 표면적의 절반에 정사각형의 면적을 더한 것이며, 이는 1/2 × 4 × (2²√3 / 4) + 1 = 1 + 2√3이다.

답) 1 + 2√3

310

문제) 서로 다른 양의 정수 집합의 곱이 84입니다. 이 정수들의 합이 최소가 되도록 하려면 어떻게 해야 할까요?

풀이) 84의 소인수는 2² · 3 · 7입니다. 합이 가장 작은 집합은 이 소인수들 자체일 것입니다: 2, 2, 3, 7. 하지만 정수들이 서로 달라야 하므로 두 개의 2를 가질 수 없습니다. 대신 4, 3, 7을 가질 수 있습니다. 이 숫자들의 합은 14입니다. 또한, 하나의 2를 3과 짝지어 2, 6, 7로 만들 수도 있지만, 이 경우 합은 15가 됩니다. 추가적인 2를 7과 짝지어 2, 3, 14로 만들면 합이 19가 되며, 다른 조합은 명백히 14보다 큰 합을 줍니다.

답) 14

311

문제) 연산 @는 다음과 같이 정의됩니다: m/n @ p/q = (m)(p)(q/n) 여기서 p/q는 기약 분수입니다. 그렇다면 7/30 @ 10/21의 기약값은 무엇입니까?

풀이) 7/30 @ 10/21 = (7)(10)(21/30) = 49입니다.

답) 49

312

문제) 만약 1 + 12 + 123 + 1234 + 12345 + 123456 + 1234567 + 12345678이 9로 나눈 나머지가 n이라면, 여기서 0 ≤ n < 9일 때, n의 값은 얼마입니까?

풀이) 어떤 수는 그 수의 각 자리 숫자의 합과 9로 나눈 나머지가 같습니다. 따라서, 1 + 12 + 123 + 1234 + 12345 + 123456 + 1234567 + 12345678 ≡ 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 (mod 9) ≡ 1 + 3 + 6 + 1 + 6 + 3 + 1 + 9 (mod 9) ≡ 30 (mod 9) ≡ 3 (mod 9).

답) 3

313

문제) 다음을 풀어라 1 / (x - 5) > 0. 답을 구간 표기법으로 입력하세요.

풀이) x 5이면 1 / (x - 5) > 0이므로, 해는 x ∈ (5, ∞)입니다.

답) (5, ∞)

314

문제) 찰리는 외발자전거를 타고 있습니다. 외발자전거의 바퀴 반지름이 9인치이고, 3초마다 2회전 한다면, 외발자전거의 속도는 초당 몇 인치입니까?

풀이) 외발자전거 바퀴의 한 바퀴에 몇 인치가 있는지 알아야 합니다. 즉, 바퀴의 둘레를 알아야 합니다. 반지름이 9인치이므로, 둘레는 18π 인치입니다. 따라서 한 바퀴에 18π 인치가 있고, 바퀴가 3초마다 2회전 한다면, 외발자전거의 속도는 18π · (2 / 3) = 12π 인치/초입니다.

답) 12π

315

문제) 점 (0,0)을 수직선 x=1에 대해 반사시킵니다. 그 이미지가 다시 직선 y=2에 대해 반사될 때, 결과 점은 무엇입니까? 답을 (x, y) 형태로 작성하세요. 여기서 x와 y는 실수입니다.

풀이) 점 (0,0)을 직선 x=1에 대해 반사시키면, 이미지는 (2,0)이 됩니다. 아래는 도형을 그리는 코드입니다.

draw((-2, 0)--(6, 0), Arrow); draw((0, -2)--(0, 6), Arrow);
label("$x$", (6, 0), E); label("$y$", (0, 6), N);
label("$(0, 0)$", (0, 0), SW); label("$(2, 0)$", (2, 0), SE);
label("$(2, 4)$", (2, 4), NE);
label("$y = 2$", (6, 2), E); label("$x = 1$", (1, -2), S);
draw((-2, 2)--(6, 2), dashed); draw((1, -2)--(1, 6), dashed);
dot((0, 0)); dot((2, 0)); dot((2, 4));

점 (2,0)을 직선 y=2에 대해 반사시키면, 이미지는 (2,4)가 됩니다.

답) (2,4)

316

문제) 양의 정수 a, b, 2009가 있으며, a < b < 2009이고, 이들은 정수 비율을 갖는 등비수열을 이룹니다. a는 무엇입니까?

풀이) 2009의 소인수 분해는 2009 = 7 · 7 · 41입니다. a < b < 2009이므로, 비율은 양수이고 1보다 커야 합니다. 따라서 가능한 비율은 하나뿐입니다: 비율은 7이어야 하며, 따라서 b = 7 · 41이고 a = 41입니다.

답) 41

317

문제) 다항식 10x² - x - 24는 (Ax - 8)(Bx + 3) 형태로 표현될 수 있으며, 여기서 A와 B는 정수입니다. AB + B의 값을 구하세요.

풀이) 10x² - x - 24 = (5x - 8)(2x + 3)임을 알 수 있습니다. 따라서 A = 5이고 B = 2입니다. 그러므로 AB + B = 12입니다.

답) 12

318

문제) 서로 다른 실수인 a, b, c가 주어졌을 때, 다음 다항식 p(x)의 차수를 구하세요. p(x) = ((x - b)(x - c)) / ((a - b)(a - c)) + ((x - a)(x - c)) / ((b - a)(b - c)) + ((x - a)(x - b)) / ((c - a)(c - b))

풀이) p(x)는 최대 차수가 2인 다항식입니다. 또한, p(a) = p(b) = p(c) = 1입니다. 따라서, 다항식 p(x)와 1은 세 가지 다른 값에서 일치하므로, 항등 정리에 의해 이들은 동일한 다항식입니다. 따라서, p(x)의 차수(상수 다항식 1)는 0입니다. 직접 확인해보면, p(x) = ((x - b)(x - c)) / ((a - b)(a - c)) + ((x - a)(x - c)) / ((b - a)(b - c)) + ((x - a)(x - b)) / ((c - a)(c - b)) 는 1로 단순화됩니다.

답) 0

319

문제) 다음 식 4+6a / 5-1+3a / 4 을 하나의 분수로 나타내세요.

풀이) 5와 4의 공통 분모는 20이므로, 첫 번째 분수의 분자와 분모에 4를 곱하고 두 번째 분수의 분자와 분모에 5를 곱합니다. 그러면 다음과 같이 됩니다: 4(4+6a) / 4 · 5 - 5(1+3a) / 4 · 5 = 16+24a / 20-5+15a / 20. 분수를 결합할 때, 두 번째 분수의 분자를 괄호로 묶어 전체 분자를 빼는 것에 주의하여 다음과 같이 계산합니다: 16+24a-(5+15a) / 20 = 16+24a-5-15a / 20=11+9a / 20.

답) 11 + 9a / 20

320

문제) 방정식 |x-4| - 10 = 2에서, 가능한 모든 x 값의 곱은 무엇입니까?

풀이) 주어진 방정식을 |x-4| = 12로 정리합니다. 따라서 x-4 = 12이면 x = 16이고, x-4 = -12이면 x = -8입니다. 따라서 답은 16 · (-8) = -128입니다.

답) -128

321

문제) 아래 그림에서, 우리는 sin ∠RPQ = 7 / 25 입니다. cos ∠RPS는 얼마입니까? 아래는 도형을 그리는 코드입니다.

pair R,P,Q,SS;
SS = (-2,0);
P = (0,0);
Q = (2,0);
R = rotate(aSin(7/25))*(1.5,0);
dot("$S$",SS,S);
dot("$Q$",Q,S);
dot("$R$",R,N);
dot("$P$",P,S);
draw(Q--SS);
draw(P--R);

풀이) 어떤 각도 x에 대해, cos(180° - x) = -cos x 이므로, cos ∠RPS = cos(180° - ∠RPQ) = -cos ∠RPQ 입니다. sin² ∠RPQ + cos² ∠RPQ = 1 이므로, cos² ∠RPQ = 1 - (7 / 25)² = 576 / 625 입니다. ∠RPQ가 예각이므로, cos ∠RPQ = 24 / 25 이고, 따라서 cos ∠RPS = -cos ∠RPQ = -24 / 25 입니다.

답) -24 / 25

322

문제) 로봇이 일정한 속도로 전진할 때 1킬로미터를 이동하는 데 2.5시간이 걸립니다. 같은 일정한 속도로 전진할 때, 로봇이 특정 복도의 길이를 이동하는 데 90초가 걸립니다. 복도는 몇 미터 길이입니까?

풀이) 2.5시간은 2.5 × 60 = 150분, 또는 150 × 60 = 9000초와 같습니다. 이는 로봇이 복도를 이동한 시간보다 100배 더 깁니다. 따라서 복도는 1/100 킬로미터, 즉 1000/100 = 10미터입니다.

답) 10

323

문제) 함수 f(x) = x - 3 와 q(x) = bx + 1 이 주어졌습니다. 만약 f(q(1)) = -3 이라면, b의 값은 무엇입니까?

풀이) q(1) = b · 1 + 1 = b + 1 이므로, f(q(1)) = f(b + 1) 입니다. 함수 f의 정의를 적용하면, f(q(1)) = f(b + 1) = (b + 1) - 3 = b - 2 입니다. 따라서, f(q(1)) = -3 이라는 식을 통해 b - 2 = -3 을 얻을 수 있으며, 따라서 b = -1 입니다.

답) -1

324

문제) 네 점 A, B, C, D가 원의 둘레 위에 무작위로 독립적으로 선택됩니다. 선분 AB와 CD가 교차할 확률은 얼마입니까?

풀이) 네 개의 무작위 점이 A, B, C, D로 라벨링되기 전의 상황을 고려해 봅시다. 일반적인 경우, 이 점들은 서로 다른 점으로, 볼록 사각형을 형성합니다. A가 라벨링되었다고 가정합시다. B가 A의 반대쪽 꼭짓점으로 라벨링되면, 선분 AB와 CD는 교차할 것입니다. 그렇지 않으면 교차하지 않습니다. B로 라벨링할 수 있는 점이 3개 있으므로, 이 선분들이 교차할 확률은 1/3입니다. 아래는 도형을 그리는 코드입니다.

draw((0,1)..(1,0)..(0,-1)..(-1,0)..cycle);
dot((0,1)); dot((-5/13,-12/13)); dot((-1,0)); dot((4/5,3/5));
label("$A$",(0,1),N); label("$B$",(-5/13,-12/13),SSW); label("$C$",(-1,0),W); label("$D$",(4/5,3/5),NE);
draw((0,1)--(-5/13,-12/13),green); draw((-1,0)--(4/5,3/5),green);
draw((0,1)--(4/5,3/5),blue); draw((-1,0)--(-5/13,-12/13),blue);
draw((0,1)--(-1,0),red); draw((-5/13,-12/13)--(4/5,3/5),red);

이 다이어그램에서, 녹색 선분은 AB와 CD가 교차하는 라벨링을 나타내고, 파란색과 빨간색 선분은 AB와 CD가 교차하지 않는 동일하게 가능한 라벨링을 나타냅니다.

답) 1/3

325

문제) 도형에서, 중심이 D인 두 개의 원이 각각 반지름이 1과 2입니다. 음영이 있는 영역의 총 면적은 큰 원의 면적의 5/12입니다. 작은 각도 ∠ADC의 크기는 몇 도입니까? 아래는 도형을 그리는 코드입니다.

size(4cm);
defaultpen(linewidth(0.75));
real adc = 100;
pair d = (0, 0); pair a = 2 * dir(100); pair c = (2, 0);
path inner = arc(d, a/2, c/2, CW);

path outer = arc(d, c, a, CCW);
guide region1 = (a--a/2)..inner..(c/2--c)..outer..cycle;
guide region2 = arc(d, a/2, c/2, CCW)..(c/2--d--a/2)..cycle;
fill(region1, gray(0.75));
fill(region2, gray(0.75));
draw(unitcircle); draw(scale(2) * unitcircle);
draw(a--d--c);
label("$A$", a, N); label("$C$", c, E); label("$D$", d, NE);

풀이) ∠ADC = x°라고 가정합시다. 그러면 내부 원의 비음영 부분의 면적은 내부 원의 총 면적의 x/360입니다. 즉, (x/360) (π(1²)) = (x/360) π입니다 (∠ADC가 최대 중심각 360°의 x/360이기 때문입니다). 따라서 내부 원의 음영 부분의 면적은 π - (x/360) π = (360 - x)π / 360 입니다. 외부 고리의 총 면적은 외부 원과 내부 원의 면적 차이로, π(2²) - π(1²) = 3π입니다. 외부 고리의 음영 부분은 이 총 면적의 x / 360이 됩니다. 따라서 외부 고리의 음영 부분은 3xπ / 360 입니다. 따라서 총 음영 면적 (5/3 π와 같아야 함)은 x에 대한 식으로 3xπ / 360 + (360 - x)π / 360 = (360 + 2x)π / 360 입니다. 따라서 (360 + 2x) / 360 = 5/3 = 600 / 360이므로, 360 + 2x = 600, 따라서 x = 120입니다.

답) 120

326

문제) 높이가 8cm이고 반지름이 3cm인 원기둥 모양의 비커가 있습니다. 반지름이 6cm인 구형 탱크를 채우기 위해 몇 개의 비커가 필요합니까?

풀이) 우선, 3차원 물체의 부피 공식을 기억해야 합니다. 반지름이 r이고 높이가 h인 원기둥의 부피는 r²hπ이고, 반지름이 r인 구의 부피는 (4/3)r³π입니다. 원기둥 모양의 비커는 높이가 8cm이고 반지름이 3cm이므로, 그 부피는 3²·8·π = 72π 세제곱 센티미터입니다. 구의 반지름이 6cm이므로, 그 부피는 (4/3)·6³π = 288π 세제곱 센티미터입니다. 구형 탱크를 채우기 위해 필요한 비커의 수는 탱크의 부피를 원기둥의 부피로 나눈 값입니다. 즉, 288π / 72π = 4입니다.

답) 4

327

문제) 다음을 평가하세요. sin(arcsin 0.4 + arcsin 0.5) · sin(arcsin 0.5 - arcsin 0.4).

풀이) 각도 덧셈 및 뺄셈 공식을 사용하면, sin(x + y) = sin x cos y + cos x sin y, sin(x - y) = sin x cos y - cos x sin y, 따라서 sin(x + y) sin(x - y) = (sin x cos y + cos x sin y)(sin x cos y - cos x sin y) = sin² x cos² y + sin x cos x sin y cos y - sin x cos x sin y cos y - cos² x sin² y = sin² x (1 - sin² y) - (1 - sin² x) sin² y = sin² x - sin² x sin² y - sin² y + sin² x sin² y = sin² x - sin² y. x = arcsin 0.5, y = arcsin 0.4로 설정하면, sin(arcsin 0.5 + arcsin 0.4) · sin(arcsin 0.5 - arcsin 0.4) = sin²(arcsin 0.5) - sin²(arcsin 0.4) = 0.5² - 0.4² = 0.09 = 9 / 100.

답) 9 / 100

328

문제) 3차 단항식 P(x)가 주어져 있습니다. P(x)를 (x - 1)(x - 4)로 나눌 때 나머지가 R(x)이고, (x - 2)(x - 3)로 나눌 때 나머지가 2R(x)라고 가정합니다. P(0) = 5일 때, P(5)의 값을 구하세요.

풀이) 먼저 P(x) = x³ + ax² + bx + 5라고 합시다. 나머지 R(x)는 최대 1차이므로 R(x) = cx + d라고 합시다. P(x)를 (x - 1)(x - 4)로 나눌 때, 몫은 x + p 형태입니다. 따라서 P(x) = (x + p)(x - 1)(x - 4) + R(x) = (x + p)(x - 1)(x - 4) + cx + d로 쓸 수 있습니다. x²의 계수를 비교하면 a = p - 5입니다. P(x)를 (x - 2)(x - 3)로 나눌 때, 몫은 x + q 형태입니다. 따라서 P(x) = (x + q)(x - 2)(x - 3) + 2R(x) = (x + q)(x - 2)(x - 3) + 2(cx + d)로 쓸 수 있습니다. x²의 계수를 비교하면 a = q - 5입니다. 따라서 p = q입니다. x의 계수를 두 식에서 비교하면 b = c - 5p + 4,b = 2c - 5p + 6. 이 두 식을 빼면 c + 2 = 0이므로 c = -2입니다. 첫 번째 식에서 상수항을 비교하면 5 = 4p + d입니다. 따라서 P(5) = (5 + p)(4)(1) - 10 + d = 10 + 4p + d = 15입니다.

답) 15

329

문제) 함수 f(x)=⎣(-5/8)ˣ⎦가 x가 [0, ∞) 범위에 있을 때 정의되어 있고, f(x)는 실수입니다. f(x)의 범위에 존재하는 서로 다른 값은 몇 개입니까?

풀이) -5/8은 음수이므로, f(x)는 x가 정수일 때만 정의되며, 양수와 음수 값을 번갈아 가집니다. 또한, |-5/8| < 1이므로, |f(x)|는 계속 감소하여 x가 증가함에 따라 0에 가까워집니다. 따라서, 가장 큰 양수 값은 x=0일 때 발생하며, 이때 ⎣(-5/8)⁰⎦=1입니다. 가장 큰 절대값을 가지는 음수 값은 다음 정수 값인 x=1일 때 발생하며, 이때 ⎣(-5/8)¹⎦=-1입니다. 이는 -1 ≤ f(x) ≤ 1임을 의미합니다. f(x)는 정수여야 하므로, 범위에 포함된 서로 다른 가능한 값은 -1, 0, 1입니다. 따라서 x≥0일 때 f(x)의 값은 총 3개입니다.

답) 3

330

문제) 자전거가 분당 20피트의 속도로 이동하고 있습니다. 자전거의 속도를 초당 인치로 표현하면 얼마입니까?

풀이) 1피트에는 12인치가 있으므로, 자전거는 분당 12 × 20 = 240인치의 속도로 이동하고 있습니다. 1분에는 60초가 있으므로, 자전거는 초당 240 / 60 = 4인치의 속도로 이동하고 있습니다.

답) 4

331

문제) 상원 위원회에는 8명의 공화당원과 6명의 민주당원이 있습니다. 각 당에서 적어도 한 명의 구성원이 포함된 5명의 소위원회를 구성하는 방법은 몇 가지입니까?

풀이) 제한 없이 5명의 소위원회를 선택하는 방법은 총 14명 중 5명을 선택하는 경우의 수로, 이는 14C5 = 2002가지입니다. 이 중에서 주어진 조건을 위반하는 경우는 모두 공화당원으로만 구성되거나 모두 민주당원으로만 구성된 경우입니다. 8명의 공화당원 중 5명을 선택하는 경우의 수는 8C5 = 56가지이고, 6명의 민주당원 중 5명을 선택하는 경우의 수는 6C5 = 6가지입니다. 조건에 맞지 않는 소위원회의 수를 전체 가능한 소위원회의 수에서 빼면 답을 얻을 수 있습니다: 2002 - 56 - 6 = 1940.

답) 1940

332

문제) 다음 식을 간단한 분수로 단순화하세요: √((5/√80 + √845/9 + √45) / √5).

풀이) 먼저, 큰 제곱근 안의 분수의 분자에 있는 각 항에 √5를 나눕니다: √((5/√80 + √845/9 + √45) / √5) = √(5/(√80·√5) + √845/(9√5) + √45/√5). 이제 제곱근 안의 각 분수를 따로 계산해 보겠습니다. 먼저, 5/(√80·√5) = 5/√400 = 5/20 = 1/4. 두 번째 항은 조금 더 복잡합니다: √845/(9√5) = √169/9 = 13/9. 마지막으로, √45/√5 = √9 = 3. 이들을 더하면, √(1/4 + 13/9 + 3) = √((9 + 52 + 108) / 36) = √(169/36) = 13/6.

답) 13/6

333

문제) 양의 실수인 x, y, z가 주어져 있고, xyz(x + y + z) = 1일 때, (x + y)(y + z)의 최소값을 구하시오.

풀이) (x + y)(y + z)를 xz + y(x + y + z)로 쓸 수 있습니다. AM-GM 부등식에 의해, xz + y(x + y + z) ≥ 2√(xz · y(x + y + z)) = 2√(xyz(x + y + z)) = 2입니다. 등호는 xz = y(x + y + z) = 1이고 xyz(x + y + z) = 1일 때 성립합니다. 예를 들어, x = 1, y = √2 - 1, z = 1로 설정할 수 있습니다. 따라서 최소값은 2입니다.

답) 2

334

문제) 다음과 같은 식이 주어졌을 때, ³√2 = a + 1 / (b + 1 / (c + 1 / (d + ⋯)))가 성립합니다. 여기서 a, b, c, d는 양의 정수입니다. b를 구하세요.

풀이) 우리는 다음을 알고 있습니다. ³√2 = a + 1 / (b + 1 / (c + 1 / (d + ⋯))) > a 및 ³√2 = a + 1 / (b + 1 / (c + 1 / (d + ⋯))) < a + 1 이 성립합니다. 따라서 a < ³√2 < a+1이므로 a = 1입니다.

그러면 ³√2 - 1 = 1 / (b + 1 / (c + 1 / (d + ⋯))) 이므로 1 / (³√2 - 1) = b + 1 / (c + 1 / (d + ⋯)) 이 성립합니다. 그러므로 b < 1 / (³√2 - 1) = ³√4 + ³√2 + 1 < b + 1이 성립하고 ³√4 + ³√2 + 1를 잘 계산하면 3과 4 사이의 값임을 알 수 있습니다. 따라서 b = 3입니다.

답) 3

335

문제) 만약 a + b = 8, b + c = -3, a + c = -5라면, 곱 abc의 값은 얼마입니까?

풀이) 첫 번째 주어진 식에 두 번째 식을 더하면, a + 2b + c = 5가 됩니다. 그런 다음, 이 식에서 세 번째 주어진 식을 빼면, 2b = 10이 되어 b = 5가 됩니다. 이 b 값을 첫 번째 주어진 식에 대입하면, a = 3임을 알 수 있습니다. 이 a 값을 세 번째 주어진 식에 대입하면, c = -8임을 알 수 있습니다. 따라서, 곱 abc = 3 · 5 · (-8) = -120입니다.

답) -120

336

문제) 피보나치 수열은 1, 1, 2, 3, 5, ... 와 같이 각 항이 이전 두 항의 합인 수열입니다. 이 수열의 100번째 항을 4로 나눈 나머지는 얼마입니까?

풀이) 수열의 항을 4로 나눈 나머지를 보면, 주기가 6인 패턴을 따릅니다: F₁ ≡ 1 (mod 4), F₂ ≡ 1 (mod 4), F₃ ≡ 2 (mod 4), F₄ ≡ 3 (mod 4), F₅ ≡ 1 (mod 4), F₆ ≡ 0 (mod 4), F₇ ≡ 1 (mod 4), F₈ ≡ 1 (mod 4), ... 따라서, 항들이 반복됩니다. 그러므로 100번째 항은 4번째 항과 같으며, 4로 나누었을 때 나머지는 3입니다.

답) 3

337

문제) 513² - 487²의 값은 무엇인가요?

풀이) 이는 제곱의 차이로, 513² - 487² = (513 + 487)(513 - 487) = 1000 × 26 = 26000입니다.

답) 26000

338

문제) 세 연속된 정수의 곱이 120입니다. 그 곱을 세 정수의 평균으로 나눈 값이 24입니다. 세 연속된 정수 중 가장 큰 수는 무엇입니까?

풀이) 정수를 n-1, n, n+1이라고 합시다. 이들의 평균은 n이고, 이들의 곱은 (n-1)(n)(n+1)=120입니다. 이들의 곱을 평균으로 나눈 값은 (n-1)(n+1)=24입니다. 첫 번째 식을 두 번째 식으로 나누면, n=5가 됩니다. 세 수 중 가장 큰 수는 n+1=6입니다.

답) 6

339

문제) 10진수 999의 6진수 표현은 무엇입니까?

풀이) 6⁴ > 999₁₀ > 6³임을 알고 있습니다. 따라서 10진수 999는 6진수로 네 자리 숫자가 될 것입니다. 6³ = 216이고, 이는 999에 최대 네 번 들어갈 수 있으며, 999 - 4·216 = 135가 남습니다. 6² = 36은 135에 최대 세 번 들어갈 수 있으며, 135 - 3·36 = 27이 남습니다. 그 다음으로, 6¹ = 6은 27에 최대 네 번 들어갈 수 있으며, 27 - 4·6 = 3이 남아 마지막 자릿수가 됩니다. 따라서 10진수 999의 6진수 표현은 4343₆입니다.

답) 4343₆

340

문제) 꼭지점이 (h, k)인 포물선의 방정식이 y = ax² + bx + c일 때, 이 포물선을 y = k에 대해 대칭 이동하면 새로운 포물선의 방정식은 y = dx² + ex + f가 됩니다. a + b + c + d + e + f를 k에 대한 식으로 표현하세요.

풀이) 원래 포물선의 방정식은 다음과 같이 쓸 수 있습니다. y = a(x - h)² + k 대칭 이동된 포물선의 방정식은 다음과 같습니다. y = -a(x - h)² + k 따라서, ax² + bx + c + dx² + ex + f = 2k x = 1일 때, a + b + c + d + e + f = 2k입니다.

답) 2k

341

문제) 벡터 a와 b 사이의 각이 29°이고, 벡터 b와 a - b 사이의 각이 84°일 때, 벡터 a와 a - b 사이의 각을 구하시오.

풀이) 벡터 a, b, a-b는 모두 같은 평면에 놓여 있으므로, 아래의 도형에서 볼 수 있듯이 벡터 a와 a - b 사이의 각은 84° - 29° = 55°입니다. 아래는 도형을 그리는 코드입니다.

unitsize(5 cm);

pair A, B, C, O;

O = (0,0);
A = (1,0);
B = extension(O, O + dir(29), A, A + dir(180 - 55));
C = O + A - B;

draw(O--A,red,Arrow(6));
draw(O--B,green,Arrow(6));
draw(C--A,green,Arrow(6));
draw(O--C,blue,Arrow(6));
draw(B--A,blue,Arrow(6));

label("$\mathbf{a}$", A/2, S);
label("$\mathbf{b}$", B/2, NW);
label("$\mathbf{b}$", (A + C)/2, SE);
label("$\mathbf{a} - \mathbf{b}$", C/2, SW);
label("$\mathbf{a} - \mathbf{b}$", (A + B)/2, NE);
label("$29^\circ$", (0.2,0.05));
label("$55^\circ$", (0.15,-0.05));

답) 55°

342

문제) 자신의 역수의 두 배보다 1 작은 가장 작은 수는 무엇입니까?

풀이) 문제는 x = 2·(1/x) - 1을 만족하는 가장 작은 x 값을 찾으라는 것입니다. 분수를 없애기 위해 x를 곱하고, 항을 정리하면: x² + x - 2 = 0 이 식은 (x + 2)(x - 1) = 0으로 인수분해할 수 있습니다. 또는 이차 방정식 공식을 사용하여 x를 찾을 수도 있습니다: x = (-1 ± √(1² - 4·1·(-2))) / 2 어떤 방법을 사용하든, x = 1 또는 x = -2를 찾을 수 있습니다. 가장 작은 x 값을 원하므로, 답은 -2입니다.

답) -2

343

문제) 어떤 정수 x가 다음 부등식을 만족합니까? 1/4 < x/7 < 1/3

풀이) 부등식의 모든 항에 7을 곱하면, 7/4 < x < 7/3이 됩니다. 7/4는 1과 2 사이에 있고, 7/3은 2와 3 사이에 있으므로, 이 두 분수 사이에 있는 유일한 정수 x는 2입니다.

답) 2

344

문제) 각 자동차 번호판은 2개의 서로 다른 문자(A부터 Z까지)와 2개의 서로 다른 한 자리 숫자(0-9)로 구성될 때, 몇 개의 번호판을 만들 수 있습니까?

풀이) 첫 번째 문자는 알파벳 26자 중 하나를 선택할 수 있고, 두 번째 문자는 남은 25자 중 하나를 선택할 수 있습니다. 첫 번째 숫자는 10개의 숫자 중 하나를 선택할 수 있으며, 두 번째 숫자는 남은 9개 중 하나를 선택할 수 있습니다. 따라서 번호판의 수는 26 × 25 × 10 × 9 = 58,500개입니다.

답) 58,500

345

문제) 함수 f(n) 이 다음과 같이 정의되어 있습니다. f(n) = 4n+3 (if n < a), 7n-12(if n ≥ a). 함수 y = f(n) 의 그래프가 연속이 되도록 하는 a 를 찾으세요.

풀이) 그래프가 연속이 되기 위해서는 함수의 두 부분이 n = a 에서 만나야 합니다. 이를 위해 4a + 3 = 7a - 12 가 성립해야 합니다. a 를 구하면, a = 15 / 3 = 5 입니다.

답) 5

346

문제) 함수 t(x) = 3 - g(x)이고, g(x) = √(x)일 때, t(g(16))은 무엇입니까?

풀이) g(16) = 4이므로, t(g(16)) = t(4) = 3 - g(4) = 3 - √(4) = 3 - 2 = 1입니다.

답) 1

347

문제) 양수인 값의 x를 구하세요. 단, 3제곱근( x² - 4x + 4 ) = 16 입니다.

풀이) 양변을 세제곱하여 x² - 4x + 4 = 16³ 을 얻습니다. x² - 4x + 4 = (x-2)² 임을 주목하세요. 따라서, x-2 = ± 16^3/2 = ± 64 입니다. 따라서, 가능한 x의 값은 -62와 66이며, 유일한 양수 값은 66입니다.

답) 66

348

문제) 다항식 4(3r³+5r-6)-6(2r³-r²+4r)을 간단히 하고, 답을 Ar² + Br + C의 형태로 표현하세요. 여기서 A, B, C는 정수입니다.

풀이) 분배법칙을 사용하고 같은 항끼리 결합하면, 4(3r³+5r-6)-6(2r³-r²+4r) = 12r³+20r-24-12r³+6r²-24r 입니다. 이를 간단히 하면, 6r²-4r-24가 됩니다.

답) 6r²-4r-24

349

문제) 31개 중에서 28개를 선택하는 조합을 계산하세요.

풀이) 아래는 계산 과정입니다. 31개 중에서 28개를 선택하는 조합은 31개 중에서 3개를 선택하는 조합과 같습니다. 31! / (28! × 3!) = (31 × 30 × 29) / (3 × 2 × 1) 31 × (30 / (3 × 2 × 1)) × 29 31 × 5 × 29 결과는 4495입니다.

답) 4495

350

문제) 8명이 각각 한 변에 2명씩 앉을 수 있는 정사각형 테이블에 앉는 방법은 몇 가지입니까? (한 배열이 다른 배열의 회전인 경우 두 배열은 동일한 것으로 간주됩니다.)

풀이) 사람들을 테이블 주위에 배치하는 방법은 8! 가지가 있지만, 이는 각 유효한 배열을 4번씩 계산한 것입니다 (각 사람을 시계 방향으로 2, 4, 또는 6자리 이동하면 동일한 배열이 됩니다). 따라서 답은 8! / 4 = 10080입니다.

답) 10080

351

문제) 18⁶의 일의 자리 숫자를 찾으세요.

풀이) 18⁶의 일의 자리 숫자는 8⁶의 일의 자리 숫자와 같습니다. 8⁶ = 2¹⁸이므로, 2의 거듭제곱의 일의 자리 숫자 패턴을 찾는 것이 쉽습니다. 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32입니다. 이 패턴을 사용하여, 일의 자리 숫자는 4임을 알 수 있습니다.

답) 4

352

문제) 다음을 단순화하세요. cos(2π / 15) cos(4π / 15) cos(8π / 15) cos(16π / 15)

풀이) x = cos(2π / 15) cos(4π / 15) cos(8π / 15) cos(16π / 15)라고 합시다. 그러면 이중각 공식을 반복적으로 적용하여, x sin(2π / 15) = sin(2π / 15) cos(2π / 15) cos(4π / 15) cos(8π / 15) cos(16π / 15) = 1/2 sin(4π / 15) cos(4π / 15) cos(8π / 15) cos(16π / 15) = 1/4 sin(8π / 15) cos(8π / 15) cos(16π / 15) = 1/8 sin(16π / 15) cos(16π / 15) = 1/16 sin(32π / 15) = 1/16 sin(2π / 15), 따라서 x = 1/16입니다.

답) 1/16

353

문제) 삼각형 ABC는 이등변 삼각형이며, AB=AC이고 높이 AM=11입니다. 선분 AM 위에 점 D가 있으며 AD=10이고 ∠BDC = 3∠BAC입니다. 삼각형 ABC의 둘레를 구하세요. 아래는 도형을 그리는 코드입니다.

unitsize(0.4 cm);

pair A, B, C, D, M;

A = (0,11);
D = (0,1);
B = (-11/2,0);
C = (11/2,0);
M = (B + C)/2;

draw(A--B--C--cycle);
draw(A--M);
draw(B--D--C);

label("$A$", A, N);
label("$B$", B, SW);
label("$C$", C, SE);
label("$D$", D, NW);
label("$M$", M, S);

풀이) θ = ∠BAM이라고 하자. 그러면 ∠BDM = 3θ입니다. ∠BDM은 삼각형 ABD의 외각이므로, ∠BDM = ∠BAD + ∠ABD입니다. 따라서, ∠ABD = ∠BDM - ∠BAD = 2θ입니다. 삼각형 ABD에 대해 사인 법칙을 적용하면, BD / sin(θ) = AD / sin(2θ). 따라서 BD / sin(θ) = 10 / (2 sin(θ) cos(θ)) = 5 / (sin(θ) cos(θ)), 따라서 cos(θ) = 5 / BD입니다. 그러면 AB = AM / cos(θ) = 11 / (5 / BD) = (11 / 5) BD입니다. 피타고라스 정리를 직각삼각형 AMB와 DMB에 적용하면, BM² + 11² = AB², BM² + 1² = BD². 이 두 식을 빼면, AB² - BD² = 120. 따라서 (121 / 25) BD² - BD² = 120, 따라서 BD = 5√5 / 2입니다. 그러면 AB = 11√5 / 2이고, BM = 11 / 2입니다. 따라서 삼각형 ABC의 둘레는 AB + AC + BC = (11 / 2)√5 + (11 / 2)√5 + 11 = 11√5 + 11입니다.

답) 11√5 + 11

354

문제) 6권의 서로 다른 책이 있고, 그 중 2권은 수학 책이라고 가정합시다. 수학 책이 서로 붙어 있지 않도록 6권의 책을 선반에 쌓는 방법은 몇 가지입니까?

풀이) 먼저 수학 책이 아닌 책을 배치합니다. 첫 번째 책을 선택하는 데 4가지, 두 번째 책을 선택하는 데 3가지, 세 번째 책을 선택하는 데 2가지, 마지막 책을 선택하는 데 1가지 방법이 있습니다. 그런 다음 네 권의 수학 책이 아닌 책 사이에 두 권의 수학 책을 배치해야 하며, 두 수학 책 사이에는 적어도 한 권의 수학 책이 아닌 책이 있어야 합니다. 네 권의 수학 책이 아닌 책에 의해 총 5개의 빈 공간이 생성됩니다. 따라서 첫 번째 수학 책은 5가지 선택이 가능하고, 두 번째 수학 책은 4가지 선택이 가능합니다. 따라서 책을 배치할 수 있는 총 방법의 수는 4 × 3 × 2 × 1 × 5 × 4 = 480입니다.

답) 480

355

문제) 27개의 연속된 양의 정수의 합이 3⁷입니다. 이들의 중앙값은 무엇입니까?

풀이) 연속된 양의 정수 집합의 중앙값은 그 집합의 평균과 같습니다. 따라서, 중앙값을 구하기 위해 합을 정수의 개수로 나눕니다: 3⁷ / 3³ = 3⁴ = 81.

답) 81

356

문제) 양의 실수인 a, b, c가 주어졌을 때, 다음 식의 최소값을 구하시오. (a + b + c)[(a + b)² + (a + b + 4c)²] / abc

풀이) AM-GM 부등식에 의해, a + b ≥ 2√(ab) 이므로 (a + b)² ≥ 4ab. 또한 AM-GM 부등식에 의해, (a + 2c) + (b + 2c) ≥ 2√((a + 2c)(b + 2c)) 이므로 (a + b + 4c)² ≥ 4(a + 2c)(b + 2c). 따라서, (a + b)² + (a + b + 4c)² ≥ 4ab + 4(a + 2c)(b + 2c) = 8ab + 8ac + 8bc + 16c² = 8(ab + ac + bc + 2c²). AM-GM 부등식에 의해, ab + ac + bc + 2c² = ab/2 + ab/2 + ac + bc + 2c² ≥ 5√(ab/2 · ab/2 · ac · bc · 2c²) = 5√(a³b³c⁴ / 2). 또한 AM-GM 부등식에 의해, a + b + c = a/2 + a/2 + b/2 + b/2 + c ≥ 5√(a/2 · a/2 · b/2 · b/2 · c) = 5√(a²b²c / 16). 따라서, (a + b + c)[(a + b)² + (a + b + 4c)²] / abc ≥ 8 · 5√(a²b²c / 16) · 5√(a³b³c⁴ / 2) / abc = 100. 평등은 a = b = 2, c = 1일 때 성립하므로 최소값은 100이다.

답) 100

357

문제) 어떤 실수 x 값에 대해 -4 < x⁴ + 4x² < 21이 성립하는지 구하세요. 답을 구간 표기법으로 표현하세요.

풀이) 먼저 y = x²로 정의합시다. 이 값을 부등식에 대입하고 -4, x⁴ + 4x², 21에 각각 4를 더하면 다음과 같습니다: 0 < y² + 4y + 4 < 25. y² + 4y + 4를 인수분해하면 0 < (y + 2)² < 25. 양변에 제곱근을 취하면 0 < |y + 2| < 5가 되고, 이는 y의 해를 위한 두 구간을 제공합니다: -2 < y < 3 또는 -7 < y < -2. 그러나 y = x²이므로 y는 음수가 될 수 없습니다. 따라서 0 ≤ y < 3입니다. 이는 -√3 < x < √3을 의미하며, 원래의 부등식을 만족합니다. 구간 표기법으로는 (-√(3), √(3))입니다.

답) (-√(3), √(3))

358

문제) 54장의 카드가 있는 덱이 있습니다. 이 카드를 x명의 플레이어에게 나누어 주는데, 각 플레이어는 y장의 카드를 받습니다. x는 최소 2명이고, y는 최소 5장일 때, 가능한 x의 값은 몇 개입니까?

풀이) 우리는 xy = 54 = 2 · 3³을 만족하는 x가 최소 2이고 y가 최소 5인 경우를 찾고자 합니다. 따라서 가능한 조합 (x, y)은 (2, 27), (3, 18), (6, 9), (9, 6)입니다. 이러한 조합은 총 4개입니다.

답) 4

359

문제) 다음 방정식의 그래프가 포물선, 원, 타원, 쌍곡선, 점, 직선, 두 직선, 또는 비어 있는지 결정하십시오. (x / 2 - 3)² + y² = 10

풀이) 이 방정식은 원의 방정식처럼 보이지만, x를 x / 2로 대체했습니다. 따라서 이 방정식이 타원을 정의한다고 의심됩니다. 이를 확인하기 위해 다음과 같이 씁니다: (x / 2 - 3)² = 1/4 (x - 6)², 그리고 방정식 (x - 6)² / 4 + y² = 10 이 타원의 방정식임을 알 수 있습니다.

답) 타원

360

문제) 다음 조건을 만족하는 x, y, z에 대해 생각해 봅시다. xyz = 4, x³ + y³ + z³ = 4, xy² + x² y + xz² + x² z + yz² + y² z = 12. xy + yz + zx 의 값을 계산하세요.

풀이) 먼저 s₁ = x + y + z 와 s₂ = xy + xz + yz 라고 합시다. 그러면 s₁ s₂ = (x + y + z)(xy + xz + yz) = x² y + xy² + x² z + xz² + y² z + yz² + 3xyz = 12 + 3 · 4 = 24. 또한, s₁³ = (x + y + z)³ = (x³ + y³ + z³) + 3(x² y + xy² + x² z + xz² + y² z + yz²) + 6xyz = 4 + 3 · 12 + 6 · 4 = 64, 따라서 s₁ = 4 . 그러므로 s₂ = 24 / s₁ = 6 입니다.

답) 6

361

문제) 다음 직선은 매개변수화되어 있으며, 그 방향 벡터는 (-7, b)의 형태입니다. b를 구하세요. 아래는 도형을 그리는 코드입니다.

unitsize(0.4 cm);

pair A, B, l, R;
int i, n;

for (i = -8; i <= 8; ++i) {
 draw((i,-8)--(i,8),gray(0.7));
 draw((-8,i)--(8,i),gray(0.7));
}

draw((-8,0)--(8,0),Arrows(6));
draw((0,-8)--(0,8),Arrows(6));

A = (-5,4);
B = (-1,3);
l = extension(A, B, (-8,0), (-8,1));
R = extension(A, B, (8,0), (8,1));

draw(l--R, red);

label("$x$", (8,0), E);
label("$y$", (0,8), N);

풀이) 직선은 (-5, 4)와 (-1, 3)을 지나므로, 그 방향 벡터는 다음과 같이 비례합니다. (-1, 3) - (-5, 4) = (4, -1) x 좌표가 -7이 되도록 이 벡터에 스칼라 -7/4를 곱할 수 있습니다. 그러면 -7/4 · (4, -1) = (-7, 7/4) 따라서, b = 7/4입니다.

답) 7/4

362

문제) 정삼각형이 포물선 x² = 8y에 내접하고, 삼각형의 한 꼭짓점이 포물선의 꼭짓점과 일치합니다. 이 정삼각형의 변의 길이를 구하세요.

풀이) 포물선의 꼭짓점은 원점입니다. 삼각형의 한 꼭짓점을 A = (a, a² / 8)이라고 합시다. 그러면 대칭에 의해 B = (-a, a² / 8)도 삼각형의 또 다른 꼭짓점입니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.2 cm);

real parab (real x) {
 return(x^2/8);
}

pair A, B, O;

A = (8*sqrt(3),24);
B = (-8*sqrt(3),24);
O = (0,0);

draw(O--A--B--cycle);
draw(graph(parab,-15,15));

dot("$A = (a,\frac{a^2}{8})$", A, E);
dot("$B = (-a,\frac{a^2}{8})$", B, W);
dot("$O = (0,0)$", O, S);

그러면 AB² = (a + a)² = 4a²이고, OA² = a² + a⁴ / 64입니다. 따라서, 4a² = a² + a⁴ / 64입니다. 그러면 3a² = a⁴ / 64이므로, a² = 3 × 64이고, 이는 a = 8√3을 의미합니다. 따라서, 삼각형의 변의 길이는 2a = 16√3입니다.

답) 16√3

363

문제) 두 후보, Dan과 Donald가 학급 회장에 출마합니다. 다른 두 후보, Freddie와 Bernie는 부회장에 출마합니다. 각 후보가 당선될 확률은 50%입니다. Dan과 Freddie가 모두 당선될 확률은 얼마입니까? (답을 분수로 표현하세요.)

풀이) Dan이 당선될 확률은 1/2입니다. Freddie가 당선될 확률도 1/2입니다. 따라서, 둘 다 당선될 확률은 1/2 · 1/2 = 1/4입니다.

답) 1/4

364

문제) 어떤 수의 역수에 3을 더한 값이 그 수로 나눈 7과 같습니다. 그 수는 무엇입니까?

풀이) 수를 x라고 합시다. 문제의 문장을 방정식으로 변환하면 3 + 1/x = 7/x가 됩니다. 양변에서 1/x를 빼면 3 = 6/x가 됩니다. 이 방정식의 양변에 x를 곱하면 3x = 6이 되고, 양변을 3으로 나누면 x = 2가 됩니다.

답) 2

365

문제) 원의 각 점 x² + y² = 25가 점 (4,1)에 대해 반사될 때, 이미지 점들의 집합은 다음 방정식을 만족합니다: x² + ay² + bx + cy + d = 0. 실수 숫자들로 이루어진 순서쌍 (a,b,c,d)를 구하세요.

풀이) 원래 원의 중심은 (0,0)입니다. 점 (0,0)을 점 (4,1)에 대해 반사한 점은 (8,2)이므로, 새로운 원의 방정식은 (x - 8)² + (y - 2)² = 25입니다. 이를 전개하면 x² + y² - 16x - 4y + 43 = 0이 됩니다. 따라서, (a,b,c,d) = (1,-16,-4,43)입니다.

답) (1,-16,-4,43)

366

문제) 양의 정수 a와 b가 gcd(a, b)=210, lcm(a, b)=210³, 그리고 a < b를 만족할 때, a의 가능한 값은 몇 개입니까?

풀이) 210의 소인수 분해는 2·3·5·7이므로, 210³의 소인수 분해는 2³·3³·5³·7³입니다. 주어진 조건 gcd(a, b)=210과 lcm(a, b)=210³에 따라, a=2ᵏ·3^ℓ·5ᵐ·7ⁿ그리고 b=2^p·3^q·5^r·7^s로 표현할 수 있으며, 각 쌍 (k,p),(ℓ,q),(m,r),(n,s)는 (1,3) 또는 (3,1)입니다. 따라서 ab를 만족합니다. 따라서 a<b 조건을 적용하면, 16 / 2=8개의 가능한 a의 선택이 있습니다.

답) 8

367

문제) 합 1+3+5+7+9+dots+195+197+199의 7로 나눈 나머지를 구하세요.

풀이) 합을 직접 계산하여 나머지를 구하는 대신, 각 숫자의 나머지를 구하여 계산을 쉽게 할 수 있습니다. 각 7개의 숫자 그룹은 나머지의 합이 1+3+5+0+2+4+6 ≡ 21 ≡ 0 (mod 7)입니다. 합에는 홀수만 포함되므로, 매 7개의 홀수는 14개의 정수입니다. 각 그룹의 나머지가 7이므로, 이를 무시할 수 있습니다. 199를 14로 나눈 몫은 ⌊199 / 14⌋ = 14로, 이는 합에 포함된 7개의 홀수와 같습니다. 따라서 197과 199이 남으며, 이들의 나머지는 1+3 ≡ 4 (mod 7)입니다.

답) 4

368

문제) 함수 f와 f의 역함수 f^-1가 있다고 가정합시다. 만약 f(1)=2, f(2) = 6, f(3)=5라면, f^-1(f^-1(6))의 값은 무엇입니까?

풀이) 먼저 f(2) = 6이므로 f^-1(6)=2입니다. (함수 f가 역함수를 가진다는 가정은 f(x) = 6인 다른 x 값이 없다는 것을 의미합니다.) 마찬가지로, f(1) = 2이므로 f^-1(2)=1입니다. 따라서 f^-1(f^-1(6))=f^-1(2)=1입니다.

답) 1

369

문제) 삼각형의 두 변의 길이가 각각 8 단위입니다. 세 번째 변의 길이가 정수일 때, 삼각형의 가능한 최대 둘레는 몇 단위입니까?

풀이) 삼각형의 불등식에 따르면, 어떤 두 변의 길이의 합은 세 번째 변의 길이보다 커야 합니다. 즉, 8 + 8 = 16은 세 번째 변의 길이보다 커야 합니다. 세 번째 변의 길이가 정수이므로, 가능한 최대 길이는 15 단위입니다. 따라서 둘레는 8 + 8 + 15 = 31 단위입니다.

답) 31

370

문제) 이 사다리꼴의 넓이는 몇 제곱센티미터입니까? 아래는 도형을 그리는 코드입니다.

defaultpen(linewidth(0.7));
draw((0,0)--(27,0)--(15,9)--(0,9)--cycle);
label("5 cm",(21,4.5),NE);
label("5 cm",(7.5,9),N);
label("3 cm",(0,4.5),W);
label("9 cm",(13.5,0),S);
draw(rightanglemark((0,9),(0,0),(27,0),35));
draw(rightanglemark((0,0),(0,9),(15,9),35));

풀이) 아래 그림에서 점선으로 선분을 그려 사다리꼴을 직사각형과 직각삼각형으로 나눕니다. 직사각형의 넓이는 (5 cm)(3 cm) = 15 cm²이고, 삼각형의 넓이는 1/2 × (3 cm) × (9 cm - 5 cm) = 6 cm²입니다. 직사각형의 넓이와 삼각형의 넓이를 더하면 사다리꼴의 넓이는 21 제곱센티미터입니다. 아래는 도형을 그리는 코드입니다.

defaultpen(linewidth(0.7));
draw((0,0)--(27,0)--(15,9)--(0,9)--cycle);
label("5 cm",(21,4.5),NE);
label("5 cm",(7.5,9),N);
label("3 cm",(0,4.5),W);
label("9 cm",(13.5,0),S);
draw(rightanglemark((0,9),(0,0),(27,0),35));
draw(rightanglemark((0,0),(0,9),(15,9),35));
draw(rightanglemark((15,9),(15,0),(27,0),35));
draw((15,0)--(15,9),linetype("2 4"));

답) 21

371

문제) 벡터 (-2, 0, 7) 와 (3, 4, -5)의 내적을 구하세요.

풀이) 벡터 (-2, 0, 7)와 (3, 4, -5)의 내적은 다음과 같습니다. (-2)·3 + 0·4 + 7·(-5) = -41

답) -41

372

문제) 실수 a, b, c에 대해 다음을 만족한다고 하자: |ax² + bx + c| ≤ 1 모든 0 ≤ x ≤ 1에 대해. |a| + |b| + |c|의 가능한 최대 값을 구하시오.

풀이) x = 0을 대입하면 |c| ≤ 1을 얻습니다. x = 1을 대입하면 |a + b + c| ≤ 1. x = 1/2을 대입하면 |a/4 + b/2 + c| ≤ 1. 다음과 같이 두자: p = c, q = a/4 + b/2 + c, r = a + b + c, 따라서 -1 ≤ p, q, r ≤ 1. a, b, c를 구하면 a = 2p - 4q + 2r, b = -3p + 4q - r, c = p. 따라서 삼각 부등식에 의해, |a| = |2p - 4q + 2r| ≤ |2p| + |4q| + |2r| = 8, |b| = |-3p + 4q - r| ≤ |3p| + |4q| + |r| = 8, |c| = |p| ≤ 1. 따라서, |a| + |b| + |c| = 8 + 8 + 1 = 17. 다항식 f(x) = 8x² - 8x + 1을 고려합니다. 이를 다음과 같이 쓸 수 있습니다: f(x) = 8(x - 1/2)² - 1. 0 ≤ x ≤ 1에 대해, 0 ≤ (x - 1/2)² ≤ 1/4이므로, -1 ≤ f(x) ≤ 1. 따라서, |a| + |b| + |c|의 가능한 최대 값은 17입니다.

답) 17

373

문제) 도형에서, AD = BD = CD이고 ∠BCA = 40°입니다. ∠BAC의 크기는 얼마입니까? 아래는 도형을 그리는 코드입니다.

draw((0,0)--(10,0)--(8.2635,9.8481)--cycle,black+linewidth(1));
draw((10,0)--(20,0)--(8.2635,9.8481),black+linewidth(1));
draw((5,-0.5)--(5,0.5),black+linewidth(1));
draw((15,-0.5)--(15,0.5),black+linewidth(1));
draw((8.6318,4.8359)--(9.6317,5.0122),black+linewidth(1));
label("$A$",(8.2635,9.8481),N);
label("$B$",(0,0),SW);
label("$C$",(20,0),SE);
label("$D$",(10,0),S);

풀이) ∠BCA = 40°이고, 삼각형 ADC는 AD = DC인 이등변삼각형이므로 ∠DAC = ∠ACD = 40°입니다. 삼각형의 내각의 합은 180°이므로, ∠ADC = 180° - ∠DAC - ∠ACD = 180° - 40° - 40° = 100°입니다. ∠ADB와 ∠ADC는 보각이므로, ∠ADB = 180° - ∠ADC = 180° - 100° = 80°입니다. 삼각형 ADB는 AD = DB인 이등변삼각형이므로 ∠BAD = ∠ABD입니다. 따라서, ∠BAD = 1/2(180° - ∠ADB) = 1/2(180° - 80°) = 1/2(100°) = 50°입니다. 따라서, ∠BAC = ∠BAD + ∠DAC = 50° + 40° = 90°입니다.

답) 90°

374

문제) William Sydney Porter는 계산 -3 + 4i / (1 + 2i)를 시도했습니다. 그러나 그는 실수로 마이너스 기호를 놓쳐서 3 + 4i / (1 + 2i) = 11/5 - 2/5i를 찾았습니다. 그가 얻었어야 할 답은 무엇입니까?

풀이) 복소수의 나눗셈을 수행하려면 분모의 켤레복소수로 분자와 분모를 모두 곱합니다. 이 경우, 1 + 2i의 켤레복소수는 1 - 2i입니다. 곱셈을 수행하면: (-3 + 4i) / (1 + 2i) = ((-3 + 4i)(1 - 2i)) / ((1 + 2i)(1 - 2i)) = (-3 + 4i + 6i - 8i²) / (1 + 2i - 2i - 4i²) = (5 + 10i) / 5 = 1 + 2i

답) 1 + 2i

375

문제) 64의 양의 제곱근과 64의 세제곱근의 차이는 무엇입니까?

풀이) 64의 양의 제곱근은 √(64) = 8입니다. 64의 세제곱근은 ³√(64) = 4입니다. 차이는 8 - 4 = 4입니다.

답) 4

376

문제) 만약 A가 500의 양의 약수의 합이라면, A의 서로 다른 소인수의 합은 얼마입니까?

풀이) 먼저 A를 구합니다. 500의 소인수 분해는 2² · 5³입니다. 따라서, A = (1 + 2 + 2²)(1 + 5 + 5² + 5³) = 7 · 156입니다. (1 + 2 + 2²)(1 + 5 + 5² + 5³)가 500의 약수의 합과 같은 이유는, 분배법칙을 적용하면 12개의 항이 나오고, 2² · 5³의 각 약수가 정확히 한 번씩 나타나기 때문입니다. 이제 7 · 156 = 7 · 2² · 3 · 13을 소인수 분해합니다. A의 소인수의 합은 2 + 3 + 7 + 13 = 25입니다.

답) 25

377

문제) 점 P가 직선 y = -x + 6 위에 있으며, 점 A(10, -10)과 O(0, 0)에서 등거리인 점 P의 좌표를 구하세요. 답을 순서쌍 (a, b)로 표현하세요.

풀이) 점 P가 A와 O에서 등거리라면, P는 선분 AO의 수직 이등분선 위에 있어야 합니다. A의 좌표는 (10, -10)이고 O의 좌표는 (0, 0)이므로, AO의 기울기는 (-10 - 0) / (10 - 0) = -1입니다. AO의 수직 이등분선의 기울기는 -1의 역수인 1이어야 하며, AO의 중점 (5, -5)을 지나야 합니다. 따라서 수직 이등분선의 방정식은 y - (-5) = x - 5 또는 y = x - 10입니다. P는 직선 y = x - 10과 y = -x + 6의 교점입니다. 이 두 방정식을 같게 놓고 x를 풀면 -x + 6 = x - 10이 되어 x = 8입니다. 따라서 y = -8 + 6 = -2이고, P의 좌표는 (x, y) = (8, -2)입니다.

답) (8, -2)

378

문제) n의 슈퍼팩토리얼은 n!^{n!^{·^{·^·^n!}}} (n!번 반복)으로 정의됩니다. 4의 일의 자리 숫자는 무엇입니까?

풀이) 4! = 4 × 3 × 2 × 1 = 24이므로, 4의 슈퍼팩토리얼 = 24^{{24^{·^{·^·²⁴}}} (24번 반복)의 일의 자리 숫자를 구해야 합니다. 밑 24의 지수는 짝수, 즉 2n이라고 할 수 있습니다. 그러면 4의 슈퍼팩토리얼 = 24²ⁿ = 576ⁿ입니다. 일의 자리가 6인 두 수의 곱의 일의 자리는 6이 됩니다. 따라서 원하는 답은 6입니다.

답) 6

379

문제) 두 자리 소수 중에서 자릿수의 합이 8인 것은 몇 개입니까?

풀이) 먼저, 자릿수의 합이 8인 두 자리 수를 나열합니다: 17, 26, 35, 44, 53, 62, 71, 80 분명히, 26, 44, 62, 80은 소수가 아닙니다. 35도 소수가 아니지만, 17, 53, 71은 소수입니다 (각 숫자를 그 제곱근보다 작은 모든 소수로 나누어 확인할 수 있습니다). 따라서, 답은 3개의 두 자리 소수입니다.

답) 3

380

문제) 아래 표는 Central H.S. 학생들에 대한 설문 조사에서 버스를 타는 학생들의 비율을 보여줍니다. 각 학년에서 300명의 남학생과 300명의 여학생이 조사되었습니다. 남학생 버스 이용자 수가 여학생 버스 이용자 수의 135%에 가장 가까운 학년은 어느 학년입니까?

풀이) 남학생 버스 이용자 수가 여학생 버스 이용자 수의 135%에 가장 가까운 학년은 남학생 버스 이용 비율이 여학생 버스 이용 비율의 135%에 가장 가까운 학년과 같습니다. 여학생 버스 이용 비율의 135%가 되는 비율을 찾기 위해 각 비율에 1.35를 곱합니다. 9학년에서는 비율이 39.4 × 1.35 = 53.19%입니다. 10학년에서는 비율이 33.1 × 1.35 = 44.685%입니다. 11학년에서는 비율이 13.8 × 1.35 = 18.63%입니다. 12학년에서는 비율이 8.6 × 1.35 = 11.61%입니다. 살펴보면, 12학년의 여학생 버스 이용 비율의 135%가 12학년의 남학생 버스 이용 비율에 가장 가깝습니다. 따라서 답은 12입니다.

답) 12

381

문제) 다음을 푸세요 |x² - 81| / (x² - 36x) < 0.

풀이) 모든 x에 대해 |x² - 81| ≥ 0이며, |x² - 81| = 0은 x = ±9일 때만 성립합니다. 분모는 x(x - 36)으로 인수분해됩니다. 이는 0 < x < 36일 때만 음수입니다. 따라서, 해는 x ∈ (0,9) ∪ (9,36)입니다.

답) (0,9) ∪ (9,36)

382

문제) 두 숫자, x와 y가 구간 (0,3)에서 무작위로 선택됩니다. 길이가 1, x, y인 삼각형이 존재할 확률은 얼마입니까?

풀이) 길이가 1, x, y인 삼각형이 존재하려면 삼각형 부등식이 만족되어야 합니다. 이는 x + y > 1, 1 + x > y, 1 + y > x를 의미합니다. x와 y 축이 있는 평면을 그려 이 부등식들이 모두 만족되는 영역을 음영 처리할 수 있습니다. 아래는 도형을 그리는 코드입니다.

draw((0,0)--(3,0)--(3,3)--(0,3));
draw((0,0)--(0,3));
label("$x$",(3,0),S);
label("$y$",(0,3),W);
fill((1,0)--(3,2)--(3,3)--(2,3)--(0,1)--cycle,gray(.7));
draw((1,-.1)--(1,.1));
draw((2,-.1)--(2,.1));
draw((.1,1)--(-.1,1));
draw((.1,2)--(-.1,2));

draw((1,0)--(0,1));
draw((1,0)--(3,2));
draw((0,1)--(2,3));

전체 정사각형의 면적은 3² = 9입니다. 음영 처리되지 않은 영역의 면적은 2² + 1/2 = 9/2입니다. 따라서, 음영 처리된 영역의 면적은 9/2이고, 그러한 삼각형이 존재할 확률은 (9/2) / 9 = 1/2입니다.

답) 1/2

383

문제) 아래는 도형을 그리는 코드입니다.

unitsize(1 cm);

filldraw((0,0)--(3,0)--(3,2)--(0,2)--cycle,lightgreen);
draw((0,0)--(3,0),linewidth(2*bp));
draw((0,2)--(3,2),linewidth(2*bp));
draw(arc((3,1),1,-90,90),linewidth(2*bp));
draw(arc((0,1),1,90,270),linewidth(2*bp));

사각형 필드는 아래와 같이 운동 트랙으로 둘러싸여 있습니다. 트랙은 필드의 두 변과 두 개의 반원으로 구성되어 있습니다. 트랙의 길이는 400미터입니다. 필드의 가능한 최대 면적은 몇 제곱미터입니까?

풀이) 사각형의 너비를 w, 각 반원의 반지름을 r이라고 하겠습니다. 아래는 도형을 그리는 코드입니다.

unitsize(1 cm);

filldraw((0,0)--(3,0)--(3,2)--(0,2)--cycle,lightgreen);
draw((0,0)--(3,0),linewidth(2*bp));
draw((0,2)--(3,2),linewidth(2*bp));
draw(arc((3,1),1,-90,90),linewidth(2*bp));
draw(arc((0,1),1,90,270),linewidth(2*bp));

label("$w$", (1.5,0), S);
label("$r$", (3,1/2), E);
dot((3,1));

그러면 트랙의 길이는 2w + 2πr = 400이므로, w + πr = 200입니다. AM-GM 부등식에 의해, 200 = w + πr ≥ 2√(wπr)이므로, √(wπr) ≤ 100입니다. 따라서 wπr ≤ 10000이므로, wr ≤ 10000 / π입니다. 그러면 필드의 면적인 2wr은 2wr ≤ 20000 / π를 만족해야 합니다. w = 100이고 r = 100 / π일 때 평등이 성립하므로, 가능한 최대 면적은 20000 / π입니다.

답) 20000 / π

384

문제) 어떤 값의 x에 대해, x² - 5x - 4 ≤ 10이 성립합니까? 답을 구간 표기법으로 표현하세요.

풀이) 재배열하면, x² - 5x - 14 ≤ 0입니다. 왼쪽의 이차식은 (x - 7)(x + 2) ≤ 0으로 인수분해됩니다. 따라서, x - 7과 x + 2는 서로 반대 부호를 가집니다. 그러므로 -2 ≤ x ≤ 7이고, x ∈ [-2, 7]입니다.

답) x ∈ [-2, 7]

385

문제) 다음 식을 x에 대해 단순화하세요: 19x + 1 - 4x - 81.

풀이) 재배열하고 그룹화하면, (19x - 4x) + (1 - 81) = 15x - 80을 얻습니다.

답) 15x - 80

386

문제) Kathy는 유럽 여행을 위해 돈이 필요합니다. 그녀는 은행에 300 미국 달러를 가지고 있지만, 그 중 절반을 영국 파운드로, 나머지 절반을 유로로 인출하고 싶습니다. 그녀는 유로를 파운드보다 얼마나 더 많이 가지게 될까요? 1 파운드 = 1.64 USD, 1 유로 = 1.32 USD라고 가정하고, 결과를 가장 가까운 정수로 반올림하세요.

풀이) Kathy가 그녀의 돈 절반 (300 USD ÷ 2 = 150 USD)을 파운드로 환전한 후, 그녀는 150 USD × (1 파운드 / 1.64 USD) ≈ 91.46 파운드를 가지게 됩니다. 나머지 절반을 유로로 환전한 후, 그녀는 150 USD × (1 유로 / 1.32 USD) ≈ 113.64 유로를 가지게 됩니다. 이 두 값을 빼면, 113.64 - 91.46 = 22.18이 됩니다. 문제에서 가장 가까운 정수로 반올림하라고 했으므로, 22.18을 반올림하여 최종 답은 22입니다.

답) 22

387

문제) 다음 부등식의 해집합에 포함된 정수는 몇 개입니까? |x-2| ≤ 5.6

풀이) 절대값을 제거하면, -5.6 ≤ x-2 ≤ 5.6 또는 -3.6 ≤ x ≤ 7.6이 됩니다. 따라서, x는 -3부터 7까지의 정수가 될 수 있습니다. 이 범위에는 7 - (-3) + 1 = 11개의 정수가 있습니다.

답) 11

388

문제) 함수 f(x) = 5x² + 3x + 4일 때, f(-2)의 값은 얼마입니까?

풀이) f(-2)를 계산해 봅시다. f(-2) = 5(-2)² + 3(-2) + 4 = 5(4) - 6 + 4 = 18

답) 18

389

문제) 함수 g(x) = √((x-3)²-(x-8)²)의 정의역에 있는 가장 작은 실수 x는 무엇입니까?

풀이) 실수 x가 g의 정의역에 포함되기 위한 조건은 (x-3)² - (x-8)² ≥ 0입니다. 이를 전개하고 단순화하면 10x - 55 ≥ 0이 됩니다. 가장 작은 해는 x = 55 / 10 = 11 / 2입니다. 또는, (x-3)² - (x-8)² ≥ 0이라는 이차 방정식을 전개하는 대신, (x-3)²는 수직선에서 x가 3과의 거리의 제곱이고, (x-8)²는 x가 8과의 거리의 제곱임을 관찰할 수 있습니다. 따라서 (x-3)²-(x-8)² ≥ 0은 x가 3보다 8에 더 가까울 때 성립하며, 이는 x ≥ (8+3) / 2 = 11 / 2일 때 성립합니다.

답) 11 / 2

390

문제) 삼각형 RST에서, 주어진 것처럼, sin R = 2 / 5입니다. sin T는 얼마입니까? 아래는 도형을 그리는 코드입니다.

pair R,S,T;
T = (0,0);
S = (2,0);
R = (2,sqrt(21));
draw(R--S--T--R);
draw(rightanglemark(R,S,T,10));
label("$T$",T,SW);
label("$S$",S,SE);
label("$R$",R,NE);
label("$5$",(R+T)/2,NW);

풀이) 삼각형 RST는 직각삼각형이므로, sin R = ST / RT입니다. 따라서 sin R = 2 / 5 = ST / 5입니다. 그러므로 ST = 2입니다. 우리는 sin T = RS / RT임을 알고 있습니다. 피타고라스 정리에 의해, RS = √(RT² - ST²) = √(25 - 4) = √21입니다. 따라서 sin T = √21 / 5입니다.

답) √21 / 5

391

문제) 원점과 그래프 y=1 / √(2)(x²-3) 위의 한 점 사이의 가장 짧은 거리는 √(a)/b로 표현될 수 있습니다. 여기서 a와 b는 양의 정수이며, a는 1보다 큰 정수의 제곱으로 나누어지지 않습니다. a+b를 구하세요.

풀이) 거리 공식을 사용하여, 우리는 √(x² + y²)=√(x² + (1/2)(x⁴ - 6x² + 9))를 최소화하려고 합니다. 일반적으로 이러한 최소화 문제는 미적분을 필요로 하지만, 때때로 작동하는 최적화 방법은 완전제곱을 시도하는 것입니다. 루트 아래에서 1/2의 인수를 꺼내면, (1/√(2)) √(2x² + x⁴ - 6x² + 9) = (1/√(2)) √((x⁴ - 4x² + 4) + 5) = (1/√(2)) √((x² - 2)² + 5). 이 마지막 표현은 제곱이 0일 때 최소화됩니다. 즉, x = √(2)일 때입니다. 그러면 거리는 √(5) / √(2) = √(10) / 2입니다. 따라서 원하는 답은 12입니다.

답) 12

392

문제) 함수 f가 다음과 같이 정의되어 있다고 하자. f(x) = { 3-x, x ≤ 3일 때 -x³ + 2x² + 3x, x > 3일 때 } f^-1(0) + f^-1(6)을 계산하시오.

풀이) f^-1(0)은 f(x) = 0이 되는 x의 값입니다. 함수 f는 구간별로 정의되어 있으므로, x ≤ 3과 x > 3의 두 경우를 고려해야 합니다. x ≤ 3이고 f(x) = 0이라면, 3 - x = 0이 되어 x = 3이 됩니다. 이 값은 x ≤ 3의 조건을 만족합니다. x > 3이고 f(x) = 0이라면, -x³ + 2x² + 3x = 0이 됩니다. 이 방정식은 -x(x - 3)(x + 1) = 0으로 인수분해되므로, x = 0, x = 3, x = -1이 됩니다. 그러나 이 값들 중 어느 것도 x > 3의 조건을 만족하지 않으므로, 해는 x = 3이며, 따라서 f^-1(0) = 3입니다. 이제 f^-1(6)을 계산합니다. 이는 f(x) = 6이 되는 x의 값입니다. x ≤ 3이고 f(x) = 6이라면, 3 - x = 6이 되어 x = -3이 됩니다. 이 값은 x ≤ 3의 조건을 만족합니다. x > 3이고 f(x) = 6이라면, -x³ + 2x² + 3x = 6이 되어, x³ - 2x² - 3x + 6 = 0이 됩니다. 이 방정식은 (x - 2)(x² - 3) = 0으로 인수분해되므로, x = 2, x = √3, x = -√3이 됩니다. 그러나 이 값들 중 어느 것도 x > 3의 조건을 만족하지 않으므로, 해는 x = -3이며, 따라서 f^-1(6) = -3입니다. 따라서, f^-1(0) + f^-1(6) = 3 + (-3) = 0입니다. 아래는 도형을 그리는 코드입니다.

unitsize(3mm);
defaultpen(linewidth(.7pt)+fontsize(8pt));
import graph;

draw((-20,0)--(20,0),Arrows(4));
draw((0,-20)--(0,20),Arrows(4));

real f(real x) {return 3-x;}
real g(real x) {return -x^3+2x^2+3x;}

real x;

draw(graph(f,-15,3),BeginArrow(4));
draw(graph(g,3,4),EndArrow(4));

real eps = 0.2;

draw((-eps,3)--(eps,3));
draw((-eps,0)--(eps,0));
draw((-eps,-3)--(eps,-3));

dot("$(-3,6)$",(-3,6),SW);
dot("$(3,0)$",(3,0),NE);

label("$f(x)$",(3,20.5));
label("$x$",(20.5,-1));

답) 0

393

문제) 점 P에서 정사면체의 다섯 개의 꼭짓점까지의 거리가 각각 3, 7, 8, 9, 11입니다. P에서 여섯 번째 꼭짓점까지의 거리를 구하세요. 아래는 도형을 그리는 코드입니다.

import three;

size(125);
currentprojection = perspective(6,3,1);

triple A, B, C, D, E, F, P;

A = (1,0,0);
B = (-1,0,0);
C = (0,1,0);
D = (0,-1,0);
E = (0,0,1);
F = (0,0,-1);
P = (1.2,1.5,1);

draw(A--P,red);
draw(B--P,red);
draw(C--P,red);
draw(D--P,red);
draw(E--P,red);
draw(F--P,red);

draw(A--C);
draw(A--D);
draw(A--E);
draw(A--F);
draw(C--E--D--F--cycle);
draw(D--B--C,dashed);
draw(B--C,dashed);
draw(B--D,dashed);
draw(B--E,dashed);
draw(B--F,dashed);

label("$P$", P, NE);

풀이) 점 P를 (x, y, z)로 두고, 정사면체의 꼭짓점을 A = (a, 0, 0), B = (-a, 0, 0), C = (0, a, 0), D = (0, -a, 0), E = (0, 0, a), F = (0, 0, -a)로 둡니다. 그러면 P에서 꼭짓점까지의 거리의 제곱은 다음과 같습니다: d_A² = (x - a)² + y² + z², d_B² = (x + a)² + y² + z², d_C² = x² + (y - a)² + z², d_D² = x² + (y + a)² + z², d_E² = x² + y² + (z - a)², d_F² = x² + y² + (z + a)². 여기서 d_A² + d_B² = d_C² + d_D² = d_E² + d_F² = 2x² + 2y² + 2z² + 2a²입니다. 거리 3, 7, 8, 9, 11 중에서 제곱의 합을 쌍으로 계산해보면: 3² + 7² = 58, 3² + 8² = 73, 3² + 9² = 90, 3² + 11² = 130, 7² + 8² = 113, 7² + 9² = 130, 7² + 11² = 170, 8² + 9² = 145, 8² + 11² = 185, 9² + 11² = 202. 130이라는 값이 두 번 반복됩니다. 즉, 여섯 번째 거리는 √(130 - 8²) = √66입니다.

답) √66

394

문제) 힘은 질량과 가속도의 곱이라는 잘 알려진 물리 공식이 있습니다. Jen은 Jack이 야구공을 던지는 것과 같은 힘으로 소프트볼을 던지고 싶어합니다. 소프트볼의 질량이 200g이고 야구공의 질량이 150g일 때, Jen의 공의 가속도와 Jack의 공의 가속도의 비율은 얼마입니까? 비율을 기약분수로 답하세요.

풀이) 만약 j₁이 Jen의 공의 가속도이고 j₂가 Jack의 공의 가속도라면, 다음과 같은 식을 세울 수 있습니다. j₁ · 200 = j₂ · 150 따라서 j₁ / j₂ = 3/4.

답) 3/4

395

문제) 함수 z(x, y)는 포물면을 설명합니다. z = (2x - y)² - 2y² - 3y. 아르키메데스와 브라마굽타가 게임을 하고 있습니다. 아르키메데스가 먼저 x를 선택합니다. 그 후, 브라마굽타가 y를 선택합니다. 아르키메데스는 z를 최소화하려 하고, 브라마굽타는 z를 최대화하려 합니다. 브라마굽타가 최적으로 플레이한다고 가정할 때, 아르키메데스는 어떤 값을 선택해야 할까요?

풀이) z를 전개하면 다음과 같습니다. z = 4x² - 4xy + y² - 2y² - 3y = -y² - (4x + 3)y + 4x². 아르키메데스가 x를 선택한 후, 브라마굽타는 z를 최대화하기 위해 y = -(4x + 3) / 2 를 선택할 것입니다. 그러면 z = -(-(4x + 3) / 2)² - (4x + 3)(-(4x + 3) / 2) + 4x² = 8x² + 6x + 9 / 4. 이 표현을 최소화하기 위해 아르키메데스는 x = -6 / 16 = -3 / 8을 선택해야 합니다.

답) -3 / 8

396

문제) 만약 a = 8이라면, (16√[3]{a²})^1/3의 값은 얼마입니까?

풀이) a² = 64이고, 3제곱근(64) = 4입니다. 따라서, (16√[3]{a²})^1/3 = (16 × 4)^1/3 = 64^1/3 = 4입니다.

답) 4

397

문제) 사각형 ABCD는 넓이가 16 평방 인치인 정사각형입니다. 이 도형은 모든 삼각형이 이등변 삼각형이고, 조각 "e"가 정사각형인 중국 탕그램의 조각을 나타냅니다. 회색 조각의 넓이는 몇 평방 인치입니까? 아래는 도형을 그리는 코드입니다.

fill((2,0)--(4,2)--(4,0)--cycle,gray(.7));
draw((0,0)--(0,4)--(4,4)--(4,0)--cycle,linewidth(1));
draw((0,0)--(4,4),linewidth(1));
draw((1,1)--(2,0)--(4,2),linewidth(1));
draw((0,4)--(3,1)--(3,3),linewidth(1));
label("$A$",(0,4),W);
label("$B$",(4,4),E);
label("$C$",(4,0),E);
label("$D$",(0,0),W);
label("e",(2,1));

풀이) 중심점을 H라고 합시다. ADH는 이등변 직각삼각형입니다. ABCD의 넓이가 16이므로, AD의 길이는 4입니다. 따라서 DH의 길이는 4 / √2 = 2√2입니다. DH와 DC의 표시된 점을 각각 F와 G라고 합시다. 각 ADH가 45도이므로, 각 FDG도 45도입니다. 따라서 e가 정사각형이므로 삼각형 DFG는 이등변 직각삼각형입니다. 따라서 HF = DF = FG입니다. DH = 2√2이므로, 이들은 √2와 같습니다. 따라서 DG의 길이는 2이고, CD의 길이가 4이므로 CG의 길이는 2입니다. 각 FGD가 45도이고 e가 정사각형이므로, BC의 표시된 점을 J라고 하면 각 CGJ도 45도입니다. 따라서 삼각형 CGJ, 즉 회색 조각은 이등변 직각삼각형이며, 한 변의 길이가 2이므로 그 넓이는 (2²) / 2 = 2입니다.

답) 2

398

문제) 만약 3x + 2(1 + x) = 17이라면, 6x + 5의 값은 얼마입니까?

풀이) 첫 번째 방정식의 왼쪽을 전개하고 정리하면 5x + 2 = 17이 됩니다. 양변에서 2를 빼면 5x = 15가 되고, 양변을 5로 나누면 x = 3이 됩니다. 이제 x의 값을 알았으므로, 이를 6x + 5에 대입하면 6(3) + 5 = 18 + 5 = 23이 됩니다.

답) 23

399

문제) 모리셔스의 Navin, 크로아티아의 Luka, 보츠와나의 Ian은 유스 호스텔 로비에서 아르바이트에 대해 이야기하고 있습니다. 그들은 Navin이 시간당 160 루피, Luka가 시간당 25 쿠나, Ian이 시간당 34 풀라를 번다는 것을 알게 됩니다. 1 미국 달러가 32.35 모리셔스 루피, 5.18 크로아티아 쿠나, 6.95 보츠와나 풀라와 동등하다면, 8시간 동안 일한 후 누가 가장 많은 돈을 벌까요?

풀이) 이 문제를 해결하는 가장 쉬운 방법은 임금을 미국 달러로 변환하고 8시간 근무를 무시하는 것입니다. 1시간 동안 Navin은 160 루피 × (1 USD / 32.35 루피) ≈ 4.95 USD를 법니다. Luka는 25 쿠나 × (1 USD / 5.18 쿠나) ≈ 4.83 USD를 법니다. Ian은 34 풀라 × (1 USD / 6.95 풀라) ≈ 4.89 USD를 법니다. 이 숫자들을 비교해보면, Navin이 시간당 가장 높은 임금을 받으며, 따라서 8시간 동안 가장 많은 돈을 벌 것입니다.

답) Navin

400

문제) 313.9에 12.6을 더하시오. 결과를 소수로 나타내시오.

풀이) 아래처럼 자릿수를 맞춰 더한다. 313.9 + 12.6 = 326.5. 소수 첫째 자리에서 9 + 6 = 15이므로 5를 쓰고 1을 올림하여, 다음 자리(1의 자리)에 더해 준다. 따라서 답은 326.5이다.

답) 326.5

401

문제) 중심이 Q인 원에서 반지름 AQ와 BQ는 직각을 이룹니다. 두 개의 작은 영역은 접하는 반원입니다. 중심이 Q인 원의 반지름은 14인치입니다. 작은 반원의 반지름은 얼마입니까? 답을 일반 분수로 표현하세요.

풀이) C와 D를 각각 큰 반원과 작은 반원의 중심이라고 하고, r을 작은 반원의 반지름이라고 합시다. 우리는 QD = QB - DB = 14 - r이고 QC = 7이므로, 삼각형 QCD에 피타고라스 정리를 적용할 수 있습니다. (14 - r)² + 7² = (7 + r)². 양쪽의 이항식을 제곱하고 7² + r²를 양쪽에서 빼면 196 - 28r = 14r이 됩니다. 양쪽에 28r을 더하고 42로 나누면 r = 14 / 3 인치가 됩니다.

size(6cm);
defaultpen(linewidth(.7pt)+fontsize(8pt));
dotfactor=4;

draw((1,0)..(0,1)..(-1,0)..(0,-1)..cycle);
draw((-1,0)--(0,0)--(0,-1));
draw((0,0)..(-.5,-.5)..(-1,0));
draw((0,-1)..(-1/3,-2/3)..(0,-1/3));
draw((-1/2,0)--(0,-2/3));
label("$Q$",(0,0),NE);
label("$A$",(-1,0),W);
label("$B$",(0,-1),S);
label("$C$",(-1/2,0),N);
label("$D$",(0,-2/3),E);
dot((-1/2,0));
dot((0,-2/3));
label("$7$",(-7/20,-1/5),E);
label("$r$",(-1/10,-8/15),SW);

답) 14 / 3

402

문제) 복소수 z가 |z| = 1을 만족한다고 하자. 다음 식의 최대값을 구하시오. |1 + z| + |1 - z + z²|

풀이) 복소수 z를 z = x + yi로 두고, x와 y는 실수라고 하자. |z| = 1이므로, x² + y² = 1이다. 그러면 |1 + z| + |1 - z + z²| = |1 + x + yi| + |1 - x - yi + x² + 2xyi - y²| = |(1 + x) + yi| + |(1 - x + x² - 1 + x²) + (-y + 2xy)i| = |(1 + x) + yi| + |(-x + 2x²) + (-y + 2xy)i| = √((1 + x)² + y²) + √((-x + 2x²)² + (-y + 2xy)²) = √((1 + x)² + y²) + √((-x + 2x²)² + y² (1 - 2x)²) = √((1 + x)² + 1 - x²) + √((-x + 2x²)² + (1 - x²) (1 - 2x)²) = √(2 + 2x) + √(1 - 4x + 4x²) = √(2 + 2x) + |1 - 2x|. 이제 u = √(2 + 2x)로 두자. 그러면 u² = 2 + 2x이므로 √(2 + 2x) + |1 - 2x| = u + |3 - u²|. -1 ≤ x ≤ 1이므로, 0 ≤ u ≤ 2이다. 만약 0 ≤ u ≤ √3이라면, u + |3 - u²| = u + 3 - u² = 13/4 - (u - 1/2)² ≤ 13/4. 등호는 u = 1/2일 때, 즉 x = -7/8일 때 성립한다. 만약 √3 ≤ u ≤ 2라면, u + u² - 3 = (u + 1/2)² - 13/4 ≤ (2 + 1/2)² - 13/4 = 3 < 13/4. 따라서 최대값은 13/4이다.

답) 13/4

403

문제) 시계 방향으로 -4 - 5i를 중심으로 90° 회전을 3 (복소수로서)에 적용합니다. 결과 복소수는 무엇입니까?

풀이) 시계 방향으로 90° 회전은 -i로 곱하는 것에 해당합니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.4 cm);

pair O = (-4,-5), A = (3,0), B = rotate(-90,O)*(A);

draw(O--A,dashed);
draw(O--B,dashed);

dot("$3$", A, NE);
dot("$1 - 12i$", B, SE);
dot("$-4 - 5i$", O, W);

복소수 3의 회전 이미지를 z라고 합시다. 회전의 중심이 -4 - 5i이므로, z - (-4 - 5i) = (-i)(3 - (-4 - 5i)). 이를 풀면, z = 1 - 12i를 얻습니다.

답) 1 - 12i

404

문제) 10진수 629의 7진수와 8진수 표현에서 같은 숫자가 몇 개나 있습니까? 예를 들어, 3진수 121과 5진수 413은 공통된 숫자가 하나 있습니다.

풀이) 먼저, 10진수 629를 두 진수로 변환해 봅시다. 7진수로 변환하기 위해, 7⁴ > 629 > 7³임을 알 수 있습니다. 따라서 10진수 629는 7진수로 네 자리 숫자가 됩니다. 7³ = 343은 629에 최대 한 번 들어갈 수 있으며, 629 - 1·343 = 286이 남습니다. 7² = 49는 286에 최대 다섯 번 들어가며, 286 - 5·49 = 41이 남습니다. 그 다음으로, 7¹ = 7은 41에 최대 다섯 번 들어가며, 41 - 5·7 = 6이 남습니다. 따라서 10진수 629의 7진수 표현은 1556₇입니다. 8진수로 변환하기 위해, 8⁴ > 629 > 8³임을 알 수 있습니다. 따라서 10진수 629는 8진수로 네 자리 숫자가 됩니다. 8³ = 512는 629에 최대 한 번 들어갈 수 있으며, 629 - 1·512 = 117이 남습니다. 8² = 64는 117에 최대 한 번 들어가며, 117 - 1·64 = 53이 남습니다. 그 다음으로, 8¹ = 8은 53에 최대 여섯 번 들어가며, 53 - 6·8 = 5가 남습니다. 따라서 10진수 629의 8진수 표현은 1165₈입니다. 마지막으로, 1556₇과 1165₈을 비교하면, 숫자 1, 5, 6이 두 숫자에 모두 존재함을 알 수 있습니다. 따라서 공통된 숫자는 3개입니다.

답) 3

405

문제) Roslyn에게는 10개의 상자가 있습니다. 그 중 5개의 상자에는 연필이 들어 있고, 4개의 상자에는 펜이 들어 있으며, 2개의 상자에는 펜과 연필이 모두 들어 있습니다. 펜과 연필이 모두 들어 있지 않은 상자는 몇 개입니까?

풀이) 연필이 들어 있는 5개의 상자 중 2개는 펜도 들어 있으므로, 연필만 들어 있는 상자는 5 - 2 = 3개입니다. 마찬가지로, 펜이 들어 있는 4개의 상자 중 2개는 연필도 들어 있으므로, 펜만 들어 있는 상자는 4 - 2 = 2개입니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.05cm);
label("Pencils", (2,74));
label("Pens", (80,74));
draw(Circle((30,45), 22));
draw(Circle((58, 45), 22));
label("$2$", (44, 45));
label(scale(0.8)*"$3$",(28,58));
label(scale(0.8)*"$2$",(63,58));

이로써 펜, 연필 또는 둘 다 들어 있는 상자는 3 + 2 + 2 = 7개입니다. 따라서 펜과 연필이 모두 들어 있지 않은 상자는 10 - 7 = 3개입니다.

답) 3

406

문제) 아무도 사무실을 공유하지 않는다면, 3명을 5개의 다른 사무실에 배정하는 방법은 몇 가지입니까? (각 사람은 정확히 하나의 사무실을 받습니다).

풀이) 세 사람을 1, 2, 3으로 번호를 매긴다면, 사람 1은 5개의 사무실 중 하나에 배정될 수 있고, 사람 2는 4개의 사무실 중 하나에 배정될 수 있으며, 사람 3은 3개의 사무실 중 하나에 배정될 수 있습니다. 따라서 5 × 4 × 3 = 60가지 방법으로 세 사람을 사무실에 배정할 수 있습니다.

답) 60

407

문제) 2004를 12로 나눈 나머지는 얼마입니까?

풀이) 정수는 3과 4로 모두 나누어질 때에만 12로 나누어집니다. 2 + 0 + 0 + 4 = 6은 3으로 나누어지므로, 2004는 3으로 나누어집니다. 또한, 2004의 마지막 두 자리는 4의 배수를 형성하므로, 2004는 4로도 나누어집니다. 따라서, 2004는 12로 나누어지며 12로 나눌 때 나머지는 0입니다.

답) 0

408

문제) 함수 f(x) = 2 / (x + 1)일 때, f^-1(1 / 5)의 값을 구하세요.

풀이) f^-1(1 / 5)는 f(x) = 1 / 5가 되는 x 값으로 정의됩니다. 따라서 다음 방정식을 풉니다: 2 / (x + 1) = 1 / 5. 양변에 5(x + 1)을 곱하면, 10 = x + 1. 양변에서 1을 빼면 x = 9가 됩니다.

답) 9

409

문제) 반사 변환이 벡터 (5, 0)을 (4, 3)으로 이동시킵니다. 반사 변환이 벡터 (-2, 3)을 어디로 이동시키는지 구하세요.

풀이) 벡터 (5, 0)과 (4, 3)의 중점은 ( (5 + 4) / 2, (0 + 3) / 2 ) = (9 / 2, 3 / 2) 입니다. 이는 반사되는 벡터가 (9 / 2, 3 / 2)의 스칼라 배수임을 나타냅니다. 따라서 반사되는 벡터는 (3, 1)이라고 가정할 수 있습니다. 아래는 도형을 그리는 코드입니다.

usepackage("amsmath");

unitsize(1 cm);

pair A, B, M, O, R, S;

O = (0,0);
A = (5,0);
R = (4,3);
B = (-2,3);
S = (1/5,-18/5);
M = (A + R)/2;

draw((-3,-1)--(5,5/3),red + dashed);
draw(O--M,red,Arrow(6));
draw((-4,0)--(6,0));
draw((0,-4)--(0,4));
draw(O--A,Arrow(6));
draw(O--R,Arrow(6));
draw(A--R,dashed,Arrow(6));
draw(O--B,Arrow(6));
draw(O--S,Arrow(6));
draw(B--S,dashed,Arrow(6));
label("$$\begin{pmatrix} 5 \\ 0 \end{pmatrix}$", A, S);
label("$$\begin{pmatrix} 4 \\ 3 \end{pmatrix}$", R, NE);
label("$$\begin{pmatrix} -2 \\ 3 \end{pmatrix}$", B, NW);
label("$$\begin{pmatrix} \frac{9}{2} \\ \frac{3}{2} \end{pmatrix}$", M, N);

벡터 (-2, 3)을 (3, 1) 위로 투영한 결과는 proj_(3, 1) (-2, 3) = ((-2, 3) · (3, 1)) / ((3, 1) · (3, 1)) (3, 1) = (-3 / 10) (3, 1) = (-9 / 10, -3 / 10) 입니다. 따라서 벡터 (-2, 3)의 반사 결과는 2(-9 / 10, -3 / 10) - (-2, 3) = (1/5, -18/5) 입니다.

답) (1/5, -18/5)

410

문제) 쌍곡선의 점근선은 y = 2x - 3과 y = 17 - 2x입니다. 또한, 쌍곡선은 점 (4,7)을 지납니다. 쌍곡선의 초점 사이의 거리를 구하세요.

풀이) 점근선의 교점은 (5,7)이므로, 이는 쌍곡선의 중심입니다. 점근선의 기울기가 ±2이므로, 쌍곡선의 방정식은 다음과 같은 형태로 쓸 수 있습니다. (x - 5)² - (y - 7)² / 4 = d 어떤 상수 d에 대해. x = 4, y = 7을 대입하면 d = 1이므로, 방정식은 (x - 5)² / 1 - (y - 7)² / 4 = 1 이 됩니다. 따라서 a² = 1이고 b² = 4이므로 c² = a² + b² = 5이고, 이는 c = √5를 의미합니다. 따라서 초점 사이의 거리는 2c = 2√5입니다.

답) 2√5

411

문제) 숫자 21420N의 일의 자리 숫자를 N이라고 하자. 이 숫자가 6으로 나누어떨어지게 하는 0이 아닌 N의 값은 무엇인가?

풀이) 숫자 21420N이 6으로 나누어떨어지려면 짝수이고, 각 자리 숫자의 합이 3으로 나누어떨어져야 합니다. 따라서 N은 짝수여야 하고, 2 + 1 + 4 + 2 + 0 + N = 9 + N이 3으로 나누어떨어져야 합니다. 9는 이미 3으로 나누어떨어지므로, N도 3으로 나누어떨어져야 합니다. 가능한 숫자는 N = 6입니다.

답) 6

412

문제) 여섯 명의 마녀와 열 명의 마법사가 신비로운 모임에 참석했습니다. 마녀들은 각 마법사와 악수를 하기로 결정했습니다. 마녀들은 이미 서로 친한 친구들이기 때문에 서로 악수하지 않았고, 마법사들은 서로를 싫어해서 다른 마법사들과 악수하지 않았습니다. 모임에서 총 몇 번의 악수가 이루어졌습니까?

풀이) 신비로운 모임에서의 유일한 악수는 6명의 마녀와 10명의 마법사 사이에서 이루어졌습니다. 따라서 모임에서 이루어진 악수는 6 · 10 = 60번입니다.

답) 60

413

문제) 실수 계수를 가진 이차 다항식 P(x)가 모든 실수 x에 대해 다음을 만족한다고 하자: x² - 2x + 2 ≤ P(x) ≤ 2x² - 4x + 3. 또한, P(11) = 181이라고 하자. P(16)을 구하시오.

풀이) 주어진 이차식을 꼭짓점 형태로 다시 쓰면, 다음과 같습니다: 1 + (x-1)² ≤ P(x) ≤ 1 + 2(x-1)². 이 두 이차식은 모두 꼭짓점이 (1, 1)에 있습니다. 이차 함수의 그래프 모양을 고려할 때, P도 꼭짓점이 (1, 1)에 있어야 합니다. 따라서, P(x) = 1 + k(x-1)² 어떤 상수 k에 대해 성립합니다. x = 11일 때, 181 = 1 + 100k이므로, k = 9/5입니다. 그러면, P(16) = 1 + (9/5) · 15² = 406입니다.

답) 406

414

문제) 다음을 간단히 하세요: (10r³)(4r⁶) / 8r⁴.

풀이) 다음을 계산합니다: (10r³)(4r⁶) / 8r⁴ = 40r³⁺⁶ / 8r⁴ = (40 / 8) · r³⁺⁶⁻⁴ = 5r⁵.

답) 5r⁵

415

문제) 다음 방정식을 만족하는 a 값들의 합은 얼마입니까? (3)5² - 4(5-a)² ÷ 3 = 63

풀이) 먼저 분수를 피하기 위해 방정식의 모든 항에 3을 곱한 후 a에 대해 풉니다. 9·5² - 4(5-a)² = 3·63 ⇒ -4(5-a)² = 9·21 - 9·25 ⇒ = 9(-4) ⇒ (5-a)² = 9 따라서, 5-a = 3 또는 5-a = -3 ⇒ 2 = a 또는 8 = a. a 값들의 합은 2 + 8 = 10입니다.

답) 10

416

문제) 129³⁴ + 96³⁸ 을 11로 나눌 때의 나머지는 얼마입니까?

풀이) 우리는 a ≡ b (mod m) 이면 aᶜ ≡ bᶜ (mod m) 이라는 성질을 사용합니다. 129 ≡ -3 (mod 11) 그리고 96 ≡ -3 (mod 11) 이므로, 129³⁴ + 96³⁸ ≡ (-3)³⁴ + (-3)³⁸ ≡ 3³⁴ + 3³⁸ (mod 11) 입니다. 3⁵ ≡ 1 (mod 11) 이므로, 3³⁴ = (3⁵)⁶ · 3⁴ 그리고 3³⁸ = (3⁵)⁷ · 3³ 입니다. 따라서, 129³⁴ + 96³⁸ ≡ (3⁵)⁶ · 3⁴ + (3⁵)⁷ · 3³ ≡ 3⁴ + 3³ ≡ 81 + 27 ≡ 108 ≡ 9 (mod 11) 입니다.

답) 9

417

문제) 다음 값을 계산하세요: sin³ 18° + sin² 18°.

풀이) 우리는 다음과 같이 쓸 수 있습니다. sin³ 18° + sin² 18° = sin² 18° (sin 18° + 1) = sin² 18° (sin 18° + sin 90°). 합을 곱으로 변환하면, sin² 18° (sin 18° + sin 90°) = sin² 18° · 2 sin 54° cos 36° = 2 sin² 18° cos² 36° = (2 sin² 18° cos² 18° cos² 36°) / cos² 18° = (4 sin² 18° cos² 18° cos² 36°) / (2 cos² 18°). 이제 이중각 공식을 사용하면, (4 sin² 18° cos² 18° cos² 36°) / (2 cos² 18°) = (sin² 36° cos² 36°) / (2 cos² 18°) = (4 sin² 36° cos² 36°) / (8 cos² 18°) = sin² 72° / (8 cos² 18°) = 1 / 8. 또한, sin 18° = (√5 - 1) / 4 값을 대입할 수도 있습니다.

답) 1 / 8

418

문제) 다항식 f(x)가 다음과 같다고 하자: f(x) = 3x⁴ + 5x² - 9x - 2. 만약 g(x)가 다항식 f(x-1)과 같다면, g의 계수의 합은 얼마인가?

풀이) g(x)의 계수의 합은 g(1)을 계산하여 찾을 수 있습니다. g(x) = f(x-1)이므로, g(1) = f(1-1) = f(0)입니다. 따라서 계수의 합은 f(0) = -2입니다.

답) -2

419

문제) 점 (6, 0)에서 직선 y = 2x - 2까지의 가장 짧은 거리는 얼마입니까? 답을 가장 간단한 무리수 형태로 표현하세요.

풀이) 점 (6,0)에서 주어진 직선까지의 가장 짧은 선은 직선에 수직일 것입니다. y = 2x - 2에 수직인 직선의 기울기는 -1/2입니다. 이 직선의 방정식은 y = -1/2x + b 형태가 됩니다. 이 직선 위에 점 (6,0)이 있어야 하므로, 다음과 같이 대입합니다: 0 = -1/2 · 6 + b 3 = b 수직선의 방정식은 y = -1/2x + 3입니다. 이제 두 직선이 만나는 점을 구할 수 있습니다: -1/2x + 3 = 2x - 2 5 = 5/2x x = 2 두 직선 중 하나에 대입하면 교점은 (2,2)입니다. 좌표 평면은 다음과 같습니다: 아래는 도형을 그리는 코드입니다.

size(150);
draw((-.5,0)--(7,0));
draw((0,-3)--(0,5));
draw((-.5,-3)--(4,6),linewidth(.7));
draw((6,0)--(0,3),linewidth(.7));
label("$(6,0)$",(6,0),S);
label("$(2,2)$",(2.3,2.1),E);
dot((2,2));
dot((6,0));

점 (6,0)에서 이 점까지의 거리는: √((6-2)² + (0-2)²) = √(16 + 4) = 2√5

답) 2√5

420

문제) 무한히 많은 벡터 v가 존재하여 다음을 만족합니다. (1, 2, -5) × v = (90, 30, 30). 크기가 가장 작은 벡터 v를 찾으세요.

풀이) 벡터 v = (a, b, c)라고 합시다. 그러면 (1, 2, -5) × (a, b, c) = (90, 30, 30)이므로, (5b + 2c, -5a - c, -2a + b) = (90, 30, 30)입니다. 성분을 비교하면 다음과 같습니다. 5b + 2c = 90, -5a - c = 30, -2a + b = 30. 두 번째 방정식에서 c = -5a - 30입니다. 세 번째 방정식에서 b = 2a + 30입니다. 벡터 v의 크기를 최소화하려면 a² + b² + c² = a² + (2a + 30)² + (-5a - 30)² = 30a² + 420a + 1800을 최소화해야 합니다. 제곱을 완성하면 30 (a + 7)² + 330이므로, 크기가 최소화되는 것은 a = -7일 때입니다. 그러면 b = 16이고 c = 5이므로, 우리가 찾는 벡터 v는 (-7, 16, 5)입니다.

답) (-7, 16, 5)

421

문제) 벡터 a 를 b = (2, 6, 3) 에 사영한 결과를 구하세요. 단, a · b = 8 입니다.

풀이) 벡터 a 를 b 에 사영한 결과는 다음과 같습니다. (a · b / b · b) b = (8 / 2² + 6² + 3²) (2, 6, 3) = (16/49, 48/49, 24/49)

답) (16/49, 48/49, 24/49)

422

문제) 만약 arccos x + arccos 2x + arccos 3x = π 라면, x 는 다음과 같은 형태의 3차 다항식을 만족합니다: ax³ + bx² + cx + d = 0 , 여기서 a, b, c, d 는 정수이고, a ≠ 0 입니다. |a| + |b| + |c| + |d|의 가능한 가장 작은 값을 찾으세요.

풀이) arccos x + arccos 2x + arccos 3x = π 에서, arccos x + arccos 2x = π - arccos 3x 이므로 cos (arccos x + arccos 2x) = cos (π - arccos 3x) 입니다. 각도 덧셈 공식을 사용하면, 왼쪽은 다음과 같이 됩니다: cos (arccos x + arccos 2x) = cos (arccos x) cos (arccos 2x) - sin (arccos x) sin (arccos 2x) = (x)(2x) - (√(1 - x²))(√(1 - 4x²)) = 2x² - √((1 - x²)(1 - 4x²)) . 오른쪽은 다음과 같이 됩니다: cos (π - arccos 3x) = -cos (arccos 3x) = -3x , 따라서 2x² - √((1 - x²)(1 - 4x²)) = -3x . 그러면 √((1 - x²)(1 - 4x²)) = 2x² + 3x 입니다. 양변을 제곱하면 (1 - x²)(1 - 4x²) = (2x² + 3x)² 이 됩니다. 이를 정리하면 12x³ + 14x² - 1 = 0 이 됩니다. 따라서 |a| + |b| + |c| + |d|의 가능한 가장 작은 값은 12 + 14 + 0 + 1 = 27 입니다.

답) 27

423

문제) 복소수 α₁, α₂, α₃, α₄는 방정식 x⁴ + 2x³ + 2 = 0의 네 개의 서로 다른 근입니다. 다음의 비정렬 집합을 구하세요. {α₁α₂ + α₃α₄, α₁α₃ + α₂α₄, α₁α₄ + α₂α₃}.

풀이) 기본 대칭 다항식 (s₁ = α₁ + α₂ + α₃ + α₄ = -2, s₂ = α₁α₂ + α₁α₃ + α₁α₄ + α₂α₃ + α₂α₄ + α₃α₄ = 0, s₃ = α₁α₂α₃ + α₂α₃α₄ + α₃α₄α₁ + α₄α₁α₂ = 0, s₄ = α₁α₂α₃α₄ = 2)을 사용하여 다항식 P(x) = (x - (α₁α₂ + α₃α₄))(x - (α₁α₃ + α₂α₄))(x - (α₁α₄ + α₂α₃))을 고려합니다. P는 α₁, α₂, α₃, α₄에 대해 대칭적이므로, 확장된 형태의 계수를 기본 대칭 다항식으로 표현할 수 있습니다. 계산하면 P(x) = x³ - s₂x² + (s₃s₁ - 4s₄)x + (-s₃² - s₄s₁² + s₄s₂) = x³ - 8x - 8 = (x + 2)(x² - 2x - 4) P(x)의 근은 -2와 1 ± √5이므로, 답은 {1 ± √5, -2}입니다.

비고 : x²와 x의 계수는 확장을 통해 쉽게 찾을 수 있으며, 상수항은 (α₁α₂ + α₃α₄)(α₁α₃ + α₂α₄)(α₁α₄ + α₂α₃)의 완전한 확장과 분해 없이도 계산할 수 있습니다. 여기서 구성된 일반 다항식 P는 Galois 이론에서 등장하는 3차 해석식입니다.

답) {1 ± √5, -2}

424

문제) 7로 나누었을 때 나머지가 5이고, 11로 나누었을 때 나머지가 10이며, 13으로 나누었을 때 나머지가 10인 2010보다 작은 가장 큰 정수는 무엇입니까?

풀이) 11과 13으로 나누었을 때 나머지가 10이 되기를 원합니다. 11과 13의 최소공배수는 143입니다. 나머지가 11과 13으로 나누었을 때 10이 되도록 10을 더하여 143 + 10 = 153을 얻습니다. 그러나 이것은 7로 나누었을 때 나머지가 5가 되지 않으므로, 143을 더하여 조건을 만족하는 값을 찾습니다. 153 + 143 + 143 = 439는 7로 나누었을 때 나머지가 5가 됩니다. 2010보다 작은 가장 큰 정수를 원하므로, 7, 11, 13의 최소공배수를 계속 더하여 2010을 넘지 않도록 합니다. 최소공배수는 7 · 11 · 13 = 1001입니다. 439에 1001을 더하여 1440을 얻습니다. 다시 더하면 2010을 초과하므로, 답은 1440입니다.

답) 1440

425

문제) 값 y는 √x에 반비례하며, x=24일 때 y=15입니다. y=3일 때 x는 얼마입니까?

풀이) y와 √x는 반비례 관계이므로, y√x=k라는 상수 k가 존재합니다. 주어진 값을 대입하면, x=24이고 y=15일 때, 15√24=30√6=k입니다. 따라서 y=3일 때, x를 구할 수 있습니다: 3·√x=30√6 ⇒ (√x)² = (10√6)² ⇒ x = 100·6 = 600

답) 600

426

문제) 삼각형 ABC의 무게중심을 G, 수심을 H라고 하자. GH의 중점을 F라고 할 때, AF² + BF² + CF²를 삼각형 ABC의 변의 길이 a, b, c와 외접원의 반지름 R로 표현하시오.

풀이) 삼각형 ABC의 외심 O를 원점으로 하자. 그러면 OG = (OA + OB + OC) / 3 이고 OH = OA + OB + OC 이므로 OF = (2 / 3) (OA + OB + OC) 이다. 그러면

마찬가지로,

따라서, AF² + BF² + CF² = 3R²이다.

답) 3R²

427

문제) 한 정사각형과 한 정삼각형의 둘레가 같습니다. 삼각형의 넓이는 16√3 제곱 센티미터입니다. 정사각형의 대각선의 길이를 센티미터 단위로 구하세요. 답은 가장 간단한 무리수 형태로 표현하세요. 아래는 도형을 그리는 코드입니다.

defaultpen(linewidth(1));
draw((0,0)--(1,0)--(1,1)--(0,1)--cycle);
pair a = (1.25,0)+1.25*dir(60);
pair b = a+1.25*dir(-60);
draw((1.25,0)--a--b--cycle);

풀이) 삼각형의 변의 길이를 x라고 하면, 삼각형의 넓이를 x에 대한 식으로 표현한 후 이를 16√3과 같게 설정하여 x를 구할 수 있습니다. 삼각형의 밑변의 길이는 x입니다. 높이를 구하기 위해, 높이를 그리면 정삼각형이 두 개의 30-60-90 삼각형으로 나뉘며, 가장 긴 변의 길이는 x입니다. 30-60-90 삼각형의 변의 길이 비율은 1:√3:2이므로, 높이는 x√3 / 2의 길이를 가집니다. 따라서 삼각형의 넓이는 1/2 * x * (x√3 / 2) = x²√3 / 4입니다. 이를 16√3과 같게 설정하면, x²√3 / 4 = 16√3이 됩니다. x를 구하면, x = 8입니다. 삼각형의 변의 길이가 8이고 정사각형과 삼각형의 둘레가 같으므로, 정사각형의 변의 길이는 (8 * 3) / 4 = 6입니다. 정사각형의 대각선을 그리면, 이는 두 개의 45-45-90 삼각형으로 나뉘며, 각 변의 길이는 6입니다. 45-45-90 삼각형의 변의 길이 비율은 1:1:√2이므로, 정사각형의 대각선의 길이는 6√2 cm입니다.

답) 6√2

428

문제) 세 자루의 연필과 하나의 점보 지우개가 1.24달러입니다. 다섯 자루의 연필과 하나의 점보 지우개가 1.82달러입니다. 가격에는 세금이 포함되어 있지 않습니다. 연필 한 자루의 가격은 몇 센트입니까?

풀이) 연필의 가격을 p, 점보 지우개의 가격을 e라고 하고, 단위는 센트로 합니다. 주어진 정보를 다음과 같은 연립 방정식으로 나타낼 수 있습니다: 3p + e = 124 5p + e = 182 첫 번째 방정식을 두 번째 방정식에서 빼면 2p = 58이 되고, 따라서 p = 29입니다. 따라서 연필 한 자루의 가격은 29센트입니다.

답) 29

429

문제) 양의 실수인 a, b, c, d가 a + b + c + d = 1을 만족한다고 하자. 다음 식의 최소값을 구하시오. 1/a + 1/b + 4/c + 16/d

풀이) 코시-슈바르츠 부등식에 의해, (a + b + c + d) (1/a + 1/b + 4/c + 16/d) ≥ (1 + 1 + 2 + 4)² = 64 평등은 a = b = c/2 = d/4일 때 발생하며, a + b + c + d = 1을 만족합니다. 이를 풀면 a = 1/8, b = 1/8, c = 1/4, d = 1/2가 되어 최소값은 64입니다.

답) 64

430

문제) 양의 실수 a와 b가 ab² = 5를 만족한다고 하자. a⁴ + b⁸의 최솟값을 구하시오.

풀이) AM-GM 부등식에 의해, a⁴ + b⁸ ≥ 2√(a⁴ b⁸) = 2a² b⁴ = 2(ab²)² = 50. 등호는 a⁴ = b⁸이고 ab² = 5일 때 성립합니다. 이를 풀면 a = √5, b = 5^1/4이므로 최솟값은 50입니다.

답) 50

431

문제) 9 / 2를 소수로 표현하면 무엇입니까?

풀이) 이 문제는 나눗셈으로 해결할 수 있습니다. 또는 분자와 분모에 5를 곱하여 45 / 10을 얻을 수 있습니다. 숫자를 10으로 나누면 소수점이 왼쪽으로 한 자리 이동하므로, 이는 4.5가 됩니다.

답) 4.5

432

문제) 함수 f(x) = (arccos x)² + (arcsin x)² 의 범위를 구하세요. 모든 함수는 라디안 단위입니다.

풀이) 먼저, 모든 x ∈ [-1,1]에 대해 arccos x + arcsin x = π / 2임을 주장합니다. 다음을 주목하세요: cos(π / 2 - arcsin x) = cos(arccos x) = x. 또한, -π / 2 ≤ arcsin x ≤ π / 2이므로, 0 ≤ π / 2 - arcsin x ≤ π입니다. 따라서, π / 2 - arcsin x = arccos x이므로, arccos x + arcsin x = π / 2입니다. α = arccos x, β = arcsin x라고 하면, α + β = π / 2입니다. 그러면 f(x) = (arccos x)² + (arcsin x)² = α² + β² = (π / 2 - β)² + β² = 2β² - πβ + π² / 4 = 2(β - π / 4)² + π² / 8. -π / 2 ≤ β ≤ π / 2이므로, f(x)의 범위는 [π² / 8, 5π² / 4]입니다.

답) [π² / 8, 5π² / 4]

433

문제) 다음 함수가 주어졌을 때, f(n + 1) = (-1)ⁿ⁺¹ n - 2f(n) n ≥ 1이고, f(1) = f(1986)일 때, f(1) + f(2) + f(3) + ... + f(1985)를 계산하세요.

풀이) 다음과 같이 식을 나열할 수 있습니다. f(2) = 1 - 2f(1), f(3) = -2 - 2f(2), f(4) = 3 - 2f(3), f(5) = -4 - 2f(4), ... f(1985) = -1984 - 2f(1984), f(1986) = 1985 - 2f(1985). 이 식들을 모두 더하면, f(2) + f(3) + ... + f(1986) = (1 - 2 + 3 - 4 + ... + 1983 - 1984 + 1985) - 2f(1) - 2f(2) - ... - 2f(1985). 1 - 2 + 3 - 4 + ... + 1983 - 1984 + 1985를 계산하기 위해, 다음과 같이 짝을 지을 수 있습니다. (1 - 2) + (3 - 4) + ... + (1983 - 1984) + 1985 = (-1) + (-1) + ... + (-1) + 1985 = -1984 / 2 + 1985 = 993. 따라서, f(2) + f(3) + ... + f(1986) = 993 - 2f(1) - 2f(2) - ... - 2f(1985). 그러므로, 2f(1) + 3f(2) + 3f(3) + ... + 3f(1985) + f(1986) = 993. f(1986) = f(1)이므로, 3f(1) + 3f(2) + 3f(3) + ... + 3f(1985) = 993. 따라서, f(1) + f(2) + f(3) + ... + f(1985) = 331입니다.

답) 331

434

문제) 57/160을 유한 소수로 변환하세요.

풀이) 유한 소수는 a / 10ᵇ 형태로 쓸 수 있으며, 여기서 a와 b는 정수입니다. 따라서 분모를 10ᵇ 형태로 만들어 봅니다: 57 / 160 = (57 / (2⁵·5)) · ((5⁴) / (5⁴)) = (57·5⁴) / 10⁵ = 35625 / 10⁵ = 0.35625.

답) 0.35625

435

문제) 어떤 이등변 직각삼각형에서 빗변에 대한 높이의 길이가 4√2입니다. 이 삼각형의 넓이는 얼마입니까?

풀이) 이등변 직각삼각형 △ABC에서, 선분 AD는 빗변에 대한 높이입니다. 아래는 도형을 그리는 코드입니다.

import olympiad;
unitsize(0.8inch);
pair A,B,C,D;
A = (0,1);
B= (1,0);
C = -B;
D = (0,0);
draw(A--B--C--A,linewidth(1));
draw(A--D,linewidth(0.8));
draw(rightanglemark(C,A,B,s=5));
draw(rightanglemark(C,D,A,s=5));
label("$A$",A,N);
label("$B$",B,S);
label("$C$",C,S);
label("$D$",D,S);

△ABC는 이등변 직각삼각형이므로, ∠ABC = 45°. ∠ADB = 90°이므로, ∠DAB = 45°입니다. 따라서 △ABD도 45-45-90 삼각형입니다. 마찬가지로, △ACD도 45-45-90 삼각형입니다. 따라서 DB = DC = DA = 4√2이고, BC = BD + DC = 8√2입니다. 따라서 △ABC의 넓이는 (AD)(BC) / 2 = (4√2)(8√2) / 2 = 32입니다.

답) 32

436

문제) 실수 값 함수 f(x) = (2x - 7) / √(x² - 5x + 6)의 정의역은 무엇입니까?

풀이) 함수가 정의되려면 제곱근 안의 값이 양수여야 하므로, x² - 5x + 6 > 0 이어야 합니다. 인수분해하면 (x - 3)(x - 2) > 0이 됩니다. 따라서 왼쪽의 두 인수가 모두 음수이거나 모두 양수여야 합니다. 두 인수가 모두 음수일 때는 x 3입니다. 따라서 f(x)의 정의역은 x 3, 즉 구간 표기법으로 x ∈ (-∞, 2) ∪ (3, ∞)입니다.

답) (-∞, 2) ∪ (3, ∞)

437

문제) n개의 공정한 6면체 주사위를 동시에 굴립니다. 그 중 정확히 두 개의 주사위가 1이 아닌 숫자가 나올 확률이 25 / 216입니다. n을 구하세요.

풀이) n개의 주사위에 대해, 두 개를 선택하는 방법은 ₙC₂ = n(n-1) / 2 가지가 있습니다. 이 방법 각각에 대해, 선택된 두 주사위를 제외한 나머지 주사위가 모두 1이 나올 확률은 (5/6)² (1/6)ⁿ⁻²입니다. 따라서, n에 대해 25n(n-1) / (2 × 6ⁿ) = 25 / 216을 만족하는 값을 찾아야 합니다. 즉, 108n(n-1) = 6ⁿ을 만족하는 n을 찾아야 합니다. n에 값을 대입해보면, n = 4가 작동하며, 4보다 작은 n 값은 작동하지 않습니다. 이제 n이 4보다 큰 값이 작동하지 않음을 증명해야 합니다. n ≥ 5일 때, n < 3ⁿ⁻³이고, n-1 < 2 × 2ⁿ⁻³입니다. 이 부등식을 곱하면, n ≥ 5일 때 n(n-1) < 2 × 6ⁿ⁻³이 되어, 108n(n-1) < 6ⁿ이 됩니다.

답) 4

438

문제) 기호 △, □, ◇, ♣는 1부터 9까지의 네 가지 다른 정수를 나타냅니다. 아래의 방정식을 사용하여 □의 값을 구하세요. △ + □ = ♣ △ + △ = ◇ + ◇ + ◇ + ◇ + ◇ △ + △ = ♣ + ◇

풀이) 간단히 하기 위해, △를 문자 a, □를 문자 b, ◇를 문자 c, ♣를 문자 d로 대체합니다. 주어진 세 방정식은 다음과 같이 됩니다. a + b = d 2a = 5c 2a = c + d 우리는 b의 값을 찾고자 합니다. 두 번째 방정식을 세 번째 방정식에 대입하여 a를 제거하면, 5c = c + d가 되어 4c = d가 됩니다. a, b, c, d는 모두 1부터 9까지의 정수이므로, d는 4 또는 8이어야 하고, c는 각각 1 또는 2가 됩니다. 첫 번째 경우, c = 1이고 d = 4일 때, 세 번째 방정식에 이 값을 대입하면 2a = 5가 되어 a가 정수일 수 없으므로 불가능합니다. 따라서, c = 2이고 d = 8입니다. 이 값을 세 번째 방정식에 대입하여 a를 구하면, 2a = 2 + 8이 되어 a = 5가 됩니다. a = 5와 d = 8을 첫 번째 방정식에 대입하여 b를 구하면, 5 + b = 8이 되어 b = 3이 됩니다. 따라서, □의 값은 3입니다.

답) 3

439

문제) 소수 137 / 500의 소수점 오른쪽에서 마지막으로 0이 아닌 숫자는 무엇입니까?

풀이) 우리는 137 / 500을 274 / 1000의 형태로 다시 쓸 수 있습니다. 따라서 137 / 500 = 274 / 1000 = 0.274이고, 마지막으로 0이 아닌 숫자는 4입니다.

답) 4

440

문제) 다항식 x⁹ + 1을 x - 1로 나눌 때의 몫을 구하세요.

풀이) 우리는 긴 나눗셈을 수행할 수 있습니다. 또한 다음과 같이 쓸 수 있습니다. (x⁹ + 1) / (x - 1) = ((x⁹ - 1) + 2) / (x - 1) = (x⁹ - 1) / (x - 1) + 2 / (x - 1) = x⁸ + x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 + 2 / (x - 1). 따라서, 몫은 x⁸ + x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x + 1입니다.

답) x⁸ + x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + x + 1

441

문제) (u+4)(u-1) - (u-3)(u+6)를 간단히 하세요.

풀이) 첫 번째 곱셈을 전개하면 분배 법칙에 의해 (u+4)(u-1) = u² + 4u - u - 4 = u² + 3u - 4 두 번째 곱셈은 (u-3)(u+6) = u² - 3u + 6u - 18 = u² + 3u - 18 두 식을 빼면, u²와 3u 항이 서로 소거되어 -4 - (-18) = 14가 됩니다.

답) 14

442

문제) Karla는 작년에 차량으로 12,000마일을 운전했습니다. 만약 그녀가 갤런당 평균 48마일을 주행하는 연료 효율이 좋은 하이브리드 자동차를 운전했더라면, 갤런당 평균 15마일을 주행하는 SUV 대신 얼마나 많은 갤런의 휘발유를 절약했을까요?

풀이) Karla는 12,000마일을 운전하기 위해 12,000 / 15 = 800 갤런을 사용했습니다. 만약 그녀가 하이브리드를 운전했다면, 12,000 / 48 = 250 갤런을 사용했을 것입니다. 따라서, 그녀는 800 - 250 = 550 갤런을 절약했을 것입니다.

답) 550

443

문제) 함수 f(x) = 2ˣ가 주어졌습니다. √(f(f(f(f(1)))))의 값을 구하세요.

풀이) 먼저 f(1) = 2¹ = 2입니다. 그 다음, f(f(1)) = f(2) = 2² = 4이고, f(f(f(1))) = f(4) = 2⁴ = 16입니다. 따라서, f(f(f(f(1)))) = f(16) = 2¹⁶이고, √(f(f(f(f(1))))) = √(2¹⁶) = 2⁸ = 256입니다.

답) 256

444

문제) 등차수열 3², x, 3⁴에서 x의 정수 값을 구하세요.

풀이) 항 x는 3² = 9와 3⁴ = 81의 평균입니다. 따라서 (9 + 81) / 2 = 90 / 2 = 45입니다.

답) 45

445

문제) 직사각형 ABCD의 중심을 O라고 하고, AB/AD = k입니다. 직사각형 ABCD의 내부에서 임의의 점을 선택할 때, 그 점이 네 개의 꼭짓점 중 어느 것보다도 O에 더 가까울 확률은 얼마입니까? 아래는 도형을 그리는 코드입니다.

size(200);
draw((-250,100)--(250,100)--(250,-100)--(-250,-100)--cycle);
dot((0,0));
label("$O$",(0,0),N);
label("$A$",(-250,100),NW); label("$B$",(250,100),NE); label("$C$",(250,-100),SE); label("$D$",(-250,-100),SW);

풀이) 원래의 직사각형은 O를 꼭짓점으로 공유하는 네 개의 작은 합동 직사각형으로 나눌 수 있습니다. 이 직사각형들은 모두 유사하므로, 임의의 점 P가 A를 꼭짓점으로 하는 작은 직사각형에 있다고 가정할 수 있습니다. 이 작은 직사각형의 모든 점은 B, C, D보다 A에 더 가깝기 때문에, OP < AP일 확률을 결정해야 합니다.

size(100);
draw((0,0)--(0,100)--(-250,100)--(-250,0)--cycle);
label("$A$",(-250,100),NW); label("$O$",(0,0),SE);
draw((-105,100)--(-145,0));
fill((-105,100)--(-145,0)--(0,0)--(0,100)--cycle, gray(.7));

작은 직사각형의 중심을 기준으로 180도 회전하면 O가 A로 이동하므로, 음영 처리된 영역은 비음영 처리된 영역으로 이동합니다. 따라서 정확히 절반의 면적이 음영 처리되어 있으며, 전체 확률은 k와 무관하게 1/2입니다.

답) 1/2

446

문제) 원의 방정식 x² + y² = 2와 포물선 y² = 8x는 두 개의 공통 접선을 가지며, 이는 네 개의 접점들을 형성합니다. 이 네 개의 접점으로 이루어진 사각형의 넓이를 구하세요. 아래는 도형을 그리는 코드입니다.

unitsize(0.8 cm);

real upperparab (real x) {
 return (sqrt(8*x));
}

real lowerparab (real x) {
 return (-sqrt(8*x));
}

pair A, B, C, D;

A = (-1,1);
B = (2,4);
C = (-1,-1);
D = (2,-4);

draw(graph(upperparab,0,3));
draw(graph(lowerparab,0,3));
draw(Circle((0,0),sqrt(2)));
draw(interp(A,B,-0.2)--interp(A,B,1.2));
draw(interp(C,D,-0.2)--interp(C,D,1.2));
draw(A--C);
draw(B--D);

dot(A);
dot(B);
dot(C);
dot(D);

풀이) 접선의 방정식을 y = mx + b라고 합시다. 이를 x² + y² = 2에 대입하면, (m² + 1) x² + 2bmx + (b² - 2) = 0이 됩니다. 접선이므로 이 이차방정식은 중근을 가지며, 판별식이 0이 됩니다. 따라서 (2bm)² - 4(m² + 1)(b² - 2) = 0이 되고, 이는 b² = 2m² + 2로 단순화됩니다. y = mx + b에서 x를 구하면 x = (y - b) / m이 됩니다. 이를 y² = 8x에 대입하면, y² = (8y - 8b) / m이 되어, my² - 8y + 8b = 0이 됩니다. 이 이차방정식의 판별식도 0이므로, 64 - 4(m)(8b) = 0이 됩니다. 따라서 bm = 2입니다. 그러므로 b = 2 / m입니다. 이를 b² = 2m² + 2에 대입하면, 4 / m² = 2m² + 2가 됩니다. 그러면 4 = 2m⁴ + 2m²가 되어, m⁴ + m² - 2 = 0이 됩니다. 이는 (m² - 1)(m² + 2) = 0으로 인수분해되며, 따라서 m² = 1이므로 m = ±1입니다. m = 1일 때, b = 2입니다. m = -1일 때, b = -2입니다. 따라서 두 접선은 y = x + 2와 y = -x - 2입니다. 아래는 도형을 그리는 코드입니다.

unitsize(0.8 cm);

real upperparab (real x) {
 return (sqrt(8*x));
}

real lowerparab (real x) {
 return (-sqrt(8*x));
}

pair A, B, C, D;

A = (-1,1);
B = (2,4);
C = (-1,-1);
D = (2,-4);

draw(graph(upperparab,0,3));
draw(graph(lowerparab,0,3));
draw(Circle((0,0),sqrt(2)));
draw(interp(A,B,-0.2)--interp(A,B,1.2));
draw(interp(C,D,-0.2)--interp(C,D,1.2));
draw(A--C);
draw(B--D);

label("$y = x + 2$", interp(A,B,1.3), NE);
label("$y = -x - 2$", interp(C,D,1.3), SE);

dot(A);
dot(B);
dot(C);
dot(D);

접선 y = x + 2를 고려합니다. 이를 x² + y² = 2에 대입하면, x² + (x + 2)² = 2가 됩니다. 이는 x² + 2x + 1 = (x + 1)² = 0으로 단순화되며, x = -1이 됩니다. 따라서 원 위의 접점은 (-1,1)입니다. x = y - 2를 대입하면 y² = 8(y - 2)가 됩니다. 이는 (y - 4)² = 0으로 단순화되며, y = 4가 됩니다. 따라서 포물선 위의 접점은 (2,4)입니다. 대칭에 의해 다른 두 접점은 (-1,-1)과 (2,-4)입니다. 문제의 사각형은 밑변이 2와 8이고 높이가 3인 사다리꼴이므로, 그 넓이는 (2 + 8) / 2 × 3 = 15입니다.

답) 15

447

문제) 무한 등비 수열 { 1 / 4, 1 / 8, 1 / 16, dots } 의 처음 n개의 항의 합이 255 / 512 입니다. n을 구하세요.

풀이) 이 수열은 첫 번째 항이 1/4이고 공비가 1/2인 등비 수열입니다. 따라서 처음 n개의 항의 합은 다음과 같습니다: 255 / 512 = (1/4) · ((1 - (1/2)ⁿ) / (1 - 1/2)) = (2ⁿ - 1) / 2ⁿ⁺¹. 255 / 512 = (2⁸ - 1) / 2⁹이므로, n = 8입니다.

답) 8

448

문제) 수학 동아리 모임에 35명의 학생이 참석했습니다. 모임에 참석한 여학생 수는 13의 배수이며, 여학생 수가 남학생 수보다 많습니다. 모임에 참석한 남학생은 몇 명입니까?

풀이) 여학생 수를 0 이상 35 이하의 정수라고 가정합니다. 35보다 작은 13의 배수는 0, 13, 26입니다. 여학생 수가 남학생 수보다 많아야 하므로, 유효한 선택은 여학생이 26명인 경우뿐입니다. 따라서 남학생은 35 - 26 = 9명입니다.

답) 9

449

문제) 다음 식을 계산하세요: 17^-1 (mod 83). 답을 0에서 82 사이의 나머지로 표현하세요. (참고로 17 · 5 = 85임을 고려하면 도움이 될 수 있습니다.)

풀이) 우리는 먼저 17 · 5 = 85 ≡ 2 (mod 83)임을 알 수 있습니다. 그러나 우리는 17 · n ≡ 1 (mod 83)인 n을 찾고자 합니다. 2 · 42 = 84 ≡ 1 (mod 83)임을 주목하세요. 따라서, 17 · 5 · 42 ≡ 2 · 42 ≡ 1 (mod 83), 이것은 17과 5 · 42가 서로의 역수임을 의미합니다. 5 · 42 = 210을 계산할 수 있지만, 이는 0에서 82 사이에 있지 않으므로, 210의 나머지 (mod 83)는 44입니다. 따라서, 17^-1 ≡ 44 (mod 83)입니다. 답을 확인해봅시다: 17 · 44 = 748 = 9 · 83 + 1 ≡ 1 (mod 83), 따라서 우리의 답은 정확합니다.

답) 44

450

문제) 만약 연산 a★b = 9a + 2b - ab + 5 이 정의되어 있을 때, 5★1의 값은 얼마입니까?

풀이) 정의된 함수에 따라, 5★1 = 9(5) + 2(1) - (5)(1) + 5 = 45 + 2 - 5 + 5 = 47 입니다.

답) 47

451

문제) 다음 합동식의 두 개의 가장 작은 양의 정수 해의 평균은 무엇입니까? 14u ≡ 46 (mod 100)

풀이) 14, 46, 100은 모두 공통 인수 2를 가지고 있으므로 이를 나눌 수 있습니다. 따라서 14u ≡ 46 (mod 100)의 해는 7u ≡ 23 (mod 50)의 해와 동일합니다. 왜 그런지 확인해 보세요. 이제 합동식의 양변에 7을 곱하여 49u ≡ 161 (mod 50)를 얻습니다. 이는 이전 합동식과 동일한 해를 가지며, 양변에 7^-1을 곱하여 위의 단계를 역으로 수행할 수 있기 때문입니다. (7과 50은 서로소이므로 7^-1이 mod 50에서 존재합니다.) 49u ≡ 161의 양변을 mod 50에 해당하는 값으로 대체하면, -u ≡ 11 (mod 50)가 되고, 따라서 u ≡ -11 (mod 50)가 됩니다. 이것이 원래 합동식의 해 집합입니다. 두 개의 가장 작은 양의 해는 -11 + 50 = 39와 -11 + 2·50 = 89입니다. 이들의 평균은 64입니다.

답) 64

452

문제) 특정 지도에서 지도상의 3인치는 실제 생활에서 10마일에 해당합니다. 지도에서 두 건물 사이의 실제 거리가 53.25마일일 때, 지도에서 두 건물 사이의 거리는 몇 인치가 될까요? 분수로 표현하세요.

풀이) 지도에서 두 건물 사이의 거리를 d라고 하면, d / 53.25 = 3 / 10 입니다. 교차 곱셈을 통해 d를 구하면, 10d = 159.75가 되어 d = 15.975 인치가 됩니다. 분수로 표현하면, d = 15 + 975 / 1000 = 15 + 39 / 40, 또는 639 / 40 인치입니다.

답) 639 / 40

453

문제) 두 자리 수의 각 자리 숫자의 합이 13입니다. 이 숫자와 그 숫자의 자리 숫자를 뒤집은 숫자와의 차이는 27입니다. 원래 숫자와 자리 숫자를 뒤집은 숫자의 합은 얼마입니까?

풀이) 두 자리 수를 10x + y로 나타낼 수 있습니다. 여기서 x와 y는 숫자이며, x ≠ 0입니다. 각 자리 숫자의 합이 13이므로 x + y = 13입니다. 이 숫자의 자리 숫자를 뒤집으면 10y + x가 됩니다. 차이가 27이라고 주어졌지만, 원래 숫자가 더 큰지 아니면 자리 숫자를 뒤집은 숫자가 더 큰지는 알 수 없습니다. 이를 다음과 같이 나타낼 수 있습니다: |(10x + y) - (10y + x)| = 27. 그러나 두 숫자 중 어느 것이 더 큰지는 중요하지 않으므로, 우리는 그들의 합을 찾고자 합니다. 따라서 일반성을 잃지 않고 첫 번째 숫자가 두 번째 숫자보다 크다고 가정하겠습니다. 이는 x > y를 의미하므로, 절대값을 제거하여 9x - 9y = 27을 얻습니다. 이는 x - y = 3과 같습니다. 이제 두 변수에 대한 두 개의 방정식이 있습니다: x + y = 13과 x - y = 3. 두 방정식을 더하면 2x = 16이므로 x = 8입니다. 빼면 2y = 10이므로 y = 5입니다. 따라서 원래 숫자는 85이고, 답은 85 + 58 = 143입니다. 또는 앞서와 같이 두 자리 수를 10x + y로 표현할 수 있으며, 자리 숫자를 뒤집은 숫자는 10y + x입니다. 이 두 숫자의 합을 구하고자 합니다. (10x + y) + (10y + x) = 11x + 11y = 11(x + y)입니다. 각 자리 숫자의 합이 13이라고 주어졌으므로 x + y = 13입니다. 우리가 원하는 것은 11(x + y)이므로, x + y를 대입하여 11 · 13 = 143이라는 답을 얻을 수 있습니다.

답) 143

454

문제) 7학년과 8학년의 등록 학생 수는 각각 520명과 650명입니다. 두 학년은 학생회에 총 18명의 대표를 가지고 있습니다. 두 학년의 공정한 대표성을 위해 8학년은 몇 명의 대표를 가져야 합니까?

풀이) 8학년은 전체 학생의 650 / (520 + 650) = 650 / 1170 = 65 / 117 만큼을 차지합니다. 이 분수를 더 간단히 하기 위해, 65 = 5 · 13임을 알 수 있습니다. 117은 5로 나누어지지 않으므로, 13으로 나누어지는지 확인해보면 117 = 9 · 13임을 알 수 있습니다. 따라서 공정한 대표성을 가지려면, 8학년은 65 / 117 × 18 = 5 / 9 × 18 = 10명의 대표를 가져야 합니다.

답) 10

455

문제) 행렬 M은 벡터 (2, -1)을 (9, 3)으로, 벡터 (1, -3)을 (7, -1)로 변환합니다. 직선 y = 2x + 1의 M에 의한 상을 구하세요. 답을 "y = mx + b" 형태로 표현하세요.

풀이) 행렬 M이 벡터 (2, -1)을 (9, 3)으로, 벡터 (1, -3)을 (7, -1)로 변환합니다. 따라서 M (6, -3) = (27, 9)입니다. M (6, -3) - M (1, -3) = (27, 9) - (7, -1)입니다. 이는 M (5, 0) = (20, 10)을 의미하므로, M (1, 0) = (4, 2)입니다. 그 다음, M (1, 0) - M (1, -3) = (4, 2) - (7, -1)입니다. 이는 M (0, 3) = (-3, 3)을 의미하므로, M (0, 1) = (-1, 1)입니다. 마지막으로, M (1, 3) = M (1, 0) + 3 M (0, 1) = (4, 2) + 3 (-1, 1) = (1, 5)입니다. 벡터 (0, 1)과 (1, 3)은 직선 y = 2x + 1 위에 있으므로, (−1, 1)과 (1, 5)를 지나는 직선의 방정식을 구해야 합니다. 이 직선의 방정식은 y = 2x + 3입니다.

답) y = 2x + 3

456

문제) 6명의 학생 중에서 5명을 선택하는 방법은 몇 가지입니까?

풀이) 6명의 학생 중에서 5명을 순서에 상관없이 선택하는 방법은 6C5 = 6가지입니다.

답) 6

457

문제) 다항식 x⁴ + 5x³ + 9x² - x - 14 = 0 의 모든 정수 해를 찾으세요. 모든 정수 해를 쉼표로 구분하여 입력하세요.

풀이) 정수 근 정리에 따르면, 가능한 정수 근은 14의 모든 약수(음수 약수 포함)입니다. 즉, -14, -7, -2, -1, 1, 2, 7, 14입니다. 확인해보면, 유일한 정수 해는 -2와 1입니다.

답) -2, 1

458

문제) 54를 6으로 나눈 나머지를 구하세요.

풀이) 54 = 9 · 6 + 0이므로, 54 ≡ 0 (mod 6)입니다.

답) 0

459

문제) 매주 30명에서 50명 사이의 학생들이 Betty와 Wilma가 운영하는 양궁 수업에 참석합니다. 보통 학생들은 표적 연습을 위해 같은 크기의 그룹으로 나뉩니다. 그러나 이번 주에는 Betty가 학생들을 같은 크기의 여러 그룹으로 나눌 수 없다는 것을 알았습니다. Wilma는 그녀와 Betty가 모두 학생들과 함께 연습에 참여하더라도 여전히 궁수들을 같은 크기의 그룹으로 나눌 수 없다는 것을 알았습니다. 이번 주 양궁 수업에 몇 명의 학생이 참석했습니까?

풀이) n을 수업에 참석한 학생 수라고 합시다. Betty는 n이 1과 자기 자신 외에는 약수가 없다는 것을 알았으므로, n은 소수입니다. Wilma는 n + 2도 소수라는 것을 알았습니다. 이는 30과 50 사이에 있는 두 소수 중 2만큼 차이나는 작은 소수를 찾는다는 의미입니다. 그 범위의 소수는 31, 37, 41, 43, 47입니다. 41과 43이 2만큼 차이나므로, n = 41입니다.

답) 41

460

문제) 가짜 금괴는 콘크리트 큐브에 금 페인트를 칠하여 만들어지며, 페인트 비용은 표면적에 비례하고 콘크리트 비용은 부피에 비례합니다. 1인치 큐브를 만드는 데 1.30가 들고 2인치 큐브를 만드는 데 6.80가 든다면, 3인치 큐브를 만드는 데는 얼마가 들까요?

풀이) x를 금 페인트의 제곱인치당 비용, y를 콘크리트의 세제곱인치당 비용이라고 합시다. 1인치 큐브는 표면적이 6인치²이고 부피가 1인치³이므로 총 가격은 6x + y 달러가 됩니다. 마찬가지로, 2인치 큐브는 표면적이 24인치²이고 부피가 8인치³이므로 총 가격은 24x + 8y 달러가 됩니다. 주어진 조건에 따르면, 6x + y = 1.30 24x + 8y = 6.80 첫 번째 방정식에 4를 곱한 것을 두 번째 방정식에서 빼면 4y = 1.60이므로, y = 0.40입니다. 따라서 6x = 0.90이므로, x = 0.15입니다. 3인치 큐브는 표면적이 54인치²이고 부피가 27인치³이므로, 총 가격은 54(0.15) + 27(0.40) = 18.90입니다.

답) 18.90

461

문제) 아래 도형에서, 선분 ST || 선분 QR , ∠P = 40° , ∠Q = 35° 입니다. ∠STR 의 크기를 도 단위로 구하세요. 아래는 도형을 그리는 코드입니다.

pair P,Q,R,SS,T;
Q = (0,0);
R = (1,0);
P = (1.1,0.5);
SS = 0.6*P;
T = R + 0.6*(P-R);
draw(T--SS--P--R--Q--SS);
label("$P$",P,N);
label("$S$",SS,NW);
label("$Q$",Q,S);
label("$R$",R,S);
label("$T$",T,ENE);

풀이) 삼각형 PQR에서, ∠R = 180° - ∠Q - ∠P = 105° 입니다. 선분 ST || 선분 QR이므로, ∠STR = 180° - ∠R = 75° 입니다.

답) 75°

462

문제) 함수 f(n)을 다음과 같이 정의합니다: f(n) = { ⌊n⌋, n ≥ 4일 때 ⌈n⌉, n < 4일 때 } f(π / 3) + f(√(45)) + f(8²/3)를 구하세요.

풀이) 먼저 f(π / 3)을 구해봅시다. π ≈ 3.14이므로, π / 3은 1보다 약간 큽니다. 따라서 f(π / 3) = ⌈π / 3⌉ = 2입니다. 다음으로 f(√(45))를 구해봅시다. √(36) < √(45) < √(49)이므로, 6 < √(45) < 7입니다. 따라서 √(45) ≥ 4이므로, f(√(45)) = ⌊√(45)⌋ = 6입니다. 마지막으로 f(8²/3)를 고려해봅시다. 8²/3 = (∛8)² = 2² = 4이므로, f(8²/3) = ⌊8²/3⌋ = 4입니다. 따라서, f(π / 3) + f(√(45)) + f(8²/3) = 2 + 6 + 4 = 12입니다.

답) 12

463

문제) Linda, Sherry, June, 그리고 Connie는 그들의 동네를 돌아다니며 걸스카우트 쿠키를 팔았습니다. Linda는 27.47를 벌었고, Sherry는 35.23를 벌었으며, June는 37.37를 벌었고, Connie는 26.52를 벌었습니다. 판매 후, 그들은 돈을 모아 은행에 가서 동전을 달러로 바꾸었습니다. 가능한 한 많은 동전을 지폐로 바꾼 후 남은 돈은 몇 센트인가요?

풀이) 큰 숫자를 더하는 대신, 각 사람의 잔액을 찾아 계산을 쉽게 할 수 있습니다. 그들이 번 금액을 센트로 변환하고 각 금액에 대해 100으로 나눈 나머지를 찾습니다. 2747 ≡ 47 (mod 100), 3523 ≡ 23 (mod 100), 3737 ≡ 37 (mod 100), 2652 ≡ 52 (mod 100) 총 센트 수의 100으로 나눈 나머지를 찾고자 합니다. 각 잔액을 더하면 47 + 23 + 37 + 52 ≡ 159 ≡ 59 (mod 100) 따라서 가능한 한 많은 돈을 지폐로 바꾼 후 남은 돈은 59센트입니다.

답) 59

464

문제) 표현식 (x - 5) / (x² - 9)가 정의되지 않는 x의 값은 몇 개입니까?

풀이) 표현식은 분모가 0일 때 정의되지 않습니다. 따라서 x² - 9 = 0이 되는 x의 값을 찾아야 합니다. 이 방정식을 정리하고 양변의 제곱근을 취하면, x² - 9 = 0 → x² = 9 → x = ±3이 됩니다. 따라서 주어진 표현식을 정의되지 않게 만드는 x의 값은 2개입니다.

답) 2

465

문제) 만약 log₆(x-y) + log₆(x+y) = 2이고 log_y 5x = 2라면, x를 구하세요.

풀이) 첫 번째 방정식에서, 차의 제곱 공식에 의해 log₆(x-y) + log₆(x+y) = log₆(x²-y²) = 2가 됩니다. 따라서 x² - y² = 6² = 36입니다. 밑 변환 공식을 사용하여 두 번째 방정식은 log(5x) / log y = 2가 되어 log(5x) = 2log y = log y²가 됩니다. y² = x² - 36을 대입하면 log(x² - 36) = log y² = 2log y = log 5x가 됩니다. 로그 함수는 일대일 함수이므로 x² - 36 = 5x가 되어 x² - 5x - 36 = (x - 9)(x + 4) = 0이 됩니다. 따라서 x = 9, -4이지만, 두 번째 값은 성립하지 않습니다. 따라서 답은 x = 9입니다.

답) 9

466

문제) 양의 약수가 정확히 세 개인 양의 정수를 오름차순으로 나열할 때, 다섯 번째로 나오는 숫자는 무엇입니까?

풀이) 어떤 정수가 두 개 이상의 서로 다른 소인수, 예를 들어, p와 q를 가지면, 그 정수는 적어도 네 개의 양의 약수를 가집니다: 1, p, q, pq. 따라서 약수가 정확히 세 개인 수는 단일 소수의 거듭제곱이어야 합니다. pⁿ의 양의 약수는 1, p, p², p³, ..., pⁿ⁻¹, pⁿ입니다. 따라서 pⁿ은 n+1개의 서로 다른 양의 약수를 가지며, 약수가 정확히 세 개인 양의 정수는 소수의 제곱수입니다. 가장 작은 다섯 개의 그러한 정수는 오름차순으로 2², 3², 5², 7², 11²입니다. 다섯 번째로 나오는 숫자는 11² = 121입니다.

답) 121

467

문제) 만약 rexp(iθ)가 다음 방정식의 해라면, z⁸ - z⁷ + z⁶ - z⁵ + z⁴ - z³ + z² - z + 1 = 0, 여기서 r > 0이고 0 ≤ θ < 2π일 때, 가능한 모든 θ 값의 합을 구하세요.

풀이) 주어진 방정식은 다음과 같이 쓸 수 있습니다. (z⁹ + 1) / (z + 1) = 0. 그러면 z⁹ + 1 = 0, 즉 z⁹ = -1입니다. z = exp(iθ)이므로, exp(9iθ) = -1. 이는 9θ = π + 2πk (k는 정수)라는 의미입니다. 0 ≤ θ < 2π이므로, 가능한 k 값은 0, 1, 2, 3, 5, 6, 7, 8입니다. (k = 4는 제외합니다. 왜냐하면 k = 4일 때 θ = π가 되어 z = -1이 되고, 이는 z + 1 = 0이 되기 때문입니다.) 따라서, 가능한 모든 θ 값의 합은 π / 9 + 3π / 9 + 5π / 9 + 7π / 9 + 11π / 9 + 13π / 9 + 15π / 9 + 17π / 9 = 8π입니다.

답) 8π

468

문제) 도형에서, 음영이 있는 삼각형의 넓이는 얼마입니까? 아래는 도형을 그리는 코드입니다.

fill((0,0)--(2,3)--(10,0)--cycle,gray);
draw((0,0)--(10,0)--(10,3)--(0,3)--cycle,linewidth(1));
draw((0,0)--(2,3)--(10,0),linewidth(1));
label("10 cm",(5,3),N);
label("10 cm",(5,0),S);
label("3 cm",(0,1.5),W);
label("3 cm",(10,1.5),E);
draw((0,2.5)--(.5,2.5)--(.5,3));
draw((10,2.5)--(9.5,2.5)--(9.5,3));

풀이) 음영이 있는 삼각형의 밑변의 길이는 10 cm입니다. 삼각형은 높이가 3 cm인 직사각형 안에 포함되어 있으므로, 삼각형의 높이는 3 cm입니다. (네 변을 가지고 있으며, 두 쌍의 서로 같은 길이의 변과 두 개의 직각을 가진 도형은 직사각형이기 때문입니다.) 따라서 삼각형의 넓이는 1/2 × 3 × 10 = 15 cm²입니다.

답) 15 cm²

469

문제) t의 제곱근이 2보다 크고 3.5보다 작습니다. 이 조건을 만족하는 t의 정수 값은 몇 개입니까?

풀이) 다음과 같은 부등식을 가지고 있습니다: 2 < √(t) < 7 / 2. 이 부등식을 제곱하면 (모든 항이 양수이므로 제곱할 수 있습니다) 4 < t < 49 / 4 = 12.25가 됩니다. 따라서, t는 5에서 12 사이의 정수이며, 이는 t의 가능한 정수 값이 8개임을 의미합니다.

답) 8

470

문제) 다음 식을 평가하세요: ⌈√(20)⌉².

풀이) 16의 제곱근이 √(20)보다 작고, 25의 제곱근이 √(20)보다 크므로, 즉 4 < √(20) < 5입니다. 따라서 √(20)보다 크거나 같은 가장 작은 정수는 5입니다. 그러므로 ⌈√(20)⌉² = 5² = 25입니다.

답) 25

471

문제) 양의 실수인 a, b, c, d가 있고, 이들이 a + b + c + d = 10을 만족한다고 하자. ab²c³d⁴의 최대값을 구하시오.

풀이) AM-GM 부등식에 의해, a + b + c + d = a + b/2 + b/2 + c/3 + c/3 + c/3 + d/4 + d/4 + d/4 + d/4 ≥ 10 ¹⁰√{a(b/2)²(c/3)³(d/4)⁴} = 10 ¹⁰√{ab²c³d⁴ / 27648}. 따라서 a + b + c + d = 10이므로, ab²c³d⁴ ≤ 27648. 평등은 a = 1, b = 2, c = 3, d = 4일 때 성립하므로, 최대값은 27648입니다.

답) 27648

472

문제) 30명의 학생으로 구성된 한 학급이 최근 시험을 보았습니다. 20명의 학생이 80점을, 8명의 학생이 90점을, 2명의 학생이 100점을 받았다면, 이 시험의 학급 평균(산술 평균)은 얼마입니까?

풀이) 주어진 정보에 따르면, 학급이 얻은 총 점수는 다음과 같습니다. 20 × 80 + 8 × 90 + 2 × 100 = 2520 따라서 학급 평균은 2520 / 30 = 84입니다.

답) 84

473

문제) 시속 50마일로, 자동차가 2와 3/4 시간 동안 얼마나 멀리 이동할까요? 답을 대분수로 표현하세요.

풀이) 2시간 동안 시속 50마일로 이동하는 자동차는 50 마일/시간 × 2 시간 = 100 마일을 이동합니다. 이제 자동차가 3/4 시간 동안 얼마나 멀리 이동할 수 있는지 계산해보면, 50 마일/시간 × 3/4 시간 = 150 / 4 = 37과 1/2 마일입니다. 따라서, 자동차는 총 100 + 37과 1/2 = 137과 1/2 마일을 이동합니다.

답) 137과 1/2

474

문제) 아래는 마방진입니다. 각 행, 각 열, 그리고 두 개의 주 대각선의 숫자 합이 모두 같습니다. n의 값은 얼마입니까? 아래는 도형을 그리는 코드입니다.

size(125);
for(int i = 0; i<4; ++i){
 draw((0,i)--(3,i),linewidth(1));
}

for(int j = 0; j<4; ++j){
 draw((j,0)--(j,3),linewidth(1));
}

label("$n-3$",(.5,.5));
label("3",(.5,1.5));
label("$n+1$",(.5,2.5));

label("$n+2$",(1.5,.5));
label("$2n-9$",(1.5,1.5));
label("$1$",(1.5,2.5));

label("$2$",(2.5,.5));
label("$n$",(2.5,1.5));
label("$n-1$",(2.5,2.5));

풀이) 먼저, 첫 번째 행의 합을 계산하면 (n+1) + 1 + (n-1) = 2n + 1이 됩니다. 두 번째 행의 합을 계산하면 3 + (2n-9) + n = 3n - 6이 됩니다. 마방진이므로, 이 두 합은 같아야 합니다. 따라서 2n + 1 = 3n - 6이 됩니다. n을 구하면, n = 7입니다. 정사각형은 다음과 같이 보일 것입니다: 아래는 도형을 그리는 코드입니다.

size(2cm);
draw((0,0)--(3,0)--(3,3)--(0,3)--cycle,linewidth(1));
draw((1,0)--(1,3),linewidth(1));
draw((2,0)--(2,3),linewidth(1));
draw((0,1)--(3,1),linewidth(1));
draw((0,2)--(3,2),linewidth(1));
label("8",(.5,2.5));
label("1",(1.5,2.5));
label("6",(2.5,2.5));
label("3",(.5,1.5));
label("5",(1.5,1.5));
label("7",(2.5,1.5));
label("4",(.5,.5));
label("9",(1.5,.5));
label("2",(2.5,.5));

답) 7

475

문제) 다음 식의 값을 구하세요: log₂3 · log₃4 · log₄5 · log₅6 · log₆7 · log₇8.

풀이) 밑 변환 공식 logₐb = log b / log a 를 사용하여 다음과 같이 계산합니다. log₂3 · log₃4 · log₄5 · log₅6 · log₆7 · log₇8 = (log 3 / log 2) · (log 4 / log 3) · (log 5 / log 4) · (log 6 / log 5) · (log 7 / log 6) · (log 8 / log 7). 이를 간단히 하면 log 8 / log 2 = log₂8 = 3이 됩니다.

답) 3

476

문제) 어떤 불공정한 6면체 주사위를 굴릴 때, 면 F가 나올 확률은 1/6보다 크고, 면 F의 반대편 면이 나올 확률은 1/6보다 작으며, 나머지 면이 나올 확률은 각각 1/6입니다. 각 반대편 면 쌍의 숫자의 합은 7입니다. 두 개의 이러한 주사위를 굴릴 때, 합이 7이 될 확률은 47/288입니다. 면 F가 나올 확률이 m/n이고, 여기서 m과 n은 서로소인 양의 정수일 때, m+n을 구하세요.

풀이) p(a,b)를 첫 번째 주사위에서 a가 나오고 두 번째 주사위에서 b가 나오는 확률이라고 하겠습니다. 그러면 합이 7이 되는 확률은 다음과 같습니다: p(1,6) + p(2,5) + p(3,4) + p(4,3) + p(5,2) + p(6,1). 면 F가 나올 확률을 (1/6) + x라고 하겠습니다. 그러면 면 F의 반대편 면이 나올 확률은 (1/6) - x입니다. 따라서 47/288 = 4(1/6)² + 2((1/6) + x)((1/6) - x) = 4/36 + 2(1/36 - x²) = 1/6 - 2x². 여기서 2x² = 1/288이므로, x = 1/24입니다. 따라서 면 F가 나올 확률은 (1/6) + (1/24) = 5/24이고, m+n = 29입니다.

답) 29

477

문제) 짐과 마사는 직사각형 필드의 모퉁이에 함께 서 있습니다. 짐은 필드를 대각선으로 가로질러 걷습니다. 마사는 필드의 길이와 너비를 따라 같은 위치에 도착합니다. 필드는 너비가 300피트이고 길이가 400피트입니다. 짐이 마사보다 몇 피트 덜 걷습니까?

풀이) 필드의 대각선은 √(300² + 400²) = 500 피트이므로 짐은 500피트를 걷습니다. 필드의 두 인접한 변의 길이는 300 + 400 = 700 피트이므로 마사는 700피트를 걷습니다. 따라서 짐은 마사보다 700 - 500 = 200 피트 덜 걷습니다.

답) 200

478

문제) 두 자리 숫자 "B6"에서 B는 십의 자리 숫자이며, 이 숫자는 양의 정수의 제곱입니다. B의 가능한 서로 다른 값은 몇 개입니까?

풀이) 두 자리 수의 완전 제곱수 중에서, 4² = 16과 6² = 36만이 끝자리가 6입니다. 따라서, B의 가능한 서로 다른 값은 2개입니다.

답) 2

479

문제) 다음 방정식의 모든 복소수 해의 합을 구하세요. 1 / (x² - 1) + 2 / (x² - 2) + 3 / (x² - 3) + 4 / (x² - 4) = 2010x - 4.

풀이) 양변에 4를 더하면 다음과 같습니다. 1 / (x² - 1) + 1 + 2 / (x² - 2) + 1 + 3 / (x² - 3) + 1 + 4 / (x² - 4) + 1 = 2010x. 이는 다음과 같이 단순화됩니다. x² / (x² - 1) + x² / (x² - 2) + x² / (x² - 3) + x² / (x² - 4) = 2010x. x = 0은 해가 되며, 이는 합에 영향을 주지 않습니다. 그렇지 않으면 양변을 x로 나눌 수 있습니다. x / (x² - 1) + x / (x² - 2) + x / (x² - 3) + x / (x² - 4) = 2010. 분모를 제거하면 다음과 같습니다. x(x² - 2)(x² - 3)(x² - 4) + x(x² - 1)(x² - 3)(x² - 4) + x(x² - 1)(x² - 2)(x² - 4) + x(x² - 1)(x² - 2)(x² - 3) = 2010(x² - 1)(x² - 2)(x² - 3)(x² - 4). 이는 다음과 같이 확장됩니다. 4x⁷ + ... = 2010x⁸ + ..., 여기서 차수가 7 이상인 항만 표시됩니다. 따라서 2010x⁸ - 4x⁷ + ... = 0, 비에타의 정리에 의해, 근의 합은 4 / 2010 = 2 / 1005입니다.

답) 2 / 1005

480

문제) 소수 p에 대해 합동식 8x ≡ 1 (mod p)가 해를 가지지 않는 경우가 유한하게 많습니다. 그러한 모든 p의 합을 구하세요.

풀이) 해가 존재하려면 8이 모듈로 p에 대해 가역적이어야 합니다. 즉, gcd(8, p) = 1이어야 합니다. 8 = 2³은 2의 거듭제곱이므로, 8이 모듈로 q에 대해 가역적이려면 q가 홀수여야 합니다. 모든 소수 중 2를 제외한 소수는 홀수이므로, 우리가 찾는 수는 2입니다.

답) 2

481

문제) 복소수 ω 가 ω³ = 1 을 만족한다고 하자. 다음 식의 가능한 모든 값을 구하시오. 1 / 1 + ω + 1 / 1 + ω² 모든 가능한 값을 쉼표로 구분하여 입력하시오.

풀이) 다음과 같이 쓸 수 있습니다. 1 / 1 + ω + 1 / 1 + ω² = 1 + ω² + 1 + ω / (1 + ω)(1 + ω²) = 2 + ω + ω² / 1 + ω + ω² + ω³ = 2 + ω + ω² / 2 + ω + ω² = 1.

답) 1

482

문제) 양의 정수 n이 주어졌을 때, 다음 식을 간단히 하세요. [(2⁴ + 1 / 4)(4⁴ + 1 / 4) ⋯ ((2n)⁴ + 1 / 4)] / [(1⁴ + 1 / 4)(3⁴ + 1 / 4) ⋯ ((2n - 1)⁴ + 1 / 4)].

풀이) 함수 f(m)을 다음과 같이 정의합니다. f(m) = m⁴ + 1/4 = (4m⁴ + 1) / 4 이 식을 약간의 조작을 통해 인수분해할 수 있습니다. f(m) = (4m⁴ + 1) / 4 = (4m⁴ + 4m² + 1 - 4m²) / 4 = ((2m² + 1)² - (2m)²) / 4 = ((2m² + 2m + 1)(2m² - 2m + 1)) / 4. 이제 g(m) = 2m² + 2m + 1로 정의합니다. 그러면 g(m - 1) = 2(m - 1)² + 2(m - 1) + 1 = 2m² - 2m + 1 따라서, f(m) = (g(m) g(m - 1)) / 4 그러므로, [(2⁴ + 1 / 4)(4⁴ + 1 / 4) ⋯ ((2n)⁴ + 1 / 4)] / [(1⁴ + 1 / 4)(3⁴ + 1 / 4) ⋯ ((2n - 1)⁴ + 1 / 4)] = [f(2) f(4) ⋯ f(2n)] / [f(1) f(3) ⋯ f(2n - 1)] = [(g(2) g(1) / 4) · (g(4) g(3) / 4) ⋯ (g(2n) g(2n - 1) / 4)] / [(g(1) g(0) / 4) · (g(3) g(2) / 4) ⋯ (g(2n - 1) g(2n - 2) / 4)] = g(2n) / g(0) = 2(2n)² + 2(2n) + 1 = 8n² + 4n + 1

답) 8n² + 4n + 1

483

문제) 2010보다 작은 양의 홀수를 무작위로 선택했을 때, 그 역수가 유한 소수로 나타날 확률이 a / b 라고 하자. 여기서 a 와 b 는 서로소인 양의 정수이다. 그렇다면 a+b 는 얼마인가?

풀이) 2010보다 작은 양의 정수는 총 2009개이며, 그 중 1005개는 홀수입니다. 1 / n 이 유한 소수라면, n 은 2와 5로만 나누어져야 합니다. 그러나 n 이 홀수여야 한다는 추가 조건이 있으므로, n 은 5의 거듭제곱이어야 합니다. 2010보다 작은 5의 거듭제곱은 다음과 같습니다. 5⁰ = 1, 5¹ = 5, 5² = 25, 5³ = 125, 5⁴ = 625, 5⁵ = 3125 (이 값은 2010보다 큽니다). 따라서 조건을 만족하는 홀수는 5개이며, 원하는 확률은 5 / 1005 = 1 / 201입니다. 이는 기약 분수이므로, 답은 1 + 201 = 202입니다.

답) 202

484

문제) 삼각형 ABC의 넓이는 a² - (b - c)²와 같으며, 여기서 a, b, c는 삼각형 ABC의 변입니다. tan A를 구하세요.

풀이) 삼각형 ABC의 넓이는 다음과 같습니다. 1/2 · b · c · sin A 따라서, 1/2 · b · c · sin A = a² - (b - c)² = a² - b² + 2bc - c²입니다. 코사인 법칙에 따르면, b² + c² - 2bc · cos A = a²이므로 1/2 · b · c · sin A = 2bc - 2bc · cos A입니다. 이를 정리하면 sin A = 4 - 4 · cos A가 됩니다. 양변을 제곱하면, sin² A = 16 - 32 · cos A + 16 · cos² A가 됩니다. 따라서 1 - cos² A = 16 - 32 · cos A + 16 · cos² A입니다. 이를 정리하면 17 · cos² A - 32 · cos A + 15 = 0이 됩니다. 이는 (cos A - 1)(17 · cos A - 15) = 0으로 인수분해됩니다. cos A는 1이 될 수 없으므로, cos A = 15/17입니다. 그러면 sin A = 4 - 4 · cos A = 8/17이므로 tan A = sin A / cos A = 8/15입니다.

답) 8/15

485

문제) 다음을 풀어라 √(x + √(3x + 6)) + √(x - √(3x + 6)) = 6.

풀이) 양변을 제곱하면, x + √(3x + 6) + 2 √(x + √(3x + 6)) √(x - √(3x + 6)) + x - √(3x + 6) = 36. 그러므로 2x + 2 √(x² - 3x - 6) = 36, 따라서 √(x² - 3x - 6) = 18 - x. 양변을 제곱하면, x² - 3x - 6 = 324 - 36x + x². 따라서, x = 10임을 확인할 수 있다.

답) 10

486

문제) 어떤 점 A, B, C, 또는 D에서 시작하여 나머지 세 점을 한 번씩 방문할 때 이동할 수 있는 가장 짧은 거리는 얼마입니까? 아래는 도형을 그리는 코드입니다.

pair A,B,C, D;
A = (-3,3); B = (3,0); C = (0, -4); D = (0,0);
draw(D--B--C--cycle); draw(D--A--B--cycle);draw(D--A--C--cycle);
label("$A$", A, NW);label("$B$", B, E); label("$C$", C, S);label("$D$", D, NE);
label("3", D--B, S); label("6", A--B, NE); label("6", A--C, SW); label("4", D--C, NW+N);
label("5", A--D, SE+NE); label("5", C--B, E);

풀이) 네 개의 점을 모두 방문하기 위해서는 적어도 세 개의 다른 선분을 따라 이동해야 합니다. 가장 짧은 세 선분의 합은 3 + 4 + 5 = 12입니다. 하지만 길이가 12인 경로로는 한 점에서 시작하여 다른 세 점을 방문할 수 없다는 것을 알 수 있습니다. (DB, BC, CD는 점 A를 방문할 수 없으며, AD, CD, BD를 연속적인 경로로 이동하는 것도 불가능합니다.) 이제 길이가 13인 경로를 찾아보면, 점 A에서 D로, D에서 B로, B에서 C로 이동하는 경로가 가능합니다. 또는 B에서 D로, D에서 C로, C에서 A로 이동하는 경로도 가능합니다. 두 경로 모두 길이는 13입니다.

답) 13

487

문제) 반지름이 3인치인 강철 구는 가능한 가장 짧은 변 길이를 가진 정육면체의 모서리에서 금속을 제거하여 만들어집니다. 정육면체의 부피는 몇 입방 인치입니까?

풀이) 반지름이 3인치인 구는 지름이 6인치이며, 최소한 변의 길이가 6인 정육면체에 내접할 수 있습니다. 따라서 가능한 가장 작은 정육면체는 변의 길이가 6이고, 부피는 6³ = 216 입방 인치입니다. 아래는 도형을 그리는 코드입니다.

size(60);
draw(Circle((6,6),4.5));
draw((10.5,6)..(6,6.9)..(1.5,6),linetype("2 4"));
draw((10.5,6)..(6,5.1)..(1.5,6));
draw((0,0)--(9,0)--(9,9)--(0,9)--cycle);
draw((0,9)--(3,12)--(12,12)--(9,9));
draw((12,12)--(12,3)--(9,0));
draw((0,0)--(3,3)--(12,3),dashed); draw((3,3)--(3,12),dashed);

답) 216

488

문제) 다음 합의 4로 나눈 나머지를 구하세요: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12.

풀이) 나머지를 그룹화하면 일부 수열 계산이 더 쉬워집니다: 1 + 2 + 3 + 0 + 1 + 2 + 3 + 0 + 1 + 2 + 3 + 0 ≡ 3(1 + 2 + 3 + 0) ≡ 18 ≡ 2 (mod 4).

답) 2

489

문제) 한 셔츠의 세일 가격이 14.40로 표시되어 있으며, 이는 원래 가격에서 60% 할인된 가격입니다. 셔츠의 원래 가격은 몇 달러였습니까?

풀이) 셔츠가 60% 할인되었다면, 현재 가격은 원래 가격의 0.4배입니다. 따라서 원래 가격은 14.40 / 0.4 = 36달러입니다.

답) 36달러

490

문제) 함수 f(x) = |x - p| + |x - 15| + |x - p - 15|가 주어졌을 때, 0 < p < 15입니다. x가 p ≤ x ≤ 15인 구간에서 f(x)의 최소값을 구하세요.

풀이) 0 < p ≤ x ≤ 15이므로, 절대값을 다음과 같이 단순화할 수 있습니다. f(x) = (x - p) - (x - 15) - (x - p - 15) = -x + 30 이 표현식의 값은 x = 15일 때 최소화되며, 이때 -15 + 30 = 15입니다.

답) 15

491

문제) 다항식 f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₂x² + a₁x + a₀ 이 정수 계수를 가지고 있으며, 그 근이 서로 다른 정수라고 가정합시다. aₙ = 2이고 a₀ = 66일 때, |aₙ₋₁|의 가능한 최소값은 얼마입니까?

풀이) f(x)가 정수 계수를 가지므로, 정수 근 정리에 따르면 f(x)의 모든 정수 근은 상수항 66 = 2·3·11을 나누어야 합니다. 따라서 f(x)의 가능한 정수 근은 ±1, ±2, ±3, ±6, ±11, ±22, ±33, ±66입니다. 또한, f(x)의 모든 근이 정수이므로, f(x)의 모든 근은 위 목록에 포함되어야 합니다. 이제 비에타의 정리를 적용합니다. f(x)의 근의 곱은 (-1)ⁿ·(a₀ / aₙ)이며, 이는 33 또는 -33입니다. 또한, 근의 합은 -aₙ₋₁ / aₙ = -aₙ₋₁ / 2입니다. 따라서 |aₙ₋₁|을 최소화하려면 근의 합의 절대값을 가능한 한 작게 만들어야 하며, 근의 곱이 33 또는 -33이어야 합니다. 두 가지 경우를 고려합니다.

경우 1: 33 또는 -33이 근인 경우, 다른 가능한 근은 ±1뿐입니다. 이 경우, 근의 합의 절대값은 최소 32입니다.

경우 2: 11 또는 -11이 근이고 3 또는 -3이 근인 경우, 다른 가능한 근은 ±1뿐입니다. 이 경우, 근의 합의 절대값은 최소 11-3-1=7이며, 이는 경우 1보다 좋습니다. 근의 합의 절대값이 7이라면, |aₙ₋₁| = 7|aₙ| = 7·2 = 14입니다.

따라서 |aₙ₋₁| ≥ 14임을 보였으며, 다음과 같이 확인할 수 있습니다. f(x) = 2(x+11)(x-3)(x-1) = 2x³ + 14x² - 82x + 66 이는 정수 계수와 정수 근을 가집니다. 따라서 |aₙ₋₁|의 가능한 최소값은 14입니다.

답) 14

492

문제) Tom은 생일 선물로 Mr. Potato Head를 받았습니다. 이 장난감에는 3가지 헤어스타일, 2세트의 눈썹, 1쌍의 구글리 눈, 2세트의 귀, 2세트의 입술, 일반 신발 한 쌍, 그리고 보너스로 광대 신발 한 쌍이 포함되어 있습니다. 완전한 Mr. Potato Head의 개성은 눈썹, 눈, 귀, 입술, 신발, 그리고 선택적으로 머리카락을 포함합니다. Mr. Potato Head는 대머리일 수도 있습니다. 참고: "섞어서 매치"할 수 없습니다. 예를 들어, 한 쌍의 왼쪽 눈썹과 다른 쌍의 오른쪽 눈썹을 사용할 수 없습니다.

풀이) 눈썹은 2가지 선택, 눈은 1가지 선택, 귀는 2가지 선택, 입술은 2가지 선택, 신발은 2가지 선택, 머리카락은 4가지 선택(3가지 헤어스타일 또는 대머리)이 있으며, 각각은 독립적으로 선택할 수 있습니다. 따라서 조합의 수는 이들의 곱으로 계산됩니다: 2 · 1 · 2 · 2 · 2 · 4 = 64.

답) 64

493

문제) 벡터 집합 v 에 대해 proj_{(2, 1)} v = (0, 0) 인 벡터는 한 직선 위에 놓입니다. 이 직선의 방정식을 "y = mx + b" 형태로 입력하세요.

풀이) 벡터 v = (x, y) 라고 하자. 투영의 공식을 사용하면, proj_{(2, 1)} v = {[v · (2, 1)] / |(2, 1)|²} (2, 1) = {(x, y) · (2, 1) / 5} (2, 1) = ((2x + y) / 5) (2, 1) = (0, 0). 따라서 2x + y / 5 = 0 즉, 2x + y = 0 입니다. 따라서 직선의 방정식은 y = -2x 입니다.

답) y = -2x

494

문제) 숫자 (√2 + √3)³는 a√2 + b√3 + c√6의 형태로 쓸 수 있습니다. 여기서 a, b, c는 정수입니다. a + b + c는 얼마입니까?

풀이) 먼저 (√2 + √3)²를 계산합니다: (√2 + √3)² = (√2 + √3)(√2 + √3) = (√2)(√2) + (√2)(√3) + (√3)(√2) + (√3)(√3) = 2 + √6 + √6 + 3 = 5 + 2√6. 이것을 √2 + √3으로 곱하면 (√2 + √3)³ = (√2 + √3)²(√2 + √3) = (5 + 2√6)(√2 + √3) = 5√2 + 5√3 + (2√6)(√2) + (2√6)(√3) = 5√2 + 5√3 + 2√12 + 2√18 = 5√2 + 5√3 + 2(2√3) + 2(3√2) = 11√2 + 9√3. 따라서, a + b + c = 20입니다. (c=0임을 주의하세요; 까다롭습니다!) 또한, 이항 정리를 사용하여 (√3 + √2)³을 전개할 수 있습니다. 이는 (√2)³ + 3(√2)²√3 + 3√2(√3)² + (√3)³이 됩니다. 이를 단순화하면 2√2 + 6√3 + 9√2 + 3√3 = 11√2 + 9√3이 되고, 다시 한 번 a + b + c = 20입니다.

답) 20

495

문제) 집합 S를 점 (a, b)로 정의하되, 0 ≤ a, b ≤ 1이고 다음 방정식 x⁴ + ax³ - bx² + ax + 1 = 0 이 적어도 하나의 실근을 갖는 경우로 한다. S의 그래프의 면적을 구하시오.

풀이) x = 0은 방정식의 해가 될 수 없음을 주목하자. 양변을 x²로 나누면, x² + ax - b + a/x + 1/x² = 0 이 된다. y = x + 1/x로 두자. 그러면 x² - yx + 1 = 0이 된다. 이 이차방정식의 판별식은 y² - 4 이므로, |y| ≥ 2일 때 x에 실근이 존재한다. 또한, y² = x² + 2 + 1/x²이므로, y² + ay - (b + 2) = 0 이 된다. 이차방정식의 근의 공식에 따르면, 근은 y = (-a ± √(a² + 4(b + 2))) / 2 이다. 먼저, 판별식 a² + 4(b + 2)는 항상 양수임을 알 수 있다. 또한, |y| ≥ 2인 y 값이 존재하려면 (a + √(a² + 4(b + 2))) / 2 ≥ 2 이어야 한다. 그러면 a + √(a² + 4(b + 2)) ≥ 4가 되고, √(a² + 4(b + 2)) ≥ 4 - a가 된다. 양변이 모두 음수가 아니므로, 양변을 제곱하여 a² + 4(b + 2) ≥ a² - 8a + 16 을 얻는다. 이는 2a + b ≥ 2로 단순화된다. 아래는 도형을 그리는 코드입니다.

unitsize(3 cm);

fill((1/2,1)--(1,0)--(1,1)--cycle,gray(0.7));
draw((0,0)--(1,0)--(1,1)--(0,1)--cycle);
draw((1/2,1)--(1,0));

label("$0$", (0,0), S);
label("$1$", (1,0), S);
label("$a$", (1,0), E);
label("$0$", (0,0), W);
label("$1$", (0,1), W);
label("$b$", (0,1), N);

따라서, S는 꼭짓점이 (1,0), (1,1), (1/2, 1)인 삼각형이며, 그 면적은 1/4이다.

답) 1/4

496

문제) 함수 f(x) = (2-x) / log(2-log(x-2))의 정의역은 무엇인가요? 여기서 log는 밑이 10인 로그 함수입니다. 답을 구간 표기법으로 표현하세요.

풀이) 내부 로그는 x - 2 > 0일 때만 정의되므로, x > 2입니다. 또한, 외부 로그는 2 - log(x-2) > 0일 때만 정의되므로, 2 > log(x-2)입니다. 이는 100 > x-2를 의미하므로, x < 102입니다. 마지막으로, log(2-log(x-2)) ≠ 0이어야 하므로, 2 - log(x-2) ≠ 1입니다. 이는 log(x-2) ≠ 1과 동등하며, 따라서 x ≠ 12입니다. 따라서, 답은 x ∈ (2,12) ∪ (12,102)입니다.

답) (2,12) ∪ (12,102)

497

문제) z = 1+i이고 w = (3z+1) / (5z+7)일 때, |w|를 구하세요.

풀이) 대입하면, w = (3(1+i)+1) / (5(1+i)+7) = (4+3i) / (12+5i)입니다. 이를 a+bi 형태로 쓰고 크기를 구할 수도 있지만, 모든 복소수 a와 b에 대해 |a/b| = |a| / |b|라는 사실을 사용하는 것이 더 쉽습니다. 분자의 크기는 √(3²+4²) = √(25) = 5이고, 분모의 크기는 √(12² + 5²) = √(169) = 13입니다. 따라서 |w| = 5 / 13입니다.

답) 5 / 13

498

문제) 한 각이 같은 팔각형은 길이가 1인 변 4개와 길이가 √2 / 2인 변 4개로 구성되어 있으며, 인접한 변은 같은 길이가 아닙니다. 이 팔각형의 넓이는 얼마입니까?

풀이) 팔각형은 변의 길이가 √2 / 2인 5개의 정사각형과 4개의 반 정사각형으로 나눌 수 있습니다. 따라서 넓이는 다음과 같습니다. (5 + 4 · 1/2) · (√2 / 2)² = 7/2. 아래는 도형을 그리는 코드입니다.

unitsize(2cm);
for (int i=0; i<4; ++i) {
for (int j=0; j<4; ++j) {
draw((i,0)--(i,3),dashed);
draw((0,j)--(3,j),dashed);
};}
draw((1,0)--(2,0)--(3,1)--(3,2)--(2,3)--(1,3)--(0,2)--(0,1)--cycle,linewidth(0.7));
for (int i=0; i<2; ++i) {
label("1",(0.5+2i,2.5),S);
label("1",(0.5+2i,0.5),N);}
label("$\frac{\sqrt{2}}{2}$",(0,1.5),E);
label("$\frac{\sqrt{2}}{2}$",(3,1.5),W);

답) 7/2

499

문제) 수열 (aₙ)이 다음과 같이 정의됩니다: aᵢ₊₁ = 1 / (1 - aᵢ) 여기서 i ≥ 1입니다. 만약 a₃ = a₁이라면, (a₉)⁹을 계산하세요.

풀이) 먼저, a₃ = a₁이라면 a₁ = a₃ = a₅ = a₇ = a₉이므로, (a₉)⁹ = (a₁)⁹입니다. 다음과 같이 계산합니다: a₂ = 1 / (1 - a₁), a₃ = 1 / (1 - a₂) = 1 / (1 - (1 / (1 - a₁))) = (1 - a₁) / (1 - a₁ - 1) = (1 - a₁) / (-a₁). 따라서 (1 - a₁) / (-a₁) = a₁이므로, 1 - a₁ = -a₁²입니다. 그러면 a₁² - a₁ + 1 = 0입니다. 양변에 a₁ + 1을 곱하면 (a₁ + 1)(a₁² - a₁ + 1) = 0이므로, a₁³ + 1 = 0입니다. 따라서 a₁³ = -1이고, a₁⁹ = (-1)³ = -1입니다.

답) -1

500

문제) 삼각형 ABC의 높이 선분 AD와 선분 BE 가 점 H에서 교차합니다. 만약 ∠BAC = 54° 이고 ∠ABC = 52° 라면, ∠AHB 는 얼마입니까?

풀이) 먼저, 도형을 그립니다: 아래는 도형을 그리는 코드입니다.

size(150); defaultpen(linewidth(0.8));
pair B = (0,0), C = (3,0), A = (1.8,2), P = foot(A,B,C), Q = foot(B,A,C),H = intersectionpoint(B--Q,A--P);
draw(A--B--C--cycle);
draw(A--P^^B--Q);
label("$A$",A,N); label("$B$",B,W); label("$C$",C,E); label("$D$",P,S); label("$E$",Q,E); label("$H$",H,NW);
draw(rightanglemark(C,P,H,3.5));
draw(rightanglemark(H,Q,C,3.5));

angle AHB = angle DHE 입니다. 사각형 CDHE에서, angle DHE = 360° - angle HEC - angle ECD - angle CDH = 360° - 90° - angle ACB - 90° = 180° - angle ACB . 삼각형 ABC에서, 180° - angle ACB = angle BAC + angle ABC = 54° + 52° = 106° 입니다.

답) 106°

입력: 2026.01.09 22:28

'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글

【수능】 2026학년도 대학수학능력시험 수학 (0)	2025.11.18
【수능】 2025학년도 대학수학능력시험 수학 (3)	2025.11.18
【수능】 2023학년도 대학수학능력시험 수학 (0)	2025.07.08
【수능】 2024학년도 대학수학능력시험 수학 (1)	2025.06.26
【논리학】 수학 논리 문제 [41~60] (1)	2025.01.21

정빈이의 공부방

최근댓글

【수학】 Math-500

'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글

티스토리툴바

【수학】 Math-500

'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글

'▶ 자연과학/▷ 일반수학' 관련 포스팅

티스토리툴바