2025학년도 대학수학능력시험 수학
추천글 : 【수학】 수학 목차
1. 다음 값은?

풀이.

2. 함수 f(x) = x3 - 8x + 7에 대하여 다음 값은?

풀이.

3. 첫째항과 공비가 모두 양수 k인 등비수열 {an}이 다음을 만족시킬 때, k의 값은?

풀이.

4. 다음과 같은 함수가 실수 전체의 집합에서 연속일 때, 상수 a의 값은?

풀이.

5. 함수 f(x) = (x2 + 1)(3x2 - x)에 대하여 f'(1)의 값은?
풀이.
f'(1) = 2x (3x2 - x) + (x2 + 1)(6x - 1) | x=1 = 2 × 2 + 2 × 5 = 14
6. cos(π/2 + θ) = -1/5일 때, sin θ / (1 - cos2 θ)의 값은?
풀이.
cos(π/2 + θ) = -sinθ = -1/5
∴ sin θ / (1 - cos2 θ) = sin θ / sin2 θ = 1 / sin θ = 5
7. 다항함수 f(x)가 모든 실수 x에 대하여 다음을 만족시킬 때, f(1)의 값은?

풀이.
f(x) = d/dx (3x3 + 2x) = 9x2 + 2
∴ f(1) = 9 + 2 = 11
8. 다음과 같은 두 실수에 대하여 a × b의 값은?

풀이.
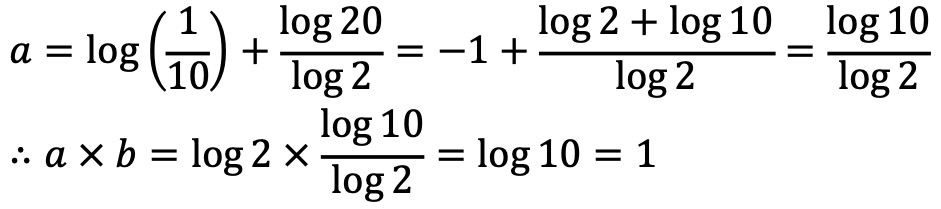
9. 함수 f(x) = 3x2 - 16x - 20에 대하여 다음과 같을 때, 양수 a의 값은?
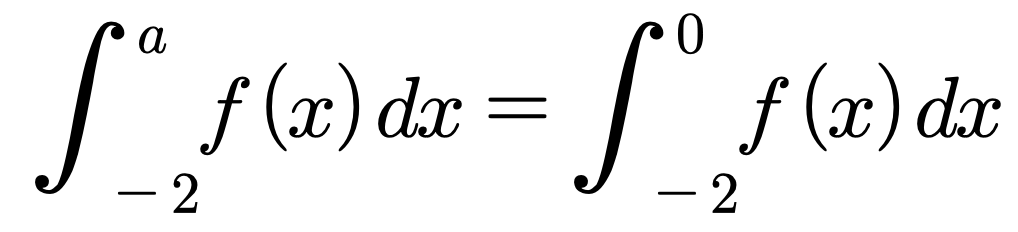
풀이.
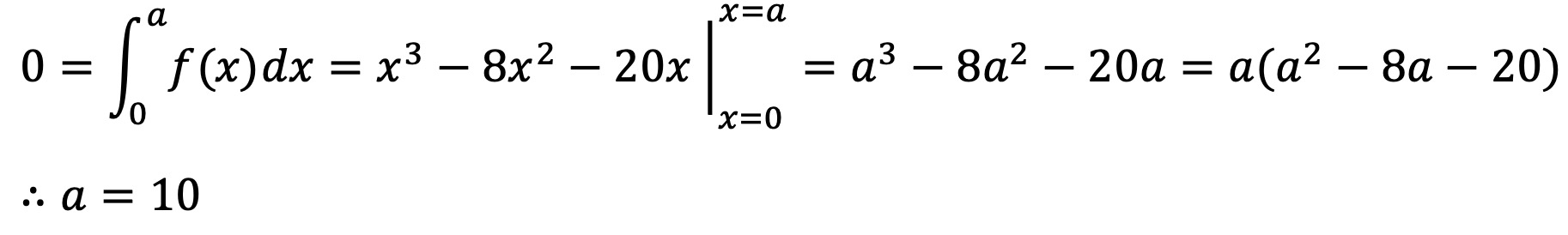
10. 닫힌구간 [0, 2π]에서 정의된 함수 f(x) = a cos(bx) + 3이 x = π / 3에서 최댓값 13을 갖도록 하는 두 자연수 a, b의 순서쌍 (a, b)에 대하여 a + b의 최솟값은?
풀이.
a + 3 = 13으로부터 a = 10을 얻는다.
1 = cos(b × π / 3) = cos(2nπ), n ∈ ℕ이므로 b = 6n을 얻는다.
그러므로 a + b = 10 + 6n ≥ 16
11. 시각 t = 0일 때 출발하여 수직선 위를 움직이는 점 P의 시각 t (t ≥ 0)에서의 위치 x가 x = t3 - (3/2)t2 - 6t이다. 출발한 후 점 P의 운동 방향이 바뀌는 시각에서의 점 P의 가속도는?
풀이.
dx/dt = 3t2 - 3t - 6 = 3(t2 - t - 2) = 3(t - 2)(t + 1) = 0 ⇔ t = 2
∴ dx2 /dt2 |t=2 = 6t - 3 |t=2 = 9
12. a1 = 2인 수열 {an}과 b1 = 2인 등차수열 {bn}이 모든 자연수 n에 대하여 다음을 만족시킬 때, a1 + a2 + a3 + a4 + a5의 값은?
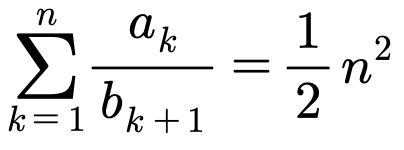
풀이.
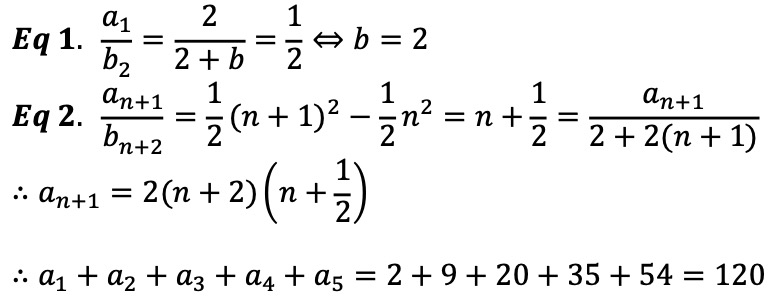
13. 최고차항의 계수가 1인 삼차함수 f(x)가 f(1) = f(2) = 0, f'(0) = -7을 만족시킨다. 원점 O와 점 P(3, f(3))에 대하여 선분 OP가 곡선 y = f(x)와 만나는 점 중 P가 아닌 점을 Q라 하자. 곡선 y = f(x)와 y축 및 선분 OQ로 둘러싸인 부분의 넓이를 A, 곡선 y = f(x)와 선분 PQ로 둘러싸인 부분의 넓이를 B라 할 때, B - A의 값은?
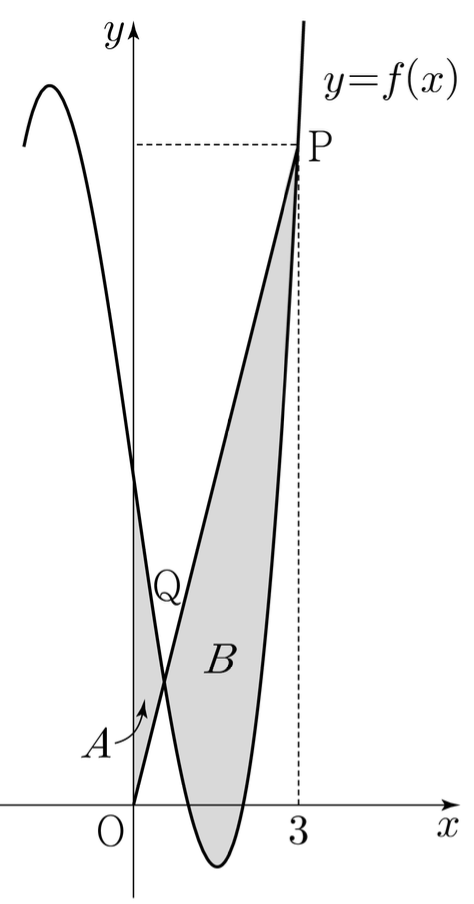
풀이.
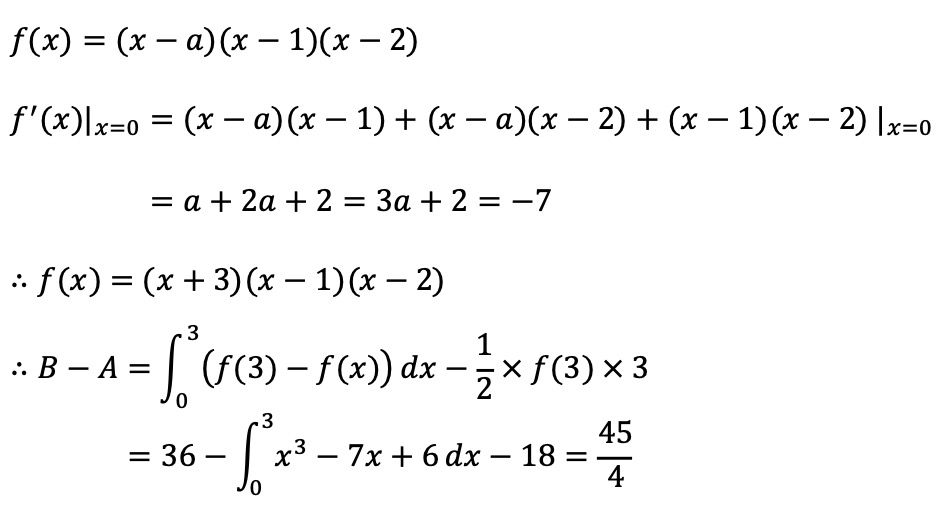
14. 그림과 같이 삼각형 ABC에서 선분 AB 위에 AD : DB = 3 : 2인 점 D를 잡고, 점 A를 중심으로 하고 점 D를 지나는 원을 O, 원 O와 선분 AC가 만나는 점을 E라 하자. sin A : sin C = 8 : 5이고, 삼각형 ADE와 삼각형 ABC의 넓이의 비가 9 : 35이다. 삼각형 ABC의 외접원의 반지름의 길이가 7일 때, 원 O 위의 점 P에 대하여 삼각형 PBC의 넓이의 최댓값은? (단, AB < AC)
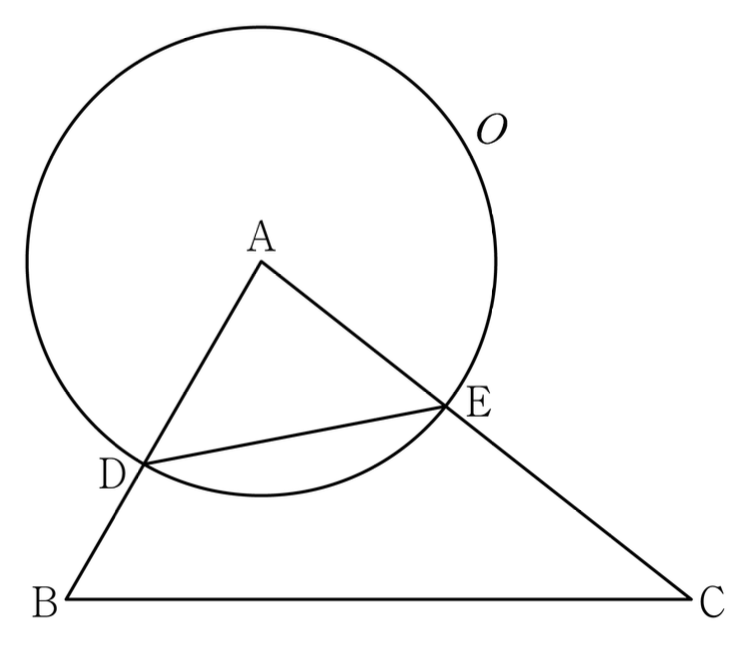
풀이.
AD = AE = 3k, DB = 2k, EC = 4k
∴ AB = c = 5k, AC = b = 7k
사인법칙에 의해 BC / sin A = AB / sin C ⇔ BC = a = 8k
헤론의 공식에 따라 △ABC = √(s(s-a)(s-b)(s-c)) = 10√3 k2 (cf. s = (a + b + c) / 2 = 10k)
또한, 외접원 반지름을 이용하여 △ABC = (1/2) ab sin C = (1/2) ab × c/2R = abc / 4R = 280k3 / 28 = 10k3
∴ 10√3 k2 = 10k3으로부터 k = √3을 얻을 수 있다.
A에서 BC까지의 거리 = 2△ABC / BC = 2 × 30√3 / 8√3 = 7.5
∴ △PBC = (1/2) × BC × (A에서 BC까지의 거리 + 추가 거리) ≤ (1/2) × BC × (7.5 + AD) = (1/2) × 8√3 × (7.5 + 3√3) = 36 + 30√3
15. 상수 a (a ≠ 3√5)와 최고차항의 계수가 음수인 이차함수 f(x)에 대해 함수
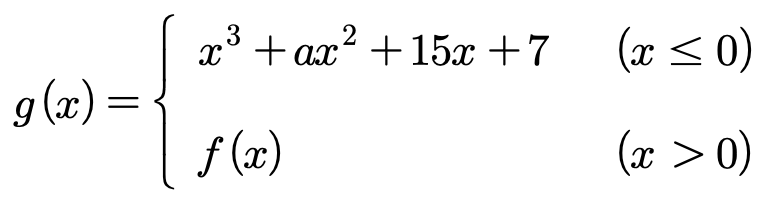
가 다음 조건을 만족시킨다.
㈎ 함수 g(x)는 실수 전체의 집합에서 미분가능하다.
㈏ x에 대한 방정식 g'(x) × g'(x-4) = 0의 서로 다른 실근의 개수는 4이다.
g(-2) + g(2)의 값은?
풀이.
a ≠ 3√5이므로 g'(x) = 0이 x ≤ 0에서 중근을 갖지 않는다.
g'(x) = 3x2 + 2ax + 15에 x = 0을 대입하면 15 = g'(0) = f'(0)을 얻을 수 있다.
f'(x)는 일차함수이고 최고차항의 계수가 음수이므로 f'(x) = 0인 x > 1이 정확하게 1개 존재한다.
g'(x) = 0인 x ≤ 0이 존재하지 않으면, g'(x) × g'(x-4) = 0의 서로 다른 실근의 개수가 4개가 되기에는 부족하다.
그런데 g'(x) = 0, x ≤ 0이 중근을 갖지 않으므로 g'(x) = 0은 x ≤ 0에서 2개, x > 0에서 1개의 해를 갖는다.
이를 차례대로 x1 < x2 < x3라고 하면, g'(x-4) = 0은 x2 < x3 < x4를 해로 갖는다.
이때 x2, x3는 이차함수에 의한 해이고, x4는 일차함수(즉, f'(x-4))에 의한 해이다.
따라서 g'(x) = 3x2 + 2ax + 15 = 3(x-t)(x-t-4)와 같은 형태이다.
이때 (t, a) = (-5, 9), (1, -9)와 같이 정해지고, x1 + x2 = -2a / 3 < 0이므로 a = 9이다.
한편, x3 = x2 + 4 = (-5 + 4) + 4 = 3이므로 f'(x) = 15 - 5x ⇔ f(x) = 7 + 15x - 2.5x2을 얻는다.
따라서, g(-2) + g(2) = (-8 + 36 -30 + 7) + (7 + 30 - 10) = 5 + 27 = 32
16. 방정식 log2(x - 3) = log4(3x - 5)를 만족시키는 실수 x의 값을 구하시오.
풀이.
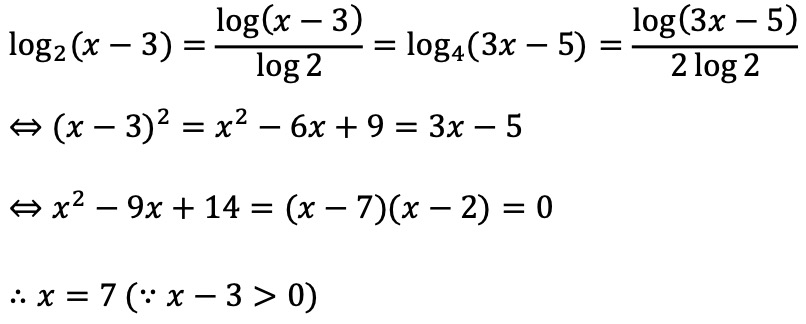
17. 다항함수 f(x)에 대하여 f'(x) = 9x2 + 4x이고 f(1) = 6일 때, f(2)의 값을 구하시오.
풀이.
f(x) = 3x3 + 2x2 + C = 3x3 + 2x2 + 1 (∵ f(1) = 6)
∴ f(2) = 24 + 8 + 1 = 33
18. 수열 {an}이 모든 자연수 n에 대하여 an + an+4 = 12를 만족시킬 때, a1 + a2 + ⋯ + a16의 값을 구하시오.
풀이.
a1 + a2 + ⋯ + a16 = ((a1 + a5) + ⋯ + (a4 + a8)) + ((a9 + a13) + ⋯ + (a12 + a16)) = (12 + ⋯ + 12) + (12 + ⋯ + 12) = 96
19. 양수 a에 대하여 함수 f(x)를 f(x) = 2x3 - 3ax2 - 12a2x라 하자. 함수 f(x)의 극댓값이 7/27일 때, f(3)의 값을 구하시오.
풀이.
f'(x) = 6x2 - 6ax - 12a2 = 6(x2 - ax - 2a2) = 6(x-2a)(x+a)
x = -a에서의 함숫값이 극댓값이므로 f(-a) = -2a3 - 3a3 + 12a3 = 7a3 = 7/27 ⇔ a = 1/3
∴ f(3) = 54 - 9 - 4 = 41
20. 곡선 y = (1/5)x-3과 직선 y = x가 만나는 점의 x좌표를 k라 하자. 실수 전체의 집합에서 정의된 함수 f(x)가 다음 조건을 만족시킨다.
x > k인 모든 실수 x에 대하여 f(x) = (1/5)x-3이고 f(f(x)) = 3x이다.
f(1 / (k3 × 53k))의 값을 구하시오.
풀이.
x > k의 경우 f(x) = (1/5)x-3 < f(k) = k이므로, x' < k의 경우 f(x') = f(f(x)) = 3x = 3f-1(x') = -3 ln(x'/125) / ln5가 성립한다.
이때 2 < k < 3임은 쉽게 확인할 수 있으므로, 1 / (k3 × 53k) < k이다.
따라서 f(1 / (k3 × 53k))의 값은 다음과 같다.
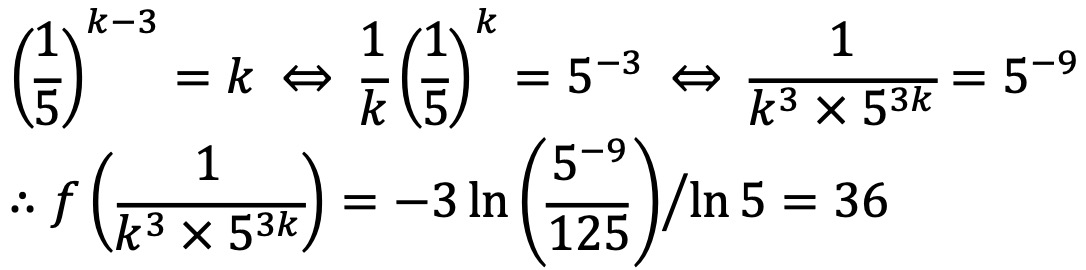
21. 함수 f(x) = x3 + ax2 + bx + 4가 다음 조건을 만족시키도록 하는 두 정수 a, b에 대해 f(1)의 최댓값을 구하시오.
모든 실수 α에 대하여 limx→α f(2x+1) / f(x)의 값이 존재한다.
풀이.
f(x)는 3차 함수이므로 세 개의 실근을 갖거나 1개의 실근과 2개의 허수근을 갖는다.
f(x)의 실근 1개를 α로 두면 f(2x+1) / f(x)가 수렴하기 위해 f(2α+1)도 실근이어야 한다.
2α+1를 α'으로 두면 f(2x+1) / f(x)가 수렴하기 위해 f(2α'+1)도 실근이어야 한다.
따라서 f(x)는 α, 2α+1, 2(2α+1)+1, ···을 근으로 가져야 하므로 α ≠ -1이라면 무한히 많은 근을 가지게 되어 모순이다.
f(-1) = a - b + 3 = 0이므로 f(x) = (x+1)(x2 + (a-1)x + 4)에서 2차식의 판별식 D = (a-1)2 - 16 < 0 ⇔ -3 < a < 5를 얻는다.
그러므로 f(1) = 5 + a + b = 8 + 2a ≤ 8 + 8 = 16로부터 f(1)의 최댓값은 16이다.
22. 모든 항이 정수이고 다음 조건을 만족시키는 모든 수열 {an}에 대하여 |a1|의 값의 합을 구하시오.
㈎ 모든 자연수 n에 대하여 다음이 성립한다.

㈏ |am| = |am+2|인 자연수 m의 최솟값은 3이다.
풀이.
a1이 너무 크면 첫 몇 개에 대하여는 a1 > a2 > a3 > ··· 순으로 계속 크기가 작아질 것이다.
따라서, 넉넉히 잡아 a1 = -100 ~ 100일 때 a3 = a5인지 살피면 |a1|의 후보를 쉽게 구할 수 있다.
이 문제의 취지는 a1 = -10 ~ 10에서의 경우를 살펴 수열의 패턴을 파악하고 적절히 일반화하는 것으로 판단된다.
| a1 | a2 | a3 | a4 | a5 |
| -10 | -5 | -8 | -4 | -2 |
| -9 | -12 | -6 | -3 | -6 |
| -8 | -4 | -2 | -1 | -4 |
| -7 | -10 | -5 | -8 | -4 |
| -6 | -3 | -6 | -3 | -6 |
| -5 | -8 | -4 | -2 | -1 |
| -4 | -2 | -1 | -4 | -2 |
| -3 | -6 | -3 | -6 | -3 |
| -2 | -1 | -4 | -2 | -1 |
| -1 | -4 | -2 | -1 | -4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | -2 | -1 | -4 | -2 |
| 2 | 1 | -2 | -1 | -4 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 2 | 1 | -2 | -1 |
| 5 | 2 | 1 | -2 | -1 |
| 6 | 3 | 0 | 0 | 0 |
| 7 | 4 | 2 | 1 | -2 |
| 8 | 4 | 2 | 1 | -2 |
| 9 | 6 | 3 | 0 | 0 |
| 10 | 5 | 2 | 1 | -2 |
우선, a3 = 2, a5 = -2가 되도록 하는 a1은 a1 = 7, 8, 10이며, 그 이후는 숫자가 커서 a3 > a4 > a5이 성립한다.
또한, a3 = a5 = 0이 되도록 하는 a1은 a1 = 6이며, 그 이후는 숫자가 커서 a3 > a4 > a5이 성립한다.
마지막으로, a3 = a5 = -6이 되도록 하는 a1은 a1 = -9, -24이다.
-24를 찾는 것은 수학적 센스를 많이 요구할 것으로 보인다.
따라서, ∑i |a1,i| = (7 + 8 + 10) + 6 + (9 + 24) = 64
(확률과 통계) 23. 다항식 (x3 + 2)5의 전개식에서 x6의 계수는?
풀이.
5C2 × 25-2 = 80
(확률과 통계) 24. 두 사건 A, B에 대하여 P(A | B) = P(A) = 1/2, P(A ∩ B) = 1/5일 때, P(A ∪ B)의 값은?
풀이.
1/5 = P(A ∩ B) = P(A) × P(B) = 1/2 × P(B)
∴ P(B) = 2/5
∴ P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 1/2 + 2/5 - 1/5 = 7/10 (∵ 포함배제의 원리)
(확률과 통계) 25. 정규분포 N(m, 22)을 따르는 모집단에서 크기가 256인 표본을 임의추출하여 얻은 표본평균을 이용하여 구한 m에 대한 신뢰도 95%의 신뢰구간이 a ≤ m ≤ b이다. b - a의 값은? (단, Z가 표준정규분포를 따르는 확률변수일 때, P(|Z| ≤ 1.96) = 0.95로 계산한다.)
풀이.
1.96 = (b - m) / (2 / 16) ⇔ b = 3.84 / 16 + m
∴ b - a = 2(b - m) = 2 × 3.84 / 16 = 0.48
(확률과 통계) 26. 어느 학급의 학생 16명을 대상으로 과목 A와 과목 B에 대한 선호도를 조사하였다. 이 조사에 참여한 학생은 과목 A와 과목 B 중 하나를 선택하였고, 과목 A를 선택한 학생은 9명, 과목 B를 선택한 학생은 7명이다. 이 조사에 참여한 학생 16명 중에서 임의로 3명을 선택할 때, 선택한 3명의 학생 중에서 적어도 한 명이 과목 B를 선택한 학생일 확률은?
풀이.
(준식) = 1 - P(3명 모두 A를 선택할 확률) = 1 - 9C3 / 16C3 = 1 - 84 / 560 = 17/20
(확률과 통계) 27. 숫자 1, 3, 5, 7, 9가 각각 하나씩 적혀 있는 5장의 카드가 들어 있는 주머니가 있다. 이 주머니에서 임의로 1장의 카드를 꺼내어 카드에 적혀 있는 수를 확인한 후 다시 넣는 시행을 한다. 이 시행을 3번 반복하여 확인한 세 개의 수의 평균을 X̄라 하자. V(aX̄ + 6) = 24일 때, 양수 a의 값은?
풀이.
V(aX̄ + 6) = a2 V(X̄) = a2 V((X1 + X2 + X3) / 3) = (a2/9) × 3 × V(X1) = (a2/3) × (1/5) × ((-4)2 + (-2)2 + 22 + 42) = 24
⇔ a = 3
(확률과 통계) 28. 집합 X = {1, 2, 3, 4, 5, 6}에 대하여 다음 조건을 만족시키는 함수 f : X → X의 개수는?
㈎ f(1) × f(6)의 값이 6의 약수이다.
㈏ 2f(1) ≤ f(2) ≤ f(3) ≤ f(4) ≤ f(5) ≤ 2f(6)
풀이.
다음과 같은 각 경우에 대해 쉽게 경우의 수를 셀 수 있다.
● 경우 1. (f(1), f(6)) = (1, 1) : 경우의 수 = 1
● 경우 2. (f(1), f(6)) = (1, 2) : 경우의 수 = 15
● 경우 3. (f(1), f(6)) = (1, 3) : 경우의 수 = 70
● 경우 4. (f(1), f(6)) = (1, 6) : 경우 3과 같은 70개
● 경우 5. (f(1), f(6)) = (2, 3) : 경우 2와 같은 15개
따라서 총 171개
(확률과 통계) 29. 정규분포 N(m1, σ12)을 따르는 확률변수 X와 정규분포 N(m2, σ22)을 따르는 확률변수 Y가 다음 조건을 만족시킨다.
모든 실수 x에 대하여 P(X ≤ x) = P(X ≥ 40 - x)이고 P(Y ≤ x) = P(X ≤ x + 10)이다.
P(15 ≤ X ≤ 20) + P(15 ≤ Y ≤ 20)의 값을 오른쪽 표준정규분포표를 이용하여 구한 것이 0.4772일 때, m1 + σ2의 값을 구하시오. (단, σ1과 σ2는 양수이다.)
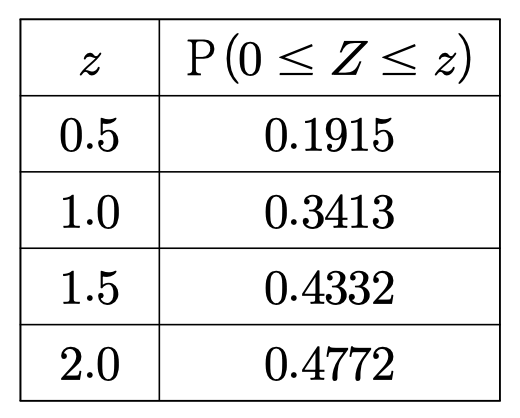
풀이.
P(X ≤ x) = P(X ≥ 40 - x)로부터 m1 = 40/2 = 20을 얻고, P(Y ≤ x) = P(X ≤ x + 10)로부터 m2 = m1 + 10 = 30을 얻는다.
P(15 ≤ X ≤ 20) + P(15 ≤ Y ≤ 20) = P(15 ≤ X ≤ 20) + P(25 ≤ X ≤ 30) = P(20 ≤ X ≤ 25) + P(25 ≤ X ≤ 30) = P(20 ≤ X ≤ 30)
따라서, 0.4772 = P(0 ≤ Z ≤ 2.0) = P(20 ≤ σ1Z + 20 = X ≤ 2σ1 + 20) = P(20 ≤ X ≤ 30) ⇔ σ1 = 5
m1 + σ2 = m1 + σ1 = 25
(확률과 통계) 30. 탁자 위에 5개의 동전이 일렬로 놓여 있다. 이 5개의 동전 중 1번째 자리와 2번째 자리의 동전은 앞면이 보이도록 놓여 있고, 나머지 자리의 3개의 동전은 뒷면이 보이도록 놓여 있다. 이 5개의 동전과 한 개의 주사위를 사용하여 다음 시행을 한다.
주사위를 한 번 던져 나온 눈의 수가 k일 때, k ≤ 5이면 k번째 자리의 동전을 한 번 뒤집어 제자리에 놓고, k = 6이면 모든 동전을 한 번씩 뒤집어 제자리에 놓는다.
위의 시행을 3번 반복한 후 이 5개의 동전이 모두 앞면이 보이도록 놓여 있을 확률은 q / p이다. p + q의 값을 구하시오. (단, p와 q는 서로소인 자연수이다.)
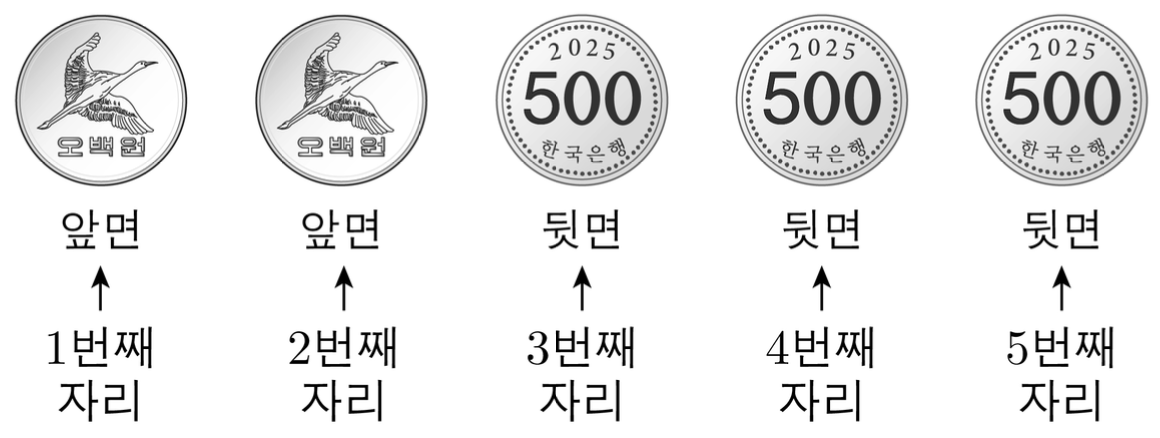
풀이.
경우 1. 1개의 동전을 뒤집는 행위를 3번 한 확률 = (1/6)3 × 3! = 1/36
경우 2. 1개의 동전을 뒤집는 행위를 2번 하고 나서 모든 동전을 한 번씩 뒤집는 행위를 1번 한 확률 = (1/6)2 × 2! × (1/6) = 1/108
경우 3. 모든 동전을 한 번씩 뒤집는 행위를 1번 하고 나서 1개의 동전을 뒤집는 행위를 2번 한 확률 = (1/6) × (1/6)2 × 2! = 1/108
경우 4. 1개의 동전을 뒤집는 행위를 1번 하고 나서 모든 동전을 한 번씩 뒤집고 다시 1개의 동전을 뒤집는 확률 = 1/108
∴ 1/36 + 3/108 = 1/18 = q / p ⇔ p + q = 19
(미적분) 23. 다음 값은?
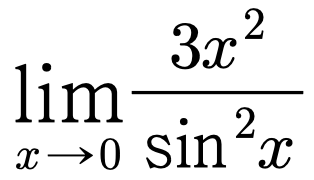
풀이.
답은 3. x → 0에서 sin x ≈ x이다.
입력: 2025.02.06 11:22
'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글
| 【논리학】 수학 논리 문제 [41~60] (1) | 2025.01.21 |
|---|---|
| 【논리학】 수학 논리 문제 [21~40] (7) | 2023.10.12 |
| 【논리학】 수학 논리 문제 [01~20] (13) | 2023.09.09 |
| 【논리학】 더지니어스 전략윷놀이 복기 (최연승 vs 임요한) (0) | 2018.02.15 |
| 【논리학】 더지니어스 전략윷놀이 복기 (성규 vs 차민수) (0) | 2018.02.15 |




최근댓글