수학 논리 문제 [41~60]
추천글 : 【수학】 수학 목차
문제 41. (PSAT) 다음 글의 내용이 참일 때, 반드시 참인 것은?
호텔 A에서 살인 사건이 발생했고, 손님 중에 범인(들)이 있다. 이 사건에 대하여 갑, 을, 병 세 사람이 각각 다음과 같이 두 개씩 진술을 했다. 이 세 사람 중 한 사람의 진술은 모두 참이고 다른 한 사람의 진술은 모두 거짓이며, 또 다른 한 사람의 진술은 하나는 참이고 다른 하나는 거짓이다.
갑 : 이 사건의 범인은 단독범이고, 그는 이 호텔의 2층에 묵고 있다. 이 호텔 2층의 방은 모두 손님이 투숙하고 있어 2층에는 빈 방이 없다.
을 : 이 사건이 단독범의 소행이라면, 그 범인은 이 호텔의 5층에 투숙하고 있다. 이 사건의 범인은 단독범이 아니고 그들은 같은 방에 투숙하고 있지도 않다.
병 : 이 사건이 단독범의 소행이 아니라면, 범인들은 같은 방에 투숙하고 있다. 이 호텔의 모든 방은 손님이 투숙하고 있어 빈 방이 없다.
1. 갑의 진술은 둘 다 거짓일 수 있다.
2. 2층에는 빈 방이 없지만, 다른 층에는 빈 방이 있다.
3. 병의 진술이 둘 다 거짓이라면, 갑의 진술 중 하나는 거짓이다.
4. 을의 진술이 둘 다 거짓이라면, 이 사건은 단독범의 소행이 아니다.
5. 갑의 진술 중 하나만 참이라면, 이 사건의 범인은 단독범이 아니다.
풀이 41. 답은 3번
○ 1. 갑의 진술이 둘 다 거짓이라고 가정하자. 범인은 단독범이 아니거나 2층에 묵고 있지 않다. 그리고 2층에는 빈 방이 있다. 을의 첫 번째 진술은 참이다. 병의 두 번째 진술은 거짓이다. 그러므로 하나는 진실, 하나는 거짓인 진술을 하는 병의 첫 번째 진술에 따라, 이 사건이 단독범의 소행이 아니라면, 범인들은 같은 방에 투숙하고 있다. 모두 진실을 진술하는 을의 두 번째 진술에 의해 범인은 단독범이 아니고 같은 방에 투숙하고 있지 않다. ◼︎과 ◼︎는 서로 모순이다.
○ 2. 빈 방이 없고, 범인이 단독범이며, 가령 그는 3층에 묵고 있다고 가정하자. 갑의 첫 번째 진술은 거짓이고, 두 번째 진술은 참이다. 을의 두 진술은 모두 거짓이다. 병의 첫 번째 진술은 거짓인 명제를 전제로 하므로 참이고, 두 번째 진술은 참이다. 그러므로 반례가 존재하므로 2번 명제가 반드시 참이라고 할 수 없다.
○ 3. 병의 진술이 둘 다 거짓이라고 가정하자. 이 사건이 단독범의 소행이거나 범인들은 같은 방에 투숙하고 있지 않다. 또한, 이 호텔에 빈 방이 있다. 이때 갑의 모두 진술이 참이라면 을의 두 진술이 모두 거짓이 되어 모순이다. 그러므로 갑의 진술 중 하나는 거짓이다.
○ 4. 을의 진술이 둘 다 거짓이라고 가정하자. 이 사건이 공범의 소행이면 공범은 같은 방에 투숙하고 있고, 단독범의 소행이면 그 범인은 5층에 투숙하고 있지 않다. 이 사건이 단독범의 소행이고, 가령 그는 3층에 묵고 있으며, 빈 방이 없다고 가정하자. 갑의 첫 번째 진술은 거짓이고, 두 번째 진술은 참이다. 병의 첫 번째 진술은 거짓인 명제를 전제로 하므로 참이고, 두 번째 진술은 참이다. 그러므로 단독범의 소행이 아니라고 단정할 수 없다.
○ 5. 가령, 이 사건의 범인은 단독범이고, 그는 이 호텔의 3층에 묵고 있으며, 호텔에 빈 방이 없다고 가정하자. 갑의 첫 번째 진술은 거짓이고, 두 번째 진술은 참이다. 을의 두 진술은 모두 거짓이다. 병의 첫 번째 진술은 거짓인 명제를 전제로 하므로 참이고, 두 번째 진술은 참이다. 그러므로 5번 명제가 반드시 참이라고 할 수 없다.
문제 42. (PSAT) 다음 글의 내용이 참일 때, 반드시 참이라고 할 수 없는 것은?
직원 갑, 을, 병, 정, 무를 대상으로 A, B, C, D 네 개 영역에 대해 최우수, 우수, 보통 가운데 하나로 분류하는 업무 평가를 실시하였다. 그리고 그 결과는 다음과 같았다.
* 모든 영역에서 보통 평가를 받은 직원이 있다.
* 모든 직원이 보통 평가를 받은 영역이 있다.
* D 영역에서 우수 평가를 받은 직원은 모두 A 영역에서도 우수 평가를 받았다.
* 갑은 C 영역에서만 보통 평가를 받았다.
* 을만 D 영역에서 보통 평가를 받았다.
* 병, 정은 A, B 두 영역에서 최우수 평가를 받았고 다른 직원들은 A, B 어디서도 최우수 평가를 받지 않았다.
* 무는 1개 영역에서만 최우수 평가를 받았다.
1. 갑은 A 영역에서 우수 평가를 받았다.
2. 을은 B 영역에서 보통 평가를 받았다.
3. 병은 C 영역에서 보통 평가를 받았다.
4. 정은 D 영역에서 최우수 평가를 받았다.
5. 무는 A 영역에서 우수 평가를 받았다.
풀이 42. 답은 5번
○ D 영역에서 우수 평가를 받은 직원의 "존재성"을 가정해야 함
○ 다음은 알아낸 순서대로 ⑴, ⑵, ⑶, ···을 부여하여 나타냄
| A | B | C | D | |
| 갑 | 우수 ⑼ | 우수 ⑷ | 보통 ⑴ | 우수 ⑼ |
| 을 | 보통 ⑻ | 보통 ⑻ | 보통 ⑸ | 보통 ⑵ |
| 병 | 최우수 ⑶ | 최우수 ⑶ | 보통 ⑸ | 최우수 ⑹ |
| 정 | 최우수 ⑶ | 최우수 ⑶ | 보통 ⑸ | 최우수 ⑹ |
| 무 | 최우수 아님 | 최우수 아님 | 보통 ⑸ | 최우수 ⑺ |
문제 43. (PSAT) 다음 대화의 ㉠에 들어갈 말로 가장 적절한 것은?
서의 : 이번에 사내 연수원에 개설된 과목인 경제, 법률, 철학, 행정에 대한 수강신청결과가 나왔는데, 경제를 신청한 사람은 모두 법률도 신청했다고 해.
승민 : 그래? 나도 그 결과를 보았는데, 행정을 신청한 사람 중에 법률을 신청한 사람은 아무도 없었어. 그리고 경제와 법률은 신청하지 않고 철학은 신청한 사람도 있었다더군.
승범 : 나도 그 결과에 대해 몇 가지 얘기를 들었는데, 법률을 신청한 사람 중에 철학을 신청한 사람도 있었대. 그리고 철학은 신청했으나 행정과 경제는 신청하지 않은 사람도 있었다는 거야.
승민 : 그런데 ( ㉠ )
서의 : 정말? 그러면 철학 한 과목만 신청한 사람이 적어도 한 명은 있겠구나.
승범 : 맞아. 그리고 적어도 한 명은 행정만 빼고 나머지 세 과목 전부 신청했다는 것도 알 수 있어.
1. 경제와 법률 두 과목만을 신청한 사람은 한 명도 없어.
2. 행정과 철학 두 과목만을 신청한 사람은 한 명도 없어.
3. 법률과 철학 두 과목만을 신청한 사람은 한 명도 없어.
4. 경제와 법률을 둘 다 신청한 사람은 모두 철학을 신청했어.
5. 법률과 철학을 둘 다 신청한 사람 중에 행정을 신청한 사람은 없어.
풀이 43. 답은 3번
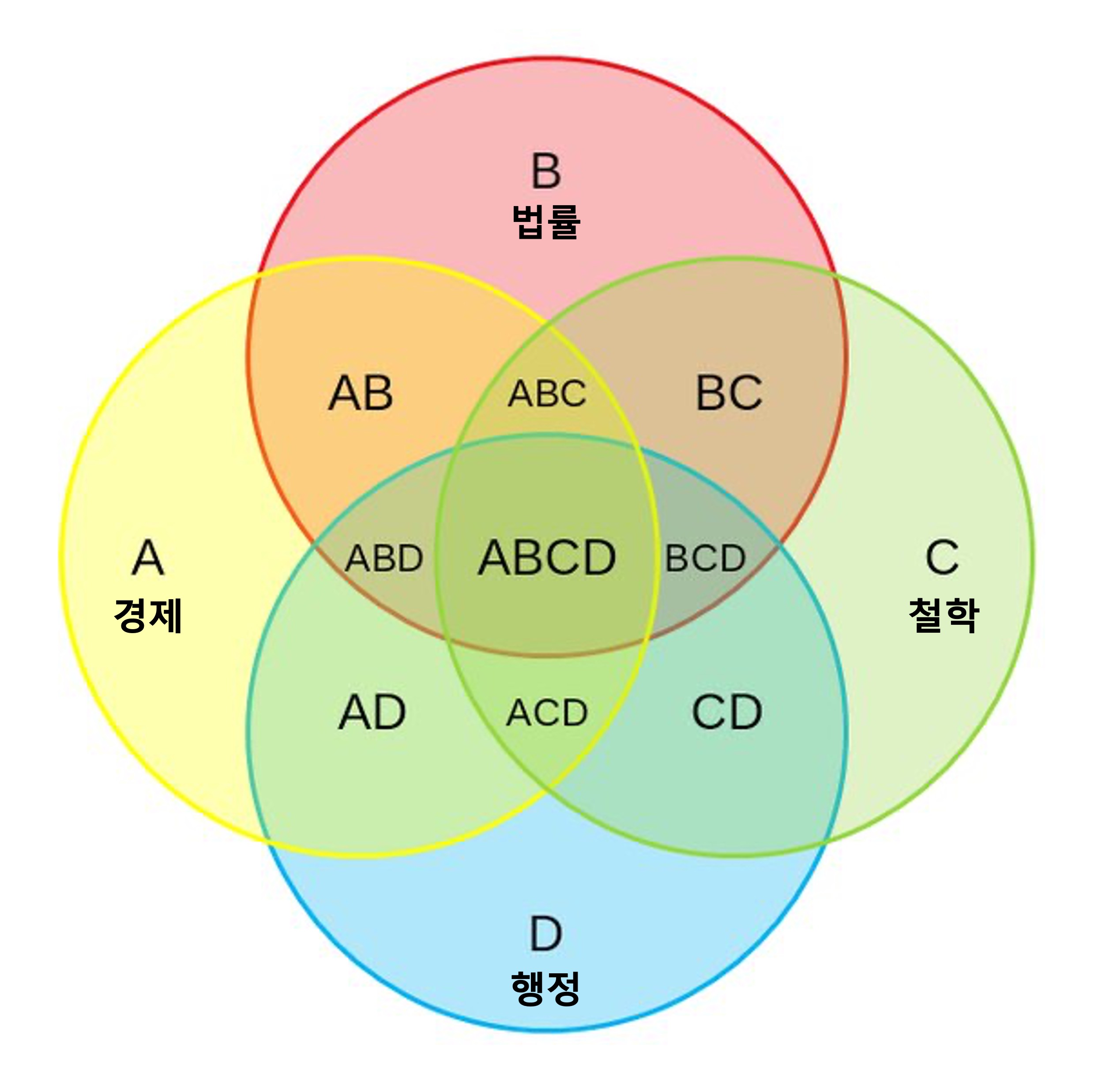
○ 경제 ⊂ 법률 ⇔ A = AD = ACD = ∅
○ 행정 ∩ 법률 = ∅ ⇔ ABD = ABCD = BCD = ∅
○ 철학 - 경제 - 법률 ≠ ∅ ⇔ C + CD ≠ ∅
○ 법률 ∩ 철학 ≠ ∅ ⇔ ABC + BC ≠ ∅
○ 철학 - 행정 - 경제 ≠ ∅ ⇔ C + BC ≠ ∅
○ 따라서 ㉠을 통해 C ≠ ∅, ABC ≠ ∅가 도출되어야 함
○ 그러므로 BC = ∅이면 위 결론이 깔끔하게 도출됨
문제 44. 다음 진술이 모두 참일 때 반드시 참인 것은? (ref)
오 주무관이 회의에 참석하면, 박 주무관도 참석한다.
박 주무관이 회의에 참석하면, 홍 주무관도 참석한다.
홍 주무관이 회의에 참석하지 않으면, 공 주무관도 참석하지 않는다.
① 공 주무관이 회의에 참석하면, 박 주무관도 참석한다.
② 오 주무관이 회의에 참석하면, 홍 주무관은 참석하지 않는다.
③ 박 주무관이 회의에 참석하지 않으면, 공 주무관은 참석한다.
④ 홍 주무관이 회의에 참석하지 않으면, 오 주무관도 참석하지 않는다.
풀이 44. 답은 ④
○ 오 주무관 ⊂ 박 주무관
○ 박 주무관 ⊂ 홍 주무관
○ ~홍 주무관 ⊂ ~공 주무관 ⇔ 공 주무관 ⊂ 홍 주무관
①, ③ 공 주무관과 박 주무관은 그저 홍 주무관의 두 부분집합에 불과함 (×)
② 오 주무관 ⊂ 홍 주무관이 성립하므로, 오 주무관 ⊄ 홍 주무관이 성립함 (×)
④ ~ 홍 주무관 ⊂ ~ 오 주무관 ⇔ 오 주무관 ⊂ 홍 주무관이므로 참 (○)
문제 45. 더지니어스 전략 윷놀이
풀이 45.
입력: 2025.01.18 22:25
'▶ 자연과학 > ▷ 일반수학' 카테고리의 다른 글
| 【수능】 2025학년도 대학수학능력시험 수학 (3) | 2025.02.07 |
|---|---|
| 【논리학】 수학 논리 문제 [21~40] (7) | 2023.10.12 |
| 【논리학】 수학 논리 문제 [01~20] (13) | 2023.09.09 |
| 【논리학】 더지니어스 전략윷놀이 복기 (최연승 vs 임요한) (0) | 2018.02.15 |
| 【논리학】 더지니어스 전략윷놀이 복기 (성규 vs 차민수) (0) | 2018.02.15 |




최근댓글