추천글 : 【자동제어】 자동제어 5급 문제풀이
Q. 그림과 같은 인공위성 자세제어 시스템이 있다. Fc는 gas jet에 의해 발생하는 힘이고, Md는 외란(disturbance) 모멘트이며, d는 모멘트 암(arm)이다. 인공위성의 관성모멘트(Moment of Inertia)를 I로 가정하자. Gas jet에 의한 힘 Fc는 제어입력 u(t)에 의해

과 같이 결정된다. 물음에 답하시오.
Q1. 이 시스템의 운동 방정식을 구하시오.
A1. Fc와 Md는 θ를 증가시키는 방향으로 작용한다.

Q2. 위성의 자세 θ(t)를 출력(output) y(t)라 할 때, 이 시스템의 입력 u(t), 외란 Md(t), 출력 y(t)와의 관계를 블록선도(block diagram)로 표시하시오.
A2. 다음과 같은 블록선도를 그릴 수 있다.
Q3. 출력 피드백 제어 시스템에서 기준 입력(reference input) r(t) = θr(t)이고, 오차 e(t) = r(t) - y(t)이며, 제어기 전달 함수를
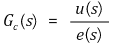
라 할 때, 출력 피드백 시스템의 블록선도를 그리시오.
A3. u(s) = Gc(s) e(s)를 이용한다.
Q4. 제어기로 비례제어기(proportional controller)를 사용하는 경우의 제어성능을 근궤적을 이용하여 설명하시오.
A4.
우선 y(s)의 표현을 얻자.
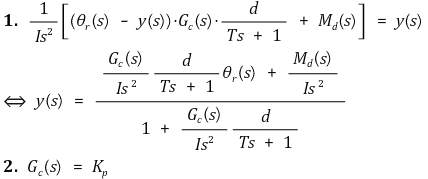
특성방정식은 전달함수의 분모가 0이 되는 극점에 대한 방정식으로 다음과 같이 주어진다.
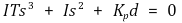
Routh-Hurwitz criterion을 통해 제어시스템이 안정하기 위한 조건을 구하자. (아래 표에서 첫 열에 sign change가 없어야 함)
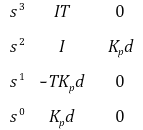
위 제어시스템이 안정하기 위해서는 -TKpd > 0이고 Kpd > 0이어야 한다.
그러나 T > 0, Kp > 0, d > 0이기 때문에 위 제어시스템은 항상 불안정하다. (등호가 없기 때문에 임계안정도 아님)
Q5. 제어기로 비례-미분 제어기(proportional-derivative controller) Gc(s) = Kp + Kd · s를 사용하는 경우, 제어시스템이 안정하기 위한 조건을 근궤적을 이용하여 구하시오. (단, Kp, Kd는 양수)
A5.
특성방정식은 다음과 같다.
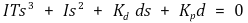
Routh-Hurwitz criterion을 통해 제어시스템이 안정하기 위한 조건을 구하자. (아래 표에서 첫 열에 sign change가 없어야 함)
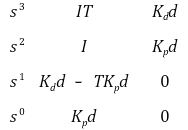
따라서 다음 조건을 얻는다.
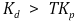
입력: 2020.05.04 16:46
'▶ 자연과학 > ▷ 5급 기술고시 풀이' 카테고리의 다른 글
| 【자동제어】 2019 국가공무원 5급(기술) 제3문 (0) | 2020.06.24 |
|---|---|
| 【자동제어】 2019 국가공무원 5급(기술) 제2문 (0) | 2020.06.24 |
| 【환경화학】 2008 국가공무원 5급(기술) 제3문 (7) | 2020.03.24 |
| 【환경화학】 2008 국가공무원 5급(기술) 제4문 (4) | 2020.02.18 |
| 【환경화학】 2006 국가공무원 5급(기술) 제5문 (5) | 2020.01.29 |





최근댓글