정수론 기초 문제 [01~20]
추천글 : 【수학】 수학 목차
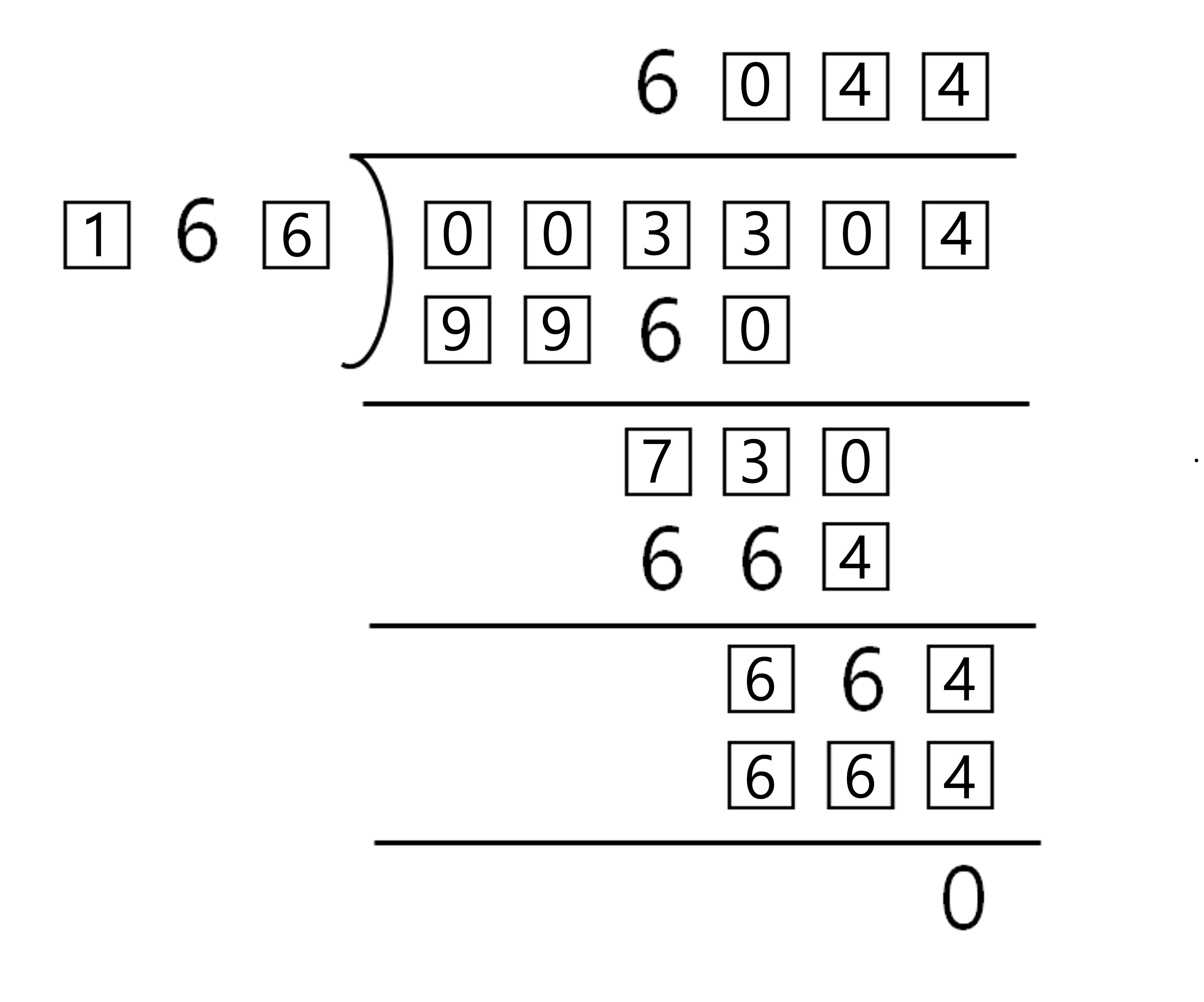
문제 1. 다음 복면산 문제에서 빈 칸을 모두 채워라.

풀이 1.
○ 먼저 알아낸 순서대로 사실을 아래와 같이 나열함
○ 사실 1. ㅁ6ㅁ × 6ㅁㅁㅁ = ㅁㅁㅁㅁㅁㅁ에서 나눗셈의 구조로 보아 6ㅁㅁㅁ의 백의 자리 수가 0임을 알 수 있음
○ 사실 2. ㅁ6ㅁ × 6 = ㅁㅁ6이라는 점에서 (cf. ㅁㅁ6ㅁ이라는 표시는 함정인 것으로 보임), ㅁ6ㅁ의 일의 자리 수가 1 or 6임을 알 수 있음
○ 사실 3. ㅁ6ㅁ × 6 = ㅁㅁ6이라는 점에서 (cf. ㅁㅁ6ㅁ이라는 표시는 함정인 것으로 보임), ㅁ6ㅁ의 백의 자리 수가 1임을 알 수 있음
○ ㅁ6ㅁ의 백의 자리 수가 0이라면, ㅁ6ㅁ (= 061 or 066) × ㅁ = 66ㅁ이 될 수 없음
○ 사실 4. ㅁ6ㅁ (= 161 or 166) × ㅁ = 66ㅁ라는 점에서, ㅁ6ㅁ = 166, ㅁ = 4임을 알 수 있음
○ 사실 5. ㅁ6ㅁ (= 166) × ㅁ = ㅁ6ㅁ이라는 점에서, ㅁ = 1 또는 4임을 알 수 있음
○ 답 1. 166 × 6041 = 1,002,806 : 피제수(dividend)가 1,000,000을 초과하므로 적절히 표기하였음

○ 답 2. 166 × 6044 = 1,003,304 : 피제수(dividend)가 1,000,000을 초과하므로 적절히 표기하였음
○ 이 문제를 풀 때 다소 일반적이지 않은 사항이 있음을 유의해야 함
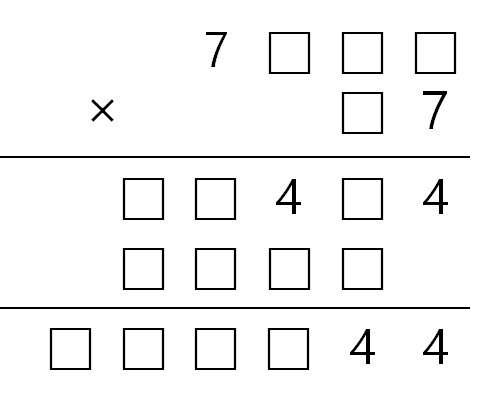
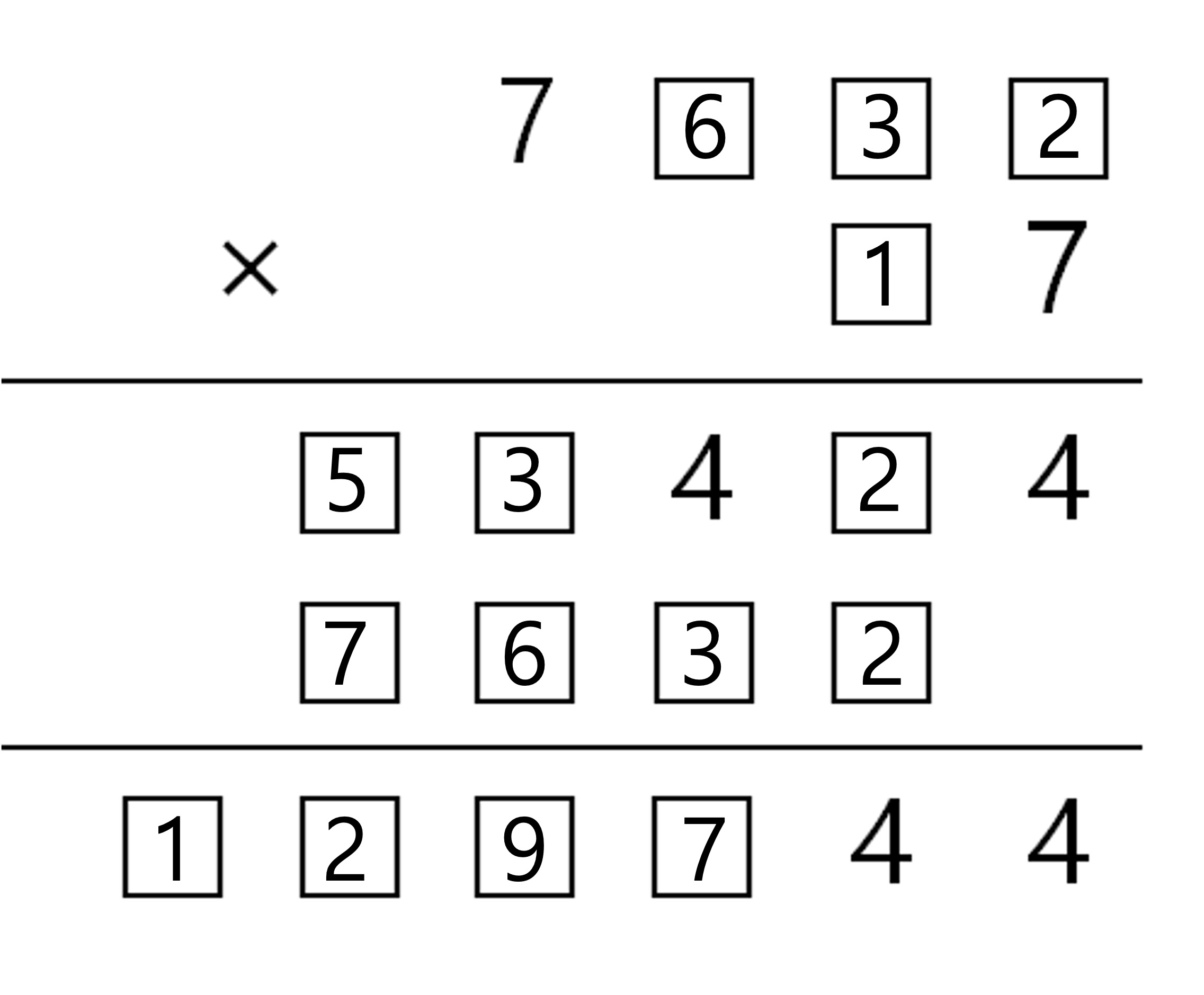
문제 2. 다음 복면산 문제에서 빈 칸을 모두 채워라.
풀이 2.
○ 먼저 알아낸 순서대로 사실을 아래와 같이 나열함
○ 사실 1. 7ㅁㅁㅁ × 7 = ㅁㅁ4ㅁ4라는 점에서, 7ㅁㅁㅁ의 일의 자리 수가 2임을 알 수 있음
○ 사실 2. 7ㅁㅁㅁ (= 7ㅁㅁ2) × ㅁ = ㅁㅁㅁㅁ라는 점에서, ㅁ = 1임을 알 수 있음
○ 사실 3. 7ㅁㅁㅁ (= 7ㅁㅁ2) × ㅁ (= 1) = ㅁㅁㅁㅁ라는 점에서, ㅁㅁㅁㅁ의 일의 자리 수가 2임을 알 수 있음
○ 사실 4. ㅁㅁ4ㅁ4 + ㅁㅁㅁㅁ0 (= ㅁㅁㅁ20) = ㅁㅁㅁㅁ44라는 점에서, ㅁㅁ424의 십의 자리 수가 2임을 알 수 있음
○ 사실 5. 7ㅁㅁㅁ (= 7ㅁㅁ2) × 7 = ㅁㅁ4ㅁ4 (= ㅁㅁ424)라는 점에서, 7ㅁㅁㅁ의 십의 자리 수가 3임을 알 수 있음
○ 사실 6. 7ㅁㅁㅁ (= 7ㅁ32) × 7 = ㅁㅁ4ㅁ4 (= ㅁㅁ424)라는 점에서, 7ㅁㅁㅁ의 백의 자리 수가 6임을 알 수 있음
○ 답 : 7632 × 17 = 129,744
○ 기본적으로 7이라는 수가 10과 서로 소에 있어 0 ~ 9과의 곱이 유니크한 1의 자리 수를 만들기 때문에 이 문제를 풀기 수월했음
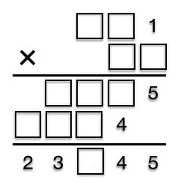
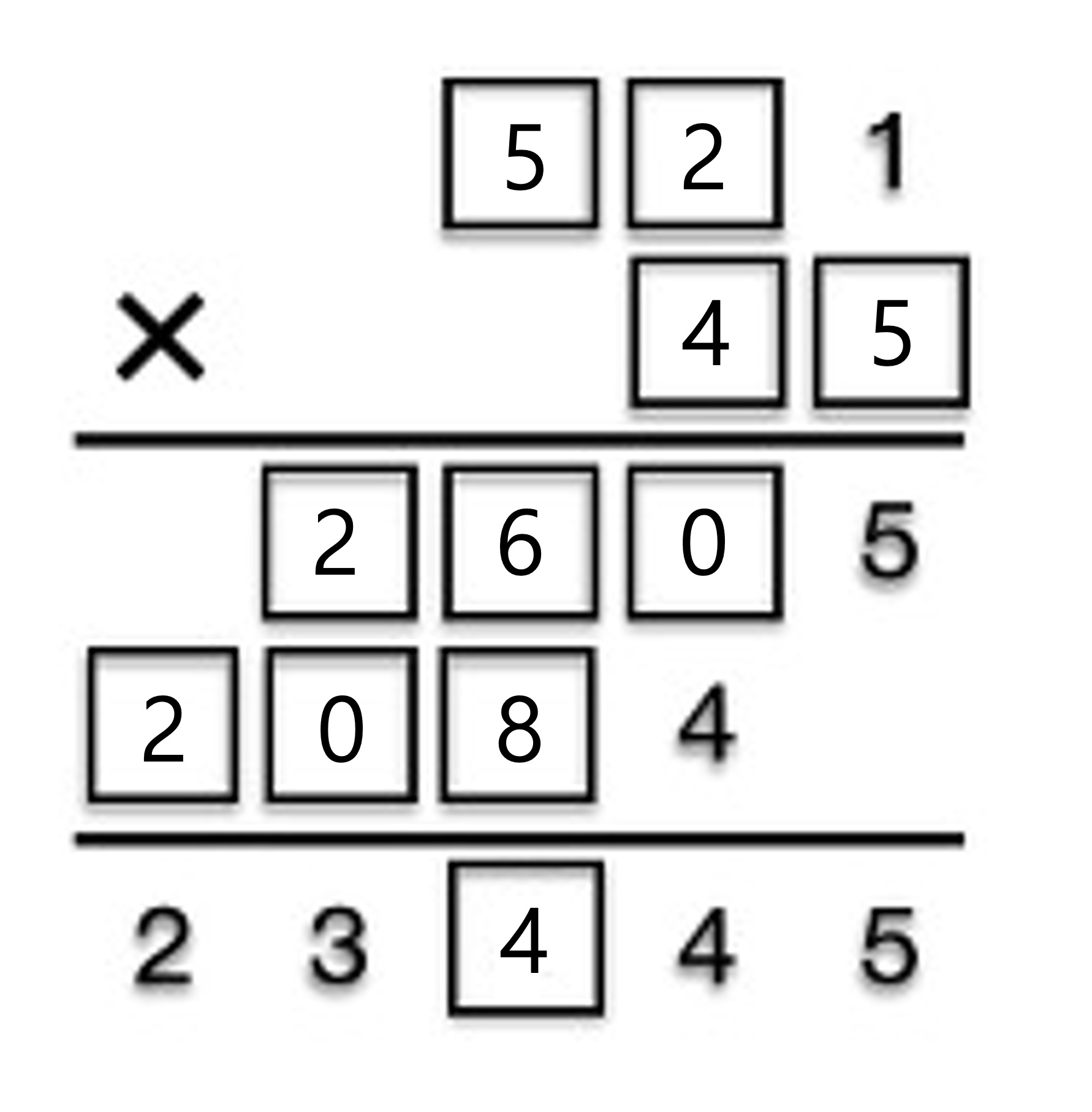
문제 3. 다음 복면산 문제에서 빈 칸을 모두 채워라.
풀이 3.
○ 먼저 알아낸 순서대로 사실을 아래와 같이 나열함
○ 사실 1. ㅁㅁ1 × ㅁ = ㅁㅁㅁ5로부터 ㅁ은 5임
○ 사실 2. ㅁㅁ1 × ㅁ = ㅁㅁㅁ4로부터 ㅁ은 4임
○ 사실 3. 23,045 ~ 23,945 중 45의 배수는 23,445밖에 없음
○ 답 : 521 × 45 = 23,445
문제 4. 10개의 숫자가 있다. 이때 1번째 숫자는 10개의 숫자 중에서 0의 개수이고, 2번째 숫자는 10개의 숫자 중에서 1의 개수이다. 이렇게 10번째 숫자는 10개의 숫자 중에서 9의 개수이다. 이때 그 10개의 숫자들을 찾아라.
풀이 4-1.
○ 먼저 알아낸 순서대로 사실을 아래와 같이 나열함
○ 사실 1. 1번째 ~ 10번째 숫자는 모두 개수를 의미하므로 다 10 이하여야 함
○ 사실 2. 만약 x번째에 10이 하나 있다면, x-1의 개수가 10개라는 의미 (단, x-1 ≤ 9) (∵ 사실 1). 그런데 10이 하나 있으므로 모순
○ 이로 인해 1번째 ~ 10번째 숫자는 다 9 이하여야 함
○ 사실 3. 만약 x번째에 9가 하나 있다면, x-1의 개수가 9개라는 의미 (단, x-1 ≤ 8). 이때 10번째에 1이 하나 있음 (∵ 9는 단 1개이므로). 따라서 x-1 = 1이므로 2번째에 9가 있고 나머지에 1이 있음 → 모순 발생 (e.g., 가령 1번째에도 1이 있어서 0이 하나라도 있어야 하는데 이는 모순)
○ 이로 인해 1번째 ~ 10번째 숫자는 다 8 이하여야 함
○ 사실 4. 만약 4 이하밖에 없다면 6번째 ~ 10번째는 모두 0이므로 0은 적어도 5개가 돼 5는 있어야 함 → 모순
○ 이로 인해 1번째 ~ 10번째 숫자 중 하나는 5 이상
○ 추론 1. 하나가 5 이상이라면 그것은 첫 번째 자리에 오는 게 타당함 : 0이 많은 것은 보통 크게 문제를 일으키지 않음
○ 추론 2. 하나가 5 이상이라면 다른 숫자들은 5 미만의 작은 숫자들로 구성돼야 함
○ 추론 3. 가장 큰 숫자가 n이고 첫 번째에 있으면, n-1번째에 1이 있어야 함. 이때, 2번째에 2가 있으며, 3번째에 1이 있는 구조밖에 안 나옴
○ 답 : (6, 2, 1, 0, 0, 0, 1, 0, 0, 0)
풀이 4-2.
○ 다음 파이썬 코드를 이용 : 풀이 4-1의 초기 시행착오를 좀 더 하면 product(range(7), repeat=10) 정도로 탐색 범위를 줄일 수 있음
from itertools import product
# 가능한 모든 숫자의 조합을 생성합니다. (0~9까지의 숫자로 구성된 10개의 조합)
possible_combinations = product(range(10), repeat=10)
# 조건을 만족하는 숫자의 조합을 찾습니다.
for combination in possible_combinations:
# 각 숫자의 개수를 저장할 리스트를 초기화합니다. (0~9까지 각 숫자의 개수)
counts = [0] * 10
# 조합에서 각 숫자의 개수를 세어 counts 리스트에 저장합니다.
for num in combination:
counts[num] += 1
# 조합이 조건을 만족하는지 확인합니다. (x번째 숫자가 x-1의 개수와 같은지)
if all(combination[i] == counts[i] for i in range(10)):
# 조건을 만족하는 조합을 출력합니다.
print(combination)
break # 첫 번째로 발견한 해답만 출력하고 반복을 종료합니다.
문제 5. 다음 조건을 만족하는 세 자리 자연수를 모두 구하여 더한 값을 구하여라.
○ 조건 1. 백의 자리는 짝수이다.
○ 조건 2. 십의 자리 숫자와 일의 자리 숫자의 차는 5이다.
○ 조건 3. 각 자리 숫자는 서로 다르고 모두 더한 합은 20 이상이다.
풀이 5-1.
○ 백의 자리 = {2, 4, 6, 8}
○ 십의 자리 + 일의 자리 = 2x - 5 (단, x = {5, 6, 7, 8, 9})
○ 백의 자리 + 십의 자리 + 일의 자리 = 2x + {-3, -1, 1, 3} ≥ 20
○ 2x ≥ {23, 21, 19, 17}
○ x ≥ {11.5, 10.5, 9.5, 8.5}이므로 x = 9
○ x = 9로부터 백의 자리 = 8이 유일하게 결정됨
○ 답은 849와 894이므로 그 합은 1743
풀이 5-2.
○ 다음과 같은 파이썬 코드를 이용 : 답은 849와 894이므로 그 합은 1743
# 조건에 맞는 세자리 자연수를 찾는 코드
# 조건:
# 1. 백의 자리는 짝수
# 2. 십의 자리 숫자와 일의 자리 숫자의 차는 5
# 3. 각 자리 숫자는 서로 다르고 모두 더한 합은 20 이상
# 가능한 세자리 자연수를 저장할 리스트
possible_numbers = []
# 가능한 백의 자리 숫자: 2, 4, 6, 8
for hundreds in [2, 4, 6, 8]:
# 가능한 십의 자리와 일의 자리 숫자 조합 탐색
for tens in range(0, 10):
for ones in range(0, 10):
# 조건 2와 3을 만족하는지 확인
if abs(tens - ones) == 5 and (hundreds + tens + ones) >= 20:
# 조건 1을 만족하는지 확인: 각 자리 숫자가 서로 다른지
if len(set([hundreds, tens, ones])) == 3:
# 모든 조건을 만족하면 리스트에 추가
possible_numbers.append(hundreds * 100 + tens * 10 + ones)
print(possible_numbers)
문제 6. 자연수를 다음과 같이 홀수개씩 묶을 때, 8은 셋째 번 묶음의 넷째 번 수이다. 300은 몇째 번 묶음의 몇째 번 수인지 구하여라.
(1), (2, 3, 4), (5, 6, 7, 8, 9), (10, 11, 12, 13, 14, 15, 16), ...
풀이 6.
○ 1 + 3 + ··· + (2k-1) = k2
○ 172 = 289 ≤ 300 ≤ 182 = 324
○ 289 + 11 = 172 + 11 = 300
○ 답 : 300은 18째 번 묶음의 11째 번 수
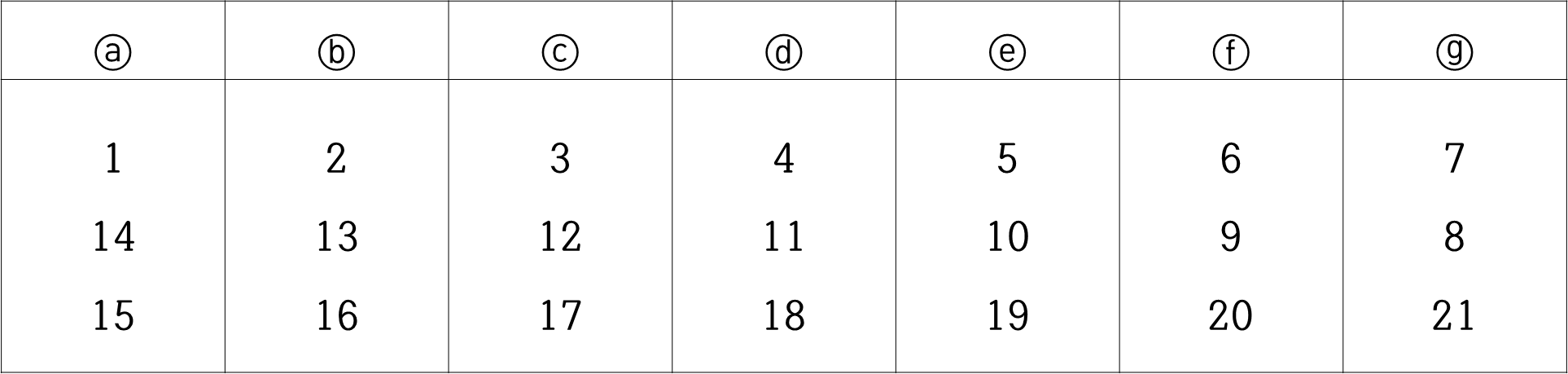
문제 7. 다음 표와 같이 자연수를 써 나갈 때, 198은 ⓐ ~ ⓖ 중 어느 글자의 줄에 쓰게 되는지 구하여라.
풀이 7.
○ 198 = 14 × 14 + 2
○ 답 : 198은 2와 같은 줄인 ⓑ에 있음
문제 8. 4장의 숫자 카드 0, 1, 2, 3이 있다. 이 중에서 2장을 뽑아서 나온 수들의 합이 점수라고 하면 나올 수 있는 점수는 모두 몇 가지인가? 그리고 이들 점수를 모두 합하면 얼마인가?
풀이 8.
○ 그림을 그려서 풀면 쉽게 풀 수 있음
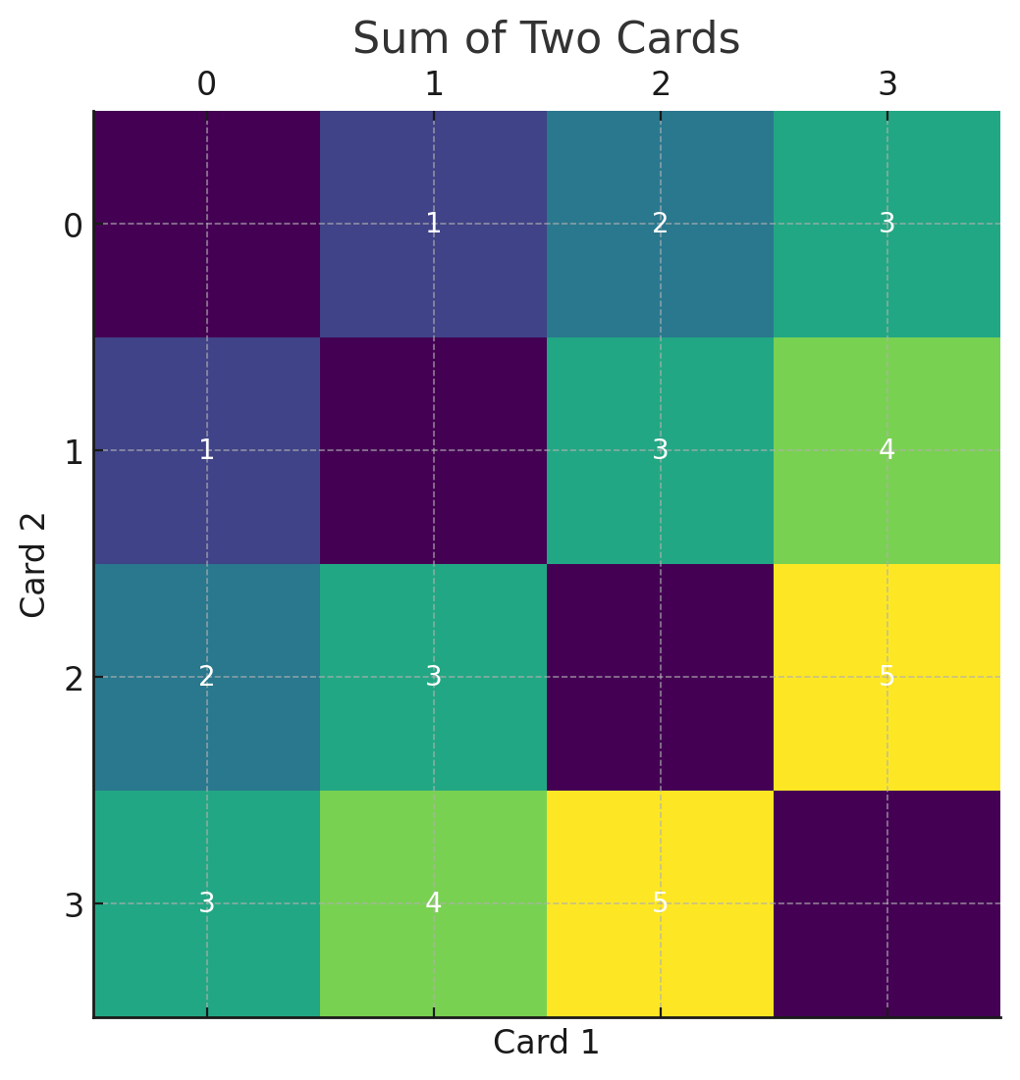
○ 답 : 1, 2, 3, 4, 5 등 5가지이며 이들의 합은 21
문제 9. 자연수를 다음과 같이 4개씩 괄호로 묶어 앞에서부터 1군, 2군, 3군, ···으로 번호를 붙여 나갈 때, 23군에 속하는 수들의 평균을 구하여라.

풀이 9.
○ n군에 포함된 수 : (4n-3, 4n-2, 4n-1, 4n)
○ 23군 : (89, 90, 91, 92)
○ 23군에 속하는 수들의 평균 : 90.5
문제 10. 아래의 수들은 일정한 규칙을 따라 배열되어 있다. 위에서 100번째 줄의 왼쪽에서 셋째 번 수는 얼마인지 구하여라.
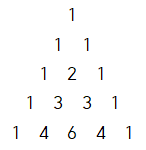
풀이 10.
○ 100번째 줄의 왼쪽에서 셋째 번 수 = 99C2 = 99 × 98 / 2 = 4851
문제 11. 세 자리 자연수 중에서 백의 자리 숫자에 3을 곱한 값이 십의 자리 숫자이고, 십의 자리 숫자보다 1 큰 값이 일의 자리 숫자인 세 자리 수를 모두 구하면 몇 개인가?
풀이 11.
○ 다음과 같은 파이썬 코드를 이용
# 세 자리 자연수 중 조건을 만족하는 숫자 찾기
def find_numbers():
count = 0
for num in range(100, 1000): # 100부터 999까지의 범위
A = num // 100 # 백의 자리 숫자
B = (num // 10) % 10 # 십의 자리 숫자
C = num % 10 # 일의 자리 숫자
# 조건 검사
if A * 3 == B and B + 1 == C:
count += 1
print(num)
return count
# 조건을 만족하는 숫자의 개수 출력
count = find_numbers()
print(f"총 {count}개의 숫자가 조건을 만족합니다.")
○ 답 : 134, 267 등 2개
문제 12. 아래의 복면산 덧셈식에서 ㄱ, ㄴ, ㄷ은 각각 서로 다른 숫자를 나타낸다. 세 자리수 ㄱㄴㄷ을 구하여라.
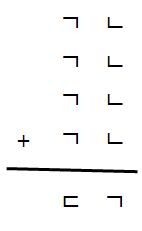
풀이 12.
○ 4 × (10 × ㄱ + ㄴ) = 40 × ㄱ + 4 × ㄴ = 10 × ㄷ + ㄱ
○ ⇔ 39 × ㄱ + 4 × ㄴ = 10 × ㄷ
○ 양변을 2로 나누면 나머지가 0이므로, ㄱ은 짝수 : ㄱ은 제일 작은 짝수인 2가 돼야 위와 같은 덧셈 구조가 될 수 있음
○ 양변을 5로 나누면 나머지가 0이므로, ㄱ + ㄴ = 5, 10, 15
○ ✅ 경우 1. 23 × 4 = 92
○ ❌ 경우 2. 28 × 4 = 112
○ 답 : 세자리 수 ㄱㄴㄷ은 239
문제 13. 어떤 네 자리 수를 순서를 거꾸로 해서 썼더니 처음의 수보다 7452 작은 네 자리 수가 되었다. 순서를 거꾸로 하기 전의 수의 첫째 숫자와 맨 끝 숫자의 합을 구하여라.
풀이 13.
○ (1000 x + 100 y + 10 z + w) - (x + 10 y + 100 z + 1000 w) = 999 x + 90 y - 90 z - 999 w = 7452
○ x - w = a ∈ {-9, ..., 9}, y - z = b ∈ {-9, ..., 9}라 두면, 999a + 90b = 7452 ⇔ 111a + 10b = 828
○ 양변을 3으로 나누면 나머지가 0이므로, b = 3p (단, p ∈ {-3, ..., 3})라 두어 37a + 10p = 276
○ 37a + 10p ≡ 2a ≡ 276 ≡ 1 (mod 5) ⇔ 6a ≡ a ≡ 3 (mod 5) ⇔ a = 5q + 3 (단, q ∈ {-2, ..., 1})
○ 이때 p ∈ {-3, ..., 3}, q ∈ {-2, ..., 1}를 brute-force하게 대입하면 p = -2, q = 1을 얻음
○ 즉, a = x - w = 8, b = y - z = -6
○ x - w = 8로부터 (x, w) = (9, 1), (8, 0)이 있을 수 있음 (e.g., 9061, 8060)
○ 그런데 8060 같은 경우 거꾸로 쓰면 0608로 되어 네 자리 수가 아님
○ 그러므로 (x, w) = (9, 1)만이 유효하므로 x + w = 10
문제 14. 다음 세 가지 조건에 알맞은 어떤 수를 구하여라.
ⓐ 어떤 수는 4보다 크고 9보다 작다.
ⓑ 어떤 수의 4배는 25보다 작다.
ⓒ 어떤 수의 5배는 25보다 크다.
풀이 14.
○ ❌ 경우 1. 어떤 수가 5인 경우 : 5배가 25보다 크지 않음
○ ✅ 경우 2. 어떤 수가 6인 경우
○ ❌ 경우 3. 어떤 수가 7인 경우 : 4배가 25보다 작지 않음
○ ❌ 경우 4. 어떤 수가 8인 경우 : 4배가 25보다 작지 않음
문제 15. 다음 7개의 숫자 사이에 +와 –를 적당히 넣어서(넣지 않아도 됨) 그 계산 결과가 55가 되도록 하여라. 또, 40이 되도록 하여라. (단, 숫자의 순서를 바꾸면 안 된다.)
1 2 3 4 5 6 7
풀이 15.
○ 다음과 같은 파이썬 코드를 이용 : 재귀함수 이용
def find_combinations(sequence, target, index=0, current_string="", current_value=0, last_value=0, results=[]):
if index == len(sequence): # 모든 숫자를 확인했을 때
if current_value == target: # 목표 값에 도달했는지 확인
results.append(current_string)
return
num = int(sequence[index])
if index == 0: # 첫 번째 숫자를 처리하는 경우
find_combinations(sequence, target, index + 1, str(num), num, num, results)
else:
# 숫자를 연결하는 경우
new_value = last_value * 10 + num if last_value >= 0 else last_value * 10 - num
find_combinations(sequence, target, index + 1,
current_string + str(num),
current_value - last_value + new_value, new_value, results)
# '+' 연산을 추가하는 경우
find_combinations(sequence, target, index + 1,
current_string + "+" + str(num),
current_value + num, num, results)
# '-' 연산을 추가하는 경우
find_combinations(sequence, target, index + 1,
current_string + "-" + str(num),
current_value - num, -num, results)
return results
# 시작점
sequence = "1234567"
results = find_combinations(sequence, 55)
print("Results:", results)
○ 55가 되는 경우 : 123+4-5-67, 12-3+45-6+7, 1+2+34+5+6+7, 1-2+3+4+56-7, 1-2-3-4+56+7
○ 40이 되는 경우 : 12+34-5+6-7, 12-34-5+67, 1-2-3+45+6-7
문제 16. 칠판에 1, 2, 3, 4, 5, …, 999, 1000을 썼다. 이때, 칠판에 적힌 숫자 1의 개수와 숫자 2의 개수의 합은 얼마인가?
풀이 16.
○ 일의 자리가 1인 경우의 수 (000 ~ 999; ㅁㅁ1) = 10 × 10 = 100개
○ 십의 자리가 1인 경우의 수 (000 ~ 999; ㅁ1ㅁ) = 10 × 10 = 100개
○ 백의 자리가 1인 경우의 수 (000 ~ 999; 1ㅁㅁ) = 10 × 10 = 100개
○ 천의 자리가 1인 경우의 수 = 1개
○ 일의 자리가 2인 경우의 수 (000 ~ 999; ㅁㅁ2) = 10 × 10 = 100개
○ 십의 자리가 2인 경우의 수 (000 ~ 999; ㅁ2ㅁ) = 10 × 10 = 100개
○ 백의 자리가 2인 경우의 수 (000 ~ 999; 2ㅁㅁ) = 10 × 10 = 100개
○ 천의 자리가 2인 경우의 수 = 0개
○ 숫자 1의 개수와 숫자 2의 개수의 합 = 301 + 300 = 601
문제 17. 다음 A, B, C, D, E, F, G는 모두 자연수일 때, 가장 큰 값을 갖게 되는 것은 어느 것인가?
A + B = C – D = E + 12 = 25 – F = G
풀이 17.
○ C = A + B + D > max (A, B, D)
○ C = D + E + 12 = G + D > max(D, E, G)
○ C = D + E + 12 ≥ 1 + 1 + 12 = 14
○ 13 = E + F ≥ 1 + F ⇔ 12 ≥ F
○ 따라서 가장 큰 값을 갖는 것은 C
문제 18. 어떤 백과사전에 적혀 있는 쪽수를 나타내는 데는 쪽수의 자리 수만큼의 활자가 필요하다. 예를 들면 135쪽에는 1, 3, 5라는 활자가 3개 필요하다. 그러면 이 백과사전의 모든 쪽수를 나타내는 데 필요한 활자의 개수가 999개라고 하면 이 백과사전은 모두 몇 쪽인지 구하여라.
풀이 18.
○ 1 ~ 9 : 9개
○ 10 ~ 99 : 2 × (99 - 10 + 1) = 180개
○ 100 ~ x : 3 × (x - 100 + 1) = 999 - (9 + 180) = 810 ⇔ x - 99 = 270 ⇔ x = 369
○ 답 : 369쪽
문제 19. 1에서 150까지의 수를 다음과 같이 차례로 쓰려고 한다. 모두 몇 개의 숫자를 써야 하는지 구하여라.
1 2 3 4 5 ··· 147 148 149 150
풀이 19.
○ 한 자리 수 : 1 ~ 9까지이므로 1 × 9 = 9개
○ 두 자리 수 : 10 ~ 99까지이므로 2 × (99 - 10 + 1) = 180개
○ 세 자리 수 : 100 ~ 150까지이므로 3 × (150 - 100 + 1) = 153개
○ 답 : 9 + 180 + 153 = 341개
문제 20. (구글 입사시험) 1 ~ 10000 사이의 8의 개수는 몇 개인가? 예를 들어, 88 ~ 90까지의 8의 개수는 88이 2개, 89가 1개, 총 3개이다.
풀이 20-1. 실제로 세 보기
○ n(___8) = n(8, 18, …, 9998) = n(0, 10, …, 9990) = n(0, 1, …, 999) = 1000
○ n(__8_) = n(80~89, 180~189, …, 9980~9989) = 10 × n(80, 180, …, 9980) = 10 × n(8, 18, …, 998) = 10 × n(0, 10, …, 990) = 10 × n(0, 1, …, 99) = 10 × 100 = 1000
○ n(_8__) = n(800~899, 1800~1899, …, 9800~9899) = 100 × n(800, 1800, …) = 100 × n(8, 18, …, 98) = 100 × n(0, 10, …, 90) = 100 × n(0, 1, …, 9) = 100 × 10 = 1000
○ n(8___) = n(8000~8999) = 1000
○ ∴ 총 개수 = 4000 개 (위에서 계속 1000이 나온다는 사실은 쉽게 일반화해서 계산할 수 있음을 보여준다.)
풀이 20-2. 확률로 풀어보기
○ 0 ~ 9999까지의 숫자를 고려해 보자. 그 숫자들 중 1의 자리가 8인 숫자를 뽑을 확률은 정확히 1/10임을 알 수 있다. (by 대칭성)
○ 그런데 10의 자리가 8인 숫자를 뽑을 확률도 1/10이 아닐 이유가 없다. (오히려 1/10이 아니면 이상하다.)
○ 이는 100의 자리, 1000의 자리도 마찬가지다.
○ 따라서 1의 자리에 있는 8의 개수는 다른 자리에 있는 8의 개수와 같으며 그 수는 정확히 10000 × 0.1 = 1000개 이다. 즉, 8의 전체 개수는 1, 10, 100, 1000의 자리의 8의 개수를 모두 더해준 4000이다.
입력: 2022.05.20 10:43
수정: 2024.02.24 02:05
'▶ 자연과학 > ▷ 정수론' 카테고리의 다른 글
| 【정수론】 정수 집합과 필요충분조건 (0) | 2022.08.21 |
|---|---|
| 【정수론】 정수론 노트 (0) | 2020.12.14 |
| 【정수론】 대수경 중 수열·급수 문제 모음 (0) | 2016.06.25 |
| 【정수론】 페르마에 대해 간단한 조사 (0) | 2016.06.21 |
| 【정수론】 정수론 목차 (0) | 2016.06.21 |


최근댓글