The Solution for GRE Mathematics Practice Test [41-60]
추천글 : 【GRE】 Solution for GRE Mathematics Practice Test
41. Let ℓ be the line that is the intersection of the planes x + y + z = 3 and x - y + z = 5 in ℝ3. An equation of the plane that contains (0, 0, 0) and is perpendicular to ℓ is

⑴ answer: A
⑵ ℓ = {(x, y, z) | y = -1, x + z = 4}
⑶ The direction vector of ℓ = (1, 0, -1) = The normal vector of the resultant plane
42. Let ℤ+ be the set of positive integers and let d be the metric on ℤ+ defined by

for all m, n ∈ ℤ+. Which of the following statements are true about the metric space (ℤ+, d)?


⑴ answer: E
⑵ solution
How does the metric space impact the property of subset?
The question is: let $\mathbb{Z}^+$ be the set of positive integers and let d be the metric on $\mathbb{Z}^+$ defined by $d(m, n) = \begin{cases} 0\text{ if }m = n\\ 1 \text{ if } m \neq n \end{cas...
math.stackexchange.com
43. A curve in the xy-plane is given parametrically by
x = t2 + 2t
y = 3t4 + 4t3
for all t > 0. The value of d2y/dx2 at the point (8, 80) is
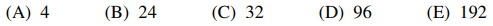
⑴ answer: A
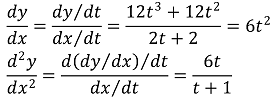
44. If y is a real-valued function defined on the real line and satisfying the initial value problem below,
y' + xy = x
y(0) = -1
then
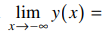
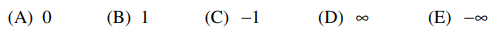
⑴ answer: B
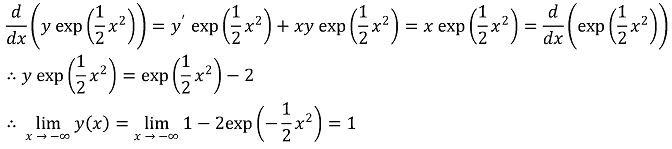
45. How many positive numbers x satisfy the equation cos (97x) = x?
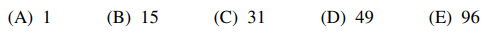
⑴ answer: C
⑵ 97 / (2π) = 15.43803
⑶ For every period, there are two intersections between y = cos (97x) and y = x.
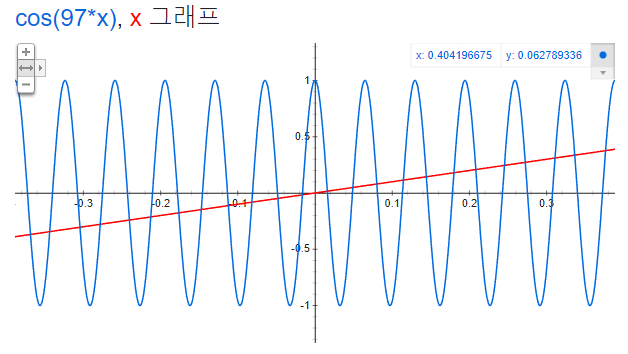
⑷ For the last 0.43803 turn, only downward trend of the function y = cos (97x) exists, making only one solution.
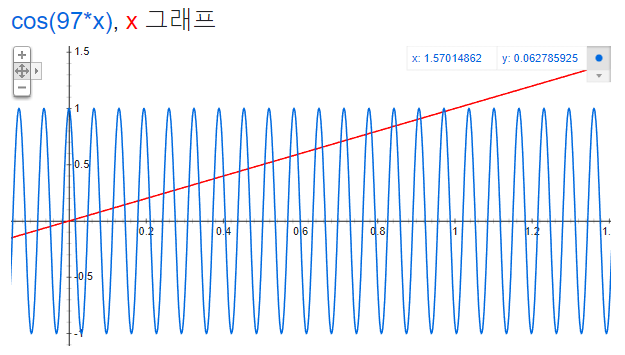
⑸ ∴ 15 × 2 + 1 = 31
46. A ladder 9 meters in length is leaning against a vertical wall on level ground. As the bottom end of the ladder is moved away from the wall at a constant rate of 2 meters per second, the top end slides downward along the wall. How fast, in meters per second, will the top end of the ladder be sliding downward at the moment the top end is 3 meters above the ground?
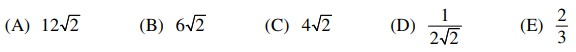
⑴ answer: C
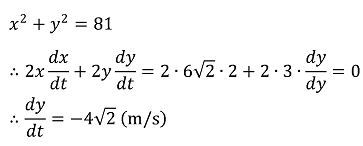
47. The function f : ℝ → ℝ is defined as follows.
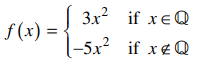
Which of the following is true?
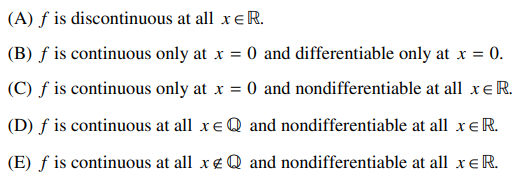
⑴ answer: B
⑵ continuity ⇔ 3x2 = -5x2 ⇔ x = 0
⑶ differentiability
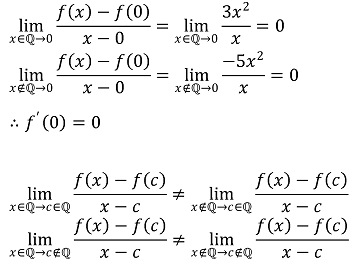
48. Let g be the function defined by g(x, y, z) = 3x2y + z for all real x, y, and z. Which of the following is the best approximation of the directional derivative of g at the point (0, 0, π) in the direction of the vector i + 2j + 3k? (Note: i, j, and k are the standard basis vectors in ℝ3.)
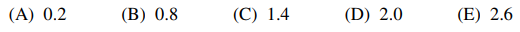
⑴ answer: B
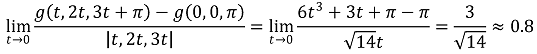
49. What is the largest order of an element in the group of permutations of 5 objects?
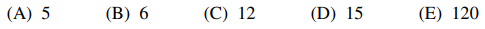
⑴ answer: B
⑵ solution
Element of Largest Order in $S_n$
What is the largest order of an element in the group of permutations of $5$ objects? Let $\sigma \in S_5$ be arbitrary. We know that $\sigma = \sigma_1...\sigma_k$, where the $\sigma_i$'s are disj...
math.stackexchange.com
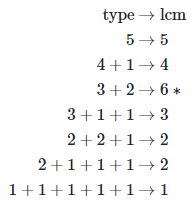
50. Let R be a ring and let U and V be (two-sided) ideals of R. Which of the following must also be ideals of R?
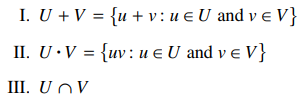
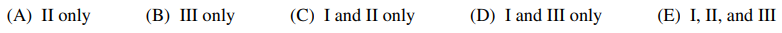
⑴ answer: D
⑵ solution
Problem 50 in GRE Practice book: Ideals of a ring
The GRE Practice book includes this problem (#50). Let $R$ be a ring and let $U$ and $V$ be (two-sided) ideals of $R$. Which of the following must also be ideals of $R$ ? I. $U + V = \{ u + v : u ...
math.stackexchange.com
51. Which of the following is an orthonormal basis for the column space of the real matrix
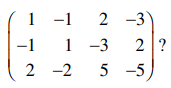
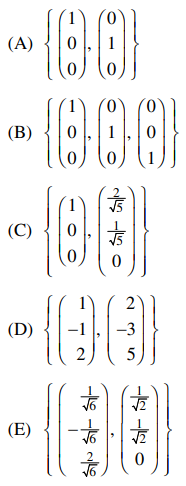
⑴ answer: E
⑵ Gram-Schmidt orthogonalization process
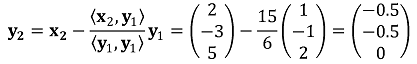
52. A university’s mathematics department has 10 professors and will offer 20 different courses next semester. Each professor will be assigned to teach exactly 2 of the courses, and each course will have exactly one professor assigned to teach it. If any professor can be assigned to teach any course, how many different complete assignments of the 10 professors to the 20 courses are possible?
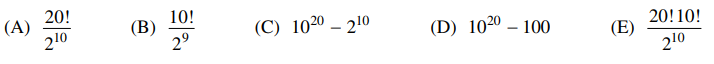
⑴ answer: A
⑵ Calculate 20 classes in permutation, and then organize unnecessary double duplication for each professor.
53. Let f and g be continuous functions of a real variable such that
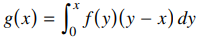
for all x. If g is three times continuously differentiable, what is the greatest integer n for which f must be n times continuously differentiable?
⑴ answer: A
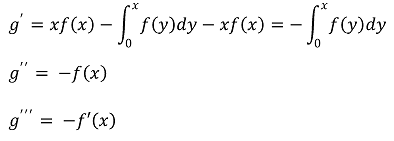
54. If a real number x is chosen at random in the interval [0, 3] and a real number y is chosen at random in the interval [0, 4], what is the probability that x < y?
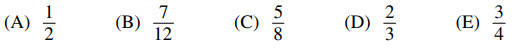
⑴ answer: C
⑵ p = The area of interest / Total area = [ (1 + 4) / 2 × 3 ] / [ 4 × 3 ] = 5 / 8
55. If a and b are positive numbers, what is the value of
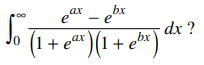
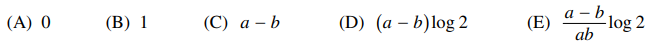
⑴ answer: E
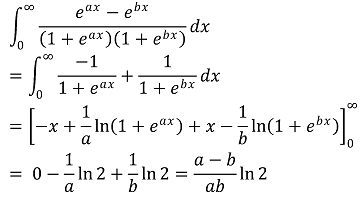
56. Which of the following statements are true?
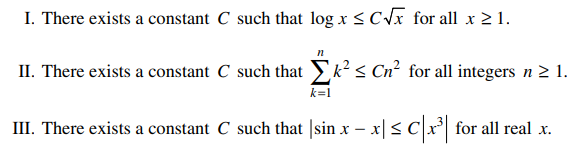
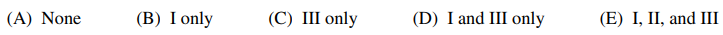
⑴ answer: D
⑵ Ⅰ. (ln x)' = 1 / x ≤ (√x)' = 1 / (2√x) for x ≥ 4.
⑶ Ⅱ. There exists m that satisfies mx3 ≤ ∑ k2. It could be assured by the geometric meaning of integration.
⑷ Ⅲ. It could be verified by a graph.
57. For each positive integer n, let xn be a real number in the open interval (0, 1/n). Which of the following statements must be true?

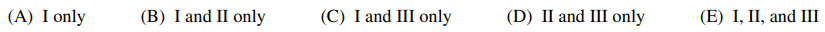
⑴ answer: C
⑵ Ⅰ. When (0, 1/n) becomes (0, 0), xn must converge to 0.
⑶ Ⅱ. f(x) = 1 / x diverges.
⑷ Ⅲ. lim g(xn) = g(0).
58. A circular helix in xyz-space has the following parametric equations, where θ ∈ ℝ.
x(θ) = 5 cos θ
y(θ) = 5 sin θ
z(θ) = θ
Let L(θ) be the arc length of the helix from the point P(θ) = (x(θ), y(θ), z(θ)) to the point (5, 0, 0), and let D(θ) be the distance between P(θ) and the origin. If L(θ0) = 26, then D(θ0) =
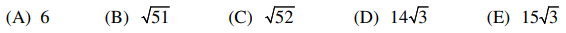
⑴ answer: B
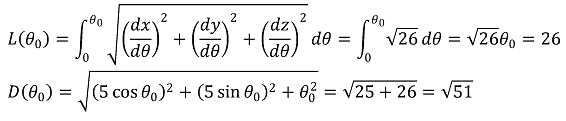
59. Let A be a real 3 × 3 matrix. Which of the following conditions does NOT imply that A is invertible?

⑴ answer: E
⑵ 🄓 It means the rank of A is 3, thus A is invertible.
⑶ 🄔 There may be three vectors with nonzero image, but they may all be sent to the same vector so it doesn't guarantee that the image has dimension 3.
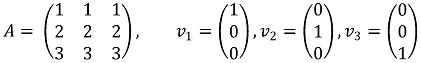
60. A real-valued function f defined on ℝ has the following property.
For every positive number ϵ, there exists a positive number δ such that
| f(x) - f(1) | ≥ ϵ whenever | x - 1 | ≥ δ
This property is equivalent to which of the following statements about f?

⑴ answer: D
⑵ It is obvious.
입력: 2023.01.21 18:02
'▶ 자연과학' 카테고리의 다른 글
| 【GR1724】 The Solution for GRE Biology Practice Test [01-20] (4) | 2023.05.06 |
|---|---|
| 【GR1768】 The Solution for GRE Mathematics Practice Test [61-66] (0) | 2023.01.22 |
| 【GR1768】 The Solution for GRE Mathematics Practice Test [21-40] (0) | 2023.01.21 |
| 【GR1768】 The Solution for GRE Mathematics Practice Test [01-20] (0) | 2023.01.14 |
| 【GR1776】 The Solution for GRE Physics Practice Test [81-100] (0) | 2023.01.01 |

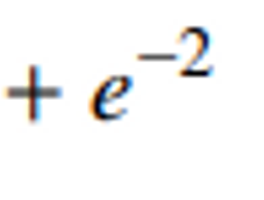
최근댓글