The Solution for GRE Mathematics Practice Test [21-40]
추천글 : 【GRE】 Solution for GRE Mathematics Practice Test
21. What is the value of


⑴ answer: B
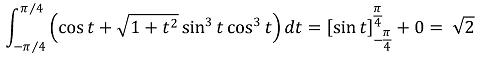
22. What is the volume of the solid in xyz-space bounded by the surfaces y = x2, y = 2 - x2, z = 0, and z = y + 3?
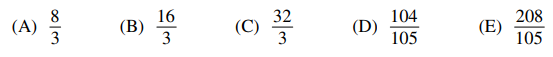
⑴ answer: C

23. Let (ℤ10, +, ·) be the ring of integers modulo 10, and let S be the subset of ℤ10 represented by {0, 2, 4, 6, 8}. Which of the following statements is FALSE?

⑴ answer: D
⑵ 🄐 0 + 2 = 2 ∈ S, 4 + 6 = 10 ≡ 0 ∈ S, 6 + 8 = 14 ≡ 4 ∈ S, ···
⑶ 🄑 0 × 2 = 0 ∈ S, 4 × 6 = 24 ≡ 4 ∈ S, 6 × 8 = 48 ≡ 8 ∈ S, ···
⑷ 🄒 0 is the identity under addition modulo 10. For example, 8 + 0 (identity) = 8 (mod 10).
⑸ 🄓 6 is the identity under multiplication modulo 10. For example, 8 × 6 (identity) = 48 ≡ 8 (mod 10).
⑹ 🄔 It's obvious.
24. Consider the system of linear equations
w + 3x + 2y + 2z = 0
w + 4x + y + 0z = 0
3w + 5x + 10y + 14z = 0
2w + 5x + 5y + 6z = 0
with solutions of the form (w, x, y, z), where w, x, y, and z are equal. Which of the following statements is FALSE?

⑴ answer: E
⑵ 🄑, 🄓 (-5, 1, 1, 0) is a solution and the determinant of the linear mapping is 0.
⑶ 🄒 by linearity
⑷ 🄔 when solved, x = 2n+w, y = -8n-5w, z = 5n + 3w
25. The graph of the derivative h' is shown below, where h is a real-valued function. Which of the following open intervals contains a value c for which the point (c, h(c)) is an inflection point of h?
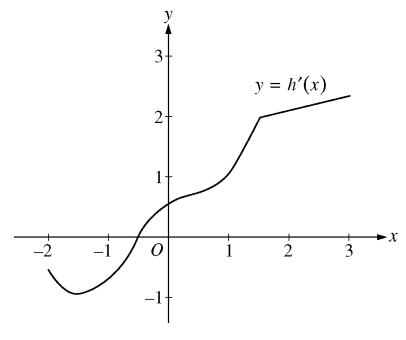
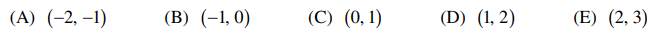
⑴ answer: A
⑵ inflection point : h''(x) = 0, thus h'(x) should have one or more extremal values in the given interval.
26. If x and y are integers that satisfy the congruences below, then x + y is congruent modulo 11 to which of the following?
3x ≡ 5 (mod 11)
2y ≡ 7 (mod 11)
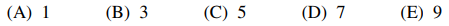
⑴ answer: D
⑵ 12x ≡ x ≡ 20 ≡ 9 (mod 11)
⑶ 12y ≡ y ≡ 42 ≡ 9 (mod 11)
⑷ ∴ x + y ≡ 18 ≡ 7 (mod 11)
27. Answer the following
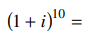
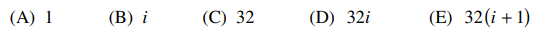
⑴ answer: D
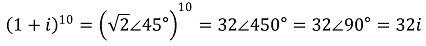
28. Let f be a one-to-one (injective), positive-valued function defined on ℝ. Assume that f is differentiable at x = 1 and that in the xy-plane the line y - 4 = 3(x - 1) is tangent to the graph of f at x = 1. Let g be the function defined by g(x) = √ x for x ≥ 0. Which of the following is FALSE?
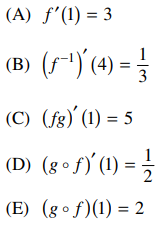
⑴ answer: D
29. A tree is a connected graph with no cycles. How many nonisomorphic trees with 5 vertices exist?
⑴ answer: C

30. For what positive value of c does the equation log x = cx4 have exactly one real solution for x?
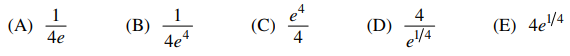
⑴ answer: A
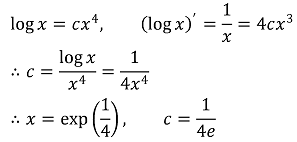
31. Of the numbers 2, 3, and 5, which are eigenvalues of the matrix
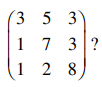
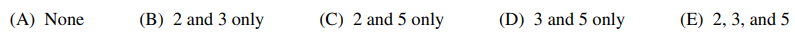
⑴ answer: C
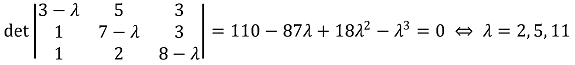
32. Answer the following
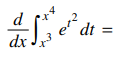
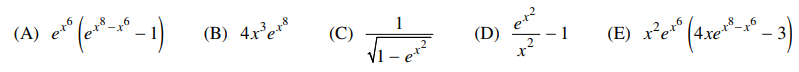
⑴ answer: E
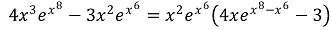
33. What is the 19th derivative of
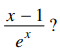
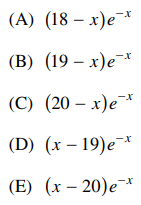
⑴ answer: C
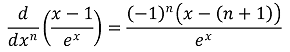
34. Which of the following statements about the real matrix shown below is FALSE?
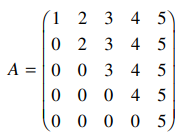

⑴ answer: B
⑵ If Ax = x, x = (c, 0, 0, 0, 0) for c ∈ ℝ.
35. In xyz-space, what are the coordinates of the point on the plane 2x + y + 3z = 3 that is closest to the origin?
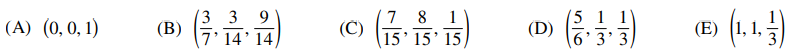
⑴ answer: B
⑵ (2t, t, 3t) ∈ {(x, y, z) | 2x + y + 3z = 3} ⇔ (3/7, 3/14, 9/14)
36. Suppose S is a nonempty subset of ℝ. Which of the following is necessarily true?

⑴ answer: C
⑵ {v ∈ S} is made up of all open sets overlapping within S and is inevitably an open set.
37. Let V be a finite-dimensional real vector space and let P be a linear transformation of V such that P2 = P. Which of the following must be true?

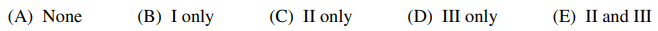
⑴ answer: C
⑵ Ⅰ. P can be the zero transformation.
⑶ Ⅱ. Suppose A is n × n, and let v an eigenvector of A with eigenvalue λ. Using A2 = A, it is easy to check that (A - λI)2 = ±(A - λI) when λ = 0, 1. Thus, any (nonzero) generalized eigenvector of A is also an eigenvector of A. Since the generalized eigenvectors of an n × n matrix always span ℝn, we conclude that the eigenvectors of A span ℝn, so A is diagonalizable.
⑷ Ⅲ. There is an example that is not the identity transformation nor the zero transformation.
38. The maximum number of acute angles in a convex 10-gon in the Euclidean plane is
⑴ answer: C
⑵ The convex 10-gon can exist with 3 acute angles and cannot be convex when there are 4 90 degrees in a given shape, so there are up to 3 acute angles.
39. Consider the following algorithm, which takes an input integer n > 2 and prints one or more integers.

If the input integer is 88, what integers will be printed?

⑴ answer: D
40. Let S be the set of all functions f : ℝ → ℝ. Consider the two binary operations + and ∘ on S defined as pointwise addition and composition of functions, as follows.
(f + g)(x) = f(x) + g(x)
(f ∘ g)(x) = f(g(x))
Which of the following statements are true?

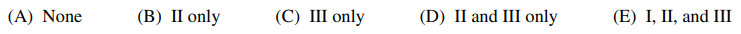
⑴ answer: C
⑵ Ⅰ. If f(x) = x + 1 and g(x) = x2, (f ∘ g)(x) = x2 + 1 and (g ∘ f)(x) = (x + 1)2. So ∘ is not commutative.
⑶ Ⅱ. If f(x) = x2, g(x) = 2x + 1, and h(x) = x + 3, f ∘ (g + h) = (3x + 4)2 and (f ∘ g) + (f ∘ h) = (2x + 1)2 + (x + 3)2.
입력: 2023.01.21 12:44
'▶ 자연과학' 카테고리의 다른 글
| 【GR1768】 The Solution for GRE Mathematics Practice Test [61-66] (0) | 2023.01.22 |
|---|---|
| 【GR1768】 The Solution for GRE Mathematics Practice Test [41-60] (0) | 2023.01.21 |
| 【GR1768】 The Solution for GRE Mathematics Practice Test [01-20] (0) | 2023.01.14 |
| 【GR1776】 The Solution for GRE Physics Practice Test [81-100] (0) | 2023.01.01 |
| 【GR1776】 The Solution for GRE Physics Practice Test [61-80] (0) | 2022.12.30 |
최근댓글