7-1강. 고지자극의 위경도 계산
추천글 : 【지구과학】 7강. 지구의 역장
현재 지구를 기준으로 트라이아스기 때의 고지자극의 위경도를 구해보자.

그림 1
우선 당시의 고지자극이 현재 자극과 위도상 같은 방향에 있다고 하자. 그러면 주어진 문제를 위와 같이 나타낼 수 있다(위 도식은 지구중심 쌍극자설에 근거하여 진북극과 자북극을 동일하다고 보았다). 이는 지구를 앞에서 바라본 그림(좌)과 지구를 위에서 바라본 그림(우)을 따로 나타내었다. 각각의 그림에 주어진 조건을 표시하였으며 색칠된 원은 트라이아스기 당시의 고지자극의 위치를 나타낸다.
먼저 좌측의 그림을 통해 트라이아스기 당시 고지자극의 위도를 알아낼 수 있다. 우선 λ는 암석 형성 당시의 위도로서 이 값을 구하면 아래와 같다.
tan I = 2 tan λ (I = + 35를 대입)
tan 35° × (1/2) = 0.70021 × (1/2) = 0.35011 = tan λ
⇔ λ = tan-10.35011 = 19.296°
그러므로 고지자극의 위도는 다음과 같다.
180 - (90 + (37 - λ)) = 180 - (127 - 19.296) = 180 - 107.704 = 72.296°N
한편 우측의 그림을 통해 트라이아스기 당시 고지자극의 경도를 알 수 있다. 오른쪽 그림에서 A는 앞서 구한 고지자극의 위도를 참고하면 A = cos 72.296° = 0.3041임을 알 수 있다. 오른쪽 그림은 위에서 투영한 이미지임을 상기하자. 이를 제이코사인 법칙을 적용하면 다음과 같은 결론에 도달한다(단, 오른쪽 그림은 원주 위에 암석 산출 장소가 놓이므로 반지름이 0.79864이다).
A2 = cos2 37° + B2 - 2B cos 37° × cos 70°
⇔ D/4 = -0.47073 < 0 (B에 대한 이차방정식에서)
이는 B의 값이 결정되지 않음을 의미하고 그 원인은 앞서 내렸던 전제를 통해 살펴볼 수 있다. 즉, 당시의 지자극은 현재 자극과 위도상 반대 방향에 있었던 것이다. 그러면 주어진 문제는 아래와 같이 나타낼 수 있다.
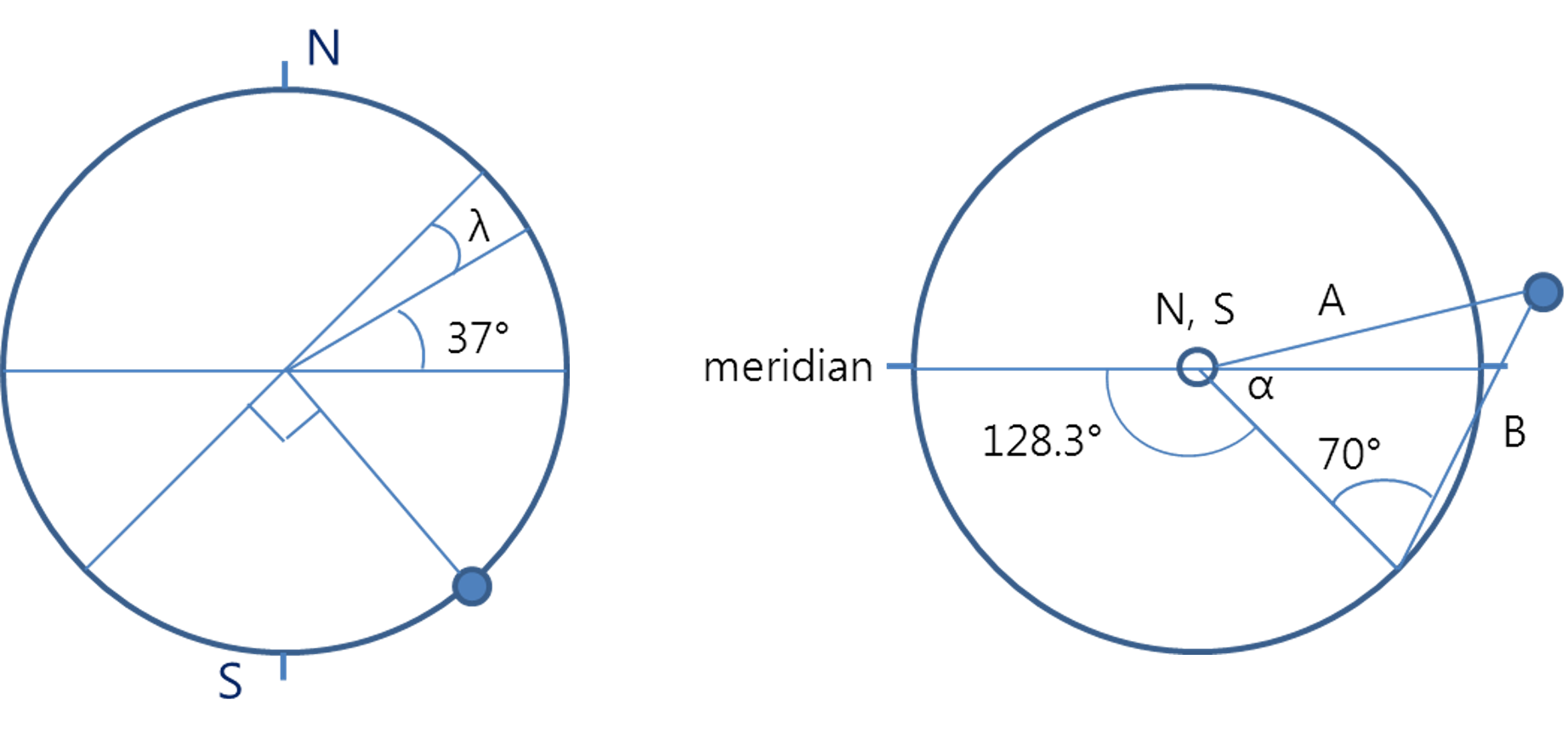
그림 2
위의 그림에서 나타난 λ는 앞서 구했듯 19.296°이다. 그렇다면 고지자극의 위도는 90°에서 37°과 19.296°를 뺀 값만큼 남쪽, 그러니까 33.704°S이다. 따라서 오른쪽 그림에서와 같이 산출 장소를 반지름으로 잡은 원에서 지자극의 위치가 밖으로 벗어난다.
한편, A = cos 33.704° = 0.83192임은 앞서 구한 방법과 같다. 이를 제이코사인 법칙을 적용하면 아래와 같은 전개가 가능하다.
B2 + cos237° - 2Bcos37° × cos70° = A2
⇔ 2B = 2cos37° × cos70° ± 2√[cos237 cos270 - (cos237 - A2)]
⇔ B = 0.273149431 ± 0.359002535
⇔ B = 0.63151966 또는 -0.085853104에서 B > 0이므로 B = 0.632151966
이제 사인법칙을 적용하면 아래와 같은 전개가 가능하다.
sin α / B = sin 70° / A = sin 70° / 0.83192
⇔ α = sin-1(0.632151966 × sin 70° ÷ 0.83192)
⇔ α ≃ 45.6 °
이를 통해 고지자극의 경도는 173.9°임을 알 수 있다. 정리하면 고지자극의 위경도를 현재 지구상에 표시하면 위도 72.296°N, 경도 173.9°E이다. 단, 이 모든 풀이는 암석이 형성된 이후로 위치가 변하지 않았다는 가정을 내포한다.
입력: 2022.11.20 10:50
'▶ 자연과학 > ▷ 지구과학' 카테고리의 다른 글
| 【지구과학】 2-1강. 월식의 주기 (0) | 2016.06.27 |
|---|---|
| 【물리학】 현대물리학 3강. 현대우주론 (0) | 2016.06.26 |
| 【지구과학】 4강. 우주 (0) | 2016.06.22 |
| 【지구과학】 3강. 항성(별) (0) | 2016.06.22 |
| 【지구과학】 2강. 태양계 (0) | 2016.06.22 |




최근댓글