2-1강. 월식의 주기(ref)
추천글 : 【지구과학】 2강. 태양계
Q. 지구에서 2015년 월식이 일어나는 주기를 계산한 식을 인터넷에서 찾아보고, 이 식이 어떻게 유도되었는지를 역학적·천문학적으로 설명하라.
A.
지구를 기준으로 공전하는 달의 공전주기는 약 27.212일이 걸린다. 이때 달은 근사적으로 지구를 중심으로 하는 하나의 원을 그린다. 따라서 지구를 중심으로 하는 천구에 대해서 달은 약 27.212일의 주기를 가지고 지구를 중심으로 하는 대원(즉, 백도)을 그리며 운동한다.
또한 해가 교점을 지난 뒤 다시 그 교점에 돌아오는 데는 약 346.6일이 걸린다. 따라서 지구를 중심으로 하는 천구에 대해서 태양은 약 346.6일의 주기를 가지고 지구를 중심으로 하는 대원(즉, 황도)을 그리며 운동한다.
이때 월식이 일어나기 위한 조건을 구해보자.
Figure. 1. 월식의 주기를 계산하기 위한 모델
지구와 태양의 공통접선의 접점에서 지구와의 거리는,

Figure. 2. 월식의 주기를 계산하기 위한 모델
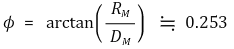
따라서 월식이 일어나기 위해서는 태양-지구를 잇는 연장선에 대해서 달-지구를 잇는 직선이 0.692° + 0.253° = 0.945° 이하의 각도를 이뤄야 한다. 그 중에서 개기월식이 일어나기 위해서는 태양-지구를 잇는 연장선에 대해서 달-지구를 잇는 직선이 0.692° - 0.253° = 0.439° 이하의 각도를 이뤄야 한다. (기본적으로 월식은 태양에 의한 지구의 그림자가 달을 가리는 현상이기 때문에 태양 반대쪽 부근에 달이 있어야 함은 자명하다.)
2015년 4월 4일에 개기월식이 일어났다. 따라서 논의를 간단히 하기 위해 2015년 4월 4일에 태양과 지구를 잇는 직선상에 달이 놓였다고 가정하자. 그런데 황도는 천구의 중심을 지나는 대원이기 때문에 태양의 반대편도 황도에 놓인다. 따라서 위의 가정에 의해 달은 황도와 백도의 교점에 위치한다. 따라서 태양도 황도와 백도의 교점에 위치한다.
이때 다음 월식의 주기를 생각해 보자. 천구를 단위구로 생각해 보았을 때 천구상의 태양의 좌표를 (cosωSt, sinωSt cosρ, sinωSt sinρ), 달의 좌표를 (-cosωMt, -sinωMt, 0)으로 둘 수 있어서, 원점(지구)에 대한 태양의 반대쪽 점 (-cosωSt, -sinωSt cosρ, -sinωSt sinρ)에 해당하는 벡터와 달의 좌표에 해당하는 벡터의 내적의 관계식으로 표현할 수도 있다. 그것은 제언으로 남겨 두고자 한다.
보다 간단하게 주기를 구하기 위해서 최소공배수의 아이디어를 이용한다. 월식이 일어나기 위한 조건을 보았을 때, 태양, 지구, 달이 거의 일직선에 존재했어야 했다. 그리고 이는 황도와 백도의 교점에 서로 반대편으로 태양과 달이 존재해야 함을 말한다. 따라서 어떤 시간 T가 지났을 때 다시 월식이 일어난다는 것은, 태양은 황도를 반정수 배만큼 회전했고 달도 백도를 반정수 배만큼 회전했다는 것과 필요충분이다. 단, 태양과 달은 반대편에 위치해야 한다.
그 논리에 따라서 조사해 보았을 때, 346.6 × 19 = 6585.4 (일), 27.212 × 242 = 6585.3 (일)이 되어 비교적 근사하게 월식의 주기를 만족한다. ('근사'하다는 것은 사실 제언에서 밝혀둔 것처럼 증명할 수 있을 것이다.)
그리고 이를 사로스 주기라고 한다.
입력: 2015.09.18 20:08
'▶ 자연과학 > ▷ 지구과학' 카테고리의 다른 글
| 【지구과학】 6강. 지구의 운동 (0) | 2019.03.23 |
|---|---|
| 【지구과학】 5강. 지구의 구조 (0) | 2019.03.22 |
| 【물리학】 현대물리학 3강. 현대우주론 (0) | 2016.06.26 |
| 【지구과학】 7-1강. 고지자극의 위경도 계산 (0) | 2016.06.23 |
| 【지구과학】 4강. 우주 (0) | 2016.06.22 |






최근댓글