3항 점화식
추천글 : 【수학】 수학 목차
Q.
다음 조건을 만족하는 수열 {an}n≥1의 일반항은?

Solution.
p = 0인 경우 식은 다음과 같다.
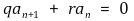
이때 q = 0이든, q ≠ 0이든 an은 등비수열이다.
그 경우 일반항은 매우 쉽게 구할 수 있으므로 p ≠ 0이라고 가정하자.
비슷하게 q = 0 또는 r = 0인 경우도 제외하자.

경우 1. 다음 식이 서로 다른 두 근 α, β를 갖는 경우

점화식도 비슷한 형태로 고칠 수 있다.

이때 n = -1인 경우 (우변) = a1이 성립한다.
비슷하게, n = 0인 경우 (우변) = a2가 성립한다.
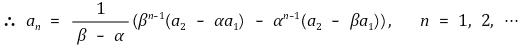
따라서 점화식을 풀 때 다음과 같은 꼴로 둘 수 있다.
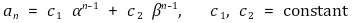
경우 2. 다음 식이 중근 α ≠ 0을 갖는 경우
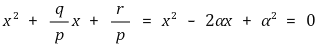
점화식도 비슷한 형태로 고칠 수 있다.
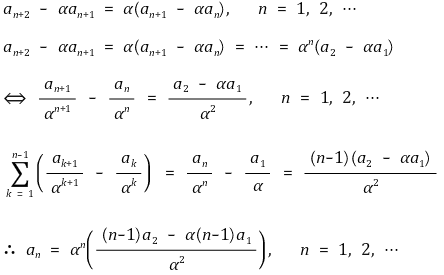
따라서 점화식을 풀 때 다음과 같은 꼴로 둘 수 있다.
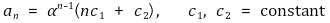
입력: 2015.10.31
'▶ 자연과학 > ▷ 대수학' 카테고리의 다른 글
| 【선형대수학】 1강. 벡터공간 (0) | 2020.04.06 |
|---|---|
| 【선형대수학】 선형대수학 목차 (0) | 2017.08.06 |
| 【선형대수학】 대수경 중 선형대수학 문제 모음 (9) | 2016.06.25 |
| 【선형대수학】 6강. 선형대수학과 머신러닝 (0) | 2016.06.25 |
| 【선형대수학】 프로베니우스 rank 부등식 (Frobenius' Inequality) (1) | 2016.06.24 |




최근댓글