4강. 비정상상태의 열전도
추천글 : 【열전달】 열전달 목차
1. 비정상상태의 열전도 [본문]
2. 집중 열용량계 [본문]
3. 지배방정식 [본문]
4. Hisler chart [본문]
5. 수치해석적 방법 [본문]
1. 비정상상태의 열전도(unsteady-state heat conduction) [목차]
⑴ unsteady-state : 정상상태 전의 상태(transient state before steady-state)
2. 집중 열용량계(lumped heat capacity system) [목차]
⑴ 계의 분류
① 분포정수(변량)계 (Distributed parameter system)
○ 위치에 따라 물리량이 다르게 전달되는 것
○ 편미분 방정식(PDE)이 사용됨
② 집중정수(변량)계 (Lumped parameter system)
○ 물체의 내부저항이 외부저항에 비해 무시할 수 있다고 가정하는 방법으로 물체 내부 위치에 따른 물리량의 편차를 무시함
○ 집중 열용량계의 경우 위치에 따라 온도가 일정하다고 가정한다.
○ 상미분 방정식(ODE)이 사용됨
③ Biot number

단, Lc는 대표길이로 대개 다음과 같은 값을 취하고 있다.
(무난하게 쓰일 수 있는 값일 뿐, 엄밀한 의미가 있는 건 아니다.)

평면, 실린더, 구에서의 대표길이는 아래와 같다.
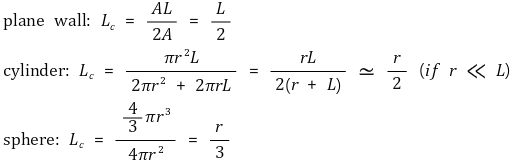
④ Biot number가 0.1 보다 작으면 집중정수계로 가정할 수 있다.
○ Bi ≪ 0.1 : 물체 내부의 온도차 < 대류면에서의 온도차 ⇒ 물체를 한 점으로 취급
○ Bi > 0.1 : 온도가 일정한 한 덩어리로 가정할 수 없다.
⑵ 예제 1

Figure. 1. 예제 1
공의 내부 에너지 변화량이 대류로 나간 열과 같다는 방정식을 세울 수 있다.
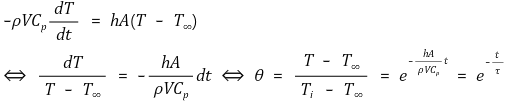
이때 τ를 열 시간상수 (thermal time constant)라고 한다.
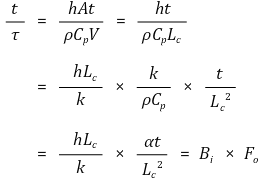
위에서 Fo를 푸리에 수(Fourier number)라고 한다.

3. 지배방정식(governing equation) [목차]
⑴ 수학적 표현
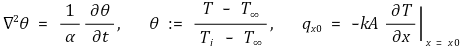
⑵ 문제 1. 두께 2L을 가지는 무한 평면
① θ (x, t) = X(x) × Y(t)의 선형합으로 나타난다고 가정
○ 모든 물리식은 연속이고 미분가능 → 항상 푸리에 급수로 표현 가능
○ 비주기 함수도 주기가 ∞인 함수로 간주
② 주어진 governing equation으로부터 다음 식이 유도
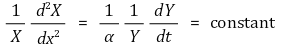
○ 좌변 : x에 대한 식 ↔ 우변 : y에 대한 식
○ X와 Y는 독립적이므로 좌변 = 우변 = constant
○ 경계조건
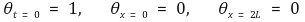
○ 경우 1. constant = λ2
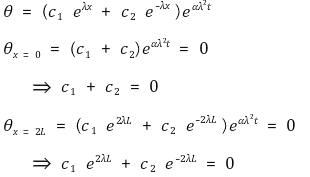
○ 경계조건으로부터 얻은 두 식은 일차독립이므로 해는 유일
○ c1 = c2 = 0인 해의 존재성이 확인
○ θ는 항등적으로 0 → 올바른 해가 아님
○ 경우 2. constant = - λ2
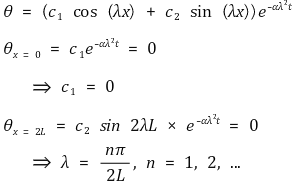
○ 이 식을 모든 n에 대해서 선형합으로 나타낼 수 있음
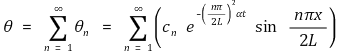
○ 시간에 대한 초기조건 이용
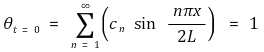
○ 양변에 sin mπx/2L을 곱한 뒤 0에서 2L까지 적분
○ (좌변)
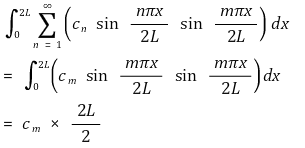
○ (우변)
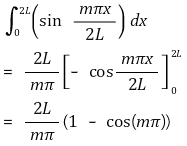
○ 결론
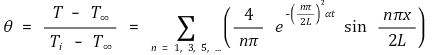
⑶ 문제 2. 반무한 고체(semi-infinite solid)
① 경우 1. t=0일 때, 전체 온도가 To로 등온인 경우
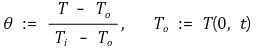
○ 반무한 고체의 면벡터가 x 방향과 나란할 때, y, z 축 방향으로는 대칭성을 가짐
○ 대단히 긴 막대나 전선 같은 무한한 길이의 막대로 간주할 수 있음
○ 문제 1에서 다룬 결과를 이용할 수 있음
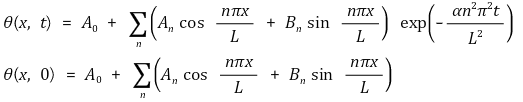
○ 이때 각 계수는 다음과 같이 정의
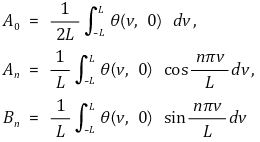
○ 푸리에 급수는 다음과 같이 변형
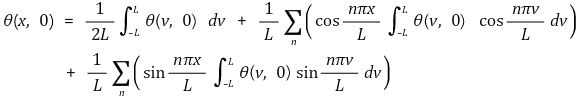
○ wn = nπ/L, Δwn = π/L
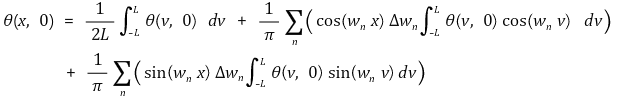
○ L을 ∞으로 극한 : 우변의 첫항은 0으로 수렴. 나머지 항은 다음과 같이 변형
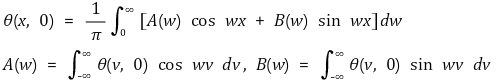
○ 위와 같이 적분으로 표현한 이유 : 비주기함수까지도 푸리에 급수를 적용하기 위함
○ 경계조건
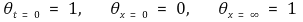
○ 이를 위에서 얻은 식에 대입
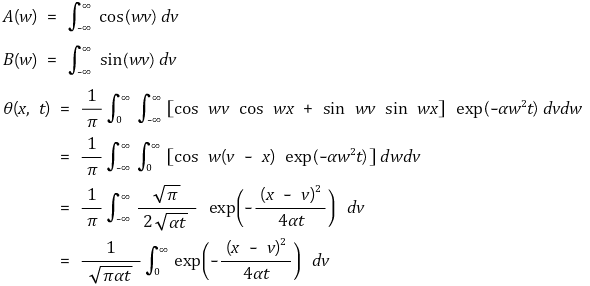
○ 결론
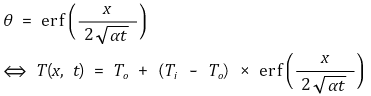
○ 표면온도 To가 등온인 경우 임의의 시간, 임의의 지점의 온도를 알 수 있음
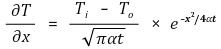
○ 열유속
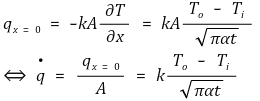
② 경우 2. 일정한 열유속이 주어질 때
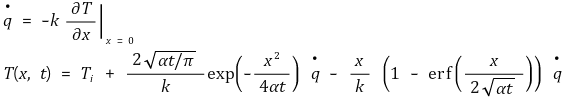
③ 경우 3. 일시적인 에너지 펄스가 주어질 때
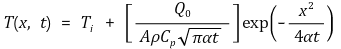
○ 특정 점에서의 열 전달율
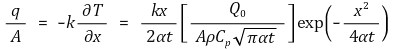
○ 경우 2와 달리 이 경우 시간이 지날수록 원래 상태로 돌아오려고 함 : 신호가 죽음(die)
④ 경우 4. 반무한 고체가 대류환경에 노출돼 있을 때
○ 경계조건
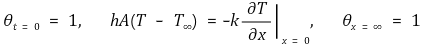
○ 기존의 Fo 뿐만 아니라 h, k에 관한 변수가 추가적으로 요구
⑤ 거리에 따른 온도 및 열량 그래프
○ Figure 4-4. (a)는 표면 온도가 일정할 때, (b)는 일정 열유속이 주어질 때
○ Figure 4-5. 갑자기 대류환경에 노출된 반무한고체


4. Hisler chart
⑴ 두께 2L을 가지는 무한 평면
① 중심 온도(center temperature)

② 비중심 온도(off-center temperature)

③ 시간 t 동안의 열 손실
○ Q0란 최대 손실 에너지량(즉, t = ∞까지의 에너지 손실량)을 의미

② 반지름이 r0인 무한한 길이의 원기둥
○ 중심 온도(center temperature)

② 비중심 온도(off-center temperature)

③ 시간 t 동안의 열 손실
○ Q0란 최대 손실 에너지량(즉, t = ∞까지의 에너지 손실량)을 의미

⑶ 반지름이 r0인 구
① 중심 온도(center temperature)

② 비중심 온도(off-center temperature)

③ 시간 t 동안의 열 손실
○ Q0란 최대 손실 에너지량(즉, t = ∞까지의 에너지 손실량)을 의미
○ 일반적으로 Q0 = mCP (Ti - T∞)로 계산

4. 다차원 물체 분석 : Hisler chart의 확장 [목차]
⑴ 예 1. z 방향 무한 길이 bar
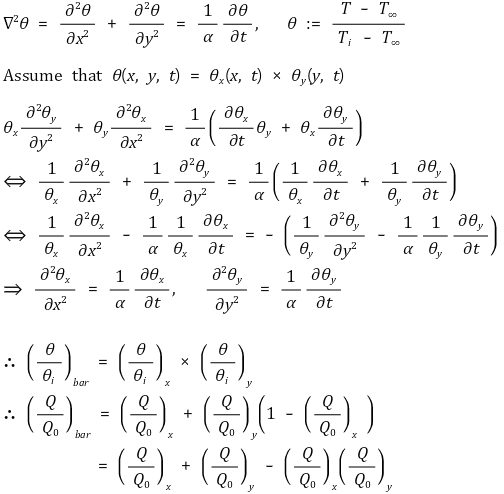
⑵ 예 2. semi-infinite cylinder
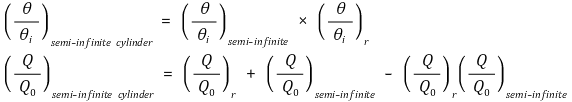
⑶ 예 3. short cylinder
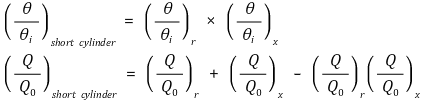
⑷ 예 4. rectangular parallel pipe
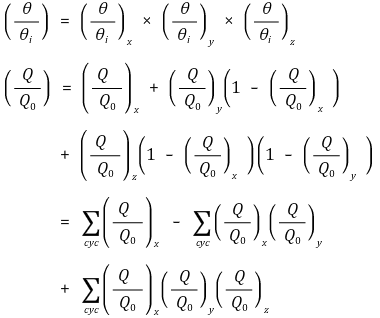
5. 수치해석적 방법 [목차]
⑴ 개요
① 유한차분법(FDM, finite difference method)을 이용 : 2D 물체에서 주로 이용
② 실제로 열전달 해석에 있어 대부분 수치해석이 사용됨
⑵ 직교좌표계 수치해석
① 지배 방정식(governing equation), 라플라스 방정식(Laplace equation)
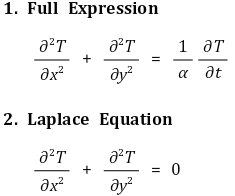
② 전방 일차 차분근사식
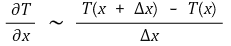
③ 후방 일차 차분근사식
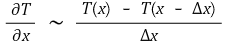
④ 중앙 일차 차분근사식
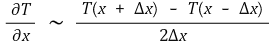
⑤ 시간 일차 차분근사식 : P번째 턴의 온도 TP, t = P × Δτ에 대해
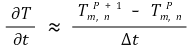
⑥ 이차 차분근사식

⑦ 내부절점 : 오직 전도만 일어남

Figure. 12. 내부절점
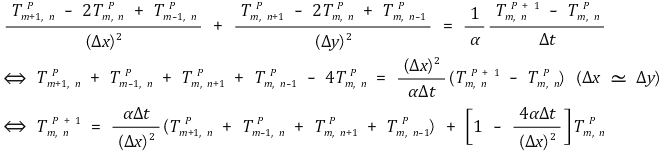
○ Δx와 Δt를 적당히 조절하면 다음과 같이 만들 수 있음
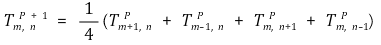
○ 위와 같은 과정으로 1D상에서도 식을 유도할 수 있음
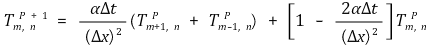
○ 안정성 확보(stability criteria)
○ 반복 계산에 있어 어떤 오류도 없어야 한다면 임의의 상황에 대해서 오류가 없어야 함
○ 아래 조건 이외의 node는 없다고 가정
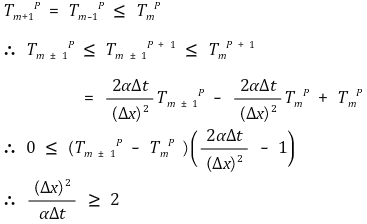
○ 2D 상에서도 비슷한 결론을 얻을 수 있음
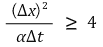
○ 직관적 의미 : t 방향으로 너무 빨리 증가하지 말아야 함
⑧ 표면절점 : 대류가 일어나는 경계면

Figure. 13. 표면절점
○ 전도로 전달된 에너지 + 대류로 전달된 에너지 = 내부에너지의 변화
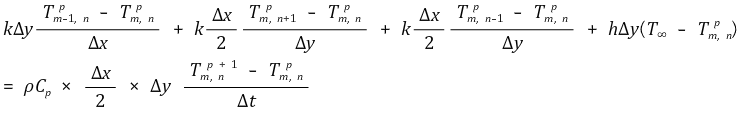
○ Δx = Δy임을 이용
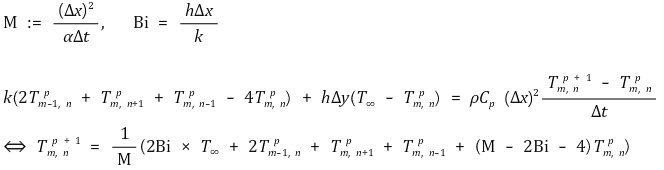
○ 안정성 확보(stability criteria)
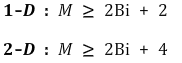
⑶ 원통좌표계 수치해석
① 지배방정식
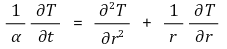
② 유한차분식 표현
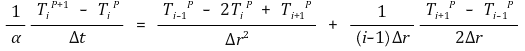
③ 중앙절점
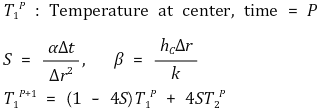
④ 내부절점
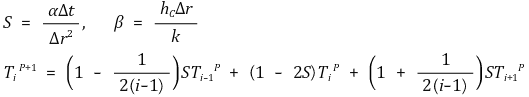
⑤ 표면절점
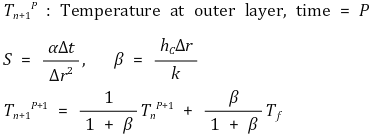
입력: 2016.04.17 13:52
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【열전달】 6강. 강제 대류계 (0) | 2016.06.27 |
|---|---|
| 【열전달】 5강. 대류의 원리 (5) | 2016.06.27 |
| 【열전달】 3강. 정상상태의 전도 2차원 (0) | 2016.06.27 |
| 【열전달】 2강. 정상상태의 전도 1차원 (0) | 2016.06.27 |
| 【열전달】 1강. 서론 (0) | 2016.06.27 |




최근댓글