2강. 정상상태의 전도 1차원(1D conduction in steady state)
추천글 : 【열전달】 열전달 목차
1. 정의 [본문]
2. 열전도도 [본문]
3. 열저항 [본문]
4. 열전도 일반식 [본문]
5. 열원계 [본문]
6. 핀 [본문]
1. 정의 [목차]
⑴ 특정 질점에서 온도 기울기가 있을 때 고온에서 저온으로 에너지가 흐르는 현상
⑵ 다음 식은 전류와의 유사성으로부터 유추된 식
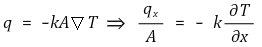
① k : 열전도도 [W/m·K 또는 W/m·℃]
② qx : x축 열전달율 [W]
③ A : 열전달 면적 [m2]
2. 열전도도(thermal conductivity) [목차]
⑴ 열전도도 k는 다음과 같은 관계식을 갖는다.

① n : 분자 수
② v : 분자의 속도
③ λ : 평균자유행로
④ 문제. 보온병의 구조는 일반적으로 내부벽과 외부벽의 사이가 진공으로 이루어져 있다. 그 이유를 간단히 설명하라.
⑤ 답.
○ 고체나 액체에 비해 기체의 열전도도는 낮음
○ 기체의 열전달은 분자운동에 의한 전도이므로 밀도에 비례, 진공에서 열전도는 완전히 차단됨
⑵ 기체(gases)
① 온도의 정의 : 분자의 평균 운동 에너지의 척도
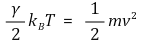
② 열전달 메커니즘
○ 1st. 빠른 분자(a)가 느린 분자(b)와 탄성충돌하면서 서로 속도를 교환
○ 2nd. 느려진 분자는 외부의 열을 공급받아 다시 빨라짐
③ 열전도도의 이론적 예측
○ 기체에 대한 kinetic theory에 의하면 이상기체의 경우 점도는 다음과 같이 유도됨
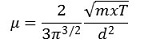
○ m : 기체 분자량
○ R : 기체상수
○ T : 절대온도
○ d : 기체분자의 지름
○ 이상기체의 경우 Cv = 1.5 R임
○ 따라서 열전도도는 다음과 같이 유도될 수 있음
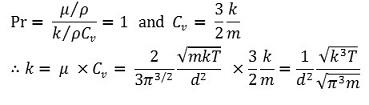
④ 열전도도의 실험적 측정 : 대류가 일어나지 않는 진공상태에서 측정 가능
⑤ k의 경향성
○ 온도 T가 커지면 속력 증가로 인해 충돌 빈도가 커져서 k 값이 커짐
○ 압력 P가 크면 nRT/V가 크다는 의미이므로, 이로 인해 k가 커짐
○ 분자량 Mw가 커지면 분자의 평균속도가 작아지면서 k가 작아짐
⑶ 액체(liquid)
① 대류가 일어나지 않는 진공상태에서 측정 가능
② 액체의 운동은 랜덤워크운동 뿐만 아니라 높은 밀도로 인한 분자간 상호작용으로 기체보다 복잡하다.
○ 다만 기체와 대체적으로 유사한 메커니즘이 적용되고, k의 경향성 또한 같다.
③ 물은 고체처럼 간주할 수 있어서(?) 비금속 액체 중에서 열전도도가 가장 크다.
⑷ 고체(solids)
① 열전도도는 electron component와 lattice component로 나뉜다.
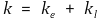
② electron component: 자유전자
○ 자유전자의 random한 운동으로 열이 전달된다.
○ Wiedemann Franz law
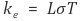
○ L : 로렌츠 숫자(Lorenz number)
○ σ : 전기전도도(electrical conductivity)
○ T : 절대온도
③ lattice component: 격자 진동 파동(lattice vibrational waves)
○ 1st. 결정격자를 구성하고 있는 원자는 절대 영도 이상이라면 항상 미약하게 열진동한다.
○ 2nd. 외부에서 열이 공급되면 열을 받은 원자는 더 크게 진동한다.
○ 3rd. 인접한 원자들은 전기적인 인력 혹은 척력으로 따라서 진동한다. (파동의 형태)
○ 4th. 맨 처음 진동하던 원자의 진동폭은 반대로 작아진다. (에너지 보존 법칙)
○ 위 메커니즘이 반복되서 열이 전달된다.
○ 격자의 밀도가 클수록, orderness가 좋을수록, 온도가 클수록 k가 커진다.
④ 예 1. 금속(metal)
○ 격자성분보다 자유전자성분이 훨씬 큼

○ 비교적 온도의 영향을 받지 않음
○ 불순물이 들어가면 자유전자의 이동에 방해가 생겨서 순수한 금속보다 k가 작다.
○ 온도 증가 → 원자의 진동 증가 → 전자의 운동 방해 → k의 증가율이 완화됨
⑤ 예 2. 비금속(non-metal)
○ 자유전자성분보다 격자성분이 훨씬 크다.

○ 비교적 온도의 영향을 많이 받음, 배열 정도와 밀도의 영향도 받음
○ 결정질 쿼츠의 k > 무결정질 유리의 k : 둘다 Si-O로 구성됨
○ 다이아몬드의 k > 그래핀의 k
○ 다이아몬드의 열전도도는 금속보다도 좋음
⑥ 단열(insulation)
○ 단열물질은 아래 크기 비교에서 뒤에 오는 것들을 사용 : 순금속 > 합금 >비금속 고체 > 액체 > 기체
○ fiber, powder, flake 타입의 물질은 밀도를 줄이므로 열전도도가 비교적 낮음
○ 기체가 차 있는 공간을 진공으로 만들면 열전도율이 0
⑸ 다양한 물질들의 열전도도
① 다양한 물질들의 열전도도
② 기타 물질
○ 석면(asbestos) : 0.166 W/m·℃
○ 벽돌 : 0.69 W/m·℃
○ 스테인리스강판 : 16 W/m·℃
○ 스티로폼 : 0.03316 W/m·℃
3. 열저항 (thermal resistance) [목차]
⑴ 무한 평면의 전도 열저항 (conductive thermal resistance - infinite plane)
① 가로, 세로가 두께에 비해 충분히 길면 ∇T의 방향은 두께 방향(z 축)임을 알 수 있다.
② 수식화
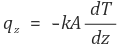
steady state에서는 qz의 값이 상수임을 알 수 있다.
따라서 dz를 이항하고, 양변을 적분하면 다음 식을 얻을 수 있다.
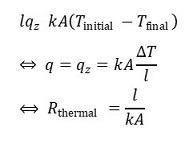
③ 직렬연결
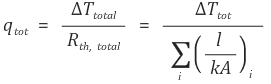
④ 병렬연결
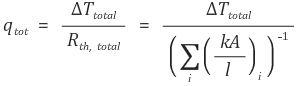
⑤ 단열성능 R-value
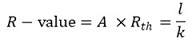
⑵ 실린더의 전도 열저항 (Conductive thermal resistance - cylinder)
① 수식화
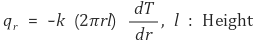
steady state에서는 qr의 값이 상수임을 알 수 있다.
따라서 좌변을 r에 대한 식으로 만들고 양변을 적분하자.
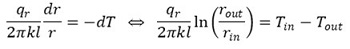
그러므로 q는 다음과 같다.
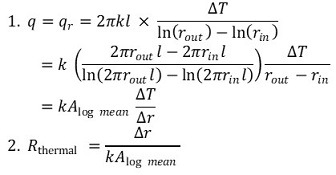
② 직렬연결
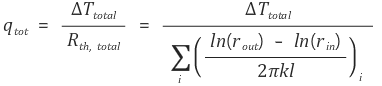
③ 병렬연결
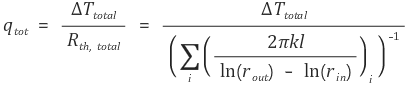
⑶ 구의 전도 열저항 (Conductive thermal resistance - sphere)
① 수식화
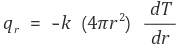
steady state에서는 qr의 값이 상수임을 알 수 있다.
따라서 좌변을 r에 대한 식으로 만들고 양변을 적분하자.
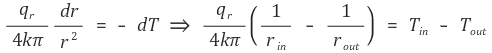
그러므로 q는 다음과 같다.

② 직렬연결
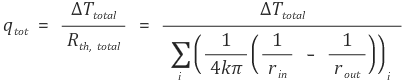
③ 병렬연결
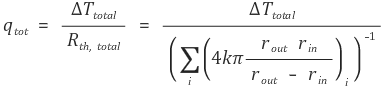
⑷ 대류 열저항 (Convective thermal resistance)
① 수식화

② 단열성능 R-value
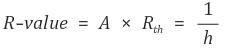
⑸ 무한평면의 총괄 열전달 계수 (Overall heat coefficient - infinite plane): U로 표기
① 가로, 세로가 두께에 비해 충분히 길면 ∇T의 방향은 두께 방향(z 축)임을 알 수 있다.
② 수식화
Rconvection, initial, Rcoduction, Rconvection, final의 직렬연결을 고려한다.
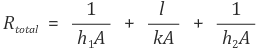
그러므로 q는 다음과 같다.
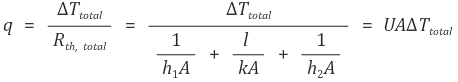
③ 단열성능 R-value
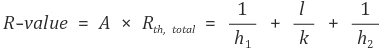
⑹ 속이 빈 실린더의 총괄 열전달 계수 (Overall heat coefficient - hollow cylinder) (ex. heat exchanger)
Figure. 1. 속이 빈 실린더의 총괄 열전달 계수
Rconvection, initial, Rcoduction, Rconvection, final의 직렬연결을 고려한다.
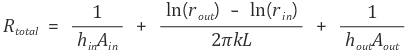
그러므로 q는 다음과 같다.
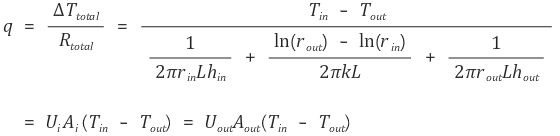
⑺ 단열 임계 두께
전도 열저항과 대류 열저항을 무시할 수 있는 매우 얇은 파이프 안으로 뜨거운 유체가 흐른다고 가정하자.
굳이 무시하지 않아도 논의의 최종 결과는 동일하다.
이때 파이프를 둘러싸는 절연물질의 종류는 바꿀 수 없다.
그 두께 (r2 - r1)만을 조절할 수 있을 때, 바깥 반지름 r2를 어떻게 정할지 고려하는 것이 문제이다.
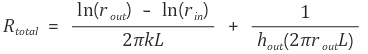
따라서 q는 다음과 같다.
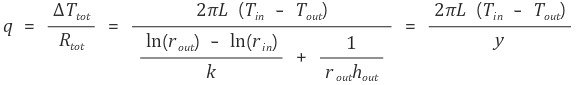
y에 대한 미분을 통해서 y의 최솟값을 알 수 있다.
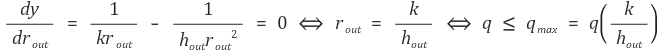
따라서 특정 두께 이하에서는 단열 물질을 사용하는 것이 오히려 부작용을 일으킨다는 것을 알 수 있다.
4. 열전도 일반식 [목차]
⑴ 1-D 기본
x = 0부터 x = L까지 x 축 상에 놓인 1차원 물체를 고려한다.정상상태 조건으로부터
qin = qout = q = constant가 유도된다.
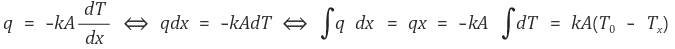
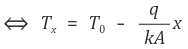
⑵ 1-D 일반화
단면이 무한한 판이고 길이가 dx인 특정 미소구간을 고려하자.
"유입된 에너지 + 미소구간에서 생성된 에너지 = 미소구간에 축적된 에너지 + 유출된 에너지"를 이용하자.
ⓐ 유입된 에너지 (per unit second)
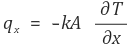
ⓑ 생성된 에너지 (per unit second)
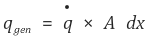
이때 (q˚)는 단위면적당 생성되는 에너지이다.
ⓒ 축적된 에너지 (per unit second)
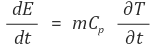
이때 열역학 제 1법칙(E = U + W)을 이용했다.
ⓓ 유출된 에너지
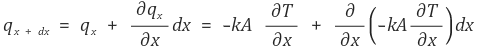
이때 다음과 같은 테일러 전개를 이용하였다.
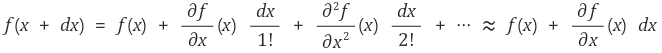
이제 ⓐ + ⓑ = ⓒ + ⓓ이라는 사실을 적용하자.
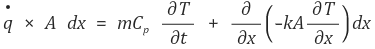
물질이 균일해서 모든 위치마다 성질이 같다고 하면 다음과 같다.
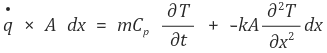
양변에 A dx를 나누자.
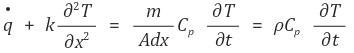
양변에 k를 나누면 다음과 같다.
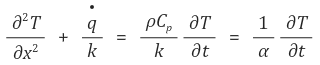
① 정상상태, 생성된 에너지 = 0
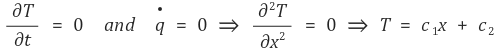
② 열확산도(thermal diffusivity)
○ α가 시간에 대한 함수. 단위 : ㎡/s
○ 수식화

○ α가 크다는 것은 k가 크거나 Cp가 작다는 뜻이다.
○ k가 큼 ⇔ 열전도율이 큼
○ Cp가 작음 ⇔ 더 많은 에너지 전달 ⇔ 물질의 온도를 높이는 데 흡수되는 에너지가 더 적음
⑶ 3-D 일반화
(x , y, z)를 기준으로 가로가 dx, 세로가 dy, 높이가 dz인 직육면체 미소구간을 고려하자.
⑵를 참고하면 다음과 같은 식을 찾을 수 있다.
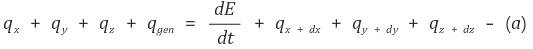
그리고 qi와 qi + di를 나타낼 수 있다.
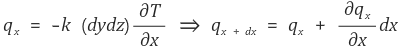
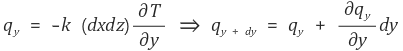
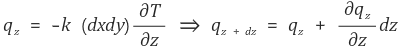
미소구간에서 생성된 에너지는 다음과 같다.
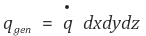
이때 (q˚)는 단위면적당 생성되는 에너지이다.
또한 축적된 에너지는 다음과 같다.
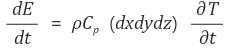
이제 (a) 식을 적용하자.
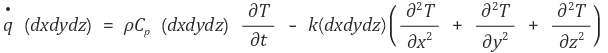
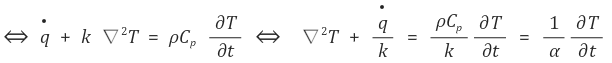
① 정상상태, 생성된 에너지 = 0
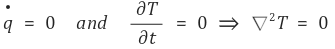
② 원기둥 좌표계(cylindrical coordinates)
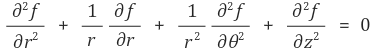
③ 구좌표계(spherical coordinates)
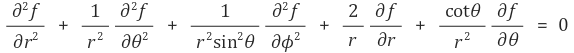
5. 열원계 (Heat source system) (예 : 전열(electric heating), 발열 화학반응(exothermic reaction)) [목차]
⑴ 가정
① 균질성 : 각 질점이 동일한 크기의 열을 생성(homogeneous heat source)
② 열전도도 k가 온도에 따라서 그렇게 크게 변동하지 않음
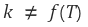
⑵ 무한 평면(infinite plane wall), 1-D, steady state
① 가로, 세로가 두께에 비해 충분히 길면 ∇T의 방향은 두께 방향(z 축)임을 알 수 있다.
② 경계 조건
○ T(± L) = Tw
○ T(0) = T0
③ 방법 1 : 위에서 유도한 결과를 사용한다.
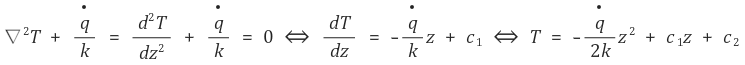
T(L) = T(-L)이므로 c1 = 0을 얻는다.
또한 T(0) = T0이므로 c2 = 0을 얻는다.
그러므로 다음 식을 얻을 수 있다.
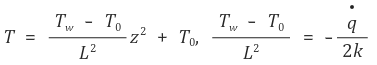
위 식을 다음과 같이 표현할 수도 있다.
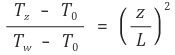
④ 방법 2 : 위에서 이용한 지배방정식(governing equation)을 단순화해서 처음부터 유도한다.
기본적인 발상은 다음 지배방정식을 이용하는 것이다.
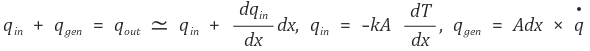
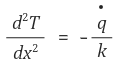
이 이후의 과정은 방법 1과 같다.
⑶ 실린더(cylinder), 1-D, steady state
① z축으로 길게 뻗어 있는 원기둥의 경우
θ와 z에 대한 변화율이 0이다.
② 경계조건
○ T(R) = Tw
○ T(0) = T0
③ 방법 1 : 위에서 유도한 결과를 사용한다.
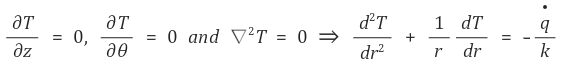
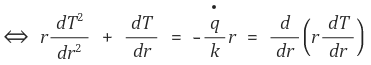

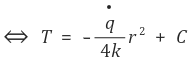
경계조건 5-⑶-①에 의하여 C의 값을 알 수 있다.
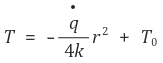
경계조건 5-⑶-①에 의하여 다음과 같이 표현할 수도 있다.
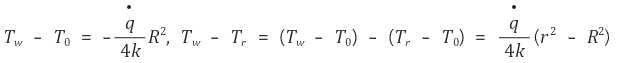
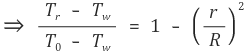
② 방법 2 : 위에서 이용한 지배방정식(governing equation)을 단순화해서 처음부터 유도한다.
기본적인 발상은 다음 지배방정식을 이용하는 것이다.
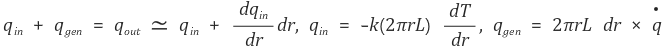
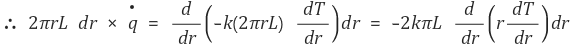
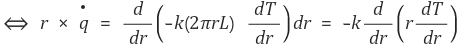
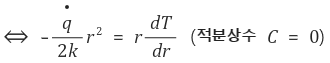
이후의 과정은 방법 1과 같다.
6. 핀(pin) (ex. 열 방출을 위한 CPU의 핀, hit sink, hit exchanger) [목차]
⑴ 전도와 대류를 동시에 고려한다. (conduction - convection system)
⑵ 수식화 (ver. 1)
Figure. 5. 모델링
우선 z 방향에 대한 온도 변화를 살펴보자.
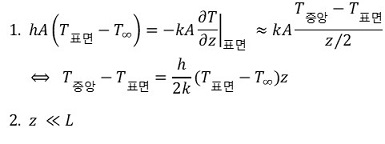
따라서 중앙에서의 온도와 z 축 끝, 표면에서의 온도가 거의 같음을 알 수 있다. 비슷한 논의를 t(thickness) 방향에 대해서도 말할 수 있다.따라서 ΔT 의 방향은 x축과 나란하다.위의 그림을 토대로 식을 세울 수 있다.
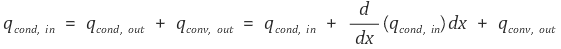
따라서
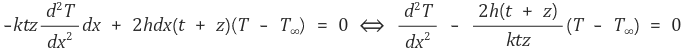
P(둘레, parameter)를 도입하면 다음 식을 얻을 수 있다.
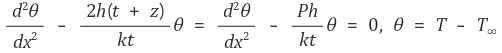
위 식은 제차 선형 상미방방정식이므로 쉽게 해를 구할 수 있다.
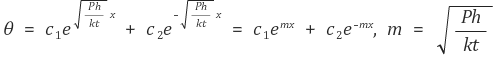
① 경계조건 case 1 (infinite): fin is very long
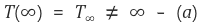
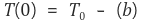
(a)에 의해 c1 = 0이고, (b)에 의해 c2 = T(0) = T0을 얻는다.
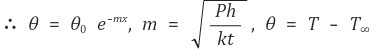
② 경계조건 case 2 (insulated) : the end of fin is insulated
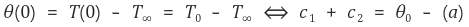
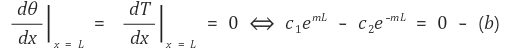
위 두 연립 일차방정식 (a), (b)를 풀면 다음을 얻을 수 있다.
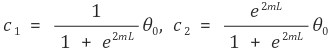
따라서 다음과 같이 정리할 수 있다.
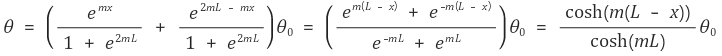
③ 경계조건 case 3 (real) : the finite fin length
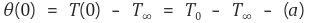
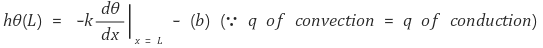
위 수식을 풀면 다음 결론을 얻는다.
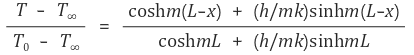
위와 같은 방법으로 계산하면, 계산량이 매우 많아진다.따라서 계산을 단순화할 필요가 있다.
Figure. 6. 모델링
단, 다음 식이 성립한다고 가정한다.
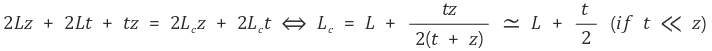
왼쪽의 노란색 면에서의 ΔT와 오른쪽의 노란색 면에서의 ΔTavg가 서로 비슷하다고 볼 수 있다.
(그리고 면의 넓이는 서로 같다.)
그런데 오른쪽 그림에서 x = L인 지점에서 전도로 나가는 열은 바로 노란색 면으로 나가는 열과 같다.
따라서 왼쪽 그림과 오른쪽 그림은 같은 상황이다.
이제 6.2.2.의 풀이를 적용할 수 있다.
이러한 케이스 전환에 대한 오차는 다음과 같이 나타낼 수 있다.
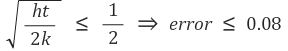
④ fin을 통한 전체 열 전달율 (total heat transfer rate through fins)
○ 가장 처음 전도를 통해 들어오는 열의 양
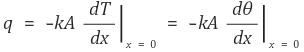
○ 모든 대류면을 통해서 나가는 열의 양
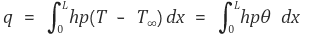
○ 경계조건 case 1에서의 총 열전달률
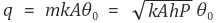
○ 경계조건 case 2에서의 총 열전달률
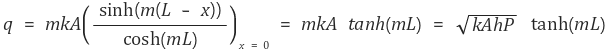
○ 경계조건 case 3에서의 총 열전달률
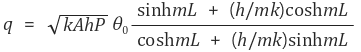
⑶ 수식화 (ver. 2)
사각형 단면을 갖는 원주형 핀(circumferential fin)이 지름 d인 튜브에 설치되어 있다.
핀의 재질은 k이고, 두께는 t, 핀의 외부 반지름은 R이다.
튜브의 온도는 Tw를 유지하고 있으며, T∞ 및 대류 열전달 계수가 h인 환경에 놓여 있다.
만약 t가 R에 비해 굉장히 작다면 ∇T의 방향이 중심으로부터 방사 방향임을 알 수 있다.
그러면 다음과 같은 식을 찾을 수 있다.
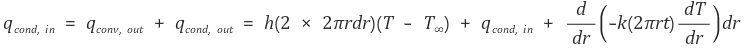
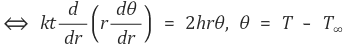
그리고 경계조건은 다음과 같다.
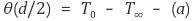
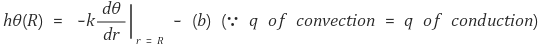
그러나 위와 같은 함수는 Bessel 함수로 더이상 전개하기는 어렵다.
따라서 이미 수치해석적으로 나와 있는 값을 사용하는 것이 일반적이다.
이미 나와 있는 값은 끝이 단열 조건인 경우가 많아서 R 대신 Rc를 사용한다.
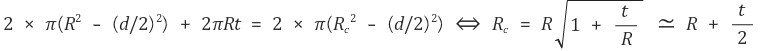
이때 6-⑵에서 했던 근사를 했다.
⑷ 수식화 (ver. 3)
⑵와 같은 핀을 생각한다.
이 핀이 대류가 무시될 수 있는 진공 안에 놓여 있으며 복사에 의해 열손실이 일어난다.
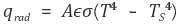
여기서 ε는 방사도, σ는 Stefan-Boltzmann 상수이다.
x에 관한 함수로 표현되는 핀의 온도에 대한 미분방정식을 구하자.우선 기본 방정식은 다음과 같다.
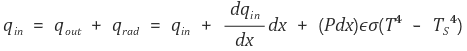
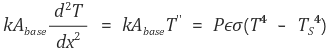
위 식의 양변에 T'을 곱하자.
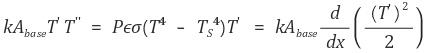
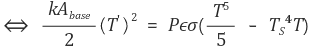
이 식의 해는 일반적으로 풀 수 없고, 수치해석으로만 접근할 수 있다.
⑸ fin의 성능
① efficiency(효율성)
○ 수식화
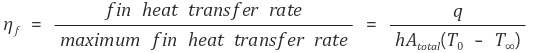
○ fin의 열전달률을 구하는 방법
○ 첫째, 다음을 계산한다.
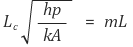
○ 둘째, mL - ηf 그래프를 읽어서 ηf을 구한다.
○ Ap는 단면의 넓이(profile area), Lc는 핀의 길이이다. (단, 핀은 끝이 단열된 상태)
○ 직육면체꼴 핀의 경우 다음과 같은 함수가 된다.
○ 셋째, 최대 열전달률 qmax를 계산한다.
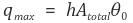
○ 넷째, fin의 효율의 정의를 통해 열전달을을 계산할 수 있다.
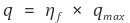
② effectiveness(효과성)

입력: 2016.03.21 18:34
'▶ 자연과학 > ▷ 유체역학·전달현상' 카테고리의 다른 글
| 【열전달】 5강. 대류의 원리 (5) | 2016.06.27 |
|---|---|
| 【열전달】 4강. 비정상상태의 열전도 (3) | 2016.06.27 |
| 【열전달】 3강. 정상상태의 전도 2차원 (0) | 2016.06.27 |
| 【열전달】 1강. 서론 (0) | 2016.06.27 |
| 【물리학】 유체역학 목차 (0) | 2016.06.26 |








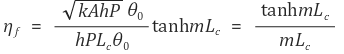
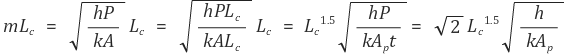






최근댓글