11강. 초월함수 (지수함수, 로그함수, 삼각함수)
추천글 : 【해석학】 해석학 목차
1. 지수함수와 로그함수 [본문]
2. 삼각함수 [본문]
1. 지수함수와 로그함수 [목차]
⑴ 자연상수(natural constant) : 네이피어 상수(Napier constant)라고도 함
① 무한급수 수열 xn의 존재성
○ xn에 대한 이항정리

○ 정리 1. xn은 단조증가함수

○ 정리 2. xn은 유계

○ 결론 : 완비성 공리에 의해 xn은 수렴함
② 자연상수 e의 정의
○ 자연수 범위에서의 정의
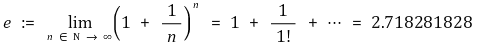
○ 양의 실수 범위에서의 정의
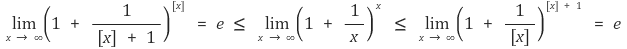
○ 음의 실수 범위에서의 정의
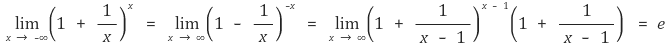
⑵ 지수함수(exponential function)
① 지수함수(exponential function)
○ a ∈ ℝ에 대해, a0 = 1으로 정의
○ a ∈ ℝ에 대해, an+1 = an × a에 의해 모든 0 이상의 정수 n에 대해 an을 정의
○ a ∈ ℝ, n ∈ ℕ에 대해
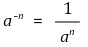
으로 정의
○ a ∈ ℝ, n ∈ ℕ, m ∈ ℤ에 대해

으로 정의
○ 밑이 a > 0, 지수가 x ∈ ℝ일 때 지수함수를 다음과 같이 정의

② 자연지수함수(natural exponential function) : 밑이 e인 지수함수
○ ex의 원점에서의 미분계수
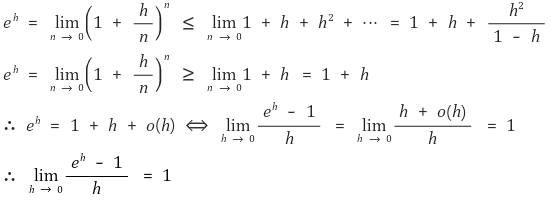
○ ex의 미분계수 : 도함수가 자기 자신과 같음
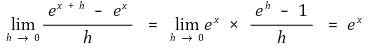
○ ex의 매클로린 급수(Maclaurin series)
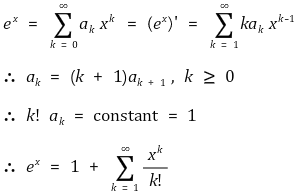
③ 지수함수의 성질
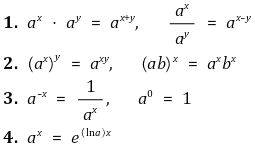
⑶ 로그함수(logarithmic function) : 지수함수의 역함수
① 정의 : 밑이 a이고 진수가 b, 지수가 y인 경우

② 성질
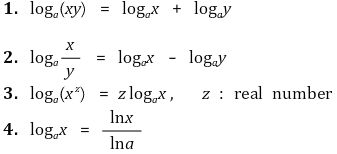
③ 자연로그(natural logarithms) : 밑이 e인 로그
④ 상용로그(common logarithms) : 밑이 10인 로그
⑷ 해석학적 정의
① 자연로그함수 : 함수 ℓ : (0, ∞) → ℝ을 다음과 같이 정의. ln x로도 표시함
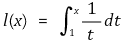
○ 정리 1. 로그함수는 전단사함수
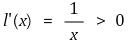
○ 정리 2. 각 a, b > 0에 대해 ℓ(ab) = ℓ(a) + ℓ(b)
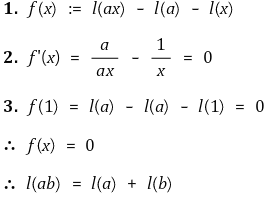
② 자연지수함수 : ℓ(x)의 역함수 k : ℝ → (0, ∞)를 지칭함. ex로도 표시함
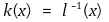
○ 정리 1. k'(x) = k(x)
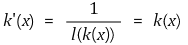
○ 정리 2. x, y ∈ ℝ에 대해 k(x+y) = k(x) × k(y)
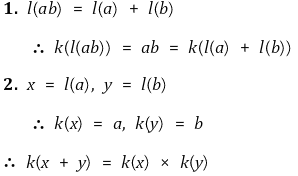
③ 지수함수
○ a > 0, x ∈ ℝ에 대해
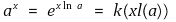
로 정의
○ a > 0, a ≠ 1이고 x > 0이면
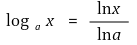
로 정의
○ 정리 1. a >0, x, y ∈ ℝ에 대해 ax+y = axay
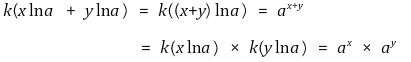
④ 로그함수
○ 정리 1. a >0, a ≠ 1, x > 0, y ∈ ℝ일 때
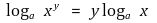
가 성립
○ 정리 2. a > 0, a ≠ 1, x > 0, y ∈ ℝ일 때 logax = y와 x = ay이 동치
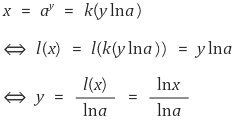
⑸ 지수함수 차수(exponential order)를 갖는 함수 : 어떤 M, γ > 0가 있어서 [0, ∞) 구간에서 다음을 만족하는 함수 f
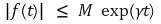
2. 삼각함수 [목차]
⑴ 정의
① 각의 표시 1. 육십분법 : 1회전각을 360°로 정의한 각의 표시법
② 각의 표시 2. 호도법(radian measure, circular measure) : θ = ℓ / r
③ 삼각함수의 정의
○ 사인 함수(sine function) : 호도법으로 표시한 반시계 방향의 각도 θ에 대해 y 좌표를 sin θ로 표시함
○ 코사인 함수(cosine function) : 호도법으로 표시한 반시계 방향의 각도 θ에 대해 x 좌표를 cos θ로 표시함
○ 탄젠트함수(tangent function) : tan θ ≡ sin θ / cos θ
○ 코시컨트 함수(cosecant function) : csc θ ≡ 1 / sin θ
○ 시컨트 함수(secant function) : sec θ ≡ 1 / cos θ
○ 코탄젠트 함수(cotangent function) : cot θ ≡ cos θ / sin θ
④ 삼각함수의 역함수 정의
○ 아크사인 함수(arcsine function) : arcsin θ ≡ sin-1 θ
○ 아크코사인 함수(arccosine function) : arccos θ ≡ cos-1 θ
○ 아크탄젠트 함수(arctangent function) : arctan θ ≡ tan-1 θ
⑵ 삼각함수의 기본 성질
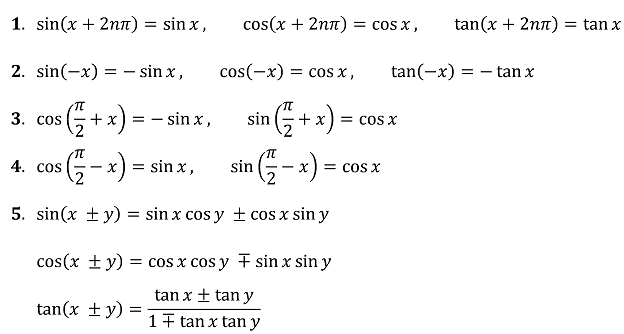
⑶ 삼각함수의 변환
① 곱을 합과 차로 바꾸기
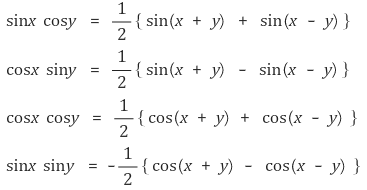
② 합 또는 차를 곱으로 바꾸기
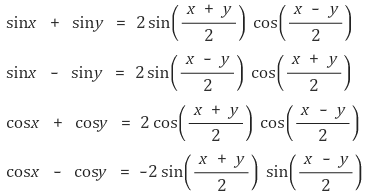
③ 배각공식과 반각공식
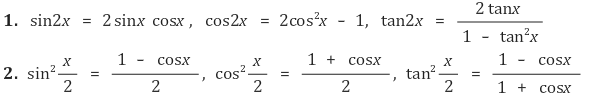
⑷ 삼각함수 관련 법칙
① 사인법칙 : ΔABC의 외접원의 반지름을 R, 각의 대응변의 길이를 a, b, c라 할 때 다음이 성립
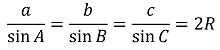
② 삼각형의 면적과 사인법칙 : ΔABC의 각의 대응변의 길이를 a, b, c라 할 때 다음이 성립
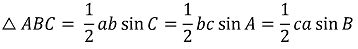
③ 제1코사인법칙 : ΔABC의 각의 대응변의 길이를 a, b, c라 할 때 다음이 성립
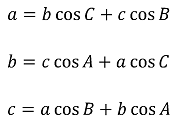
④ 제2코사인법칙 : ΔABC의 각의 대응변의 길이를 a, b, c라 할 때 다음이 성립
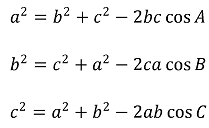
⑤ 헤론의 공식(Heron's formula) : 삼각형의 세 변의 길이를 각각 a, b, c라 하면 넓이는 다음과 같음
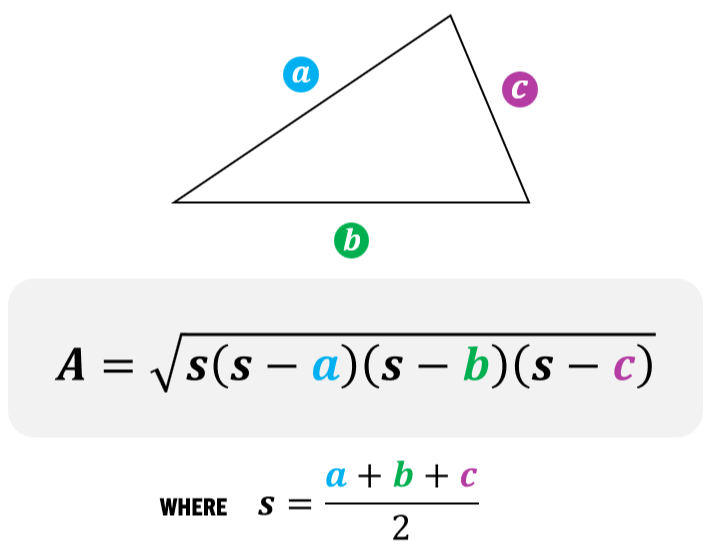

⑥ 유용 암기 공식 : 부분함수법(integration by parts)으로 증명 가능
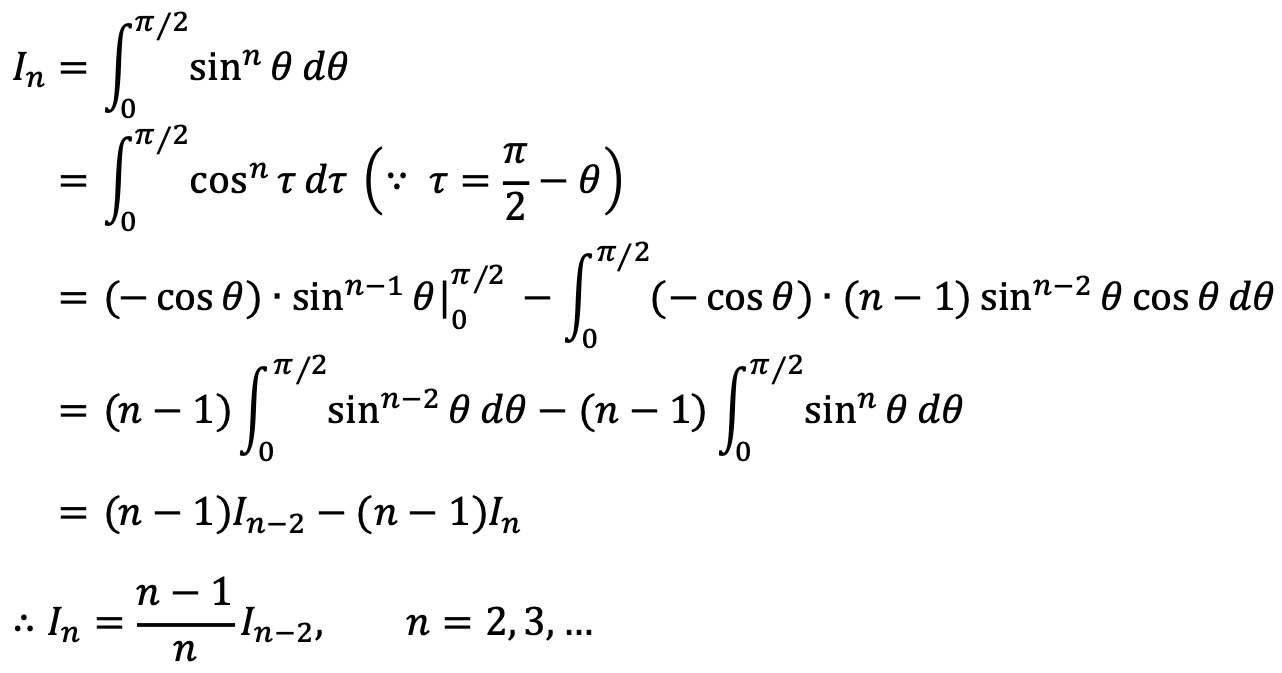
⑦ 코사인의 수열합
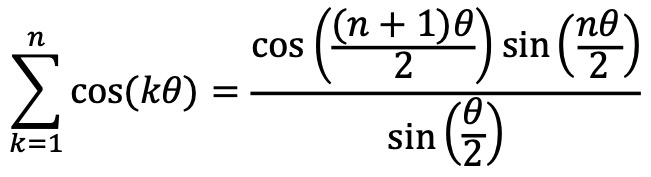
○ 증명 1. 복소수 지수함수의 등비수열

○ 방법 2. 수학적 귀납법
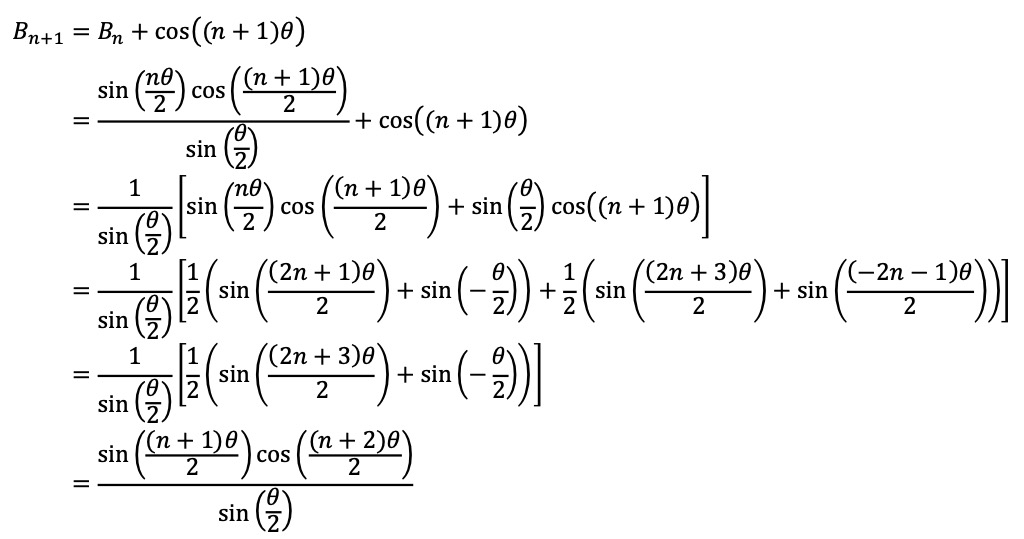
입력: 2020.03.19 09:47
수정: 2023.08.03 23:27
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 20강. 푸리에 급수 (0) | 2020.01.17 |
|---|---|
| 【해석학】 19강. 무한급수의 수렴판정법 (2) | 2020.01.17 |
| 【해석학】 18강. 케플러 1, 2, 3법칙 증명 (28) | 2020.01.11 |
| 【해석학】 17강. 사이클로이드 (2) | 2020.01.11 |
| 【해석학】 16강. 가우스 발산정리 (0) | 2020.01.11 |




최근댓글