19강. 무한급수의 수렴판정법
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 각 항이 0인 무한합 [본문]
2. 비교, 근호 판정법 [본문]
3. 교대무한합 [본문]
4. 테일러 급수 전개 [본문]
5. 무한차 다항식 [본문]
1. 각 항이 0인 무한합 [목차]
⑴ 예제 : 함수 f : [1, ∞) → (0, ∞)가 감소한다고 하자. 이때 무한합
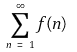
이 수렴할 필요충분조건은 무한적분
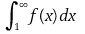
가 존재하는 것과 같음을 보이시오.
⑵ 예제 : 어떠한 실수 p에 대해 무한합

이 수렴하는가?
① p > 1 : 수렴. 다음 적분 부등식을 이용
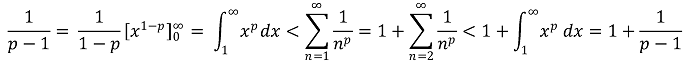
② p = 1 : 발산. 조화수열의 발산
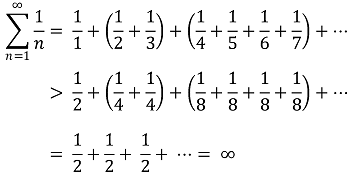
③ p < 1 : 발산.
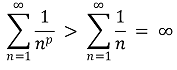
⑶ 예제 : 0 ≤ an ≤ bn이 n = 1, 2, 3, ···에 대해 성립한다고 하자. 이때 무한합
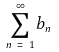
이 수렴하면 무한합
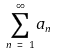
도 수렴함을 보이시오.
⑷ 예제 : 무한합
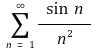
은 수렴하는가?
2. 비교, 근호 판정법 [목차]
⑴ 예제 : 각 n ∈ ℕ에 대해 an > 0이고
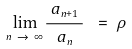
이 존재한다고 하자. 이때 ρ < 1이면 무한합
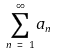
은 수렴하고, ρ > 1이면 무한합
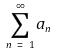
은 수렴하지 않는다.
⑵ 예제 : 무한합
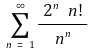
은 수렴하는가?
⑶ 예제 : 각 n ∈ ℕ에 대해 an ≥ 0이고
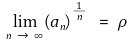
이 존재한다고 하자. 이때 ρ < 1이면 무한합
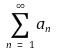
은 수렴하고, ρ > 1이면 무한합
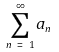
은 수렴하지 않음을 보이시오.
⑷ 예제 :
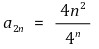
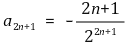
일 때 무한합

은 수렴하는가?
⑸ 예제 : 무한합
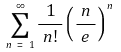
은 수렴하는가?
⑹ 예제 : τ(n)을 자연수 n의 양의 약수의 개수라고 하면 어떤 실수 x에 대해 무한합
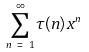
이 수렴하겠는가?
3. 교대무한합 [목차]
⑴ 예제 : 각 n ∈ ℕ에 대해 an > 0이고 a1 ≥ a2 ≥ ···이며
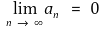
이라 하자.
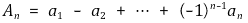
이라 할 때 다음을 보이시오.
①
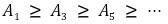
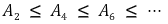
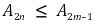
② 무한합

이 수렴하며 각 n에 대해
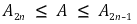
이다. 특히
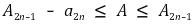

이 성립한다.
4. 테일러 급수 전개 [목차]
⑴ 주요 함수의 테일러 급수 전개
⑵ 예제 : 각 |x| < 1에 대해

을 보이시오.
⑶ 예제 : 모든 실수 x에 대해

이 성립함을 보이시오.
⑷ 예제 : 다음의 식
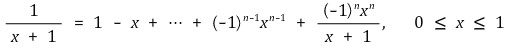
으로부터 양변을 적분하여

을 보이시오.
풀이.
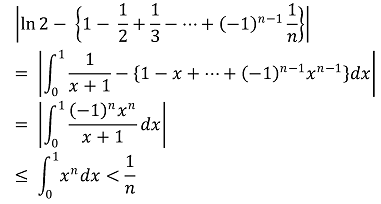
⑸ 예제 :
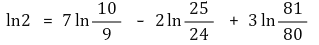
을 보이시오. 이제 ln 2의 값을 소수 셋째자리까지 구하시오.
5. 무한차 다항식 [목차]
⑴ 양수 R과 실수 a0, a1, ···, an, ···가 있어 각 |x| < R에 대해 무한합
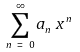
이 수렴한다고 하자. 이때
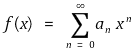
로 함수 f : (-R, R) → ℝ를 정의할 수 있다. 이 함수 f는 무한합으로 정의된 함수이다. 혹은 무한차 다항식이다.
⑵ 예제 : 양수 R과 수열 a0, a1, ···, an, ···, 그리고 함수 f가 위와 같다고 하자. 이때 함수 f는 연속이다.
⑶ 예제 : 양수 R과 수열 a0, a1, ···, an, ···, 그리고 함수 f가 위와 같다고 하자. |x| < R이면 무한합
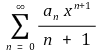
이 수렴하고

임을 보이시오.
⑷ 예제 : 양수 R과 수열 a0, a1, ···, an, ···, 그리고 함수 f가 위와 같다고 하자. 각 |x| < R에 대해 f가 x에서 미분가능하고 무한합
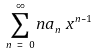
이 수렴하여
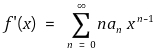
이 성립함을 보이시오.
⑸ 예제 : 무한합
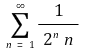

의 수렴값을 구하시오.
⑹ 예제 : 적분
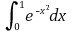
의 값을 소수 둘째자리까지 구하시오.
⑺ 예제 : f(x) = tan x : (-π/2, π/2) → ℝ는 미분가능하고 전단사함수이다. 따라서 그 역함수 g(x) = tan-1 x : ℝ→ (-π/2, π/2)이 존재한다. g의 도함수를 구하시오. tan-1 x를 무한차 다항식으로 나타낼 수 있는가?
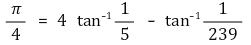
를 보이고 π의 값을 소수 둘째자리까지 구하시오.
입력 : 2020.01.17 00:59
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 21강. 미분방정식의 해의 존재성 (0) | 2020.01.18 |
|---|---|
| 【해석학】 20강. 푸리에 급수 (0) | 2020.01.17 |
| 【해석학】 11강. 초월함수 (지수함수, 로그함수, 삼각함수) (0) | 2020.01.16 |
| 【해석학】 18강. 케플러 1, 2, 3법칙 증명 (28) | 2020.01.11 |
| 【해석학】 17강. 사이클로이드 (2) | 2020.01.11 |





최근댓글