군 이론(Group Theory)
추천글 : 【현대수학】 현대수학 목차
1. 군 이론 [본문]
2. 함수 [본문]
a. 유한 순환군(아벨군)은 궁극적으로 cos이나 sin으로 표현된다
1. 군 이론 [목차]
⑴ 공리(axiom)
① 폐포(closure) : ∀a, b ∈ G, a·b ∈ G
② 결합법칙(associative property) : ∀a, b, c ∈ G, (a·b)·c = a·(b·c)
③ 항등원(identity element) : 임의의 a ∈ G에 대하여, a·e = e·a = a를 만족하는 e ∈ G가 존재함
④ 역원(inverse element) : 임의의 a ∈ G에 대해 a·a-1 = a-1·a = e인 a-1이 존재함
○ 역원의 유일성 : 임의의 두 역원 a0-1, a1-1을 잡을 때 언제나 a0-1 = a1-1이 성립함
○ a0-1 = e·a0-1 = (a1-1·a)·a0-1 = a1-1·(a·a0-1) = a1-1·e = a1-1
⑵ 용어
① 준동형사상(homomorphism) : 두 군 (G, ·), (H, *)이 주어져 있을 때, ρ(u · v) = ρ(u) * ρ(v)를 만족하는 사상 ρ : G → H
② 동형사상(isomorphism) : 일대일 대응(bijective)을 만족하는 homomorphism
③ 곱셈 군(product group) : 두 군 G, H의 군에서의 카테시안 곱 G × H로 정의됨 (e.g., (g1, h1))
○ 새로운 군 연산은 (g1, h1)·(g2, h2) = (g1g2, h1h2)
④ 교환법칙(commutativity) : 그룹 (G, +)이 연산의 순서가 중요하지 않을 때, 즉 a·b = b·a일 때, 교환 가능(commutative) 또는 아벨 그룹(Abelian)이라고 함
○ 군의 모든 원소에 대해 이 성질이 성립하지 않을 경우, 그 군은 비교환 군(non-commutative)이라고 함
○ 유한한 교환군은 각각 순환군(cyclic group)의 곱으로 표현될 수 있음
⑤ 군의 작용(group action) : 군의 작용은 T : G × X → X로 정의되는 함수로, (g, x) 쌍을 X의 원소로 사상
○ 조건 1. G의 항등원 e에 대하여 T(e, x) = x
○ 조건 2. g1, g2 ∈ G에 대하여 T(g1, T(g2, x)) = T(g1g2, x)
○ 간단히 표현하기 위해 T(g, x)를 Tg(x)로 나타내며, 이는 점 x가 gx (= Tg(x))로 사상된다고 표현함
⑥ 불변성(invariance) : 함수 ϕ : X → Y가 G-불변성을 가지려면, 모든 g ∈ G와 x ∈ X에 대해 ϕ(x) = ϕ(gx)를 만족해야 함
○ 이는 입력 공간에 대한 군의 작용이 출력에 아무런 영향을 미치지 않는다는 것을 의미
⑦ 등변성(equivariance) : 함수 ϕ : X → Y가 G-등변성을 가지려면, 모든 g ∈ G와 x ∈ X에 대해 ϕ(gx) = g'ϕ(x)를 만족해야 함
○ 이때 g' ∈ G'은 G와 homomorphic이면서 출력 공간에 작용하는 군
○ 등변성은 입력 공간에서의 군 작용이 출력 공간에서 대응되는 군 작용을 초래한다는 것을 의미함
⑧ 궤도(orbit) : 점 x ∈ X에 대해, x의 궤도 Gx는 집합 {gx : g ∈ G}로 정의됨
○ 예를 들어, G가 translation 군이고 x가 이미지라면, 궤도는 해당 이미지의 모든 이동된 버전을 의미함
⑨ 균질 공간(homogeneous space) : 임의의 페어 x1, x2 ∈ X에 대하여 gx1 = x2인 g ∈ G가 언제나 존재하는 공간 X
○ 군 G의 작용을 갖춘 균질 공간 X를 G-공간(G-space)이라고도 함
⑩ 표현(representation) : 군 G의 표현은 벡터 공간 V 위로의 선형변환군 GL(V)에 대해 사상 ρ : G → GL(V)을 의미함
○ homomorphism 조건 : 표현은 추가로 ρ(g1g2) = ρ(g1)ρ(g2)를 만족해야 함
○ 많은 경우 V는 ℝn 또는 ℂn
○ 가약(reducible) : 표현을 다른 표현들의 direct sum으로 분해할 수 있는 경우
○ 불가약(irreducible) : 가약 표현이 아닌 모든 표현. 불가약 표현들의 집합을 Irr(G), irreps 등으로 표현
○ 유한 교환 그룹(finite commutative group)의 불가약 표현들은 모두 1차원이며 그룹 자체와 일대일 대응(bijection)을 이룸
○ 유한 교환 그룹의 불가약 표현들은 순환 그룹 ℤ/nℤ의 곱으로 분류됨
⑶ 정리 1. 군 〈G, *〉의 각 공리들은 〈G, *〉의 structural property임
① 정의 : 〈G, *〉의 structural property란, 〈G, *〉와 isomorphic한 모든 binary structure가 공유하는 특성을 의미함
② 전제 : isomorphism φ : G → S를 통해 〈S, ㆍ〉는 〈G, *〉와 isomorphic한 binary structure임
③ 공리 1에 대한 증명 : α, β, γ ∈ S, ∃ a, b, c ∈ G s.t. φ(a) = α, φ(b) = β, φ(c) = γ

④ 공리 2에 대한 증명
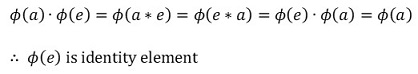
⑤ 공리 3에 대한 증명 : a ∈ G의 역원 a'에 대하여,
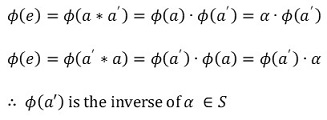
2. 함수 [목차]
⑴ 단사함수(injective, one-to-one) : 함수 f: X → Y에서 치역의 원소마다 정의역의 오직 하나의 원소만이 관계를 가질 때 그 함수
⑵ 전사함수(surjective, onto) : 공역 = 치역인 함수
⑶ 전단사함수(bijective) : 단사함수이면서 전사함수인 함수
입력: 2021.03.27 22:54
수정: 2024.12.21 15:42
'▶ 자연과학 > ▷ 현대수학' 카테고리의 다른 글
| 【현대수학】 그래프 이론 (Graph Theory) (2) | 2024.10.02 |
|---|---|
| 【현대수학】 현대수학 목차 (0) | 2016.06.25 |
| 【현대수학】 수학 난제 리스트 (0) | 2016.06.24 |



최근댓글