제 43회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 43회 전국 대학생 수학경시대회
제 2 분야
2025년 11월 1일 (10:30 - 13:00)
1. 다음 조건을 모두 만족하는 미분가능한 이변수함수 f : ℝ2 → ℝ가 주어져 있다.
f(0, 0) = 0, limt→0 f(t, t) / t = 2, limt→0 f(t, 2t) / t = -1
조건 a2 + b2 = 1을 만족하는 실수 a, b에 대하여 다음 극한이 가질 수 있는 최댓값과 최솟값을 구하여라.
limt→0 f(at, bt) / t
Solution.
방향미분을 활용해 푸는 문제이다.
∇f(0, 0)·v = Dvf(0, 0) = limt→0 ( f(tv) - f(0, 0) ) / t
∴ 2 = (∂f/∂x|x=0, ∂f/∂y|y=0) · (1,1), -1 = (∂f/∂x|x=0, ∂f/∂y|y=0) · (1, 2)
∴ ∂f/∂x|x=0 = 5, ∂f/∂y|y=0 = -3
limt→0 f(at, bt) / t = ∇f(0, 0) · (a, b) = 5a - 3b = 5 sin θ - 3 cos θ = √(52 + 32) sin(θ + α)
∴ (준식)의 최댓값은 √34, 최솟값은 -√34이다.
2. 다음 미분방정식의 해 f를 구하여라.
f''(x) + 2f'(x) + f(x) = 2x-2e-x, f(1) = f'(1) = 0
Solution.
g(x) := f'(x) + f(x), g(1) = 0
g'(x) + g(x) = 2x-2e-x ⇔ exg'(x) + exg(x) = 2x-2
∴ exg(x) = exf'(x) + exf(x) = -2x-1 + 2 (∵ g(1) = 0)
∴ exf(x) = -2 ln |x| + 2x - 2 (∵ f(1) = 0)
∴ f(x) = 2e-x(-ln |x| + x - 1)
3. 3차원 벡터 공간의 한 평면 위에 놓인 다섯 개의 점 A, B, C, D, E가 다음 조건을 모두 만족한다.
● |AB| = |BC| = |CD| = |DE| = |EA| = 1
● AB × BC = BC × CD = CD × DE = DE × EA = EA × AB ≠ 0
● AB·BC = BC·CD = CD·DE = DE·EA = EA·AB
⑴ 이때 CE는 AB의 상수배임을 보여라.
⑵ CE = kAB가 되도록 하는 상수 k의 가능한 값을 모두 구하고, 각각의 경우에 ABCDE는 어떤 도형인지 설명하여라.
Solution.
⑴
AB × CE
= AB × (AE - AC)
= AB × (AE - AB - BC)
= AB × AE - AB × BC
= -AB × EA - AB × BC
= EA × AB - AB × BC
= 0
∴ AB || CE
⑵
AB × BC = BC × CD이고 AB·BC = BC·CD이므로 ∠ABC = ∠BCD이다.
왜냐하면 sin ∠ABC = sin ∠BCD이고 cos ∠ABC = cos ∠ABC이기 때문이다.
따라서 AB → BC → CD → DE → EA가 되면서 일정한 각도로 회전함을 알 수 있다.
다음 그림을 주목하자.
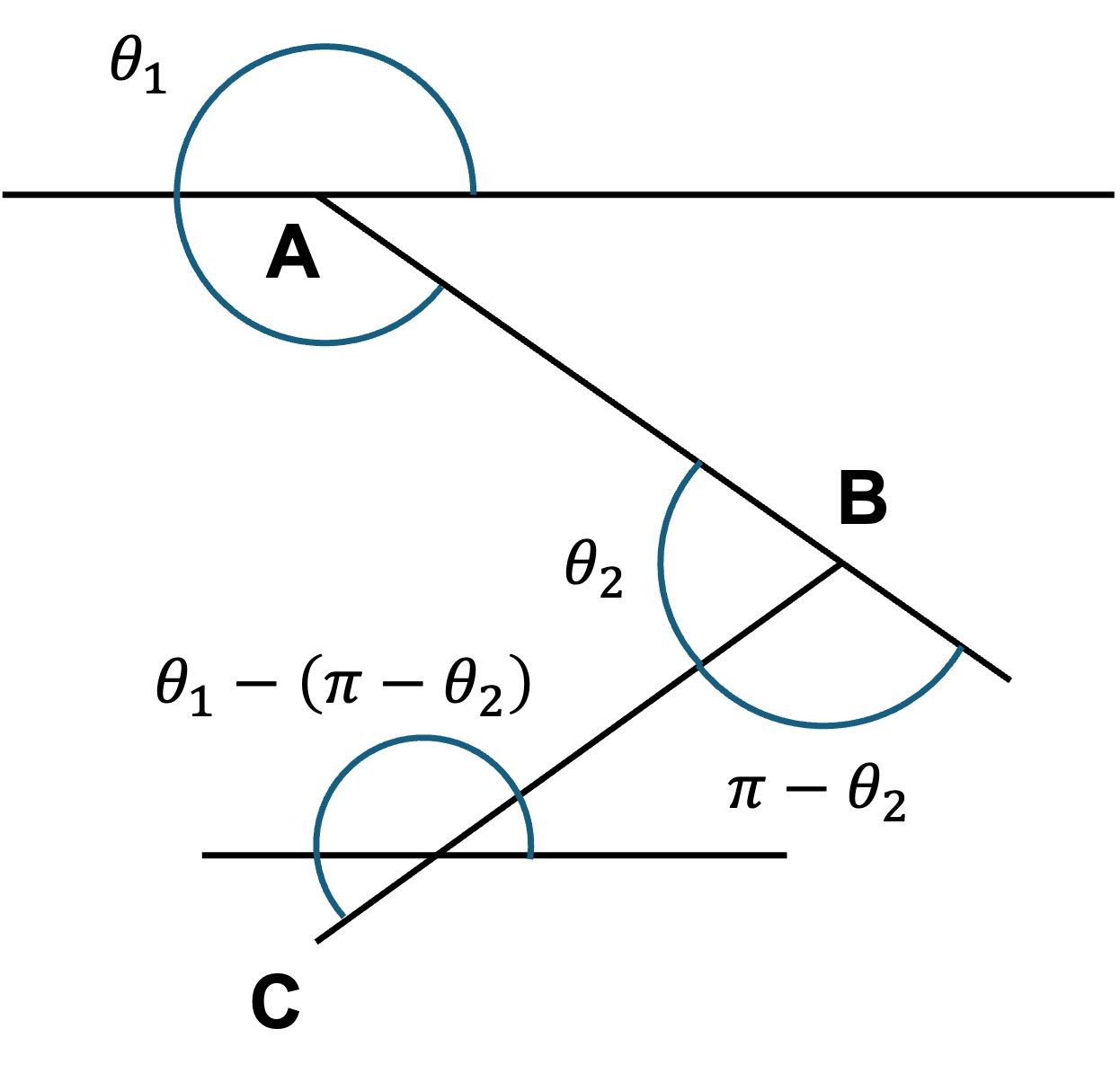
그 일정한 각도를 θ2라고 할 때, θ1 - 5(π - θ2) ≡ θ1 mod 2π ⇔ 5θ2 ≡ π mod 2π ⇔ θ2 = π/5, 3π/5임을 알 수 있다.
θ2 = 3π / 5라면 정오각형이 된다. △ABE에서 제2코사인 법칙을 적용하면 12 + 12 - 2 cos (3π/5) = |k|2을 얻고, △BCE에서 제2코사인 법칙을 적용하면 12 + |k|2 - 2k cos (2π/5) = |k|2을 얻는다. cos (3π/5) + cos (2π/5) = 0이므로, 연립하면 |k|3 - 2|k| - 1 = (|k|+1)(|k|2 - |k| - 1) = 0을 얻는다. 그러므로 |k| = (1 + √5) / 2를 얻는다. 벡터의 방향성을 고려하면 k = (-1 - √5) / 2를 얻을 수 있다.
θ2 = π/5라면 별모양이 된다. 군이론에 의해 k = (-1 - √5) / 2와 무리수 대칭을 이루는 값 k = (-1 + √5) / 2를 얻는다.
4. 양의 정수 n과 양수 aij (1 ≤ i, j ≤ n)에 대하여 An, Bn, Cn을 다음과 같이 정의하자.

다음 부등식을 증명하여라.
An ≤ nBn ≤ n2Cn
Solution.
이해를 위해 n2Cn = (12 + ··· + 12)Cn ≥ An은 코시-슈바르츠 부등식으로 빠르게 증명할 수 있음을 먼저 확인한다.
Bn2 ≤ n2Cn2은 다음과 같이 증명할 수 있다.

또한, An ≤ nBn은 다음과 같이 증명할 수 있다.

참고로, 재배열 부등식은 변수들이 대칭성을 가질 때 성립하는 부등식이다. 예를 들어, α2 + β2 + γ2 ≥ αβ + βγ + γα와 같이 큰 값끼리 묶을수록 전체 값이 더 커지는 경향을 보이는 경우가 대표적이다.
5. 양의 정수 n과 실수 α = π / (n + 1)에 대하여 크기가 n × n인 행렬 A를 다음과 같이 정의하자.
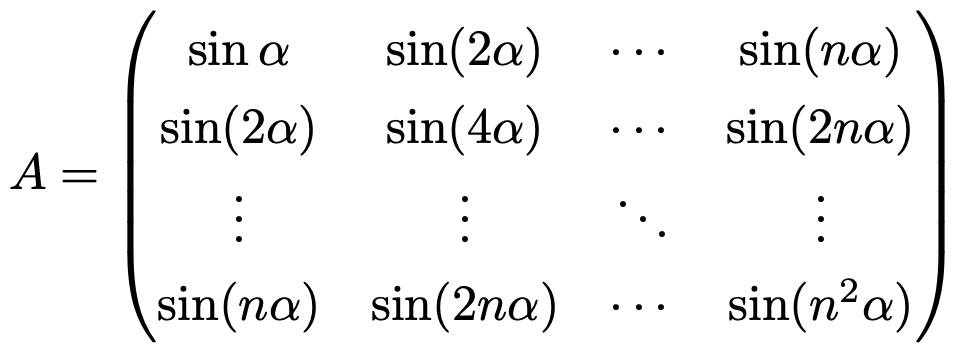
행렬식 det A의 절댓값을 구하여라.
Solution.
아래와 같은 40회 대수경 2분야 3번과 유사하긴 하지만 αi - βj = π/2 - i × j × π / (n + 1)인 αi, βj는 존재하지 않으므로 다른 문제이다.
참고로, 선형대수학은 1차식을 다루기 때문에 i × j 같은 2차 항이 나올 여지가 없어서 A 행렬을 두 개의 행렬의 곱으로 분해하는 게 불가능하다.
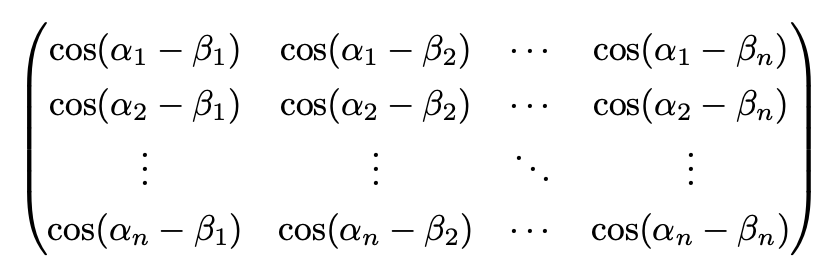
한편, 아래와 같은 코사인 수열합에 관한 공식(cf. 36회 대수경 1분야 7번)을 확인하자.
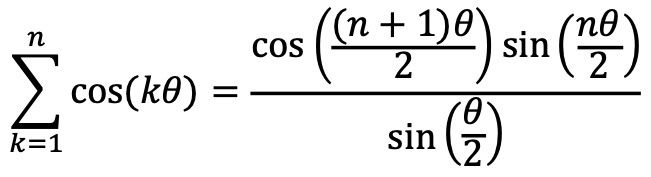
따라서 AᵀA는 다음과 같다.
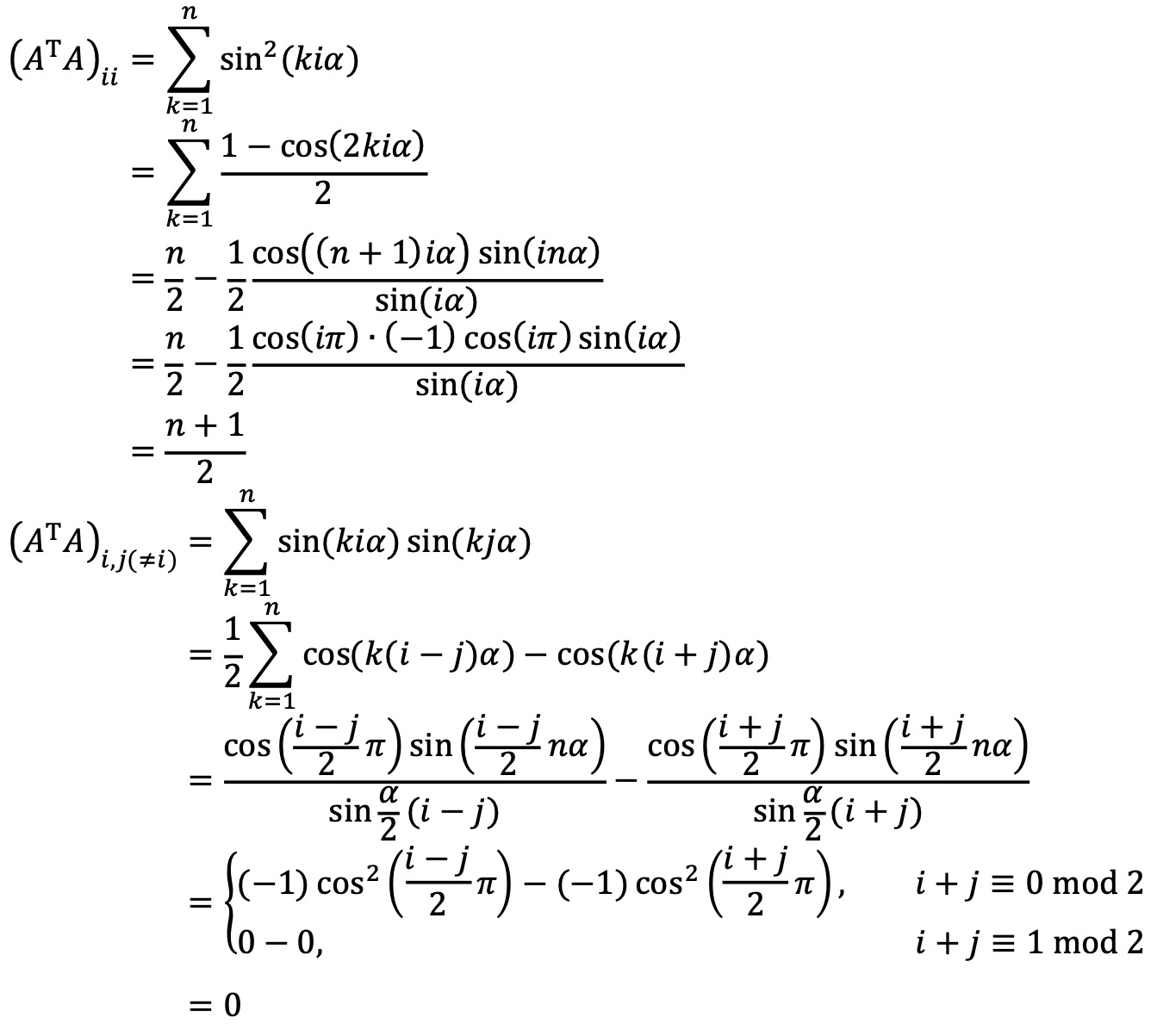
따라서 A의 행렬식은 다음과 같다.
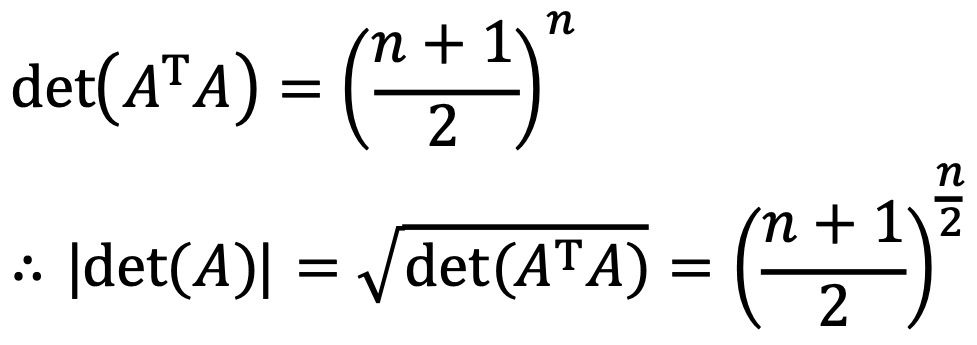
위와 같은 풀이는 Gram 행렬의 행렬식을 구하는 과정에서 착안한 것이다.
참고로, A의 x행 y열 원소를 Im(exp(ixyα))로 표현하고, Vandermonde 행렬처럼 표현했으나 Im 때문에 행렬식을 구할 수 없었다.
6. 크기가 (n+1) × (n+1)인 실행렬 A = (ajk)와 n 변수 다항식을 성분으로 가지는 크기가 n × n인 행렬 B = (bjk)를 다음과 같이 정의하자.

다음을 증명하여라.
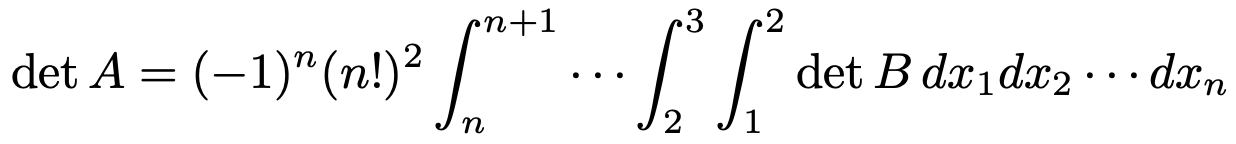
Solution.
n = 3인 경우 B와 det B는 다음과 같이 나타낼 수 있다.
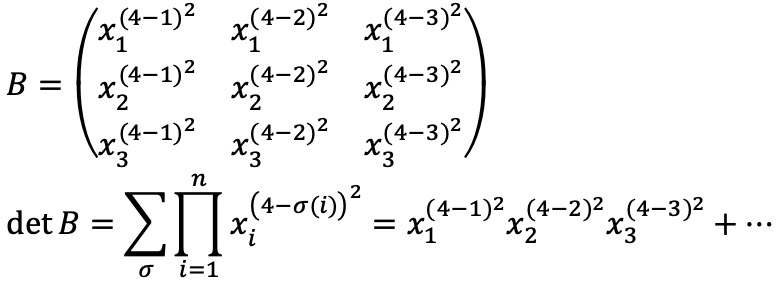
치환 개념을 적절히 쓰면 ∫ ⋯ ∫ det B dx1 ⋯ dxn = det ( (∫ bjk dxj)1≤j,k≤n )임을 보일 수 있어, 행렬식의 성질과 함께 (준식)을 보일 수 있다.

중간에 이해를 돕기 위해 n = 3인 경우로 한정하여 기술하였으나, 일반성을 잃지 않고 모든 n에 대해 성립함을 쉽게 알 수 있다.
7. 양의 정수 n, k ≥ 2에 대하여 함수 F : (0, 1)n → ℝ를 다음과 같이 정의하자.
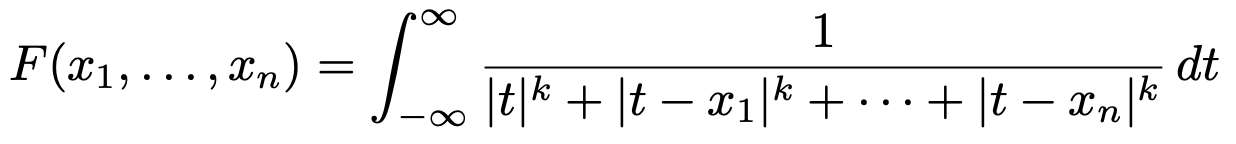
다음 적분이 수렴하는 양수 p의 범위를 구하여라.
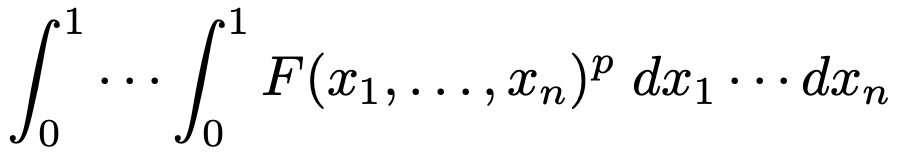
Solution.
F는 스케일링 성질을 가진다. 즉, F(λx) = λ1-kF(x)이다.

x가 원점에서 멀리 떨어진 부분은 F(x)가 발산하지 않고 어떤 유한한 상수로 잘 유계가 된다.
따라서 그 부분에서 F(x)p의 적분은 항상 수렴한다.
한편, x = rθ로 두면 F(x) = F(rθ) = r1-kF(θ)이고 F(θ)는 연속함수이므로, C1r1-k ≤ F(x) ≤ C2r1-k를 얻는다.
따라서 x가 원점에서 가까운 부분(|x| < ε ≪ 1)은 F(x)p ~ rp(1-k)가 된다.
그러므로 (준식) = ∫(0,1)n F(x)p dx ~ ∫(0,2π) ∫(0,ε) rn-1 · rp(1-k) dr dθ < ∞ ⇔ (n-1) + p(1-k) + 1 > 0 ⇔ p < n / (k-1)을 얻는다.
이때, F(x)가 x = 0 근처에서 발산하므로 ∫(0,1)n F(x)p dx ~ ∫(0,ε)n F(x)p dx가 성립함을 이용하였다.
입력: 2025.12.05 20:25
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 43회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2025.12.08 |
|---|---|
| 【대수경】 제 26회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.10.18 |
| 【대수경】 제 26회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2025.10.13 |
| 【대수경】 제 34회 전국 대학생 수학 경시대회 제 1 분야 (4) | 2025.06.15 |
| 【대수경】 제 35회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2025.04.20 |




최근댓글