8강. 순차논리(sequential logic)
추천글 : 【논리설계】 논리설계 목차
1. 개요 [본문]
2. 유한상태기계 [본문]
3. 여기표와 state encoding [본문]
4. state minimization [본문]
5. 순차논리회로의 종류 [본문]
6. 시스템의 설계 [본문]
1. 개요 [목차]
⑴ 조합논리회로(combinational logic circuit)
① 값을 저장하지 못함
② 클럭을 사용하지 않음
③ 입력의 변화가 출력에 바로 반영됨
④ 예 : adder, multiplexer, decoder, encoder, gate
⑵ 순차논리회로(sequential logic circuit) : 조합논리회로와 메모리 소자의 조합
① 값을 저장하는 래치, 플립플롭, 레지스터, 메모리 등의 소자가 있어서 상태를 저장함
② 대부분 클럭을 사용하여 값을 저장 (예외 : 래치)
③ 예 : clock divider, counter, register, FSM
2. 유한상태기계 [목차]
⑴ 유한상태기계(FSM, finite state machine) : state 간 상호작용 및 I/O를 맵핑하여 순차논리회로를 간략히 구현한 것
① 비슷하게 ASM(algorithmic state machine)도 있다.
⑵ Mealy machine
Figure 1. Mealy machine의 한 예시
① edge 상에 표시된 "L/R"에서 왼쪽은 입력값, 오른쪽은 출력값이다.
② 출력이 현재 state와 현재 입력의 함수로 표현된다.
③ 문제 1. 입력이 asynchronous하면 출력도 asynchronous하다. (& vice versa)
○ 이로 인해 Mealy machine은 glitch가 발생할 수 있다.
④ 문제 2. clock이 너무 느리면 입력을 주어도 state가 바뀌지 않을 수 있다.
⑤ 문제 3. clock이 너무 빠르면 입력을 여러 차례 준 것으로 인식될 수 있다.
⑥ 상기의 이유로 실제 시스템 설계 시 전혀 쓰지 않는 모델이다.
⑶ Moore machine
Figure 2. Moore machine의 한 예시
① 출력이 현재 state의 함수로 표현된다; 따라서 synchronous하다.
② 출력을 state로 표현하는 과정이 추가돼 Mealy machine보다 어려운 편이다.
3. 여기표 및 state encoding [목차]
⑴ 여기표(excitation table, state transition table)
① 정의 : 순차논리회로에서 진리표를 여기표라고 지칭
② current state와 input에 대한 함수로 next state 및 output을 표현함
③ 여기표를 통해 조합논리회로 이론을 활용할 수 있음 (ref)
④ self-starting: 모든 don't-care를 활용하여 모든 무효 케이스가 유효해진 것
○ 어떤 상태로 초기화돼도 정상 작동할 것임을 확신할 수 있음
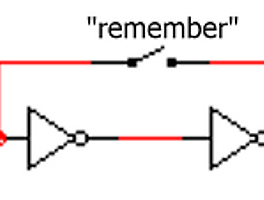
Figure 3. self-starting 회로의 예시
⑵ state encoding
① 정의 : state, input, output의 이름들을 이진수로 나타내는 것
② state encoding과 bit 수
○ 더 적은 비트수의 state encoding은 적은 F/F를 필요로 하지만 복잡할 수 있음
○ 더 많은 비트수의 state encoding(e.g., one-hot)은 많은 F/F를 필요로 할 수 있음
○ one-hot encoding : n개의 state를 표현시 단 한 bit만 1인 n 비트 수로 표현하는 방법
○ 회로 구성 시 용이함
④ heuristic encoding
○ highest priority : 입력이 같으면 다음 state가 같은 state의 집합
○ medium priority : 한 state의 다음 states
○ lowest priority : 입력이 같으면 출력이 같은 state의 집합
⑶ shift register로 clock 주기 단위의 어떤 신호도 생성할 수 있다.
Figure 4. shift register로 생성된 단위 시간 간격의 신호
4. state minimization [목차]
⑴ equilibrium state
① 서로 동등하게 취급할 수 있는 서로 다른 state를 지칭한다.
② Mealy machine : next state, next output 패턴이 같아야 한다.
③ Moore machine : next state, current output 패턴이 같아야 한다.
| Current State |
Next State |
Output |
|
| X = 0 |
X = 1 |
||
| A |
D |
C |
0 |
| B |
F |
H |
0 |
| C |
E |
D |
1 |
| D |
A |
E |
0 |
| E |
C |
A |
1 |
| F |
F |
B |
1 |
| G |
B |
H |
0 |
| H |
C |
G |
1 |
Table 1. excitation table의 예시
⑵ row matching method
① 새 연산 도입 : (A B) = (A)(B)
○ A, B는 부분집합을 가리키는 기호이다.
○ ∀a ∈ A, ∀b ∈ B, a ≢ b
② 1st. (A B C D E F G H) = (A B D G)(C E F H) (Output 기준)
| Current State |
Next State |
Output |
|
| X = 0 |
X = 1 |
||
| A |
A |
C |
0 |
| A |
C |
C |
0 |
| C |
C |
A |
1 |
| A |
A |
C |
0 |
| C |
C |
A |
1 |
| C |
C |
A |
1 |
| A |
A |
C |
0 |
| C |
C |
A |
1 |
Table 2. row matching method 과정 (1)
③ 2nd. (A B D G)(C E F H) = (A D G)(B)(C E F H)
| Current State |
Next State |
Output |
|
| X = 0 |
X = 1 |
||
| A |
A |
C |
0 |
| B |
C |
C |
0 |
| C |
C |
A |
1 |
| A |
A |
C |
0 |
| C |
C |
A |
1 |
| C |
C |
B |
1 |
| A |
B |
C |
0 |
| C |
C |
A |
1 |
Table 3. row matching method 과정 (2)
④ 3rd. (A D G)(B)(C E F H) = (A D)(G)(B)(C E H)(F)
| Current State |
Next State |
Output |
|
| X = 0 |
X = 1 |
||
| A |
A |
C |
0 |
| B |
F |
C |
0 |
| C |
C |
A |
1 |
| A |
A |
C |
0 |
| C |
C |
A |
1 |
| F |
F |
B |
1 |
| G |
B |
C |
0 |
| C |
C |
G |
1 |
Table 4. row matching method 과정 (3)
⑤ 4th. (A D)(G)(B)(C E H)(F) = (A D)(G)(B)(C E)(H)(F)
| Current State |
Next State |
Output |
|
| X = 0 |
X = 1 |
||
| A |
A |
C |
0 |
| B |
F |
H |
0 |
| C |
C |
A |
1 |
| A |
A |
C |
0 |
| C |
C |
A |
1 |
| F |
F |
B |
1 |
| G |
B |
H |
0 |
| H |
C |
G |
1 |
Table 5. row matching method 과정 (4)
⑥ 5th. 더이상 나뉘지 않으므로 A ≡ D, C ≡ E라고 결론지을 수 있다.
⑦ 자명하게 다항식 시간이 소요됨을 알 수 있다.
⑶ implication chart method
① 1st. 다음과 같이 excitation table의 내용을 옮긴다.
| B |
DC / FH |
|
|
|
|
|
|
| C |
DC / ED |
FH / ED |
|
|
|
|
|
| D |
DC / AE |
FH / AE |
ED / AE |
|
|
|
|
| E |
DC / CA |
FH / CA |
ED / CA |
AE / CA |
|
|
|
| F |
DC / FB |
FH / FB |
ED / FB |
AE / FB |
CA / FB |
|
|
| G |
DC / BH |
FH / BH |
ED / BH |
AE / BH |
CA / BH |
FB / BH |
|
| H |
DC / CG |
FH / CG |
ED / CG |
AE / CG |
CA / CG |
FB / CG |
BH / CG |
| |
A |
B |
C |
D |
E |
F |
G |
Table 6. implication chart method 과정 (1)
② 2nd. 우선 output에 따라 equilibrium state가 아닌 것들을 지운다.
| B |
|
|
|
|
|
|
|
| C |
|
|
|
|
|
|
|
| D |
|
|
|
|
|
|
|
| E |
|
|
|
|
|
|
|
| F |
|
|
|
|
|
|
|
| G |
|
|
|
|
|
|
|
| H |
|
|
|
|
|
|
|
| |
A |
B |
C |
D |
E |
F |
G |
Table 7. implication chart method 과정 (2)
③ 3rd. 1회 반복(상 → 하, 좌 → 우)
| B |
|
|
|
|
|
|
|
| C |
|
|
|
|
|
|
|
| D |
|
|
|
|
|
|
|
| E |
|
|
|
|
|
|
|
| F |
|
|
|
|
|
|
|
| G |
|
|
|
|
|
|
|
| H |
|
|
|
|
|
|
|
| |
A |
B |
C |
D |
E |
F |
G |
Table 8. implication chart method 과정 (3)
④ 4th. 2회 반복(상 → 하, 좌 → 우)
| B |
|
|
|
|
|
|
|
| C |
|
|
|
|
|
|
|
| D |
|
|
|
|
|
|
|
| E |
|
|
|
|
|
|
|
| F |
|
|
|
|
|
|
|
| G |
|
|
|
|
|
|
|
| H |
|
|
|
|
|
|
|
| |
A |
B |
C |
D |
E |
F |
G |
Table 9. implication chart method 과정 (4)
⑤ 5th. 더 이상 지울 수 없는 경우 체크되지 않은 칸이 바로 equilibrium state 쌍이다.
○ 순환 논리적인 항들이 남아 있을 수도 있다.
⑥ 자명하게 다항식 시간이 소요됨을 알 수 있다.
⑷ 만약 FSM이 don't-care를 가지고 있는 경우 두 방법은 사용할 수 없다.
① 아래 예시에서 "S0 = S1, S1 = S2이므로 S0 = S2"인가?
Table 10. don't-care 조건을 포함하는 FSM의 예시
5. 순차논리회로의 종류 [목차]
⑴ 인터록(interlock) 회로 : 한쪽이 동작하면 다른 한쪽은 동작할 수 없는 논리회로
⑵ 신입 신호 우선 회로 : 한쪽이 동작하면 다른 한쪽이 복구되는 논리회로
⑶ 동작 우선 회로 : 정해진 순서대로 동작되는 논리회로 (예: X1이 동작해야 X2가 동작할 수 있다.)
⑷ 시한 회로(on delay timer; Ton) : 입력을 주면 설정시간이 지난 후 출력이 동작(OFF → ON)
⑸ 시한 복구 회로(off delay timer; Toff) : 정지입력을 주면 설정시간이 지난 후 출력이 복구(ON → OFF)
⑹ 단안정 회로(monostable) : 입력을 주면 설정시간이 지난 후 빠르게 동작 및 복구(ON → OFF → ON)
① 시한 회로나 시한 복구 회로와 달리 NOT 게이트와 연결돼 기본 상태가 ON 상태
6. 시스템의 설계 [목차]
⑴ 시스템은 크게 2가지 부분으로 나뉜다.
⑵ data unit : 데이터를 저장, 결합 또는 처리하는 부분
⑶ control unit : 프로세스를 시작, 중단, 검토, 통신 및 결정하는 부분
입력: 2016.11.20 21:40
'▶ 자연과학 > ▷ 논리설계' 카테고리의 다른 글
| 【논리설계】 응용 : 덧셈기 (0) | 2016.11.27 |
|---|---|
| 【논리설계】 9강. 프로토콜 (0) | 2016.11.22 |
| 【논리설계】 7강. 클럭과 메모리 (0) | 2016.10.26 |
| 【Logic Design】 adder circuits (0) | 2016.10.10 |
| 【논리설계】 6강. Implementation Technology (3) | 2016.09.28 |
최근댓글