12강. 직류회로이론 (time-domain)
추천글 : 【회로이론】 회로이론 목차
1. 직렬-병렬 합성(series-parallel simplification) [목차]
⑴ 전원의 직렬-병렬 합성
① 전압원의 직렬연결로 인한 합성 전압은 각 전압원의 전압의 총합과 같움
② 서로 다른 전압을 내는 전압원의 병렬연결 시 폭발할 수 있음
③ 서로 같은 전압 v를 내는 전압원의 병렬연결 시 합성 전압은 v임 (수명 ↑)
④ 서로 다른 전류를 내는 전류원의 직렬연결 시 폭발할 수 있음
⑤ 서로 같은 전류 i를 내는 전류원의 직렬연결 시 합성 전류는 i임 (수명 ↑)
⑥ 전류원의 병렬연결로 인한 합성 전류는 각 전류원의 전류의 총합과 같음
⑵ 부하의 직렬-병렬 합성 : 여러 소자들을 하나의 소자로 취급할 수 있음
① 저항의 직렬연결
Figure. 1. 저항의 직렬연결

② 저항의 병렬연결
Figure. 2. 저항의 병렬연결
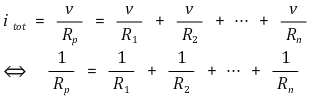
③ 커패시터의 직렬-병렬 합성
④ 코일의 직렬-병렬 합성
⑤ 응용 : 각 소자의 전력의 합과 합성 소자의 전력과 같음
○ 모든 전력은 전원에서 공급
○ 전원을 흐르는 전류는 소자 각각으로 계산한 것과 합성 소자로 계산한 것이 같음
⑶ 밀만의 정리(Milman's theorem)
① 두 개의 저항이 있는 경우
② R1, ···, Rn에 대하여 유사한 형태로 확장할 수 있음
2. 키르히호프 법칙(Kirchhoff's law) [목차]
⑴ 키르히호프 전류법칙(KCL, Kirchhoff current law) : 전하의 연속방정식. node 중심 해석
Figure. 4. 키르히호프 전류법칙
① 키르히호프 법칙은 선형 / 비선형, 집중정수계 / 분포정수계, 시변 / 시불변에 관계없이 적용 가능
② 흘러 나가든 흘러 들어가든 반드시 한 가지로 통일 : 음의 값도 고려
○ 전자기학 관점 : 열 물리처럼 계에서 나가는 경우를 양의 값으로 함. 임의의 node에서 나가는 전류의 합은 0임
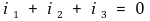
○ 전자공학 관점 : 열 화학처럼 계로 들어가는 경우를 양의 값으로 함. 임의의 node로 들어오는 전류의 합은 0임
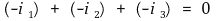
③ node voltage analysis이라고도 함 : 각 node의 전압을 정의한 뒤 KCL을 이용하기 때문
④ 슈퍼노드(super-node) : 전원과 연결돼 있는 두 개 이상의 node로 구성. 미지수를 줄일 수 있음
Figure. 5. 슈퍼노드

⑤ 팁. mesh current analysis보다 node voltage analysis를 추천
⑥ 예제 1.
Figure. 6. 예제 1

⑦ 예제 2.
Figure. 7. 예제 2
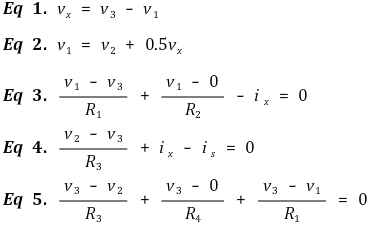
⑵ 키르히호프 전압법칙(KVL, Kirchhoff voltage law) : 메시 또는 루프 중심 해석
① 경로(path)의 유형
○ 메시(mesh) : 가장 기본이 되는 회로
○ 루프(loop) : 단선된 부분이 없이 이어진 회로. 폐곡선, 폐루프라고도 함
○ 예시
○ ⒜ : 이것은 path가 아님. KVL이 성립하지 않음
○ ⒝ : 이것은 path가 아님. 같은 node를 두 번 지나기 때문
○ ⒞ : 이것은 다른 loop를 내부에 포함한다는 점에서 mesh가 아님
○ ⒟ : ⒞와 같은 이유로 이것은 mesh가 아닌 loop임
○ ⒠, ⒡ : 이것은 loop이면서 mesh임
○ 굳이 mesh를 잡을 필요는 없음 : 하지만 일차독립인 연립방정식을 만들려면 mesh로 하는 게 전략적
② 임의의 폐곡선의 전압강하(voltage drop)의 합은 0임
Figure. 9. 키르히호프 전압법칙
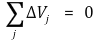
③ mesh current analysis이라고도 함 : 각 mesh를 정의한 뒤 KVL을 적용하기 때문
○ mesh마다 mesh current를 지정
○ 각 소자에 흐르는 전류는 mesh current의 합 또는 차로 표현
○ mesh 위에서 KVL을 적용한다.
○ 팁. mesh current를 지정하지 않고, 미지의 지점을 변수로 지정할 수도 있음
④ 증명 1.
○ 기본적으로 전기장 E는 보존장 : 임의의 폐곡선을 X(t), a ≤ t ≤ b로 매개화할 수 있음 (단, X(a) = X(b))
○ 수식 전개 : grad V = E에 대해
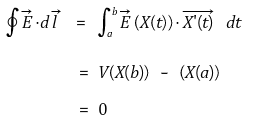
○ (참고) 이 증명은 보존장에 대한 에너지 보존 법칙을 유도할 때 동일하게 쓰임
○ (참고) E와 dl의 내적은 전압강하를 의미
○ (참고) 에너지 보존 법칙과 전압강하 해석을 결합 : 전위의 감소만큼 단위전하에게 일이 가해짐
⑤ 증명 2.
○ 맥스웰 3법칙 : Faraday 법칙. 외부 자기장의 변화는 전계를 유도
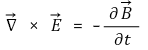
○ 외부 자기장의 변화가 없는 경우 curl E 벡터 = 0 : Green 정리 이용

⑥ 한계 : KCL로밖에 풀 수 없는 문제가 있음 (예 : Op Amp)
⑦ 예제 1.
Figure. 10. 예제 1
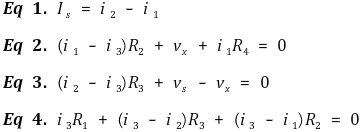
⑶ 모든 회로는 KCL과 KVL로 풀 수 있음
① 따라서 임의의 지점의 전압과 전류를 알 수 있음
② (주석) 등가회로의 존재성과 귀납법을 통해 증명할 수 있을 듯
3. 중첩의 원리(superposition principle) [목차]
⑴ 정의 : 회로 내 독립전원이 둘 이상인 경우 각각의 독립전원으로 인한 제어량을 합한 것은 실제 제어량과 같음
① 선형소자 : 중첩의 원리가 적용되는 소자. 저항(R), 커패시터(C), 인덕터(L), 선형 전원 등
② 전기장이 선형성이 있으므로 중첩의 원리가 성립
③ 전력은 적용되지 않음
④ 소신호 해석(small-signal analysis)에서도 중첩의 원리를 적용할 수 있음
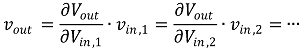
⑵ 평균전력의 중첩의 원리 : 주기를 가지는 전원에 대하여
① 교류 전원의 전력은 평균전력을 의미
Figure. 11. 평균전력의 중첩의 원리
② 대부분 평균전력의 중첩의 원리가 적용되지 않음
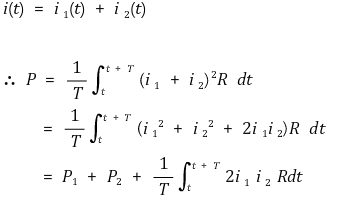
③ 주파수가 모두 다른 교류전원으로만 구성된 경우 평균전력 중첩의 원리가 적용 가능
⑶ 예제
Figure. 12. 중첩의 원리 예제
① 전원의 제거
Figure. 13. 전원의 제거
② 1st. 독립 전류원 제거 : 전류를 0으로 함 ⇔ 개방회로(open)
Figure. 14. 독립 전류원 제거
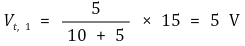
③ 2nd. 독립 전압원 제거 : 전압을 0으로 함 ⇔ 단락회로(short)
Figure. 15. 독립 전압원 제거
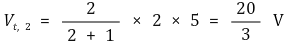
④ 3rd. 부하 전압은 두 독립전원에 대해 선형적
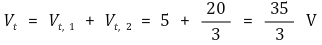
4. 등가회로 : 부하효과가 동일한 회로 [목차]
⑴ 부하효과(loading effect) : 개방전압과 부하전압이 달라지는 현상
① 개방전압
Figure. 16. 개방전압
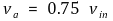
② 부하전압
Figure. 17. 부하전압

⑵ 테브낭 등가회로(Thevenin equivalent circuit)
① 표현
Figure. 18. 테브낭 등가회로 표현
○ Rth가 음수이면 종속 전원이 존재한다는 의미
○ 독립 전원만 존재한다면 테브낭 등가저항 Rth는 항상 양수
② 실험상 방법
Figure. 19. 실험상 방법
○ Itest - Vtest 그래프를 통해 Vth와 Rth를 계산
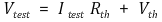
○ 개방전압 측정 : 내부저항이 각각 R1, R2인 전압계로 측정한 개방전압이 V1, V2라고 정의
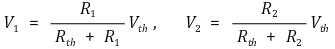
③ 테브낭 등가회로 예제
Figure. 20. 테브낭 등가회로 예제
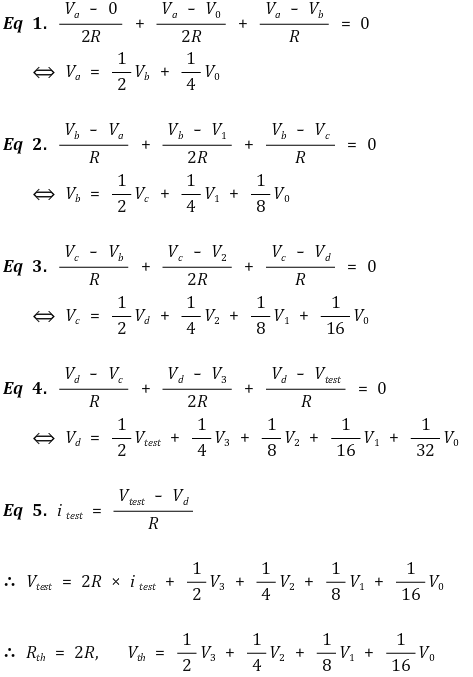
⑶ 노튼 등가회로(norton equivalent circuit) : Thevenin 등과회로와 쌍대를 이룸
① 표현
Figure. 21. 노튼 등가회로 표현
⑷ 테브낭 - 노튼 가역성(source transformation)
① 수식화
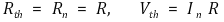
② 테브낭 - 노튼 가역성 : 저항
Figure. 22. 저항의 테브낭 - 노튼 가역성
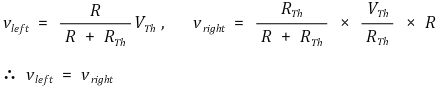
③ 테브낭 - 노튼 가역성 : 커패시터
④ 테브낭 - 노튼 가역성 : 코일
⑤ 테브낭 - 노튼 가역성 증명
Figure. 23. 테브낭 - 노튼 가역성 증명
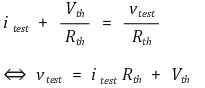
⑸ Lemma 1. 다음과 같은 회로는 항상 등가화가 가능 (존재성)
① 모든 회로가 등가화 가능한 것은 아님
○ 부하 부분에는 어떤 소자가 와도 상관없음
② case 1. 등가화가 적용되는 영역이 모두 저항과 전원으로 이루어진 회로
○ 전략 : 회로 내 특정 소자를 기준으로 그것과 가까운 소자부터 테브낭 등가회로를 그려 나감
○ 중간에 저항을 만났을 경우 : 테브낭 - 노튼 가역성(source transformation)을 이용
○ 중간에 전압원을 만났을 경우 : vtest = itestRth + vth에서 vth에 변화를 줌
○ 중간에 전류원을 만났을 경우: 노튼 등가회로로 바꾼 뒤 KCL을 적용
○ 독립전원만 있는 회로에서는 결코 Rth가 음수일 수 없음
③ case 2. 모든 전원이 동일한 주파수를 갖는 교류회로일 경우: R, L, C를 저항처럼 간주할 수 있기 때문
⑹ Lemma 2. 모든 회로는 유일한 Thevenin 등가회로를 가짐 (유일성)
① 한 회로가 A와 B라는 Thevenin 등가회로를 가진다고 가정
② 이때 회로 내 두 단자의 개방전압(open voltage)가 같아야 함 ⇒ A와 B의 Vth는 서로 같음
③ 회로 내 두 단자의 단락전류(short current)가 같아야 함 ⇒ A와 B의 Vth ÷ ith = Rth가 서로 같음
④ 결론 : A와 B는 동일
⑺ Lemma 3. 임의의 회로와 그것의 등가회로의 소모 전력은 서로 다를 수 있음
Figure. 25. 등가회로의 소모전력이 같지 않음을 보여주는 예
① ⒜의 경우 : N 내부에서 저항에서의 소모 전력은 10 W
② ⒝의 경우 : Nth 내부에서 저항에서의 소모 전력은 1 W
③ 두 단자에 대해 ⒜와 ⒝가 부하효과가 같기 때문에 부하전력은 항상 같음
⑻ 한 시스템이 부하저항에 가할 수 있는 최대전력
① 신호 분야의 조건
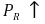
② 전력 분야의 조건
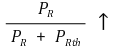
③ 신호 분야에서 저항 R이 갖춰야 하는 조건
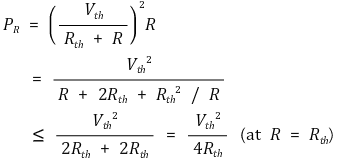
5. 과도현상(transient phenomenon) [목차]
⑴ 정의 : R, L, C 소자 해석에 있어 미분방정식을 활용하는 것
⑵ 일반해(general solution), 완전해(complete solution) = 재차해 + 특해
⑶ 제차해(homogeneous solution), 과도해(transient solution)
① 정의 : 미분방정식의 계수에 의해 결정되는 해
⑷ 특수해(particular solution), 정상상태 해(steady state solution, static state solution)
① 정의 : 구동항의 형태에 의해 결정되는 해
② 구동항 : 일반적으로 좌변은 선형 미분방정식, 우변은 특정 함수로 둠. 그 특정 함수를 지칭
입력: 2016.01.05 19:49
수정: 2018.12.11 23:52
'▶ 자연과학 > ▷ 회로이론' 카테고리의 다른 글
| 【회로이론】 회로이론 응용 : Logic Probe (0) | 2016.06.27 |
|---|---|
| 【회로이론】 13강. 휘트스톤(휘스스톤) 브릿지와 센서 (0) | 2016.06.27 |
| 【회로이론】 5강. 스위치, 퓨즈, 접지, d'Arsonval meter (0) | 2016.06.27 |
| 【회로이론】 3강. 저항 (0) | 2016.06.27 |
| 【회로이론】 2강. 전원 (0) | 2016.06.27 |





























최근댓글