2강. 집합의 크기
추천글 : 【해석학】 해석학 목차
1. 자연수, 정수, 유리수의 정의 [본문]
2. 셀만하다는 것 [본문]
1. 자연수, 정수, 유리수의 정의 [목차]
⑴ 귀납성의 정의 : 집합 I ⊆ ℝ가 귀납적이라는 것은 다음을 의미
① 요건 1. 1 ∈ I
② 요건 2. x ∈ I일 때마다 x + 1 ∈ I
⑵ 자연수, 정수, 유리수의 정의
① 자연수의 집합 ℕ은 다음과 같이 정의
ℕ = {x ∈ ℝ | I가 귀납적일 때마다 x ∈ I임}
② 1 + 1을 2, 2 + 1을 3과 같이 씀
③ 정수의 집합 ℤ는 다음과 같이 정의
ℤ = ℕ ∪{0}∪{-n | n ∈ ℕ}
④ 유리수의 집합 ℚ는 다음과 같이 정의
ℚ ={m / n | m ∈ ℤ, n ∈ ℕ}
⑶ 예제 : I ⊆ ℝ가 귀납적이면 ℕ ⊆ I임을 보이시오.
○ 풀이
각 n ∈ ℕ에 대해 n ∈ I이다.
따라서 ℕ ⊆ I이다.
⑷ 예제 : ø ≠ A ⊆ ℕ이면 min A가 존재함을 보이시오.
○ 풀이
ø ≠ A ⊆ ℕ이면 min A가 존재하는 것과 A ⊆ 이 min A를 갖지 않으려면 A = ø인 것과 동치이다. (대우 명제)
모든 n ∈ ℕ에 대해 {k ∈ ℕ | 1 ≤ k ≤ n}∩ A = ø임을 증명하면 족하다.
이는 다시 I ={n ∈ ℕ |{k ∈ ℕ | 1 ≤ k ≤ n}∩ A = ø}가 귀납적임을 증명하면 족하다.
1 ∈ A인 경우 1 = min A이므로 1 ∉ A이다. 따라서 1 ∈ I이다.이제 n ∈ I라고 하면
{k ∈ ℕ | 1 ≤ k ≤ n}∩ A = ø이다.
만약 n+1 ∈ A이면 n+1 = min A이므로 n+1 ∉ A이어야 한다. 따라서 n+1 ∈ I이다.
따라서 I는 귀납적이고 준 명제를 증명하였다.
⑸ 예제 : ℕ은 위로 유계가 아님을 보이시오.
○ 풀이
만약 ℕ이 위로 유계라면 완비성 공리에 의해 v = sup ℕ이 존재한다.
모든 n ∈ ℕ에 대해 n+1 ∈ ℕ ≤ v이므로 n ≤ v - 1이다.
즉 ℕ ≤ v-1이고 예제 3 ②에 의해 v ≤ v-1이다.
따라서 1 ≤ 0이라는 모순이 나온다. ℕ은 위로 유계가 아니다.
2. 셀만하다는 것(what the countable is) [목차]
⑴ 집합 A가 셀만하다는 것은 전사함수 f : ℕ → A가 존재한다는 것
⑵ 예제 : 집합 ℤ, ℚ는 셀만함을 보이시오.
○ 풀이
lemma 1. ℤ는 셀만하다
proof 1. f : ℕ → ℤ를 f(1) = 0, f(2n) = n, f(2m+1) = -m이라 하면 f가 전사함수이다.
proof 1. 즉 0, 1, -1, 2, -2, 3, -3 ··· 순으로 자연수 집합 ℕ과 정수 집합 ℤ을 일대일 대응시킬 수 있다.
lemma 2. ℚ는 셀만하다
proof 2. g : ℕ → ℚ를 n ∈ ℕ에 대해 2n = 2a3b5c···로 소인수분해한 뒤 g(n) = (b-c) ÷ a라 하면 g가 전사함수임이 분명하다.
⑶ 예제 : 모든 a, b ∈ ℝ에 대해 a < b이면 a < q < b인 q ∈ ℚ가 존재함을 보이시오.
○ 풀이
경우 1. a, b ∈ ℝ이고 a < b라 하자. 먼저 a > 0인 경우를 다루자.
경우 1. n을 충분히 크게 잡으면 n > (1/a) + (1 / (b-a))가 되도록 할 수 있다.
경우 1. 또한 충분히 큰 m을 상기하면 A ={m ∈ℤ | a < m/n}인 A가 공집합이 아님을 알 수 있다.
경우 1. 이때 A ⊆{k ∈ ℕ | k > 1}임을 이해하고 넘어자자. (∵ a > 1/n)
경우 1. m = min A라고 하면 m-1 ∉ A이므로 a ≥ (m-1)/n이다. 즉, 다음이 성립한다.
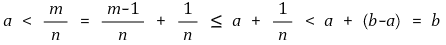
경우 1. m/n ∈ ℚ이므로 증명이 완료됐다.
경우 2. a, b ∈ ℝ이고 a ≤ 0이라 하자.
경우 2. n을 충분히 크게 잡으면 n > -a가 되도록 할 수 있다.
경우 2. 0 < n+a < n+b이므로 경우 1의 논리를 적용하면 n+a < q < n+b인 q ∈ ℚ가 존재한다.
경우 2. q - n ∈ ℚ이고 a < q-n < b이므로 증명이 완료됐다.
⑷ 예제 : 실수 집합 ℝ은 셀만하지 않음을 보이시오.
○ 풀이
자연수의 집합의 모든 원소를 실수구간 (0, 1]에 대응시키자.
ℕ에서 (0, 1]로의 전사함수 f가 존재한다고 가정하자.
전사함수 f가 다음과 같이 표현될 수 있다.
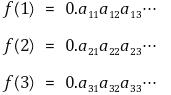
한편 어떤 (0, 1]의 한 원소 b를 다음과 같이 표현할 수 있을 것이다.

이때 bk가 f(k)의 소수점 아래 k번째 자리가 다르다고 할 때 b는 f와 대응되지 않는다.
모든 함수 f에 대해 위와 같은 b를 구성할 수 있다.
따라서 전사함수 f를 정의하는 것은 불가능하다.
즉, 실수 집합 ℝ은 셀만하지 않다.
⑸ 예제 : 모든 a, b ∈ ℝ에 대해 a < b이면 a < ℓ < b인 무리수 ℓ ∈ ℝ - ℚ가 존재함을 보이시오,
○ 풀이
ℚ는 셀만하고 ℝ는 셀만하지 않으므로 ℝ ≠ ℚ이다.
즉 c ∈ ℝ - ℚ가 존재한다.
c > 0인 경우를 생각하자. c < 0인 경우 -c를 고려하면 된다.
a < b이면 ac-1 < bc-1이고 예제 7 ②로부터 ac-1 <q < bc-1인 q ∈ ℚ가 존재한다.
a < qc < b인데 qc ∉ ℚ임이 분명하다.
왜냐하면 유리수 집합은 곱셈에 대해 닫혀있기 때문에 qc ∈ ℚ이면 c ∈ ℚ가 되기 때문이다.
⑹ 예제 : 집합 {G | G ⊆ ℕ}은 셀만한가?
○ 풀이
{G | G ⊆ ℕ}가 셀만하다는 것과 f : ℕ → {G | G ⊆ ℕ}가 존재하는 것과 동치이다.
H ={n ∈ ℕ | n ∉ f(n)}이라 하면 H ⊆ ℕ이고 f가 전사함수이므로 H = f(n)인 n이 존재한다.
이때 n ∈ H ⇔ n ∈ f(n)인데 n ∉ f(n)이므로 모순이다.
따라서 H는 공집합이고 f는 존재한다. 즉, 셀만하다.
⑺ 예제 : 각 자연수 n에 대해 집합 An이 셀만하면 합집합 Un∈ℕAn도 셀만함을 보이시오.
○ 풀이
각 n에 대해 전사함수 fn : ℕ → An이 존재한다.
이때 f : ℕ → UAn을 m ∈ ℕ에 대해 6m을 소인수분해하여 6m = 2n3k ···일 때
f(m) = fn(k)라 정의하면 분명히 f가 전사함수가 된다.
따라서 UAn은 셀만하다.
⑹ 예제 : 집합 ø ≠ A ⊆ ℝ이 각 자연수 n과 서로 다른 a1, ···, an ∈ A에 대해 | a1 + ··· + an | ≤ 1을 만족한다고 하자. 이때 A는 셀만하다는 것을 보이시오.
○ 풀이
b ∈ A를 고정하고 A1 = {b} ∪ (A ∩ {0})이라고 하자. 이때 An ={a ∈ A | |a| > 1/n}∪{b}는 셀만하다.
a ∈ A, a ∉ A1이라면 |a| > 0이므로 1 / |a| ∈ ℝ이다.
ℕ ≤ 1 / |a|이므로 n ∈ ℕ이 있어 |a| > 1/n ≥ 1/(n+1)이고 a ∈ An+1이다.
따라서 A = Un∈ℕAn이고 이제 각 An이 셀만함을 보이면 된다.
이를 위해 1 ≤ An의 원소의 개수 ≤ 1 + 2n임을 보이자.
만약 m ∈ ℕ, a1, ···, am > 0, a1, ···, am ∈ An이라면
m/n < a1 + ··· + am = |a1 + ··· + am| ≤ 1로부터 m < n임을 안다.
ai < 0일 때도 마찬가지이므로 증명이 완료되었다.
입력 : 2019.12.24 00:33
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 4강. 연속성 (3) | 2019.12.26 |
|---|---|
| 【해석학】 3강. 증가수열과 코시수열 (21) | 2019.12.25 |
| 【해석학】 1강. 실수의 공리와 함수 (0) | 2019.11.26 |
| 【수학】 2계 미분방정식 (0) | 2016.06.26 |
| 【해석학】 대수경 중 이상적분 문제 모음 (0) | 2016.06.25 |


최근댓글