3강. 증가수열과 코시수열
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 수렴의 수렴성과 기본 성질 [본문]
2. 코시수열 [본문]
1. 수열의 수렴성과 기본 성질 [목차]
⑴ 실수열 (an)n∈ℕ이 실수 a로 수렴한다는 것
① N ∈ ℕ, 모든 n > N에 대해
② 모든 양수 ε에 대해 궁극에는 | an - a | < ε인 N이 존재한다는 것
⑵ 수열 (an)과 증가하는 자연수열 n1 < n2 < ···가 있을 때 새로운 수열 (ank)k∈ℕ를 (an)의 한 부분수열이라고 함
⑶ 예제 : 다음을 증명하여라.
① 수열 (an)이 궁극에는 an = a이면 (an)은 a로 수렴한다.
② (an)이 a로 수렴하면 집합 {an}은 유계이다.
③ (an)이 a로 수렴하고 (bn)이 b로 수렴한다고 하자. 궁극엔 an ≤ bn이면 a ≤ b임을 보이시오.
④ (an)이 a로 수렴하고 또 궁극엔 an ≤ b이면 a ≤ b이다.
⑤ (an)이 a로 수렴하고, (an)이 또한 b로 수렴하면 a = b이다. 즉, 수렴하는 수열의 수렴값은 유일하다.

⑷ 예제 : 다음을 증명하여라.
① (an)이 a로 수렴하면, 모든 부분수열 (an_k)도 a로 수렴한다.
② 수열 (1/n)은 0으로 수렴한다.
⑸ 예제 : 다음을 증명하여라.
① 0 < p < 1일 때 수열 (pn)은 0으로 수렴한다.
② an, a ∈ ℝ -{0}이고 a가 (an)의 수렴값이면
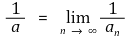
이 성립함을 보이시오.
⑹ 예제 : 다음을 증명하여라.
① 수열 (an) = (1, 0, 1, 0, ···)은 수렴하지 않는다.
② a가 (an)의 수렴값이고 b가 (bn)의 수렴값이면
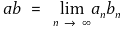
이 성립함을 보이시오.
⑺ 예제 : 다음을 증명하여라.
① 증가수열의 수렴성 : a1 ≤ a2 ≤ ···이고 (an)이 유계이면 (an)은 수렴함을 보이시오. 감소할 때도 같은 결론을 내릴 수 있는가?
② 두 수열 (an)과 (bn)을 a1 = 1, b1 = 2이고
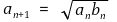
이며
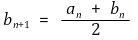
라고 하자. 이때 두 수열이 수렴함을 보이시오.
⑻ 예제 : 수열 (an)을 a1 = 3이고 각 n ∈ ℕ에 대해
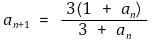
이라고 하자. (an)이 수렴함을 보이시오. 무엇으로 수렴하는가?
2. 코시수열(Cauchy sequence) [목차]
⑴ 코시수열의 정의
① N ∈ ℕ, 모든 n, m > N에 대해
② 실수열 (an)이 코시 수열이라는 것은 각 ε > 0에 대해 궁극에는 | an - am | < ε인 N이 존재한다는 것
⑵ ℝ2에서의 벡터열 ((an, bn))n∈ℕ이 벡터 (a, b)로 수렴한다는 것은

및
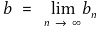
과 같다.
⑶ 무한급수 I를
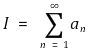
과 같이 정의하자. 실수열 (an)에 대해 무한급수 I가 A로 수렴한다는 것은 부분합의 수열 (An)이 A로 수렴한다는 것이다. 여기서 An = a1 + ··· + an이다.
⑷ Bolzano-Weierstrass 정리 : 실수열 (an)이 유계이면 수렴하는 부분수열을 갖는다. ((an, bn))n∈ℕ에 대해서도 같은 말을 할 수 있는가?
⑸ 예제 : (an)이 코시수열이면 수렴함을 보이시오.
⑹ 예제 :

이면
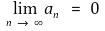
가 성립함을 증명하시오.
⑺ 예제 : (an)의 수렴값이 0이지만 무한급수 I가 존재하지 않는 예를 찾으시오.
⑻ 예제 : 실수 r에 대해 등비급수
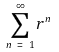
는 정확히 언제 수렴하는가?
⑼ 예제 : 실수열 a1, a2, a3, ···이 있어 각 n에 대해 an ≥ 0이라고 하자. 이때 무한급수

가 수렴할 필요충분조건은 부분합의 수열 (An)이 유계임을 보이시오.
⑽ 예제 : 무한급수
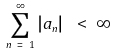
이 수렴하면 무한급수
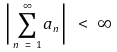
도 수렴함을 증명하시오.
⑾ 예제 : 수열 (an)을 a1 = 1이고 각 n ∈ ℕ에 대해

과 같이 정의하면 (an)이 수렴함을 보이시오. 무엇으로 수렴하는가? 이 극한을 무한연분수로 표현할 수 있는가?
○ 풀이
수학적 귀납법에 의해 a2n과 a2n-1은 증가수열임을 보일 수 있다.
또한 an < 2이므로 (an)은 위로 유계이다.
증가수열이고 유계인 수열은 수렴하므로 (a2n), (a2n-1)이 수렴한다.
다음 과정을 보면 알 수 있지만 (a2n)과 (a2n-1)의 수렴값은 동일하므로 (an)은 수렴한다.
(an)의 수렴값을 a라고 두면 다음과 같다.
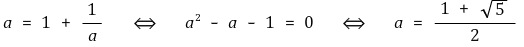
무한연분수 표현은 다음과 같다.
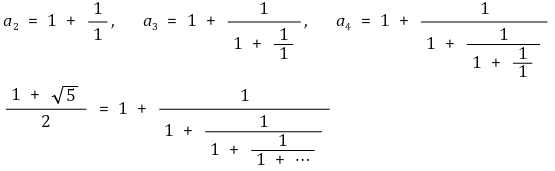
입력 : 2019.12.25 00:53
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 6강. 대수학의 기본정리 (0) | 2019.12.26 |
|---|---|
| 【해석학】 4강. 연속성 (3) | 2019.12.26 |
| 【해석학】 2강. 집합의 크기 (14) | 2019.12.24 |
| 【해석학】 1강. 실수의 공리와 함수 (0) | 2019.11.26 |
| 【수학】 2계 미분방정식 (0) | 2016.06.26 |



최근댓글