6강. 대수학의 기본정리
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 대수학의 기본정리 [본문]
1. 대수학의 기본정리 [목차]
⑴ 정리 : n ∈ ℕ, an, ···, a0 ∈ ℂ, an ≠ (0, 0)이면 복소수 z가 있어 p(z) = anzn + ··· a0 = 0임을 보이시오.
① 직관적 의미 : 임의의 다항식의 모든 해는 복소수 범위 안에 있음
② a0 = 0인 경우 자명한 해인 z = 0이 나오므로 a0 ≠ 0이라고 가정
③ 단계 1. 함수 φ : ℝ2 → ℝ이 φ(x, y) = |p(x, y)|일 때 φ가 연속함수이며 어떤 점 (x0, y0) = z0에서 최솟값을 가진다.
○ 풀이 : 유계
적당한 양수 K와 C가 있어 |z| ≥ c이면 | p(z) | ≥ K|z|n임을 보이자.
|z| ≥ 1일 때 |an-1 zn-1 + ··· + a0| ≤ (|an-1| + ··· + |a0|) |z|n-1이다.
c > 0을 c = max { 1, 2( |an-1| + ··· + |a0| ) / |a0| }, K = |a0|/2이라 하면
|z| ≥ c일 때, |p(z)| ≥ |a0| |z|n - (|an-1| + ··· + |a0|) |z|n-1
|z| ≥ c일 때, |p(z)| ≥ |a0| |z|n - |a0| |z|n/2
|z| ≥ c일 때, |p(z)| ≥ K |z|n
○ 풀이 : 최대·최소 정리
함수 φ : ℝ2 → ℝ이 φ(x, y) = | p(x + yi) |일 때, φ가 연속함수이며 어떤 z0 = x0 + y0i에서 최솟값을 가짐을 보이자.
(단, z = x + yi = (x, y)로 표기한다.)
함수 φ(x, y) = | p(x, y) |가 연속인 것은, | φ(x, y) - φ(u, v) | ≤ | p(x + yi) - p(u + vi) |이고 p(x + yi)가 연속이기 때문이다.
단계 1로부터 c, K > 0이 있어 |z| ≥ c이면 φ(z) ≥ K|z|n이다.
이때, D = {z ∈ ℂ | |z| ≤ c}라 하면 D는 유계인 닫힌 집합이다.
따라서 최대·최소 정리에 의해 φ(x0, y0) ≤ φ(D)인 (x0, y0)가 존재한다.
이로부터 φ(z0) ≤ φ(ℂ)이다.
④ 단계 2. φ(x0, y0) = 0이면 증명이 된다. φ(x0, y0) ≠ 0이라고 가정하고 모순을 이끌자. 먼저 다음을 만족하는 다항식 q(z)가 존재함을 보이시오.
○ 모든 z ∈ ℂ에 대해 |q(z)| ≥ 1○ 0<m ≤ n과 bm, ···, bn ∈ ℂ, bm ≠ 0이 있어 q(z) = 1 - bm zm + ··· + bn zn이다.
○ 풀이
φ(x0, y0) = 0이면 증명이 된다. φ(x0, y0) ≠ 0이라고 가정하고 모순을 이끌자.
p(z) = anzn + ··· + a0일 때, q(z) = p(z0 - z) / /p(z0)라 하면,
i. 모든 z ∈ ℂ에 대해 |q(z)| ≥ 1이다.
ii. q(0) = 1이고, q(z)는 n차이므로 0 < m ≤ n과 bm, ···, bn ∈ ℂ, bm ≠ 0이 있어
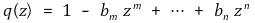
⑤ 단계 3. bm = (r cos θ, r sin θ)라 할 때 ε > 0이 있어 z = (ε cos (-θ / m), ε sin (-θ / m))라 할 때 |q(z)| < 1임을 보이시오.
○ 풀이
bm = r(cos θ + i sin θ)로 표현할 수 있다.
z = ε (cos (-θ/m), sin (-θ/m))일 때,
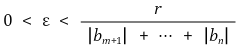
일 경우
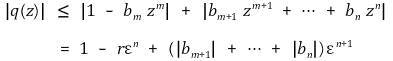
이므로 단계 2의 i.에 모순이다.
⑵ 예제 : p(x) = anxn + ··· + a1x + a0가 실계수 n차 다항식이면 p(x)는 유한 개의 다항식 p1(x), ···, pk(x)과 상수 an의 곱이 되며, 여기서 각 pi(x)는 x - b나 x2 - cx + d 꼴임을 보이시오. 여기서 b, c, d ∈ ℝ이고 c2 < 4d이다.
⑶ Descartes 규칙 : p(x) = anxn + ··· + a0가 실계수 n차 다항식으로 p(0) ≠ 0이다. ν를 a0, ···, an에서 부호의 변화의 개수라 하자. 또한 μ를 p(x)의 중근을 포함한 양의 근의 개수라 하면 μ ≤ ν이고 μ - ν는 짝수임을 보이시오.
입력: 2019.12.26 14:06
수정: 2024.09.06 13:46
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 8강. 미분과 편미분 (0) | 2020.01.01 |
|---|---|
| 【해석학】 7강. 고정점 정리 (1) | 2019.12.26 |
| 【해석학】 4강. 연속성 (3) | 2019.12.26 |
| 【해석학】 3강. 증가수열과 코시수열 (21) | 2019.12.25 |
| 【해석학】 2강. 집합의 크기 (14) | 2019.12.24 |




최근댓글