8강. 미분과 편미분
추천글 : 【해석학】 해석학 목차
1. 일변수함수의 미분 [본문]
2. 다변수함수의 미분 [본문]
풀이가 궁금하시면 답변 바랍니다.
1. 일변수함수의 미분 [목차]
⑴ 일변수함수의 미분의 정의
① f : (a, b) → ℝ와 c ∈ (a, b)에 대해 f가 c에서 미분가능하다는 것은 실수 ℓ이 있어 임의의 ε > 0에 대해 δ > 0이 있어

일 때마다 다음이 성립한다는 것

② n계 도함수 f(n)이 존재하고 연속인 함수 f를 Cn 함수라고 함
⑵ 평균값 정리 등
① 롤의 정리(Rolle's theorem) : f : ℝ → ℝ가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분가능하며 f(a) = f(b)일 때, f'(c) = 0이 되는 c ∈ (a, b)가 존재한다.
○ 풀이
최대·최소 정리에 의해 [a, b]에서 f(x)의 최댓값 M과 최솟값 m이 존재한다.
case 1. M = m인 경우
f(x)는 [a, b]에서 상수함수이다.

case 2. M ≠ m인 경우
f(a) = f(b) = t에 대해, M과 m 중 하나는 적어도 t와 다르다.
case 2-1. M ≠ t인 경우
f(c1) = M인, c1 ∈ (a, b)가 존재한다.
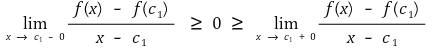
그런데 f(x)는 미분가능하므로 다음이 성립한다.
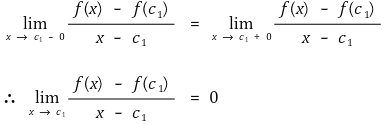
case 2-2. m ≠ t인 경우
f(c2) = m인, c2 ∈ (a, b)가 존재한다.
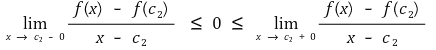
그런데 f(x)는 미분가능하므로 다음이 성립한다.
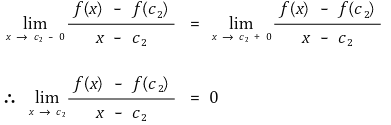
그러므로 주어진 조건에서 f'(c) = 0이 되는 c ∈ (a, b)가 존재한다.
② 평균값 정리(mean value theorem) : 함수 f : [a, b] → ℝ이 연속이고 각 x ∈ (a, b)에서 미분가능하면 f(b) - f(a) = f'(c)(b-a)인 a < c < b가 존재함을 증명하라.
○ 풀이
다음과 같은 함수 g(x)를 정의하자.

이때 g(a) = g(b) = f(a)이므로 g(x)에 대해 롤의 정리를 적용할 수 있다.
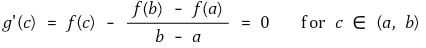
③ 코시의 평균값 정리(Cauchy's mean value theorem) : 구간 [a, b]에서 정의된 함수 f, g가 [a, b]에서 연속이며 (a, b)에서 미분가능하다. 그러면, f'(x0) (g(b) - g(a)) = g'(x0) (f(b) - f(a))가 성립하는 x0 ∈ (a, b)가 존재한다.
○ 풀이
F(x) = f(x) (g(b) - g(a)) - g(x) (f(b) - f(a))를 생각하자.
F(a) = f(a) (g(b) - g(a)) - g(a) (f(b) - f(a)) = f(a)g(b) - f(b)g(a)
F(b) = f(b) (g(b) - g(a)) - g(b) (f(b) - f(a)) = f(a)g(b) - f(b)g(a)
F(a) = F(b)이므로 롤의 정리에 의해,
F'(x0) = f'(x0) (g(b) - g(a)) - g'(x0) (f(b) - f(a)) = 0인 x0 ∈ (a, b)가 존재한다.
④ 다르부 정리(theorem of Darboux, 다브루 정리, 다부르 정리) : 함수 f : ℝ → ℝ가 있을 때, 구간 [a, b] 위의 모든 점에서 f'(x)가 존재하고 f'(a) ≠ f'(b)라고 가정하자. f'(a)와 f'(b) 사이에 존재하는 임의의 실수 γ (≠ f'(a), f'(b))에 관하여 f'(c) = γ를 만족하는 점 c ∈ (a, b)가 존재함을 증명하라.
○ 풀이
g(x) ≡ f(x) - γ(x - a), g'(x) = f'(x) - γ
g(x)는 연속이면서 미분가능한 함수이므로 최대최소정리에 의해 구간 [a, b]에서 최댓값과 최솟값을 가짐
case 1. f'(a) < γ < f'(b)
g'(a) = f'(a) - γ < 0, g'(b) = f'(b) - γ > 0이므로 최소점 c가 존재함을 알 수 있다.
g'(c) = f'(c) - γ = 0 (∵ 미분의 정의)
case 2. f'(b) < γ < f'(a)
g'(a) = f'(a) - γ > 0, g'(b) = f'(b) - γ < 0이므로 최대점 c가 존재함을 알 수 있다.
g'(c) = f'(c) - γ = 0 (∵ 미분의 정의)
참고로 f'(x)가 연속이라는 가정을 요하지 않으며 다르부의 중간값 정리라고도 한다.
⑤ 로피탈 정리(L'Hospital's theorem) : 미분가능한 두 함수 f, b에 대하여
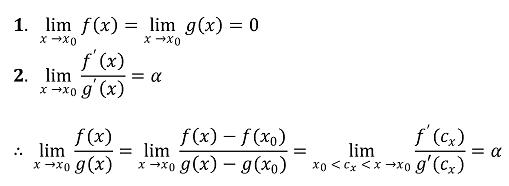
⑶ 역함수정리
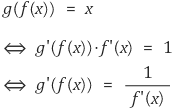
⑷ 음함수정리

⑸ 볼록함수와 오목함수
① 볼록집합(convex set) : 임의의 두 점을 양끝으로 하는 선분의 모든 점이 항상 해당 집합의 원소인 경우
② 볼록함수(convex function) :{(x, y) | y ≥ f(x)}가 볼록집합인 함수
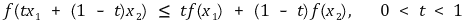
○ 아래로 볼록을 의미
○ 가로축에 대해서 볼록하다는 의미
③ 강볼록함수(strictly convex function)

④ 오목함수(concave function) :{(x, y) | y ≤ f(x)}가 볼록집합인 함수
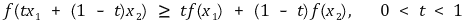
○ 위로 볼록을 의미
○ 가로축에 대해서 오목하다는 의미
⑤ 강오목함수(strictly concave function)
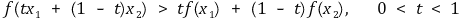
⑥ 선형함수(linear function) : 볼록함수이자 오목함수
⑦ 볼록성과 이차도함수의 관계
○ f"(x) ≥ 0인 것과 볼록함수인 것은 필요충분이고, f"(x) ≤ 0인 것과 오목함수인 것은 필요충분
○ 증명 1.
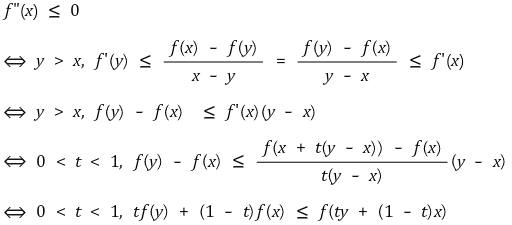
○ 증명 2. 볼록함수의 경우 f"(x) ≥ 0이고 오목함수의 경우 f"(x) ≤ 0이 성립함을 보이는 쉬운 증명
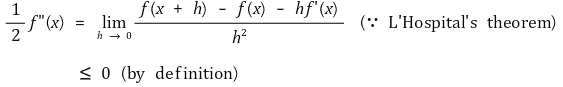
○ 반례 : 강오목함수라고 하여 f"(x) < 0인 것은 아님
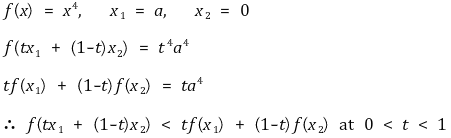
⑹ 일변수함수의 테일러급수
① 조건 : a ∈ ℝ를 포함하는 적당한 열린구간 I에서 정의된 함수 f : I → ℝ에 대하여 f(n)이 연속이고 미분가능
② 정리 : 다음 관계식을 만족시키는 cx가 a와 x 사이에 존재함
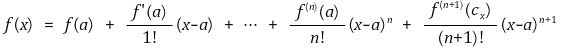
③ 해석함수
○ 정의 : 테일러 급수가 원래 함수와 같은 경우
○ 해석함수가 아닌 예 : 이 예는 원점에서 무한번 미분가능하지만 (무한급함수) 테일러 급수인 0과 원래 함수가 다름
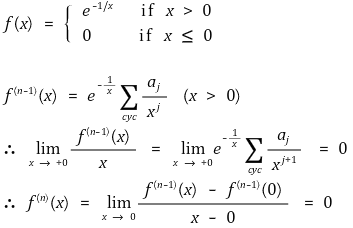
④ 평균값 정리의 확장에 의해 임의의 함수 f, g에 의해 다음 관계식을 발견할 수 있음
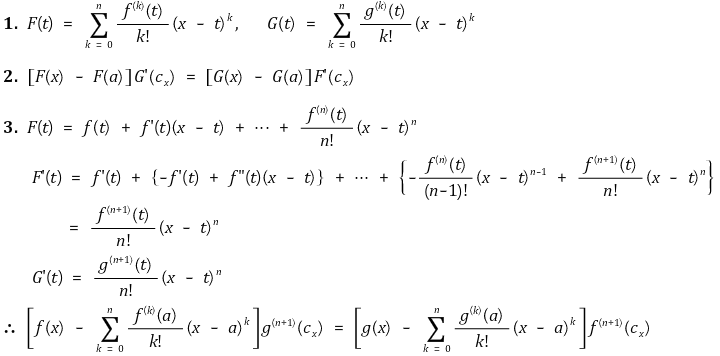
⑤ g(x) = (x-a)xn+1이라고 두면 다음 관계식을 발견할 수 있음
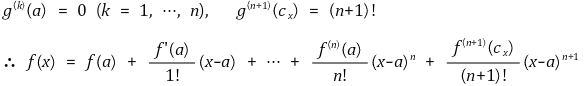
⑺ 벡터와 일변수 미분
① 벡터의 내적과 일변수 미분
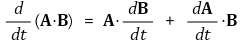
② 벡터의 외적과 일변수 미분
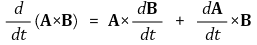
2. 다변수함수의 미분 [목차]
⑴ 다변수함수
① 동차함수(homogeneous function) : 함수 f : ℝn → ℝ이 고정된 자연수 k에 대해 다음과 같을 때 k차 동차함수라 함
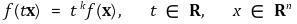
⑵ 다변수함수의 미분가능성
① 집합 D ⊆ ℝk와 u0 ∈ ℝk이 있어 모든 δ > 0에 대해 0 < |u - u0| < δ인 u ∈ D가 있다고 하자. 이때 함수 g : D → ℝℓ가 u0 ∈ ℝk에서 극한 v ∈ ℝℓ를 갖는다는 것은 각 ε > 0에 대해 δ > 0가 있어 u ∈ D, 0 < |u - u0| <δ일 때마다 |g(u) - g(u0)| < ε라는 것이다. 이때
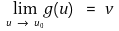
과 같이 나타낸다.
② 열린집합 D ⊆ ℝ2와 함수 f : D → ℝ가 있다. 이때 f가 (x0, y0) ∈ D에서 미분가능하다는 것은 실수 ℓ, m이 있어
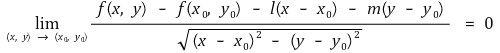
과 같다는 것이다. 이때 ℓ, m이 유일함을 보일 수 있는데 f'(x0, y0) = [ℓ, m]이라 쓴다.
③ 예제 : f가 (x0, y0)에서 미분가능할 경우 f가 두 편도함수를 가지며 fx(x0, y0) = ℓ, fy(x0, y0) = m임을 보이시오. 따라서 ℓ, m이 유일하다.
④ 예제 : 열린집합 D ⊆ ℝk와 함수 f : D → ℝ에 대해 미분은 어떻게 정의하겠는가? D ⊆ ℝk이고 함수 f : D → ℝℓ일 때도 정의를 할 수 있는가?
⑶ 다변수함수의 미분의 정의
① 기본 연산
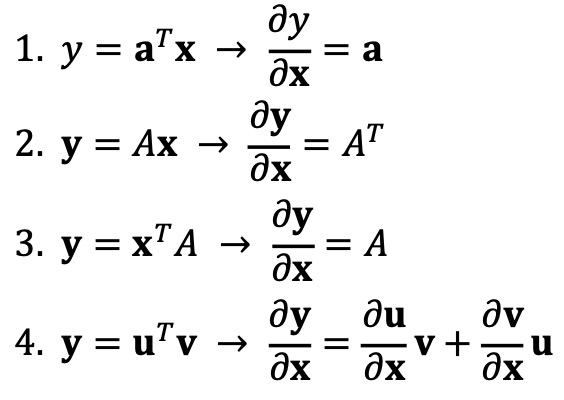
② 야코비 행렬(Jacobian matrix) : 영역 Ω ⊂ ℝn에서 정의된 함수 F = (f1, ···, fm)' : Ω → ℝm가 점 p ∈ Ω에서 미분가능하다고 했을 때 야코비 행렬을 다음과 같이 정의함
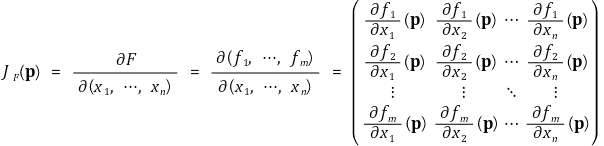
③ 헤세 행렬(Hessian matrix)
○ 2 × 2 행렬의 헤세 행렬
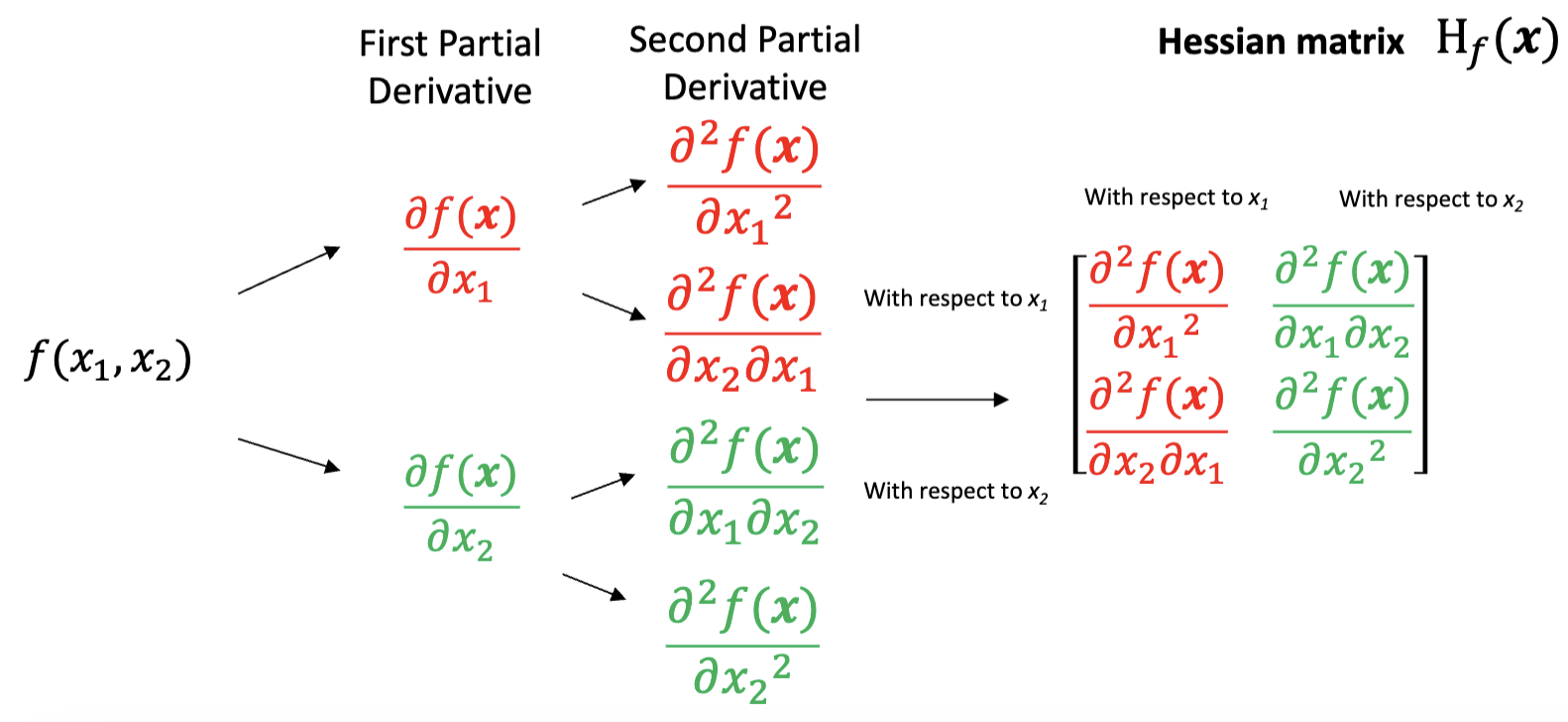
○ 3 × 3 행렬의 헤세 행렬
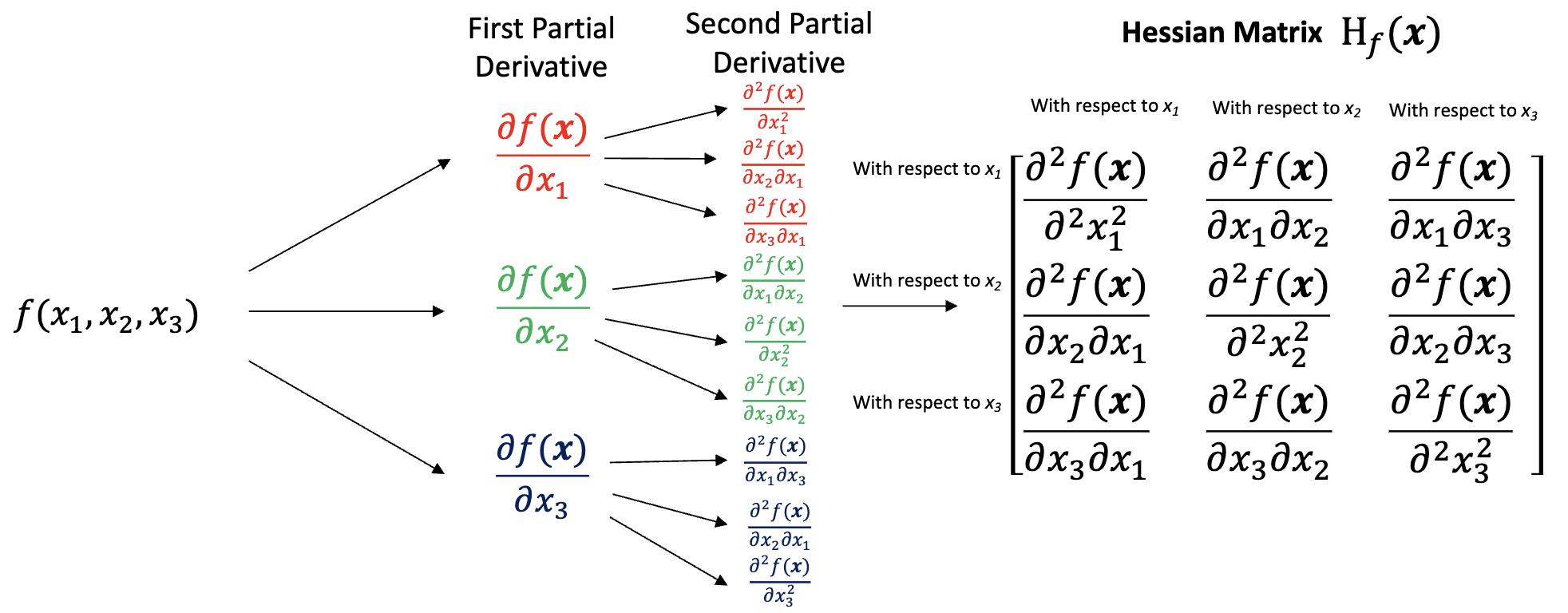
○ n × n 행렬의 헤세 행렬
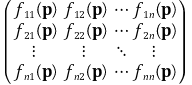
④ 그래디언트(gradient)

⑤ 전미분
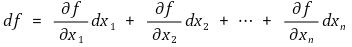
⑷ 방향미분과 편미분
① D ⊆ ℝ3가 열린집합으로 u ∈ D, v ∈ ℝ3가 |v| = 1일 때, 함수 G : D → ℝ가 u에서의 방향미분 ℓ = DvG(u)은 다음과 같음
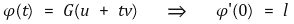
② 편도함수
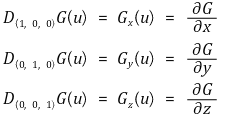
③ 예제 : 방향미분을 변수가 2개인 함수에 대해 정의하고 그 기하학적 의미를 설명하시오.
④ 예제 : 함수 g : D → ℝ에 대해
을 정확히 정의하고 기본 법칙들을 찾아 증명하시오.
⑤ 예제 : f : (a, b) → ℝ가 c ∈ (a, b)에서 미분가능하면 f가 c에서 연속임을 보이시오.
⑥ 예제 : f : (a, b) → ℝ가 u ∈ (a, b)에서 미분가능하고 g : (c, d) → ℝ가 v = f(u) ∈ f((a, b)) ⊆ (c, d)에서 미분가능하다고 하자. 이때 합성함수 h : (a, b) → ℝ도 u에서 미분가능하며
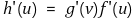
을 만족함을 보이시오.
⑦ 예제 : f, g : (a, b) → ℝ가 c ∈ (a, b)에서 미분가능하면 fg도 c에서 미분가능함을 보이시오.
⑧ 예제 : f : (a, b) → (c, d)가 증가하는 전단사함수로 u ∈ (a, b)에서 미분가능하며 f'(u) ≠ 0이다. 이때 역함수 g가 v = f(u)에서 미분가능하며 g'(v) = 1 / f'(u)임을 보이시오. g(x) = x⅓일 때 g'(8)을 구할 수 있는가?
⑨ 예제 : 열린집합 D ⊆ ℝ3의 각 점에서 함수 f1, f2 : D → ℝ가 편도함수들을 갖고, u0 ∈ D에서 연속하면 f = [f1, f2]T가 u0에서 미분가능함을 보이시오.
⑩ 예제 : 열린집합 D ⊆ ℝ2의 각 점에서 함수 f : D → ℝ가 편미분 fxy, fyx를 갖고 u0 ∈ D에서 연속이면 fxy(u0) = fyx(u0)임을 보이시오.
⑪ 예제 : 함수 f : ℝ2 → ℝ을 f(0, 0) = 0, f(x, y) = xy / (x2 + y2), (x, y) ≠ (0, 0)으로 정의하면 fx, fy가 모든 점에서 존재하나 함수 f 자신은 원점에서 연속이 아님을 보이시오. 함수 g를 g(0, 0) = 0, g(x, y) = xy(x2 - y2) / (x2 + y2)이라고 하면 gxy, gyx가 모두 연속인가?
⑫ 예제 : 함수 f : (a, b) → ℝ3와 g : D → ℝ가 있다. 여기서 D ⊆ ℝ3는 f((a, b))를 포함하는 열린집합이다. f가 c ∈ (a, b)에서 미분가능하고 g가 u = f(c)에서 미분가능하면 h = g∘ f도 c에서 미분가능하고 f = [f1, f2, f3]T로 쓸 때
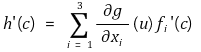
을 만족함을 보이시오.
⑬ 예제 : 위에서 gradient를 ∇g = (∂g / ∂x1, ∂g / ∂x2, ∂g / ∂x3)라 정의할 때 v ∈ ℝ3가 |v| = 1에 대해 방향미분 Dvg(u)은 Dvg(u) = v·∇g(u) = |∇g(u)| cos θ가 됨을 보이시오. 여기서 θ는 두 벡터 v, ∇g(u) 사이의 각이다. 어떠한 v에 대해 Dvg(u)가 최대가 되는가?
⑸ 연쇄법칙(chain rule)
① 라이프니츠 표기법을 이용한 다변수함수 미분의 연쇄법칙
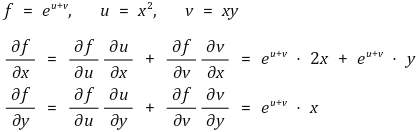
② 야코비 행렬을 이용한 다변수함수의 미분의 연쇄법칙
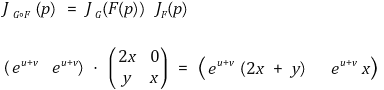
⑹ 역함수 정리
① det[JF(G(y))] ≠ 0에 대하여,
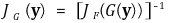
② (주석) 역함수의 도함수는 야코비 행렬의 역함수로 구할 수 있다는 의미
③ 예제
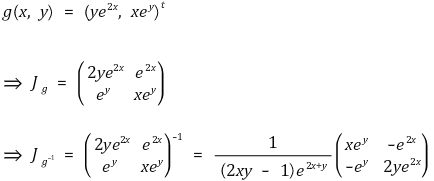
⑺ 음함수 정리
① 정리
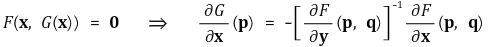
② 이변수함수인 경우 : 함수 f(x, y)가 열린집합 (a, b) ∈ D 위에서 정의되고 연속인 fx, fy : D → ℝ를 갖는다. f(a, b) = 0, fy(a, b) ≠ 0이면 ε, δ > 0와 함수 φ : (a - δ, a + δ) → (b - ε, b + ε)이 있어 다음 조건을 만족한다.
○ U = (a - δ, a + δ) × (b - ε, b + ε) ⊆ D
○ φ(a) = b
○ 각 |x - a| < δ에 대해 f(x, φ(x)) = 0임
○ (x, y) ∈ U이고 f(x, y) = 0이면 y = φ(x)
○ φ는 연속인 1차 편미분을 가짐
③ 예제 : 위 정리에서 φ가 1차 편미분을 가짐을 보이시오.
④ 예제
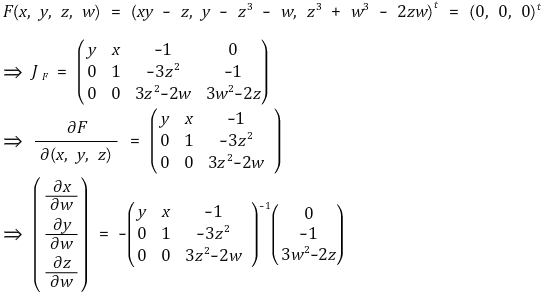
⑻ 다변수함수의 볼록성 : 준볼록함수와 준오목함수
① 준볼록함수(quasi-convex function) : ℝn의 볼록 부분집합 Ω에서 정의된 함수 f : Ω → ℝ에 대하여,
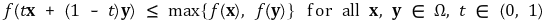
② 준오목함수(quasi-concave function) : ℝn의 볼록 부분집합 Ω에서 정의된 함수 f : Ω → ℝ에 대하여,
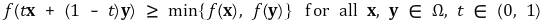
③ 위 정의에서 등호가 없는 경우를 강준오목함수(strictly quasi-concave function), 강준볼록함수(strictly quasi-convex function)라고 함
④ f : Ω → ℝ가 준볼록함수 ⇔ 임의의 실수 a ∈ ℝ에 대하여 집합 Ca- ≡ {x ∈ Ω : f(x) ≤ a}가 볼록집합
⑤ f : Ω → ℝ가 준오목함수 ⇔ 임의의 실수 a ∈ ℝ에 대하여 집합 Ca+ ≡ {x ∈ Ω : f(x) ≥ a}가 볼록집합
⑼ 다변수 함수의 테일러 급수
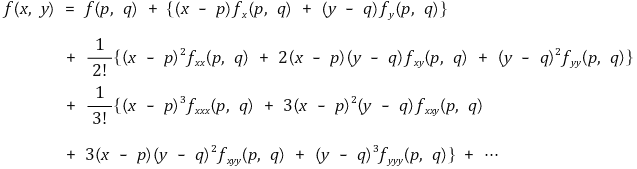
⑽ 조화함수
① 열린집합 D ⊆ ℝ2 위에서 함수 g : D → ℝ가 연속인 gxx, gxy, gyx, gyy를 갖고 gxx + gyy = 0일 때 조화함수라고 한다.
② 예로 g(x, y) = x2 - y2은 조화함수이다.
③ 예제 : 함수 g : ℝ2 → ℝ가 조화함수라 하자. x = r cos θ, y = r sin θ라 하면 r, θ에 관한 함수 h(r, θ) = g(r cos θ, r sin θ)가 생긴다. 이때 h는
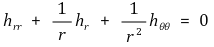
을 보이시오.
④ 예제 : 반평면 D ={(x, y) | y > 0}에서의 각 점 (x, y)에서 0 < θ < π를 벡터 (x, y)이 양의 x축과 이루는 각이라 하면 θ는 조화함수임을 보이시오.
⑾ 직교좌표계와 극좌표계의 관계식
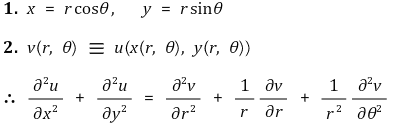
입력: 2020.01.01 21:15
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 10강. 적분 (0) | 2020.01.07 |
|---|---|
| 【해석학】 9강. 라그랑주 승수법 (0) | 2020.01.06 |
| 【해석학】 7강. 고정점 정리 (1) | 2019.12.26 |
| 【해석학】 6강. 대수학의 기본정리 (0) | 2019.12.26 |
| 【해석학】 4강. 연속성 (3) | 2019.12.26 |




최근댓글