10강. 적분
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 리만 적분 [본문]
2. 푸비니 정리 [본문]
3. 유한 개의 불연속점만을 가지는 함수는 적분 가능함을 증명 [본문]
4. 미적분학 기본정리 [본문]
1. 리만 적분(Riemann integration) [목차]
⑴ 구간 [a, b]의 한 분할이란 유한집합 {a, b}⊆ ℙ ⊆ [a, b]이다.
⑵ 직사각형 R = [a, b] × [c, d]의 분할이란 ℙ = ℙ1 × ℙ2로 여기서 ℙ1은 [a, b]의 분할, ℙ2는 [c, d]의 분할이다.
⑶ ℙ를 ℙ로 나누어 생기는 선분이나 직사각형의 모임으로 보기로 하자. 예를 들면, ℙ가 [0, 1]의 분할로 ℙ ={0, 0.3, 0.7, 1}이면 ℙ를 {[0, 0.3], [0.3, 0.7], [0.7, 1]}로 보기로 한다. 또한 ℙ가 [0, 1] × [0, 2]의 분할 {0, 0.3, 0.7, 1}×{0, 1, 2}라면 ℙ ={[0, 0.3] × [0, 1], [0, 0.3] × [1, 2], [0.3, 0.7] × [0, 1] , [0.3, 0.7] × [1, 2], [0.7, 1] × [0, 1], [0.7, 1] × [1, 2]}로 보기로 한다.
⑷ 두 분할 ℙ, ℚ에 대해 ℙ ⊆ ℚ이면 각 직사각형 또는 선분 P ∈ ℙ는 ℚ에서의 직사각형 또는 선분들로 분할됨을 알 수 있다.
⑸ ℙ가 직사각형 R의 분할일 때 ℙ의 선택이란 한 함수 r : ℙ → R로 각 P ∈ ℙ에 대해 r(P) ∈ P인 것이다. 이때 함수 f : R → ℝ가 있으면 Riemann 합 S(f, ℙ, r)을 모든 P ∈ ℙ에 대해
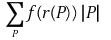
로 정의한다. 여기서 |P|는 직사각형 P의 넓이이다.
⑹ 직사각형 R에 대해 함수 f : R → ℝ가 적분가능하다는 것은 실수 I가 있어 각 ε > 0에 대해 R의 분할 ℙ0가 있어 부등식 |I - S(f, ℙ, r)| < ε이 모든 R의 분할 ℙ ⊇ ℙ0와 ℙ의 선택 r에 대해 성립하는 것이다. 이때 이러한 I는 유일한데 다음과 같이 쓴다.

⑺ 예제 : 함수 f : [a, b] → ℝ와 g : [a, b] × [c, d] × [p, q] → ℝ가 적분가능하다는 것을 정의하라.
⑻ 예제 : R = [0.2] × [0, 1]이고 f : R → ℝ가 상수함수 f(x, y) = [x]이면 f는 적분가능한가? 여기서 [x]는 x 이하인 가장 큰 정수이다.
⑼ 예제 : f : [0, 1] × [0, 1] → ℝ이 x ∈ ℚ이면 f(x, y) = 1, x ∉ ℚ이면 f(x, y) = 0으로 정의하면 f는 적분가능하지 않음을 보이시오.
⑽ 부분적분법
① 정의 : ∫ u'v = uv - ∫uv'
② 유용한 팁 : 다항함수와 초월함수가 결합된 복잡한 함수의 적분의 경우 다항함수를 미분하는 방향으로 부분적분법을 전개하면 됨

2. 푸비니의 정리(Fubini's theorem) [목차]
⑴ 중적분을 변수가 하나인 함수의 적분으로 계산하게 함
⑵ 직사각형 R = [a, b] × [c, d]에 대해 함수 f : R → ℝ가 적분가능하다. 또한 각 x ∈ [a, b]에 대해 적분
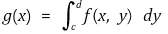
가 존재한다고 하자. 이때
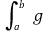
가 존재하며
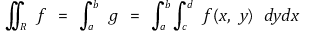
임을 보이시오.
⑶ 예제 : 함수 f : E = [a, b] × [c, d] × [p, q] → ℝ가 적분가능하고 각 (x, z) ∈ [a, b] × [p, q]에 대해 적분
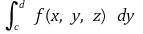
가 존재하면
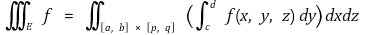
임을 보이시오.
3. 유한 개의 불연속점만을 가지는 함수는 적분 가능함을 증명 [목차]
⑴ 리만 조건(Riemann condition) : 함수 f : R → ℝ가 각 ε > 0마다 분할 ℙ가 있어 부등식 |S(f, ℚ1, r2) - S(f, ℚ2, r2)| < ε에 대해 분할 ℚ1, ℚ2 ⊇ ℙ이고 ri가 ℚi의 선택일 때마다 성립한다고 하면 f가 적분가능함을 보이시오.
⑵ 예제 : A ⊆ ℝ가 유계이고 닫혀있으며 함수 f : A → ℝ가 연속이면 각 ε > 0에 대해 δ > 0가 있어 x, y ∈ A, |x - y| < δ일 때마다 |f(x) - f(y)| < ε이 성립함을 보이시오.
⑶ 예제 : 유계인 함수 f : [a, b] → ℝ가 유한 개의 점에서만 불연속이고 유계이면 적분가능함을 보이시오.
4. 미적분학 기본정리 [목차]
⑴ 미적분학 기본정리 1. 함수 f : [a, b] → ℝ가 적분가능하며 함수 F : [a, b] → ℝ는 연속으로 각 x ∈ (a, b)에 대해 F'(x) = f(x)이다. 이때
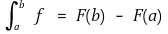
를 보이시오.
⑵ 미적분학 기본정리 2. 함수 f : [a, b] → ℝ가 연속이라고 하자. 각 x ∈ (a, b)에 대해
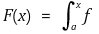
라 하면 각 a < x < b에 대해 F'(x) = f(x)임을 보이시오. a와 b점에서는 무슨 말을 할 수 있는가?
입력 : 2020.01.07 19:18
수정: 2024.12.28 17:42
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 14강. 그린정리 (0) | 2020.01.10 |
|---|---|
| 【해석학】 12강. 선적분 (0) | 2020.01.10 |
| 【해석학】 9강. 라그랑주 승수법 (0) | 2020.01.06 |
| 【해석학】 8강. 미분과 편미분 (0) | 2020.01.01 |
| 【해석학】 7강. 고정점 정리 (1) | 2019.12.26 |




최근댓글