14강. 그린정리(Green theorem)
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 그린정리 [본문]
2. 조화함수가 평균값 성질을 가짐을 증명 [본문]
1. 그린정리 [목차]
⑴ 선적분의 정의
① D ⊆ ℝ2에 대해 함수 F : D → ℝ2를 하나의 벡터장이라고 한다. 매개곡선 c : [a, b] → ℝ2와 c로 방향이 주어지는 유향곡선 C = c([a, b])에 대해 벡터장 F : C → ℝ2가 유향곡선 C 위에서 벡터 선적분이 가능하다는 것은 실수 I가 있어 임의의 ε > 0에 대해 [a, b]의 분할 ℙ가 있어 ℙ ⊆ {a = t0 < ··· < tn = b} , ti-1 ≤ τi ≤ ti일 때마다

라는 것이다.
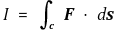
라 쓴다. F(x, y) = (P(x, y), Q(x, y))일 때

를

라고도 쓴다.
② 예제 : d : [c, d] → ℝ2가 매개곡선으로 d([c, d]) = C = c([a, b])이면 전단사함수 φ : [c, d] → [a, b]가 있어 c ∘ φ = d이다. φ가 증가할 경우는
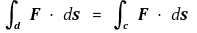
이고, φ가 감소할 경우에는
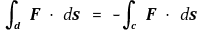
임을 보이시오.
③ 벡터 선적분
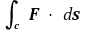
이 C의 방향을 유지하는 모든 매개곡선 c에 대해 같은 값을 가지므로 이 값을
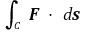
로 쓴다. 마찬가지로
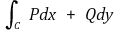
라 쓴다.
④ 예제 : 유향곡선 C가 매개곡선 c : [a, b] → ℝ2로 방향이 주어지고 c' : [a, b] → ℝ2이 연속이며 F : C → ℝ2가 연속인 벡터장이면 벡터 선적분
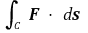
가 존재하고
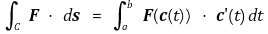
가 성립한다.
⑤ F(x, y) = (P(x, y), 0)일 때
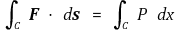
라 쓴다.
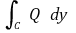
도 마찬가지이다.
⑥ 예제 : φ : [a, b] → ℝ가 연속이고 곡선 C가 매개곡선 c : [a, b] → ℝ2, c(t) = (t, φ(t))로 주어진다고 하자. 이때 P : C → ℝ가 연속이면 벡터 선적분
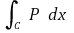
가 존재하고 그 값이
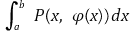
임을 보이시오.
⑵ 그린정리
① 개요
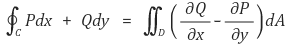
② 예제 : y-단순영역 D ⊆ ℝ2가 연속인 φ, ψ : [a, b] → [c, d]에 의해 D = {(x, y) | a ≤ x ≤ b, φ(x) ≤ y ≤ ψ(x)}로 주어진다. 여기서 φ ≤ ψ이다. D ⊆ U ⊆ ℝ2가 열린집합이고 P : U → ℝ가 연속이고 연속인 편미분
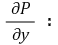
U → ℝ를 가지면
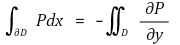
임을 보이시오. 여기서 ∂D는 영역을 왼쪽에 놓고 D의 경계를 도는 유향 폐곡선이다.
③ 예제 : D ⊆ ℝ2가 동시에 x-단순영역이고 y-단순영역이다. 그리고 P, Q가 D를 포함하는 열린 영역에서 연속인 1차 편미분들을 가지면
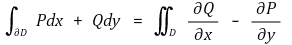
를 보이시오.
④ Green 정리 : D ⊆ ℝ2가 유한 개의 영역 D1, ···, Dn으로 분할되고 각 Di가 x-단순이면서 y-단순이라고 하자. P, Q가 D를 포함하는 열린영역에서 연속인 1차 편미분들을 가지면
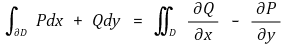
임을 보이시오.
⑶ 가우스 발산정리와의 등가성
① 열린집합 U ⊆ ℝ2에서 정의된 벡터장 F : U → ℝ2가 F(x, y) = (P(x, y), Q(x, y))로 주어질 때 그리고 P, Q가 1차 편미분을 가지면 div F : U → ℝ를
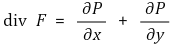
로 정의한다.
② 예제 : D와 P, Q가 ⑽과 같다고 하자. F를 F(x, y) = (P(x, y), Q(x, y))라고 하자. 각 (x, y) ∈ ∂D에 대해 바깥쪽 단위직교벡터를 n = n(x, y)라 하자. ∂D가 유한 개의 유향곡선 C1, ···, Cm으로 나뉘어지고 각 Ci는 매개화 ci : [ai, bi] → ℝ2를 가지며 ci'이 연속이고 ci'(t) ≠ 0이면,
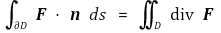
임을 보이시오.
③ 예제 : 함수 f : [a, b] × [c, d] → ℝ가 연속이면 함수 F : [c, d] → ℝ,
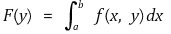
가 잘 정의되고 연속임을 보이시오.
④ Leibniz 규칙 : 함수 f : [a, b] × (c, d) → ℝ가 연속이고
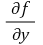
: [a, b] × (c, d) → ℝ도 존재하여 연속이면 F : (c, d) → ℝ를
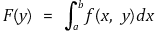
라 할 때 각 y ∈ (c, d)에 대해
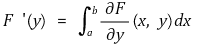
임을 보이시오.
2. 조화함수가 평균값 성질을 가짐을 증명 [목차]
⑴ u : ℝ2 → ℝ가 조화함수라는 것은 u가 연속인 2차 편도함수들을 가지며
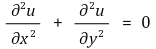
을 만족하는 것이다.
⑵ 예제 : u(x, y) = x2 - y2, v(x, y) = excos y는 조화함수임을 보이시오.
⑶ 예제 : u : ℝ2 → ℝ가 조화함수이다. I : [0, ∞) → ℝ을
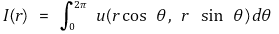
라 하면 I가 상수함수임을 보이시오.
⑷ 예제 : u : ℝ2 → ℝ가 조화함수이다. 각 r > 0에 대해
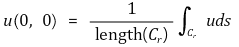
임을 보이시오. 여기서
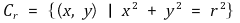
이다.
⑸ 예제 : u : ℝ2 → ℝ가 조화함수이다. 각 ρ > 0에 대해
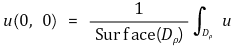
임을 보이시오. 여기서
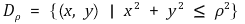
이다.
입력 : 2020.01.11 00:40
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 16강. 가우스 발산정리 (0) | 2020.01.11 |
|---|---|
| 【해석학】 15강. 스토크스 정리 (0) | 2020.01.11 |
| 【해석학】 12강. 선적분 (0) | 2020.01.10 |
| 【해석학】 10강. 적분 (0) | 2020.01.07 |
| 【해석학】 9강. 라그랑주 승수법 (0) | 2020.01.06 |




최근댓글