9강. 라그랑주 승수법 (라그랑지 승수법)
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 극소값, 극대값, 안장점 [본문]
2. 다변수함수가 국부적으로 최대값을 가질 충분조건 [본문]
3. 라그랑주 승수법 [본문]
4. FW 알고리즘 [본문]
1. 극소값, 극대값, 안장점 [목차]
⑴ 극값의 존재성 : 영역 Ω ⊂ ℝn에서 정의된 미분가능함수 f : Ω → ℝ이 점 p ∈ Ω에서 극대값이나 극소값을 가지면 ∇f(p) = 0임
⑵ (참고) 헤세 행렬(Hessian matrix)

⑶ (참고) 이차형식의 부호 정의 : 대칭행렬 A ∈ ℳn와 ℝn상의 모든 벡터 x ≠ 0에 대하여
① 양정부호 행렬(positive definite matrix)
○ A의 모든 고유치가 0보다 큼 ⇔ Q(x) > 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 > 0
② 양반정부호 행렬(positive semi-definite matrix)
○ A의 모든 고유치가 0보다 크거나 같음 ⇔ Q(x) ≥ 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 ≥ 0
③ 음정부호 행렬(negative definite matrix)
○ A의 모든 고유치가 0보다 작음 ⇔ Q(x) < 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 < 0
④ 음반정부호 행렬(negative semi-definite matrix)
○ A의 모든 고유치가 0보다 작거나 같음 ⇔ Q(x) ≤ 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 ≤ 0
⑤ 부정부호 행렬(indefinite matrix)
○ ① ~ ④와 달리 부호가 일정하지 않은 경우. A의 고유치 중 부호가 다른 게 존재
⑷ (참고) 이차형식의 부호 판정 : 대칭행렬 A ∈ ℳn과 {1, 2, ···, n}의 부분집합 S ={i1, i2, ···, ik}에 대하여
① 주소행렬(principal submatrix) : A에서 S에 해당하는 순서의 행과 열을 선택한 k × k 행렬

② 선도주소행렬(leading principal submatrix) : A의 마지막 n-k개의 행벡터와 열벡터를 생략하고 남은 k × k 행렬
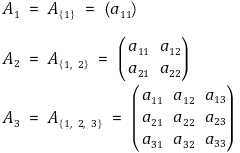
③ 정리 1. 대칭행렬 A ∈ ℳn가 양정부호인 것과 sgn(det(Ak)) = 1, k = 1, 2, ···, n인 것은 필요충분조건
④ 정리 2. 대칭행렬 A ∈ ℳn가 음정부호인 것과 sgn(det(Ak)) = (-1)k, k = 1, 2, ···, n인 것은 필요충분조건
⑤ 정리 3. 대칭행렬 A ∈ ℳn가 양반정부호인 것과 A의 모든 주소행렬식이 0 이상인 것은 필요충분조건
○ (주석) 정리 1 또는 2를 시도할 때 어느 선도주소행렬식이 0인 경우 정리 3을 시도함
○ 명백히 선도주소행렬식의 부호가 바뀌는 경우 부정부호행렬로서 정리 3 또는 4를 시도하지 않아도 됨
⑥ 정리 4. 대칭행렬 A ∈ ℳn가 음반정부호인 것과 -A의 모든 주소행렬식이 0 이상인 것은 필요충분조건
○ (주석) 정리 3을 시도하다가 주소행렬식의 부호가 일정하지 않으면 정리 4를 시도함
⑦ (참고) sgn은 판별식을 직접 계산하여 부호를 확인했을 때 양의 값이면 1, 음의 값이면 -1을 나타냄
⑧ 예제 : D ⊆ ℝ3가 열린집합이고 a = (a1, a2, a3) ∈ D이며 함수 f(x1, x2, x3)가 D 위에서 정의되어 있다. f가 a에서 국부최소값을 가질 충분조건을 찾고 그것을 증명하시오.
⑸ 영역 Ω ⊂ ℝn에서 정의된 C2 함수 f : Ω → ℝ이 점 p ∈ Ω에서 ∇f(p) = 0라 하면 다음이 성립
① Hf(p)가 양정부호행렬이면 f는 점 x = p에서 극소값을 가짐
② Hf(p)가 음정부호행렬이면 f는 점 x = p에서 극대값을 가짐
③ Hf(p)가 부정부호행렬이면 점 x = p는 f의 안장점
④ Hf(p)가 양반정부호행렬이면 f는 점 x = p에서 상대적 극소
⑤ Hf(p)가 음반정부호행렬이면 f는 점 x = p에서 상대적 극대
2. 다변수함수가 국부적으로 최대값을 가질 충분조건 [목차]
⑴ 예제 : A, B, C ∈ ℝ가 A, AC - B2 > 0을 만족한다고 하자. 이때 모든 (0, 0) ≠ (x, y) ∈ ℝ2에 대해 Ax2 + 2Bxy + Cy2 > 0임을 보이시오. 또한 M > 0이 있어 모든 (x, y) ∈ ℝ2에 대해 Ax2 + 2Bxy + Cy2 ≥ M(x2 + y2)임을 보이시오.
⑵ 예제 : f : (a, b) → ℝ가 n ∈ ℕ번째 도함수 f(n) : (a, b) → ℝ를 갖는다고 하자. 이때 c ∈ (a, b)에 대해 다항식 p(x)를
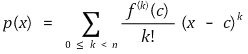
이라고 하자. 그러면 각 c ≠ x ∈ (a, b)에 대해 c와 x 사이에 x*이 있어
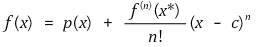
임을 보이시오.
⑶ 예제 : (a, b)가 열린집합 D의 한 점이고 함수 f : D → ℝ가 있다. f가 점 (a, b)에서 국부최소값을 가진다고 하자. 즉, δ > 0가 있어 (x, y) ∈ D, |(x, y) - (a, b)| < δ이면 f(a, b) ≤ f(x, y)이다. 이때 f가 점 (a, b)에서 편미분 fx(a, b), fy(a, b)을 가지면 fx(a, b) = fy(a, b) = 0임을 보이시오.
⑷ 예제 : (a, b)가 열린집합 D의 한 점이고 함수 f : D → ℝ가 있다. 함수 f가 연속인 fxx, fxy, fyx, fyy : D → ℝ를 갖고 이 편미분들이 점 (a, b)에서 fx = fy = 0이고 fxx, fxxfyy - (fxy)2 > 0이라 하자. 이때 δ > 0가 있어 (x, y) ∈ D, 0 > |(x, y) - (a, b)| < δ일 때마다 f(a, b) < f(x, y)임을 보이시오.
3. 라그랑주 승수법(Lagrange multiplier) [목차]
⑴ 개요
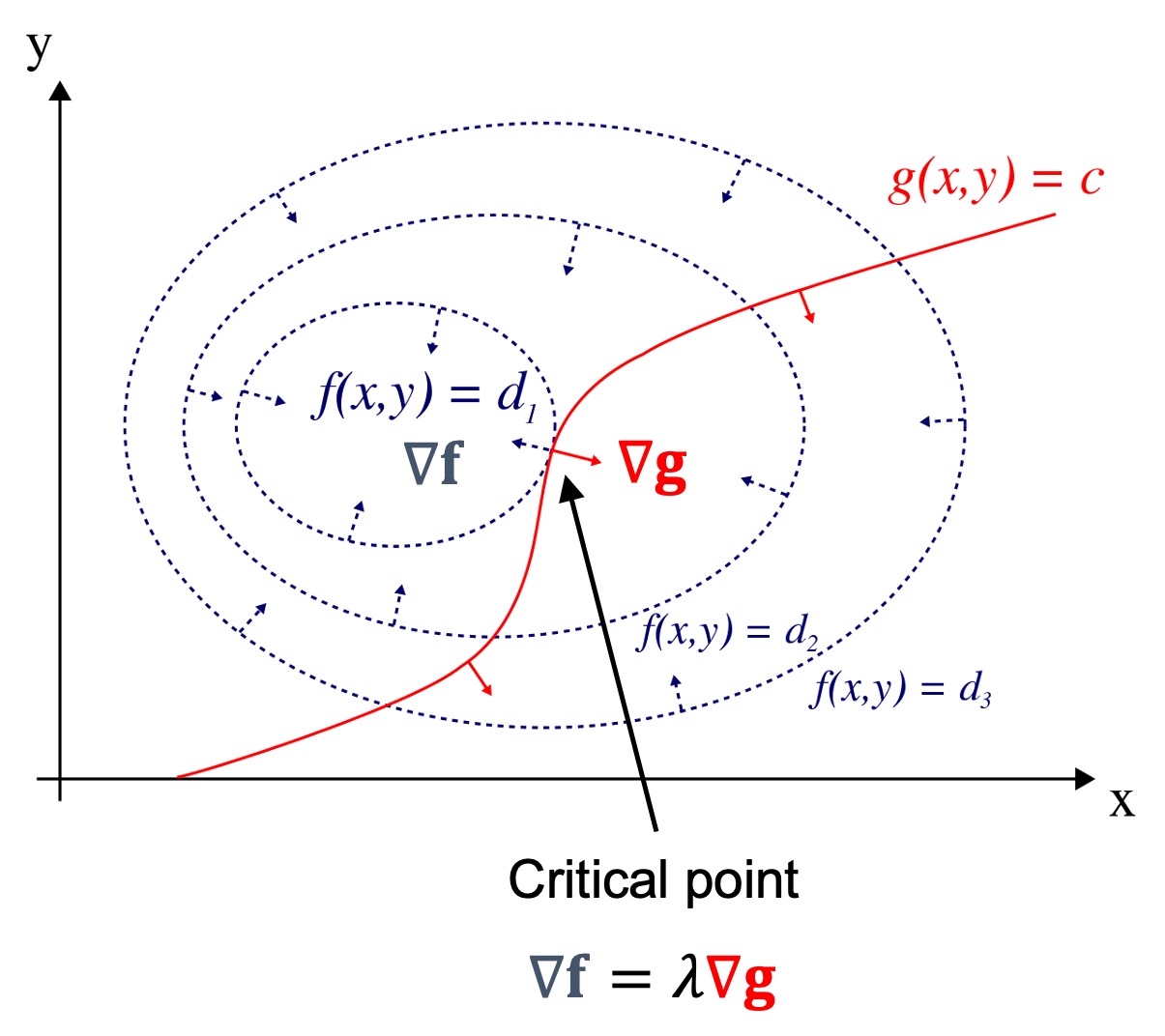
Figure. 1. 라그랑주 승수법 개념
⑵ 1개의 등식제약 하에서의 최적화 문제
① D ⊆ ℝk가 열린집합이고 a ∈ D일 때 f : D → ℝ의 a에서의 모든 편미분 fxi(a)가 존재하면 f의 a에서의 gradient를
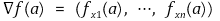
와 같이 정의한다.
② 함수 f, g : D → ℝ가 열린집합 D ⊆ ℝ2 위에서 연속인 1차 편미분을 갖는다. 또한 (a, b) ∈ D에서 g(a, b) = 0, ∇g(a, b) ≠ 0이다.
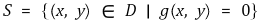
이라 하자. 만약 δ > 0가 있어 (x, y) ∈ S, |(x, y) - (a, b)| < δ일 때마다 f(a, b) ≤ f(x, y)라고 하면 λ ∈ ℝ가 있어 ∇f(a, b) = λ∇g(a, b)임을 보이시오.
③ 예제 : 함수 f : ℝ2 → ℝ가 f(x, y) = x2 + y2이고 D ={(x, y) | x2 + xy + y2 ≤ 1}일 때 D 위에서의 f의 최댓값과 최솟값을 구하시오.
풀이.
x2 + xy + y2 = c < 1을 만족하는 임의의 (xc, yc)에 대해, (x*, y*) = (xc / √c, yc / √c) ∈ D이고 f(xc, yc) < f(x*, y*)이다.
따라서, D* = {(x, y) | x2 + xy + y2 = 1} 위에서의 f의 최댓값이 D 위에서의 f의 최댓값과 동일하다.
그러므로 f의 최댓값은 라그랑주 승수법을 이용하면 f의 최댓값이 2임을 알 수 있다.
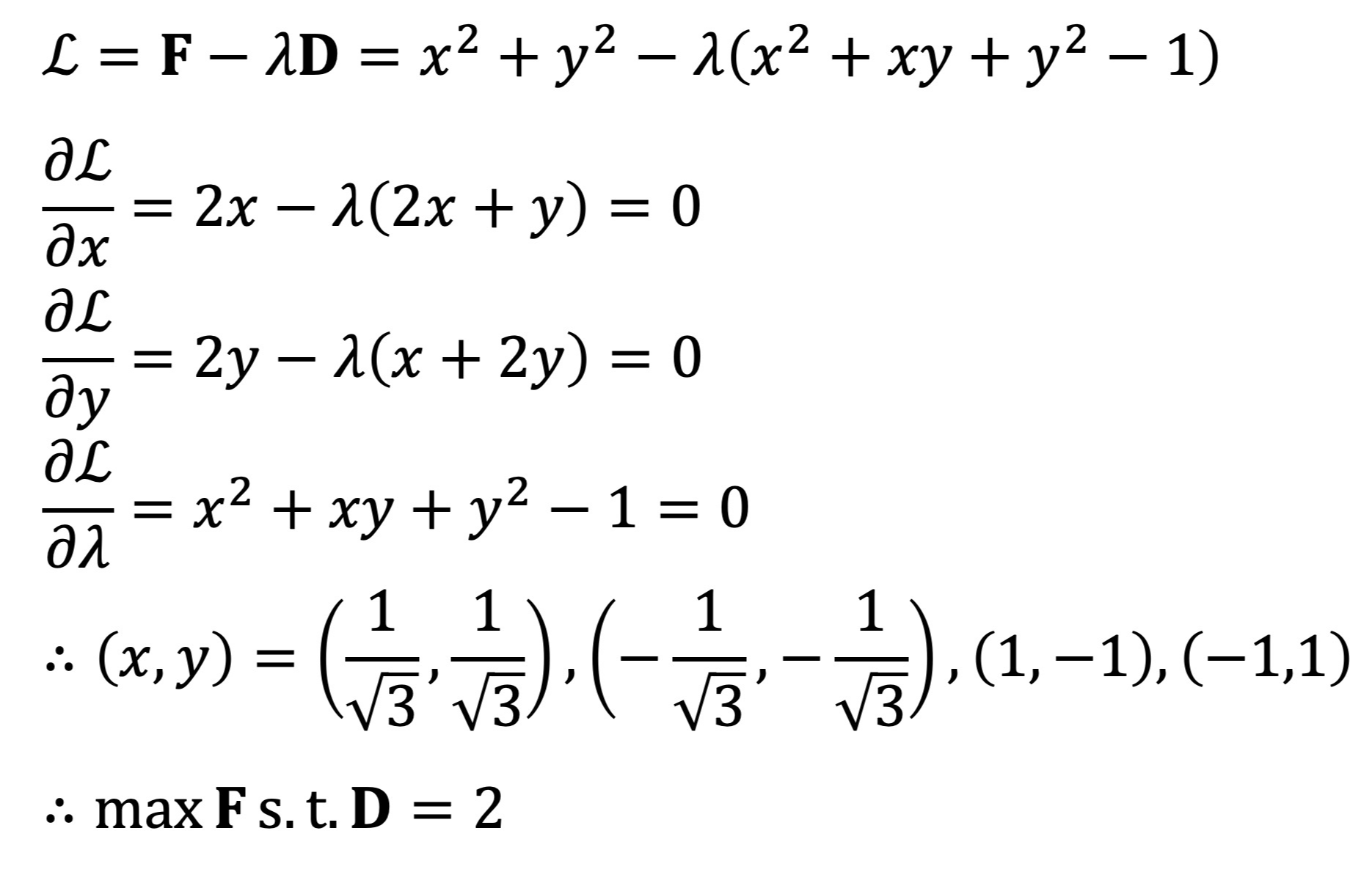
한편, f(x, y) ≥ 0, f(0, 0) = 0, (0, 0) ∈ D이므로 f의 최솟값이 0임을 알 수 있다.
④ 예제 : 음함수 정리와 라그랑주 승수법을 변수가 D ⊆ ℝk (k > 1)에서의 함수로 일반화하여 기술하여 보시오.
⑤ 예제 : 함수 f, g : D → ℝ이 열린집합 D ⊆ ℝ4 위에서 연속인 1차 편미분을 갖는다. 여기서 f(x, y, u, v)라 쓰자. (a, b, p, q) ∈ D이고 이 점에서 f = g = 0, fugv - fvgu ≠ 0이라고 하자. 이때 δ, ε > 0과 함수 (φ, ψ) : (a - δ, a + δ) × (b - δ, b + δ) → (p - ε, p + ε) × (q - ε, q + ε)이 다음 5가지 조건을 만족함을 보여라.
○ U = (a - δ, a + δ) × (b - δ, b + δ) × (p - ε, p + ε) × (q - ε, q + ε) ⊆ D
○ φ(a, b) = p, ψ(a, b) = q
○ 각 |x - a|, |y - b| < δ에 대해 (f, g)(x, y, φ(x, y), ψ(x, y)) = (0, 0)
○ (x, y, u, v) ∈ U, (f, g)(x, y, u, v) = (0, 0)이면 (u, v) = (φ(x, y), ψ(x, y))
○ φ와 ψ는 연속인 1차 편미분을 가짐
⑥ 예제 : (p, q) ∈ D ⊆ ℝ2가 열린집합이고 h, k : D → ℝ가 연속인 1차 편미분을 갖고 (a, b)에서 hukv - hvku ≠ 0이다. 여기서 (x, y) = (h(u, v), k(u, v))라 쓰자. 이때 열린집합 (p, q) ∈ V ⊆ D와 (h(a, b), k(a, b)) ∈ W ⊆ ℝ2가 있어 함수 (h, k) : V → W가 전단사함수이며 역함수를 (u, v) = (φ(x, y), ψ(x, y))라 쓰면 φ와 ψ도 연속인 1차 편미분을 가진다.
⑦ 예제 : (a, b, c) ∈ D ⊆ ℝ3가 열린집합으로 함수 f, g, h : D → ℝ가 연속인 1차 편미분들을 가지고 있으며 g(a, b, c) = h(a, b, c) = 0이다. 이때 δ > 0이 있어 다음 조건을 만족하면 다음 결론이 성립함을 보여라.
○ 조건 1. 두 벡터 ∇g(a, b, c), ∇h(a, b, c)가 원점과 함께 면적이 양인 삼각형을 이룸
○ 조건 2. (x, y, z) ∈ D, |(x, y, z) - (a, b, c)| < δ, g(x, y, z) = h(x, y, z) = 0일 때마다 f(a, b, c) ≤ f(x, y, z)임
○ 결론 : λ, μ ∈ ℝ가 있어 ∇f(a, b, c) = λ∇g(a, b, c) + μ∇h(a, b, c)
⑶ 여러 개의 등식제약 하에서의 최적화 문제
① 가정 1. 영역 Ω ⊂ ℝn에서 정의된 두 함수 f : Ω → ℝ, G = (g1, ···, gn)' : Ω → ℝm가 주어져 있음 (단, n > m)
② 가정 2. 집합 MG = {x ∈ Ω : G(x) = 0} 위에서 정의된 함수 f|M_G : MG → 이 점 p ∈ MG에서 극대값이나 극소값을 가짐
③ 가정 3. 벡터모임 {∇g1(p), ···, ∇gm(p)}가 선형독립
④ 정리 : 다음 등식을 만족하는 실수 λ1, ···, λm이 존재함
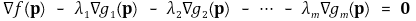
⑤ 증명 : 새로운 함수 ℒ : ℝn+m → ℝ를 도입하여
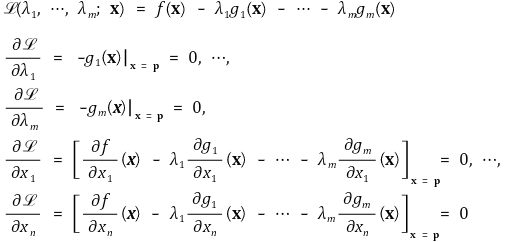
⑷ 극대와 극소를 판정하기 위해서는 다음과 같이 ℒ의 헤세행렬을 구하여 그 부호를 따져봐야 함

① x = p에서 함수 f가 극대값을 가질 충분조건
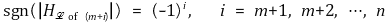
② x = p에서 함수 f가 극소값을 가질 충분조건
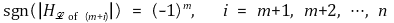
③ 예제 : 원점에서 평면 {(x1, x2, x3)' ∈ ℝ3 : a1 x1 + a2 x2 + a3 x3 + a0 = 1}까지의 거리
○ 극값
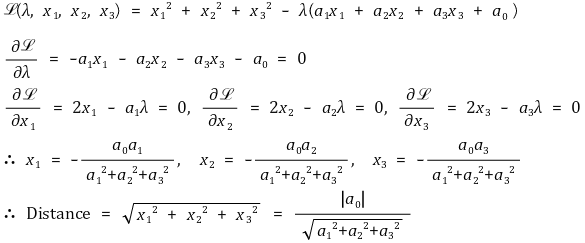
○ 극소값 판정
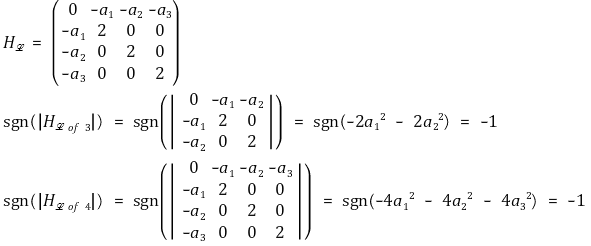
⑸ 포락성 정리(envelop theorem)
⑹ 부등식제약 하에서의 최적화 문제 : 등식제약 하에서의 최적화 문제로 바꾸어서 풂
4. FW 알고리즘(frank-wolfe algorithm) [목차]
⑴ 등식 제약 하 최적화 문제를 푸는 대표적인 알고리즘
⑵ gradient-decent 알고리즘 이전 세대의 알고리즘
입력 : 2020.01.06 19:27
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 12강. 선적분 (0) | 2020.01.10 |
|---|---|
| 【해석학】 10강. 적분 (0) | 2020.01.07 |
| 【해석학】 8강. 미분과 편미분 (0) | 2020.01.01 |
| 【해석학】 7강. 고정점 정리 (1) | 2019.12.26 |
| 【해석학】 6강. 대수학의 기본정리 (0) | 2019.12.26 |




최근댓글