22강. 미분방정식의 해의 안정성
추천글 : 【해석학】 해석학 목차
풀이가 궁금하시면 답변 바랍니다.
1. 선형미분방정식이 유일한 해를 가짐을 증명 [본문]
2. 미분방정식의 해가 초기조건에 연속적으로 의존함을 증명 [본문]
3. 미분방정식을 정의하는 함수에도 해가 연속적으로 의존함을 증명 [본문]
4. 이차 선형미분방정식의 모든 해는 두 개의 해로 생성됨을 증명 [본문]
1. 선형미분방정식이 유일한 해를 가짐을 증명 [목차]
⑴ 예제 : 연속함수 f: (a, b) × ℝn → ℝn가 연속인 편미분

를 갖는다고 하자. 또한 양수 M, L이 있어 모든 a < t < b, x ∈ ℝn, 1 ≤ i, j, ≤ n에 대해 |fi(t, x0)| ≤ M, |∂fi/∂xj(t, x)| ≤ L이 성립한다. 이때 각 (t0, x0) ∈ (a, b) × ℝn에 대해 미분방정식 x(t0) = x0, x'(t) = f(t, x(t))이 유일한 해 x : (a, b) → ℝn를 가짐을 보이시오.
⑵ 예제 : n × n 행렬함수 A(t) = [aij(t)]와 ℝn에서 값을 갖는 벡터함수 f가 (a, b)에서 연속이다. 이때 각 (t0, x0) ∈ (a, b) × ℝn에 대해 미분방정식 x(t0) = x0, x'(t) = A(t)x(t) + f(t)이 유일한 해 x : (a, b) → ℝn를 가짐을 보이시오.
2. 미분방정식의 해가 초기조건에 연속적으로 의존함을 증명 [목차]
⑴ 예제 : 구간 (a, b)에서 연속인 함수 p0(t), ···, pn-1(t), g(t)와 t0 ∈ (a, b), y0, ···, yn-1 ∈ ℝ이 있다. 이때 다음 미분방정식 y(t0) = y0, ···, y(n-1)(t0) = yn-1, p0(t)y(t) + ··· + pn-1(t)y(n-1)(t) + y(n)(t) = g(t)이 유일한 해 y : (a, b) → ℝ를 가짐을 보이시오.
⑵ 예제 : 다음 미분방정식이 유일한 해를 갖는 구간을 한 개만 구하시오.

⑶ 예제 : 다음 미분방정식이 유일한 해를 갖는 구간을 한 개만 구하시오.

⑷ Gronwall 부등식 : 연속함수 u, v : [a, b) → [0, ∞)와 c ≥ 0가 있어 부등식

가 성립한다고 하자. 이때 모든 a ≤ x < b에 대해

를 보이시오.
3. 미분방정식을 정의하는 함수에도 해가 연속적으로 의존함을 증명 [목차]
⑴ 예제 : f(x, y)와
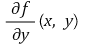
가 V = (a, b) × (c, d) 위에서 연속이다. 또한 (x0, y0) ∈ V와 h, α, δ > 0가 있어 R = [x0 - h, x0 + h] × [y0 - α, y0 + α] ⊆ V이고 δ < α이며 함수 𝜙 : (x0 - h, x0 + h) × (y0 - δ, y0 + δ) → [y0 - α, y0 + α]가 있어 다음 두 조건이 성립한다.
①
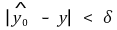
이면
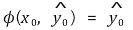
이다.
②
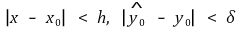
이면
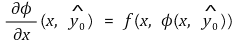
이다. 이때 모든

에 대해 부등식
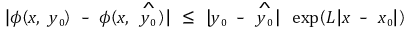
이 성립하는 상수 L ≥ 0이 존재함을 보이시오. 특히 임의의 ϵ > 0에 대해 δ > 0가 있어
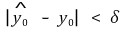
이면
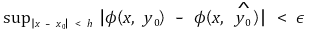
임을 보이시오.
⑵ 예제 : f(x, y), g(x, y)와
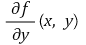
가 V = (a, b) × (c, d) 위에서 연속이다. 또한 (x0, y0) ∈ V와 h, α > 0가 있어 R = [x0 - h, x0 + h] × [y0 - α, y0 + α] ⊆ V이다. 두 함수 𝜙, φ : (x0 - h, x0 + h) → [y0 - α, y0 + α]가 있어 다음 두 조건이 성립한다.
① 𝜙(x0) = y0 = φ(x0)
② |x - x0| < h이면 𝜙'(x) = f(x, 𝜙(x))(x0, y0), φ'(x) = g(x, φ(x))이다. 직사각형 R 위에서
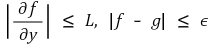
이라 할 때 각 |x - x0| < h에 대해 |𝜙(x) - φ(x)| ≤ ϵheLh임을 보이시오.
⑶ 예제 : 𝜙(x)는 미분방정식 y' = ey, y(0) = 0의 해이고 φ(x)는 미분방정식 y' = 1 + y, y(0) = 0.03의 해라고 하자. 이때 𝜙와 φ는 ℝ 전체에서 정의되고 |x| < 0.06이면 |𝜙(x) - φ(x)| < 0.05임을 보이시오.
4. 이차 선형미분방정식의 모든 해는 두 개의 해로 생성됨을 증명 [목차]
⑴ 예제 : 미분방정식 y" - y' + 2y = 0, y(0) = 1, y'(0) = 3의 해 y : ℝ → ℝ를 구하시오.
⑵ 예제 : a ≠ 0, b, c ∈ ℝ에 대해 미분방정식 ay" + by' + cy = 0의 두 해 y1, y2 : ℝ → ℝ가 있다.
① 다음이 동치임을 보이시오.
○ (s1, s2) ≠ (0, 0)이 있어 s1y1 + s2y2 = 0이다.
○ 모든 t ∈ ℝ에 대해 W(t) ≡ y1(t)y2'(t) - y1'(t)y2(t) = 0이다.
○ τ ∈ ℝ가 있어 W(τ) = 0이다.
② y : ℝ → ℝ가 ay" + by' + cy = 0를 만족하고 s1y1 + s2y2 = 0인 (s1, s2) ≠ (0, 0)이 존재하지 않으면 y = s1y1 + s2y2인 s1, s2 ∈ ℝ이 존재한다.
입력 : 2020.01.18 10:21
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 13강. 미분기하학 (0) | 2020.09.19 |
|---|---|
| 【해석학】 해석학 목차 (0) | 2020.01.18 |
| 【해석학】 21강. 미분방정식의 해의 존재성 (0) | 2020.01.18 |
| 【해석학】 20강. 푸리에 급수 (0) | 2020.01.17 |
| 【해석학】 19강. 무한급수의 수렴판정법 (2) | 2020.01.17 |




최근댓글