13강. 미분기하학(differential geometry)
추천글 : 【해석학】 해석학 목차, 【기하학】 기하학 목차
1. 공간곡선 [본문]
2. 프레네-세레 구조 [본문]
3. 자연방정식 [본문]
a. 벡터와 스칼라
1. 공간곡선 [목차]
⑴ 뒤틀린 입방체(twisted cubic)

⑵ 선직면 : 두 개의 점으로 표현되는 면
2. 프레네-세레 구조 [목차]
⑴ 길이에 대한 매개화

⑵ 단위속력곡선(unit speed curve) : | X'(s) | = 1이므로 X(s)를 단위속력곡선이라고 함
① 공식 1. 벡터 A가 상수크기를 가지고 0이 아니면 A와 dA/dt는 수직

⑶ 단위접벡터장(unit tangent vector field) : T(s)로 표시
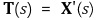
① 접선의 방정식
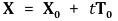
② 법평면 : T를 법선벡터로 하는 평면
⑷ 곡률(curvature) : κ로 표시. || a ||를 벡터 a의 절대값이라고 할 때,

① 곡률반경(radius of curvature) : ρ로 표시
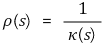
② 공식 1. R = R(t)에 대해 다음 법칙이 성립함
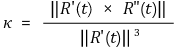
○ 위 공식 증명에서 다음을 보일 때 다소 많은 계산을 요함
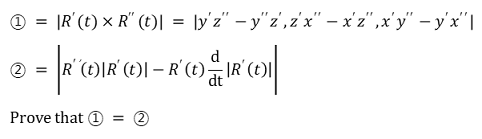
③ 공식 2. E3의 정칙곡선의 곡률은 다음과 같이 주어짐
○ 정칙 곡선 : 도함수가 연속이며 어느 점에서도 동시에 0이 되지 아니하는 곡선
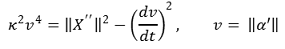
④ 공식 3. 극 방정식으로 주어진 평면곡선 ρ = ρ(θ)에 대해, 곡선의 길이 l 및 곡률은 다음과 같음
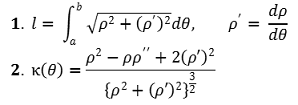
⑤ 공식 4. y = f(x), z = 0을 가지는 xy-평면상의 곡선의 곡률반경은 다음과 같음
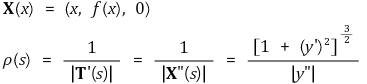
⑥ 공식 5. 기본형식과 곡률
○ 곡면 방정식이 다음과 같이 주어져 있다고 가정
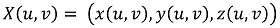
○ 법선 벡터
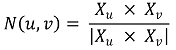
○ 제1 기본형식(1st fundamental form)
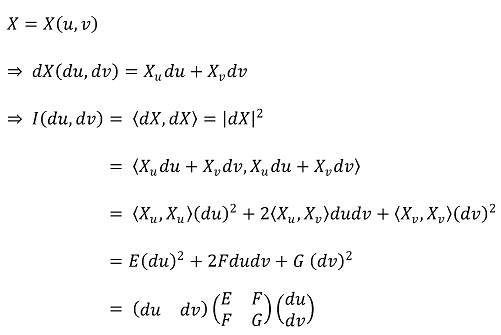
○ 〈ㆍ, ㆍ〉 : 내적
○ X = X(u, v) : 곡면 M을 매개하는 ℝ2 → ℝ3 함수
○ E, F, G : 1st fundamental coefficients
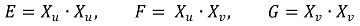
○ 제2 기본형식(2nd fundamental form)
○ 정의 : 어떤 함수 X(u, v): ℝ2 → ℝ3에 대하여, X의 헤세 행렬과 X의 법선 벡터의 내적
○ 수식화
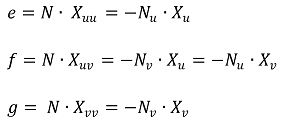
○ 호의 길이
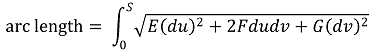
○ 곡면의 면적
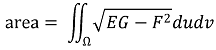
○ 가우스 곡률(Gaussian curvature) K
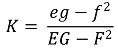
○ 평균 곡률 H
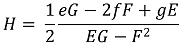
⑸ 주벡터장(principal normal vector field) : N으로 표시. || a ||를 벡터 a의 절대값이라고 할 때,
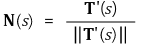
① 주법선의 방정식
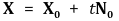
② 전직평면 : N을 법선벡터로 하는 평면
③ 공식 1. 축폐선(evolute) β의 접선은 그 곡선 α : Ⅰ → E2에 수직

⑹ 종법벡터장(binomial vector field) : B로 표시
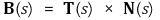
① 종법선의 방정식

② 접촉평면 : B를 법선벡터로 하는 평면
⑺ 열률(torsion) : 〈a, b〉를 벡터 a와 벡터 b의 내적이라고 할 때,
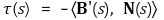
① 공식 1. 다음 식은 수식 전개로 증명할 수 있음
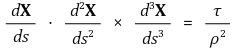
② 공식 2. 평면곡선의 열률은 항상 0 : 공식 1을 통해 쉽게 보일 수 있음
③ 공식 3. 다음은 항상 성립함
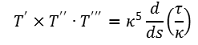
⑻ 프레네-세레 구조(Frenet-Serret structure)
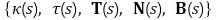
① 공식 1. 다르부 벡터(Darboux vector)
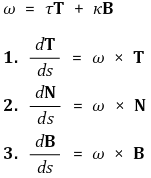
② 예 1. R(t) = (sinh t, cosh t, t)에 대하여,
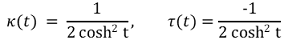
3. 자연방정식 [목차]
⑴ 정의 : 곡선의 식을 결정하기 위한 미분기하학에서의 조건
⑵ 예 1. 직선의 자연방정식 (필요충분조건)
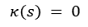
① 정방향 증명 : 직선일 때 κ = 0임은 자명함
② 역방향 증명
○ X'(t)와 X''(t)가 나란하므로 X'(t) // X'(t0)가 성립함
○ X(t) = X(t0) + ∫ X'(t) dt이므로 직선이 성립함
⑶ 예 2. 평면곡선의 자연방정식 (필요충분조건)
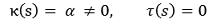
① 조건 1
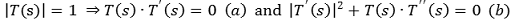
② 조건 2
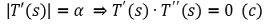
③ 조건 3
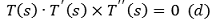
④ T''(s) 식의 표현 : 기저벡터처럼 식을 구성함
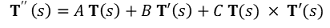
⑤ ⒜, ⒞에 의해 다음을 얻을 수 있음
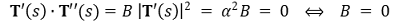
⑥ ⒟에 의해 다음을 얻을 수 있음
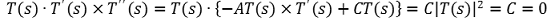
⑦ ⒝에 의해 다음을 얻을 수 있음
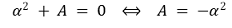
⑧ 중간 결론
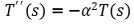
⑨ 최종 결론
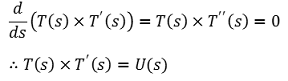
⑷ 예 3. 원의 자연방정식 (필요충분조건)
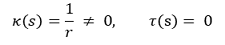
⑸ 예 4. 원주나선의 자연방정식 (필요충분조건)

① 원주나선(circular helix) : 주면나선의 절단면이 원인 경우
② 조건 1
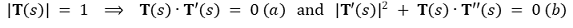
③ 조건 2
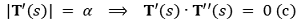
④ 조건 3
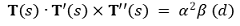
⑤ T''(s) 식의 표현 : 기저벡터처럼 식을 구성함
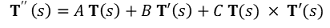
⑥ ⒜, ⒞에 의해 다음을 얻을 수 있음
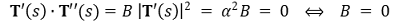
⑦ ⒟에 의해 다음을 얻을 수 있음
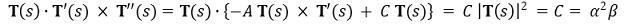
⑧ ⒝에 의해 다음을 얻을 수 있음
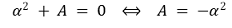
⑨ 중간 결론
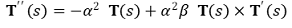
⑩ 최종 결론
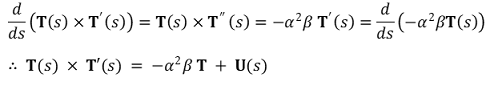
○ T(s) × T '(s)가 T(s)와 수직하므로 양변이 0이 아니면 위 식은 성립하지 않음
○ ∴ -α2β T(s) + U(s) = 0 → T(s)는 상수벡터 → 원주나선의 식을 가짐
○ ∴ T(s) × T '(s) = O
⑸ 예 5. 주면나선의 자연방정식 (필요충분조건)
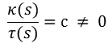
① 주면나선(cylindrical helix, general helix)
○ 나선의 일반적인 형태
○ 즉, 단위접선벡터와 상수단위벡터인 주축이 일정한 경사각을 가짐
⑹ 예 6. 평면곡선 중 다음과 같은 예시가 있을 수 있음
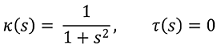
① τ(s) = 0으로부터 평면곡선이고 다음을 만족하는 평면곡선인 것으로 추정됨 (추후 업데이트)
입력: 2020.09.19 19:59
'▶ 자연과학 > ▷ 해석학' 카테고리의 다른 글
| 【해석학】 해석학 문제 및 풀이 (0) | 2022.05.20 |
|---|---|
| 【해석학】 해석학 목차 (0) | 2020.01.18 |
| 【해석학】 22강. 미분방정식의 해의 안정성 (2) | 2020.01.18 |
| 【해석학】 21강. 미분방정식의 해의 존재성 (0) | 2020.01.18 |
| 【해석학】 20강. 푸리에 급수 (0) | 2020.01.17 |




최근댓글