16-2강. 약물 시너지 모델링(synergy in multiple drugs)
추천글 : 【화학】 16강. 반응속도론
1. 개요 [본문]
2. 모델 1. HSA 모델 [본문]
3. 모델 2. Bliss 독립 모델 [본문]
4. 모델 3. Loewe 가산 모델 [본문]
5. 모델 4. ZIP 제로 상호작용 잠재성 모델 [본문]
a. 약리학
b. 약물 라이브러리
c. 약물 클래스 라이브러리
1. 개요 [목차]
⑴ y : 약물의 효과(effect)
① 0 ≤ y ≤ 1
② 일반적으로 세포 사멸률, 세포 억제율 등을 의미
③ 예를 들어, 특정 약제를 쳤을 때 세포 생존율(세포 성장률)이 80%였다면 y = 1 - 0.8 = 0.2라고 할 수 있음
④ 프로그램에서는 y 대신 %inhibition (위 예시에서 20)을 입력으로 넣기도 함
⑵ y1 : 약제 1의 dose x1에서의 효과
⑶ y2 : 약제 2의 dose x2에서의 효과
⑷ yc : 약제 1과 약제 2를 동시에 쳤을 때의 혼합 효과
⑸ yexpected : 약제 1과 약제 2가 상호작용하지 않는다고 가정했을 때 예상되는 효과
⑹ 경우 1. 특정 약제 조합의 한 데이터에서의 시너지즘 판단
① δ = yc - yexpected : delta score. 몇 %를 더 사멸시켰는지
② δ > 0 ⇔ yc > yexpected : 시너지 작용(synergism)
③ δ = 0 ⇔ yc = yexpected : 비상호작용(non-interaction)
④ δ < 0 ⇔ yc < yexpected : 길항작용(antagonism)
⑤ 아래 모델들은 시너지 여부만 알려주고, 약물 조합이 어떻게 반응 곡선을 바꾸는지는 실험을 통해 결정해야 함
⑺ 경우 2. 특정 약제 조합의 전체 데이터에서의 시너지즘 판단 : 즉, 여러 개의 delta score가 있을 때 해석
① 대표값 : 다만, 아래와 같은 산술 평균 이상의 메트릭을 고민할 필요가 있음

② 최대값 : 어떤 조성에서 시너지가 최대인지도 알 수 있음
Δmax = max (δi)
③ 신뢰도 α 양측검정의 신뢰구간

⑻ 요약 : 개인적으로 ZIP 모델이 정답이라고 생각
2. 모델 1. HSA 모델(highest single agent model) [목차]
⑴ Gaddum's non-interaction model이라고도 함
⑵ 가정 1. 상호작용이 없다고 가정했을 때 예상되는 효과 : point estimator
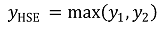
3. 모델 2. Bliss 독립 모델(Bliss independence model) [목차]
⑴ 가정 1. 상호작용이 없다고 가정했을 때 예상되는 효과 : point estimator
① 약물의 효과 y를 어떤 사건의 확률로 생각
② 사건 A, B에 대해 p(A ∪ B) = p(A) + p(B) - p(A ∩ B)가 성립함을 이용하여 식을 구성
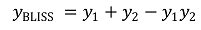
⑵ Bliss 독립 모델과 ZIP 모델
① 실제 drug-response curve (≒ 4PL 함수)를 이용한 ZIP 모델도 Bliss 독립 모델의 한 예시라고 할 수 있음
② ZIP 모델은 각 drug의 일반화 과정을 포함할 뿐 실제 delta score 구할 때 그런 일반화가 필요 없으면 Bliss와 동일한 결론
4. 모델 3. Loewe 가산 모델(Loewe additivity model) [목차]
⑴ CompuSyn, drc (R studio), SYNERGY (R studio) 등이 있음
① CompuSyn : 가장 많이 사용하는 interaction score
⑵ 가정 1. 상호작용이 있어도 각 약제의 dose-response curve가 바뀌지 않음
⑶ 가정 2. 상호작용이 없다고 가정했을 때 예상되는 상황
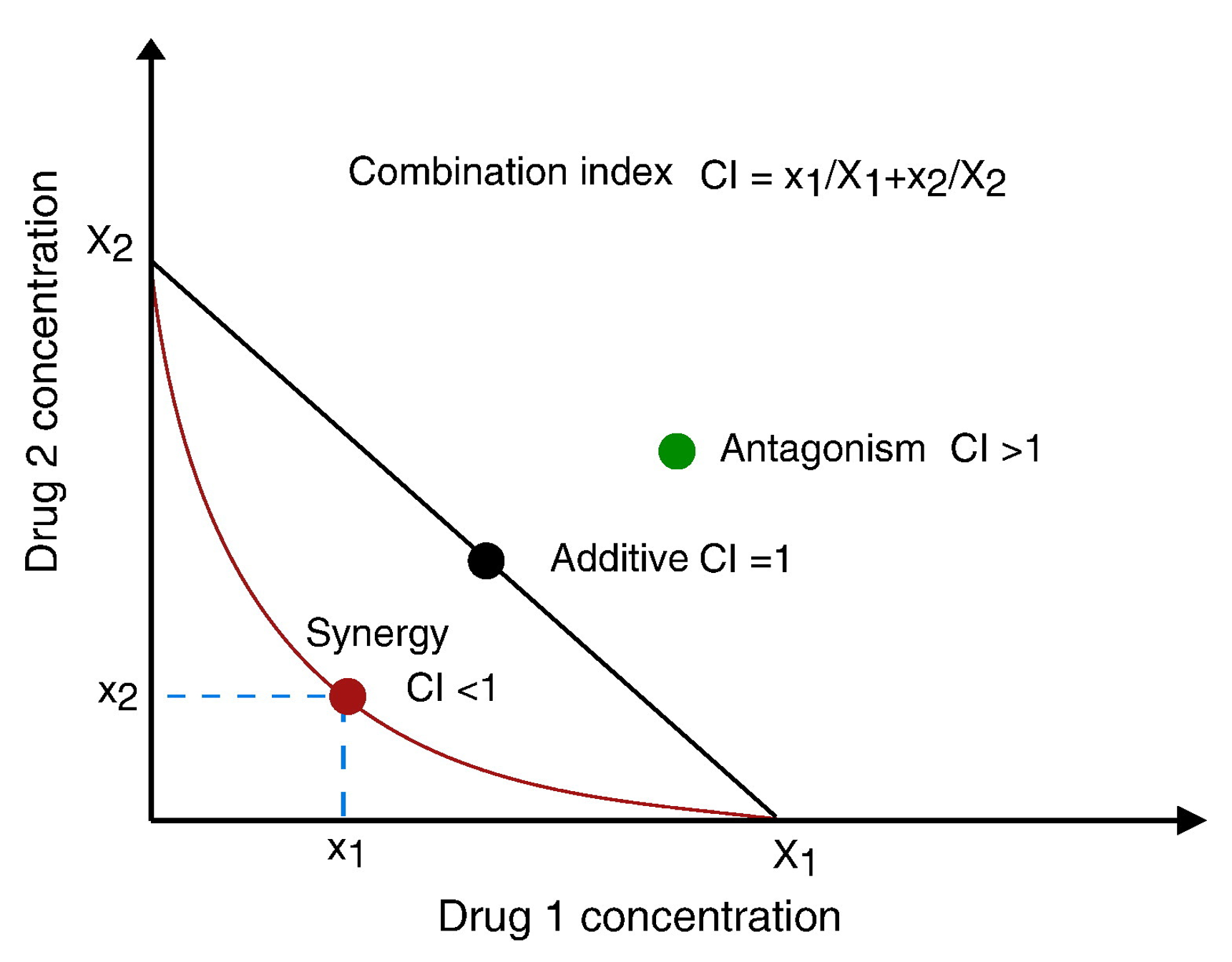
① 상호작용이 없을 때 동일한 효과를 내는 (x1, x2)의 집합은 직선으로 나타남
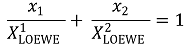
○ 사실상 동일한 약제인 약제 1, 2에 대해 x1를 줄이고 x2를 그만큼 늘릴 때 효과는 당연히 동일
② 혼합 지수(combination index, CI)
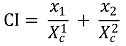
○ Xc1 : yc의 효과를 내기 위해 단독으로 약제 1을 처리할 때 필요한 농도
○ Xc2 : yc의 효과를 내기 위해 단독으로 약제 2를 처리할 때 필요한 농도
③ 예 : 약제 1, 2가 시너지 작용이 있는 경우
○ (x1, x2)이 (Xc1, 0)과 (0, Xc2)를 잇는 직선보다 원점에 가까움
○ 즉, yc의 효과를 내는 데 예상한 농도보다 적은 농도로 동일한 효과를 냈다는 의미
○ 혼합 지수를 이용한 표현
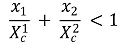
④ 시너지즘 판단 방법
Figure. 1. 시너지즘 판단 방법
⑷ 가정 3. 약물-반응 곡선의 표현 : 4PL(4-parameter log-logistic) 함수를 이용
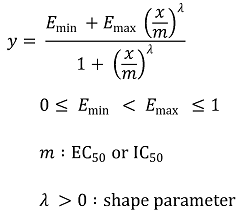
① Chou and Talalay median effect equation
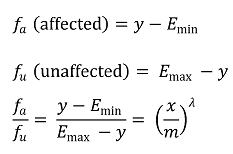
② constant relative potency model
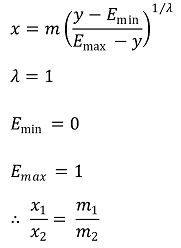
③ 상호작용이 없다고 가정했을 때 예상되는 효과(yLOEWE) : 가정 2 식에 x 대신 yLOEWE에 대한 식을 대입

④ 약제 1과 약제 2가 동일할 때 yLOEWE에 대한 식 : 합리적인 식이 도출됨
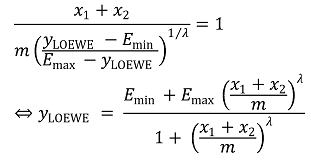
⑸ 때때로 interaction index α를 도입하기도 함 : α = 0일 때 CI = 1, 즉 무상호작용을 나타냄
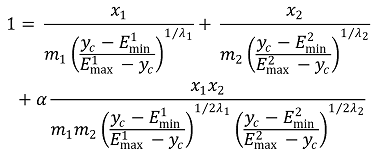
⑹ 단점 : 가정 1 때문에 당연히 문제가 됨
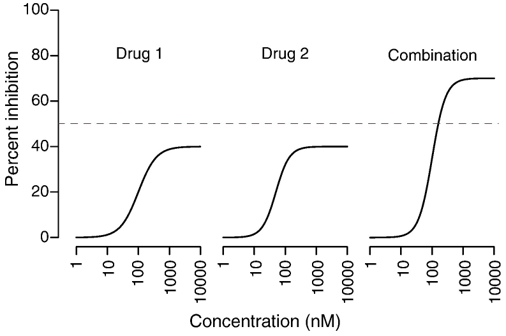
① 예 1. 약물 1을 중심으로 약물 2를 쳤을 때의 결과와 약물 2를 중심으로 약물 1을 쳤을 때의 결과가 다를 수 있음
② 예 2. 각 약물의 달성 가능한 효과보다 더 큰 시너지 효과를 분석할 수 없음
Figure. 2. Loewe 가산 모델의 단점
5. 모델 4. 제로 상호작용 잠재성 모델(zero interaction potency, ZIP) [목차]
⑴ 개요
① 특징 1. 약물-반응 곡선의 표현은 Loewe 가산 모델을 따름
② 특징 2. 상호작용이 없다고 가정했을 때 예상되는 효과는 Bliss 독립 모델을 따름
⑵ 가정 1. 약물-반응 곡선의 표현 : 4PL(4-parameter log-logistic) 함수를 이용. 일단 Emin = 0, Emax = 1로 가정
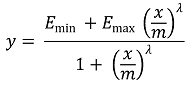
① 상호작용이 없을 때, 약제 1을 중심으로 약제 2를 쳤을 때 예상되는 혼합 효과 : Emin = y2로 증가시킴
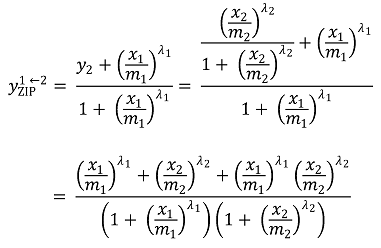
② 상호작용이 없을 때, 약제 2를 중심으로 약제 1을 쳤을 때 예상되는 혼합 효과
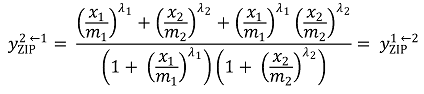
③ yZIP = yZIP1←2 = yZIP2←1은 결국 Bliss 독립 모델과 비슷한 형태가 됨
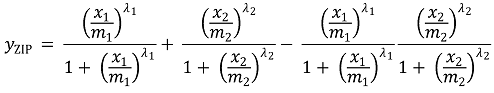
⑶ 가정 2. 상호작용이 있으면 없을 때와 달리 각 약제의 dose-responce curve가 바뀌기 시작함
① 상호작용이 있을 때, 약제 1을 중심으로 약제 2를 쳤을 때 예상되는 혼합 효과
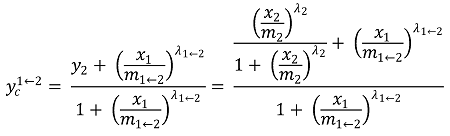
② 상호작용이 있을 때, 약제 2를 중심으로 약제 1을 쳤을 때 예상되는 혼합 효과
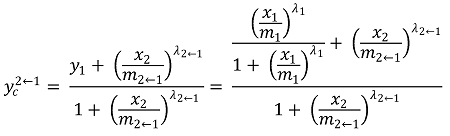
③ delta score : 전체적인 상호작용 잠재성을 평가하기 위해 도입
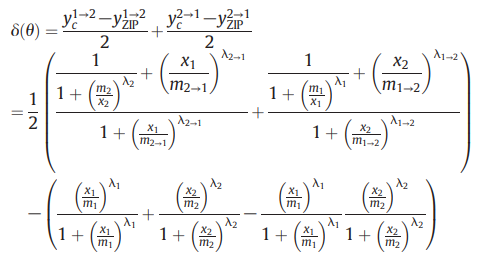
④ 약제 1과 약제 2가 동일할 때, m1 = m2 = m1←2 = m2←1, λ1 = λ2 = λ1←2 = λ2←1이므로 다음이 성립함
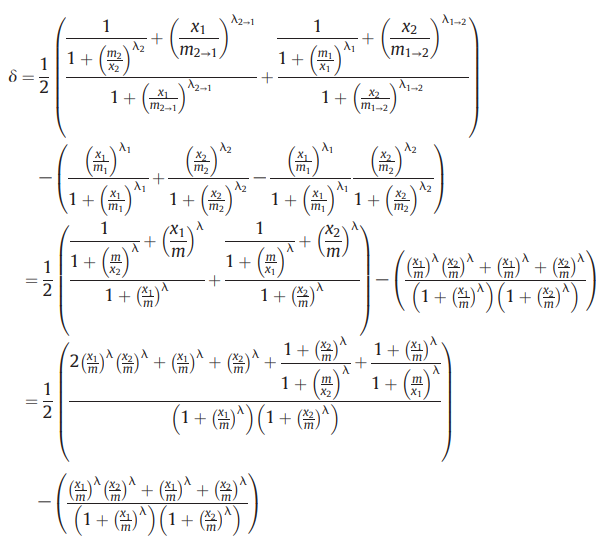
⑤ 다음 식은 자명하게 성립함
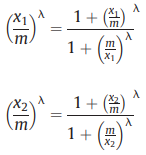
⑥ 약제 1과 약제 2가 동일할 때 δ = 0이 성립함
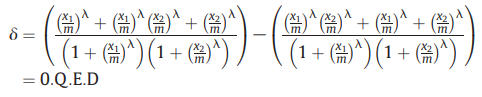
⑦ Emin = 0, Emax = 1이라는 가정이 없을 때 delta score는 다음과 같음
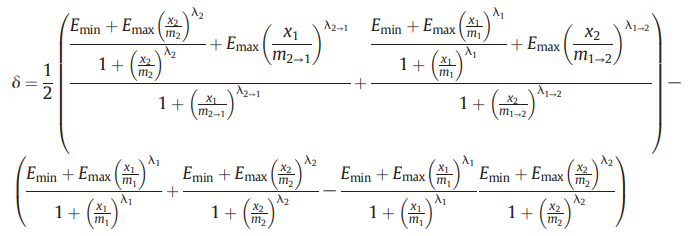
입력 : 2022.10.01 18:10
'▶ 자연과학 > ▷ 일반화학' 카테고리의 다른 글
| 【화학】 화학 목차 (11) | 2024.07.15 |
|---|---|
| 【화학】 24-1강. 화학 실험 예제 (0) | 2024.07.05 |
| 【화학】 24강. 일반화학 실험 (3) | 2022.07.06 |
| 【화학】 16-1강. 약리학(PK/PD) (0) | 2022.04.22 |
| 【화학】 15-2강. 전기화학 반응속도론과 배터리 (2) | 2022.04.21 |



최근댓글