jgex_ag_231 문제 재구성 및 풀이
추천글 : 【머신러닝】 AlphaGeometry 설치 및 이해
1. 문제 재구성 [본문]
2. 풀이 [본문]
3. 부록 [본문]
1. 문제 재구성 [목차]
⑵ 한 예시로서 complete_014_7_Book_00EE_08_E061-66.gex
○ a b = segment a b; c = s_angle b a c 60; d = foot d a b c; e = foot e b a c; g = circumcenter g b c a; f = on_line f a d, on_line f b e ? cong a f a g
⑶ 문법 검토
① a b = segment a b : 선분 AB가 주어져 있다
② c = s_angle b a c 60 : ∠BAC = 60°이다
③ d = foot d a b c : D는 A에서 BC 위로 수직선을 그었을 때의 교점이다
④ e = foot e b a c : E는 B에서 AC 위로 수직선을 그었을 때의 교점이다
⑤ g = circumcenter g b c a : G는 △BCA의 외심이다
⑥ f = on_line f a d, on_line f b e : F는 선분 AD와 BE의 교점이다
⑦ ? cong a f a g : AF = AG임을 증명하여라
⑷ 문제 재구성
선분 AB가 주어져 있으며, ∠BAC = 60°이다. 점 D는 A에서 BC 위로 내린 수선의 발이며, 점 E는 B에서 AC 위로 내린 수선의 발이다. 점 G는 삼각형 BCA의 외심이고, 점 F는 선분 AD와 BE의 교점이다. 이때 AF = AG임을 증명하여라.
Given a line segment AB, with ∠BAC = 60°. Let D be the foot of the perpendicular from A to BC, and E be the foot of the perpendicular from B to AC. Let G be the circumcenter of triangle BCA, and F be the intersection of lines AD and BE. Prove that AF = AG.
2. 풀이 [목차]
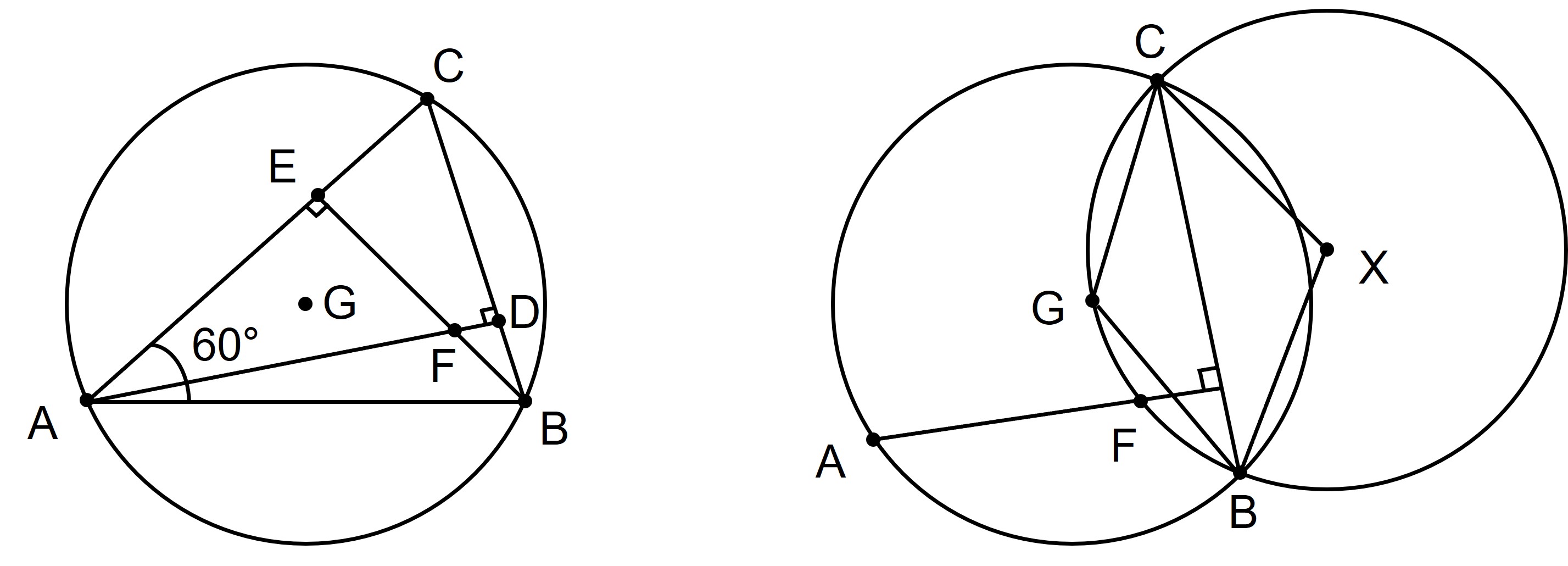
○ ∠BGC = 2 × ∠BAC = 120°
○ ∠FCD + ∠FBD = ∠CFE = ∠CAB = 60°이므로 ∠BFC = 180° - 60° = 120°
○ 따라서 B, C, F, G는 cyclic
○ X는 △BCG의 외심
○ 내접사각형의 마주보는 각의 합은 180°이므로 ∠BXC = 2 × (180° - 120°) = 120°
○ 따라서 외접원 G와 외접원 X는 동일한 반지름을 가짐
○ 그러므로 XC = XB = XG = GX = GC = GB
○ 이를 통해 두 이등변 삼각형이 BC를 공통으로 붙어 있으므로 GX는 BC와 수직함
○ 그러므로 AF ⊥ BC로부터 GX // AF를 얻을 수 있음
○ △XFG와 △AGF에 대하여 XF = XG = AG, ∠XFG = ∠AGF (∵ GX // AF), GF는 공통이므로 △XFG ≡ △AGF
○ 따라서 XF = XG이듯이 AG = AF가 성립함
3. 부록 [목차]
○ jgex_ag_231 기하 문제 풀이 [01-20]
○ jgex_ag_231 기하 문제 풀이 [21-40]
○ jgex_ag_231 기하 문제 풀이 [41-60]
○ jgex_ag_231 기하 문제 풀이 [61-80]
○ jgex_ag_231 기하 문제 풀이 [81-100]
○ jgex_ag_231 기하 문제 풀이 [101-120]
○ jgex_ag_231 기하 문제 풀이 [121-140]
○ jgex_ag_231 기하 문제 풀이 [141-160]
○ jgex_ag_231 기하 문제 풀이 [161-180]
○ jgex_ag_231 기하 문제 풀이 [181-200]
○ jgex_ag_231 기하 문제 풀이 [201-220]
○ jgex_ag_231 기하 문제 풀이 [221-231]
입력: 2024.08.01 10:16
'▶ 자연과학 > ▷ 기하학' 카테고리의 다른 글
| 【AlphaGeometry】 jgex_ag_231 기하 문제 풀이 [21-40] (0) | 2024.08.07 |
|---|---|
| 【AlphaGeometry】 jgex_ag_231 기하 문제 풀이 [01-20] (0) | 2024.08.07 |
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2020년 ~ 2024년) (0) | 2024.05.05 |
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2015년 ~ 2019년) (0) | 2024.05.05 |
| 【국제수학올림피아드】 IMO 기하 문제 풀이 (2010년 ~ 2014년) (2) | 2024.05.05 |


최근댓글