제 33회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 33회 전국 대학생 수학 경시대회
제 2 분야
2014년 11월 15일 (10:00 - 13:00)
1. 양의 정수 n과 함수 f(x) = ex / (x - 1)에 대하여 f(n)(x) = Pn(x) ex / (x - 1)n+1을 만족하도록 다항식 Pn(x)를 정의하자. 이때, Pn(1)과 Pn'(1)을 구하여라.
Solution.

2. 모든 항이 실수인 수열 { an }과 { bn }은 다음을 만족한다. 수열 { an }이 수렴함을 보여라.

Solution.

3. 양의 정수 m에 대하여 Am = O을 만족하는 임의의 n × n 실행렬 A는 다음을 만족함을 보여라. (단, O는 영행렬)
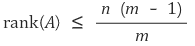
Solution.

4. 다음 적분값을 구하여라.
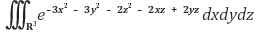
Solution.

5. 양의 정수 n (n ≥ 2)에 대하여 n × n 실행렬로 이루어진 실벡터 공간을 Mn(ℝ)이라 하자. 다음의 조건을 모두 만족하는 부분집합 V는 dim(V) = dim(Mn(ℝ))임을 보여라. (단, Eij는 i행과 j열이 만나는 항만 1이고 나머지는 모두 0인 행렬).
(ⅰ) V는 Mn(ℝ)의 부분공간이다.
(ⅱ) A, B ∈ V이면 AB ∈ V이다.
(ⅲ) E12 + E23 + … + En-1, n ∈ V이고 E21 + E32 + … + En, n-1 ∈ V.
Solution.

6. 함수 f : ℝ → ℝ은 두 번 미분가능하고 f(0) = 0을 만족한다. 다음 부등식을 증명하여라.
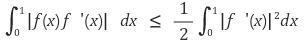
Solution.

7. 실행렬 A, B는 고유치가 모두 양수인 n × n 대칭행렬이다. 임의의 n × n 실행렬 C에 대하여 2n × 2n 행렬
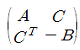
는 역행렬을 가짐을 보여라 (단, CT는 C의 전치행렬).
Solution.

8. f : [a, b] → ℝ가 [a, b]에서 연속이고, 임의의 0 ≤ t ≤ 1와 a ≤ x, y ≤ b에 대하여, f(tx + (1 - t)y) ≤ tf(x) + (1 - t)f(y)를 만족한다 (단, a < b). 다음 부등식을 증명하여라.
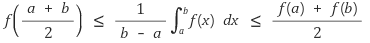
Solution.
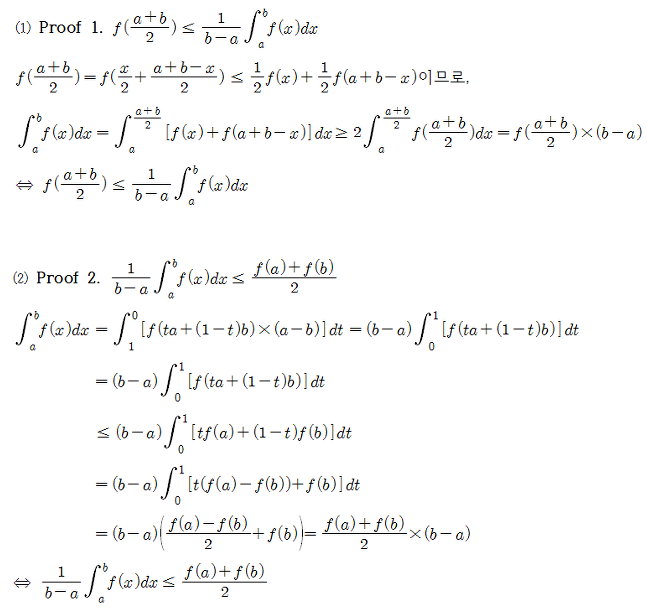
입력: 2015.08.26 11:43
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 31회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.25 |
|---|---|
| 【대수경】 제 31회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.25 |
| 【대수경】 제 32회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.25 |
| 【대수경】 제 32회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.25 |
| 【대수경】 제 33회 전국 대학생 수학 경시대회 제 1 분야 (3) | 2016.06.25 |




최근댓글