제 27회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 27회 전국 대학생 수학 경시대회
제 1 분야
2008년 11월 15일 (10:00 - 13:00)
1-1. 꼭짓점의 좌표가 (0, 1, 0), (1, 2, 1), (1, 3, 3), (3, 2, 1)인 사면체의 부피를 구하여라.
Solution.
① 벡터 x = (1, 2, 1) - (0, 1, 0) = (1, 1, 1),
② 벡터 y = (1, 3, 3) - (0, 1, 0) = (1, 2, 3),
③ 벡터 z = (3, 2, 1) - (0, 1, 0) = (3, 1, 1).

1-2. 0 < a, b, c, d < 1일 때, 다음 부등식이 성립함을 보여라.
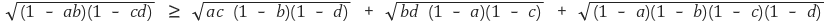
Solution.

1-3. 다음 적분을 계산하여라.
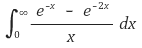
Solution.
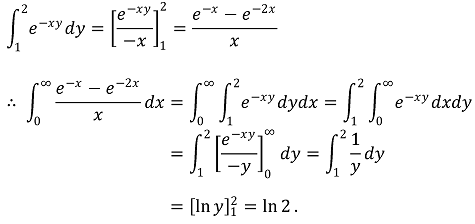
1-4. α > 1일 때, 다음 적분 값이 존재함을 보여라.

Solution.
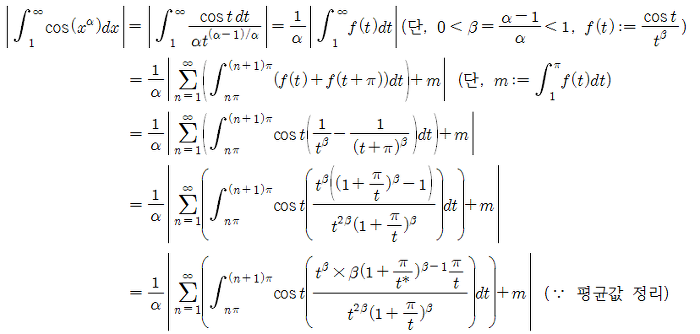

1-5. 다음 값을 구하여라.
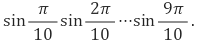
Solution.
우선 θ = π / 5에 대하여, 다음을 보이자.
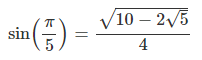
⑴ sin 3θ = sin (3π / 5) = 3 sin θ - 4 sin3 θ
⑵ sin 2θ = sin (2π / 5) = 2 sin θ cos θ
⑶ sin 3θ = sin(π - 3θ) = sin 2θ이므로,
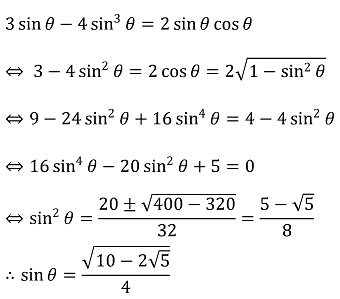
따라서 (준식)은 다음과 같다.
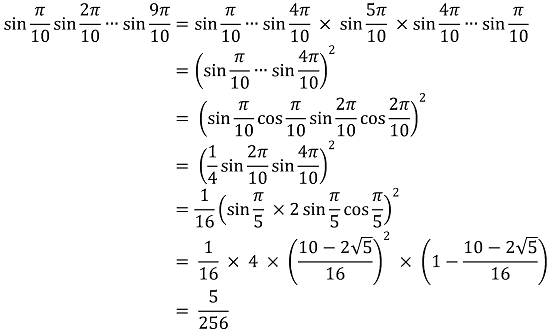
2-1. 모든 성분이 양수인 3 × 3 행렬 A의 역행렬 A-1이 존재한다. A-1의 성분 중에서 양수인 성분이 6개일 때, A-1의 성분 중에서 음수인 성분은 3개임을 보여라.
Solution.
우선 A-1의 세 열벡터 중 하나가 모두 양수인 성분으로 이루어졌다고 생각하자.
이때 그 열벡터와 A의 세 행벡터 중 하나의 내적이 단위행렬 I의 대각선 성분(=1)이 된다.
따라서 나머지 두 행벡터의 내적은 0이 되는데 성분이 모두 양수이므로 이는 모순이다.
따라서 A-1의 세 열벡터는 모두 하나 이상의 양수가 아닌 성분으로 이루어져 있다.
A-1의 성분 중에서 양수인 성분이 6개이므로 세 열벡터는 그러한 값을 단 1개씩 갖는다.
그런데 A-1의 세 열벡터 중 하나가 2개의 양수와 0으로 이루어져 있는 경우를 생각해 보자.
위와 같이 A의 세 행벡터 중 하나의 내적이 단위행렬 I의 대각선 성분(=1)이 된다.
따라서 나머지 두 행벡터의 내적은 0이 되는데 그 내적 값이 양수이므로 이는 모순이다.
따라서 A-1의 세 열벡터는 모두 2개의 양수인 성분과 1개의 음수인 성분을 갖는다.
2-2. 폐구간 [0, 1]에서 정의된 함수열 ϕn이 다음을 만족시킨다.
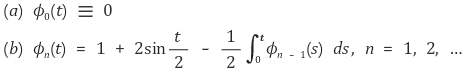
폐구간 [0, 1]에서 함수열 lim ϕn = ϕ이고 ϕ는 미분가능한 함수일 때, 함수 ϕ(t)를 구하여라.
Solution.
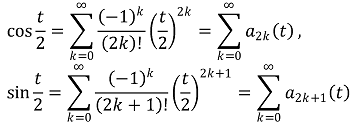
인 { an(t) } n≥0을 정의하자. (단, an(t)는 n차 다항식이다.) 이때 다음을 얻는다.
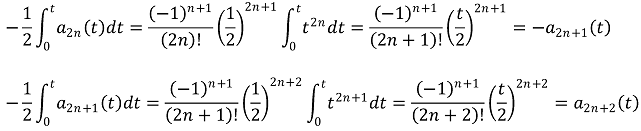
추가로 다음을 확인하자.
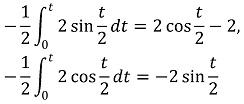
따라서 다음을 귀납적으로 보일 수 있다.

그런데,
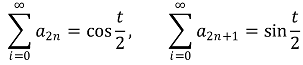
이므로,
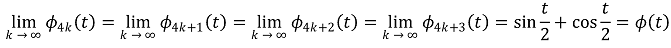
임을 얻는다.
2-3. 모든 n = 0, 1, 2, 3, …에 대해서 an은 0 또는 1이고, P와 Q는 다항식으로서 P의 차수가 Q의 차수보다 낮으며 | x | < 1인 영역에서 다음이 성립한다.
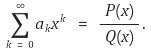
이때, 적당한 자연수 p가 존재하여 모든 n ≥ 0에 대해서 an+p = an이 성립함을 보여라.
Solution.
Q(x) = q0 + q1x + ··· + qnxn, P(x) = p0 + p1x + ··· + pmxm라고 두자.
또한, v = (qn, qn-1, ···, q0), wt = (at-m-1, ···, at)라고 하자. (단, a(-m-1) = ··· = a(-1) = 0)
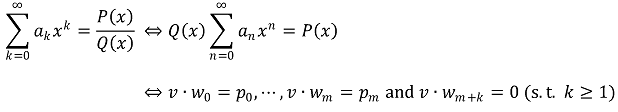
Q(x)와 P(x), 그리고 a0, ···, am을 알고 있고, am+1을 구하는 경우를 생각하자.
이때 am+1의 존재성은 명백하므로 일차방정식 v·wm+1 = 0에서 am+1의 해를 결정 가능.
이러한 논의를 계속하면 {ak} k≥0가 유일하게 결정된다.
그런데 wt의 n+1개의 원소는 0 또는 1이므로 기껏해야 2n+1 가지밖에 없다.
따라서 w0 = wN인 N > m이 존재한다.
wk' = wk+N, k ≥ 0일 때 위의 논의를 그대로 적용하면 {ak} k≥0 = {ak'} k≥0 = {ak} k≥N이다.
2-4. pi, qi > 0이고 p1 + … + pn = q1 + … + qn = 1일 때, 다음 부등식이 성립함을 보여라.
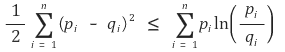
Solution.
pi ≥ 0, qi > 0이고 p1 + ··· + pn = q1 + ··· + qn = 1일 때 주어진 부등식이 성립함을 보이면 충분하다. 단,
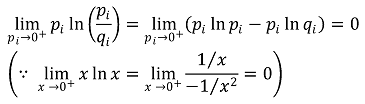
이므로
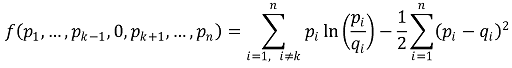
으로 정의하자. 또한 다음과 같이 추가로 정의하자.

이제 닫힌집합이고 유계인 D := { (p1, ..., pn) | g(p1, ..., pn) = 1, pi ≥ 0 }을 생각하자.
f가 연속이므로 f |D는 최댓값과 최솟값을 갖는다. (∵ 최대·최소 정리)
f |D의 최솟값은 D 상의 극값이거나 D의 경계 (⇔ pi = 0인 i가 존재)의 함숫값이다.
⑴ D 상의 극값 : 라그랑주 승수법을 쓰자.
Dif = lnpi - lnqi + 1 - (pi - qi) = λDig = λ인 λ ∈ ℝ가 존재한다. (∵ ∇g ≠ O)
그런데 어떤 i1 ∈ {1, ..., n}에 대해 pi1 > qi1라면 pi2 < qi2인 i2 ∈ {1, ..., n}가 존재한다.
λ - 1 = lnpi1 - lnqi1 - (pi1 - qi1) = (pi1 - qi1)(1/c - 1) > 0 (단, pi1 > c > qi1)
λ - 1 = lnpi2 - lnqi2 - (qi2 - pi2) = (qi2 - pi2)(1 - 1/c') < 0 (단, pi2 < c < qi2)
따라서 모순 ⇔ 극값이 되는 { pi }는 ∀i ∈ {1, ..., n}에 대해 pi = qi가 성립.
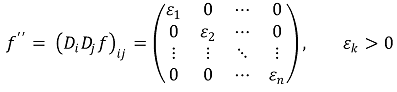
이므로 임의의 방향벡터 v에 대해 Dv2f > 0이다.
따라서 이 경우 함숫값 f(p1, ..., pn) = 0은 극솟값이다.
⑵ D의 경계 (⇔ pi = 0인 i가 존재)
위의 논의를 적용하자.
D의 내부에 있는 모든 점의 경우 f '' > 0이므로 아래로 볼록이다.
즉, λ1 + λ2 = 1, λ1, λ2 ≥ 0과 임의의 두 점 P1, P2 ∈ (D의 내부)에 대해
f(λ1P1 + λ2P2) ≤ λ1f(P1) + λ2f(P2) (※)가 성립한다. (∵ g(t) = P1 + t(P2 - P1)을 고려)
f(p1, ..., pn)은 D 상에서 연속이므로 (※)가 D 전체의 점에서도 성립한다.
경계상의 점 P*에 대해, 함숫값 f(P*)이 최솟값이 된다고 가정하자.
그러면
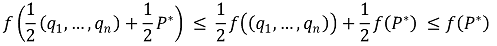
이므로 (q1, ..., qn) 외에 극점이 더 존재하고 이는 ⑴의 결론과 모순된다.
따라서 그러한 점 P*가 존재하지 않는다.
그러므로 f(p1, ..., pn) ≥ f(q1, ..., qn) = 0 ⇔ 주어진 부등식은 참이다.
2-5. 수열 { xn }이 다음 조건
xm > 0, xm+n ≤ xm + xn, m,n = 1, 2, 3, …
을 만족할 때, 수열 { xn/n }이 수렴함을 보여라.
Solution.

입력: 2015.10.18 19:56
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 제 26회 전국 대학생 수학 경시대회 제 1 분야 #01-01 (0) | 2016.06.26 |
|---|---|
| 【대수경】 제 27회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.26 |
| 【대수경】 제 28회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.26 |
| 제 28회 전국 대학생 수학 경시대회 제 1 분야 #08 (0) | 2016.06.26 |
| 【대수경】 제 28회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.26 |




최근댓글