제 27회 전국 대학생 수학 경시대회 제 2 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 27회 전국 대학생 (공업)수학 경시대회
제 2 분야
2008년 11월 15일 (10:00 - 13:00)
1-1. 꼭짓점의 좌표가 (0, 1, 0), (1, 2, 1), (1, 3, 3), (3, 1, 2)인 사면체의 부피를 구하여라.
Solution.
① 벡터 x = (1, 2, 1) - (0, 1, 0) = (1, 1, 1),
② 벡터 y = (1, 3, 3) - (0, 1, 0) = (1, 2, 3),
③ 벡터 z = (3, 1, 2) - (0, 1, 0) = (3, 0, 2).

1-2. 다음 적분을 계산하여라.

Solution.

1-3. 다음 적분을 계산하여라.

Solution.

1-4. α > 1일 때, 다음 적분값이 존재함을 보여라.

Solution.

1-5. 다음을 만족시키는 행렬 A를 하나만 구하여라.
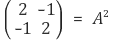
Solution.
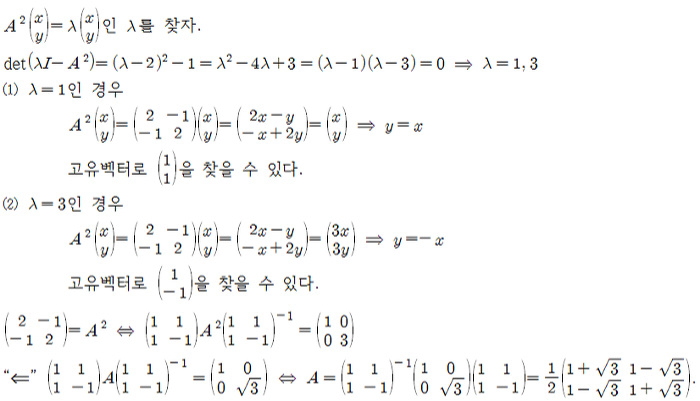
1-6. 다음을 만족시키는 함수 f(x, y, z)를 구하여라.
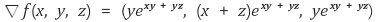
Solution.

1-7. 집합 {(x, y) | x2 + y2 = 1}에서 함수 f(x, y) = 3x2 + 4xy + y2의 최댓값을 구하여라.
Solution.

1-8. 다음을 만족시키는 3 × 1 행렬 u와 v를 모두 구하여라.

Solution.

2-1. n × n 행렬 A = { aij }의 원소가 임의의 j = 1, 2, …, n에 대하여 a1j + … + anj = 0을 만족할 때, A의 역행렬은 존재하지 않음을 보여라.
Solution.

2-2. 폐구간 [0, 1]에서 정의된 함수열 ϕn이 다음을 만족시킨다.
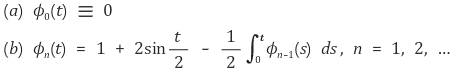
폐구간 [0, 1]에서 ϕn의 극한 ϕ가 미분가능한 함수일 때, 함수 ϕ(t)를 구하여라.
Solution.

2-3. 다음 조건을 모두 만족시키는 다항함수 u(x, y)를 모두 구하여라.
⒜ uxx + uyy = 0.
⒝ 모든 실수 x에 대하여 u(x, 0) = u(x, √3 x) = 0.
⒞ 모든 x > 0, 0 < y < √3 x에 대하여 u(x, y) > 0.
⒟ 모든 실수 t에 대하여 u(tx, ty) = tnu(x, y)를 만족시키는 양의 정수 n이 존재.
Solution.

2-4. 모든 n = 0, 1, 2, 3, …에 대해서 an은 0 또는 1이고, P와 Q는 다항식으로서 P의 차수가 Q의 차수보다 낮으며 | x | < 1인 영역에서 다음이 성립한다.
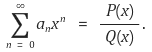
이때, 적당한 자연수 p가 존재하여 모든 n ≥ 0에 대하여 an+p = an이 성립함을 보여라.
Solution.

2-5. 다음에 주어진 4개의 자료 (xi, yi), i = 1, 2, 3, 4에 대하여 오차의 제곱의 합을 가장 작게 만드는 직선 y = ax + b를 구하여라.
(0, 0), (1, 1), (3, 2), (4, 5)
즉, 다음 값
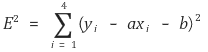
을 가장 작게 만드는 직선 y = ax + b를 구하여라.
Solution.

입력: 2015.10.24 22:09
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 제 26회 전국 대학생 수학 경시대회 제 1 분야 #01-02 (0) | 2016.06.26 |
|---|---|
| 제 26회 전국 대학생 수학 경시대회 제 1 분야 #01-01 (0) | 2016.06.26 |
| 【대수경】 제 27회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.26 |
| 【대수경】 제 28회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.26 |
| 제 28회 전국 대학생 수학 경시대회 제 1 분야 #08 (0) | 2016.06.26 |




최근댓글