2-1강. 전기장에 대한 가우스 법칙 증명
추천글 : 【전자기학】 2강. 맥스웰 제1법칙
Q.
Maxwell's equations 중 하나인 '전기장에 대한 가우스(Gauss) 법칙'은 다음과 같이 기술하고 있다.

이때 주어진 환적분은 임의의 폐곡면 S에 대해서 면적분을 하라는 의미이다. 이제 이 식을 증명해 보자.
Solution.
이 식을 증명하기 위해서는 발산정리의 증명이 선행될 필요가 있다. 발산 정리는 다음 내용을 기술한다.

다음과 같은 임의의 직육면체를 설정하고 이 정리가 정말 성립하는지 확인해 보자.

그럼 삼중적분은 다음과 같다.

이때 중복되는 표현을 줄이기 위해 cyc 형태로 계산을 단순화 했다. 어쨌든 이렇게 임의의 직육면체에 대해 발산 정리가 성립함을 보였는데, 이를 귀납적으로 적용하면 임의의 영역과 그 경계에 대해서도 증명해 볼 수 있다.
두 개의 직육면체를 아무렇게나 이어붙인 영역에 대해서도 면이 겹치는 부분은 서로 상쇄되므로(∵ 법선벡터가 서로 반대방향을 향함) 여전히 해당 정리는 유효하다. 그런데, 이런 식으로 직육면체를 적절히 조합하면 임의의 '각진 입체도형'에 대해서도 증명할 수 있다. 그런데 곡면은 그러한 '각진 입체도형'의 극한으로 표현할 수 있으므로 임의의 영역과 그 경계에 대해서 귀납법을 통해 증명한 셈이다. (단, 적분값의 존재성[수렴성]은 적절한 상계 및 하계를 잡을 수 있음에서 쉽게 증명된다. 확인해 봐라!)
따라서 발산정리는 증명됐다. 그런데, 전기장 벡터와 같은 거리의 제곱에 반비례하는 벡터는 발산량이 항상 0임이 잘 알려져 있다. 따라서 발산 정리에 의해 임의의 폐곡면에 대한 면적분은 항상 0이어야 할 것 같다는 추론을 해볼 수 있다.
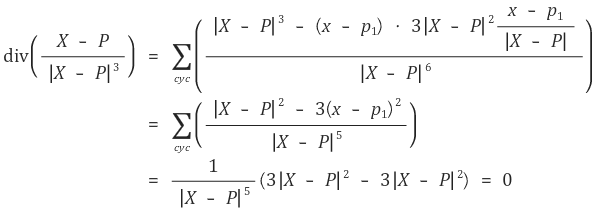
그런데 이러한 전기장 벡터를 가지고 발산정리를 정의하기 까다로운 점이, 전하를 둘러싼 영역에 대해 3중 적분을 시도하는 경우 그 전하와 가까워질수록 전기장의 크기가 발산한다는 점이다. 따라서 앞서 0일 것 같다는 예상과 달리 그러한 영역의 적분은 특정 값을 가지게 된다.
그 구체적인 값을 구하기 위해 해당 전하 주위로 반지름이 δ ≪ 1인 어떤 구(V'; S')를 고려해 볼 수 있다.

그러면 이제 발산정리를 적용하는데 어떤 문제도 없다. 따라서
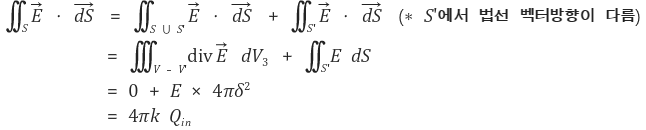
이때 최종항이 Qin / ε0가 되도록 ε0을 정의한다. 따라서 전기장에 대한 가우스 법칙을 증명하였다. 실은 마지막에는 쿨롱 법칙을 이용하였다. 다만, 이 법칙이 의미를 가지는 이유는 단순히 방사상의 전기장에 대한 공식보다 더 본질적이고, 더 유용하기 때문이다.
입력: 2015.12.05 00:15
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【전자기학】 호흡정지감지기 (0) | 2019.03.18 |
|---|---|
| 【물리학】 도르래를 타면서 힘을 주는 사람은 힘의 이득이 2이다. (3) | 2016.10.20 |
| 【물리학】 역학 3-1강. 코리올리 힘 (0) | 2016.06.27 |
| 【물리학】 역학 6-1강. 회전하는 물체에서의 오일러 방정식 유도 (0) | 2016.06.27 |
| 【물리학】 역학 5-1강. 로켓방정식 (0) | 2016.06.27 |




최근댓글