역학 3-1강. 코리올리 힘
추천글 : 【물리학】 역학 3강. 운동의 법칙
Q.
북반구에서 발달한 태풍의 경우 북상하면서 오른쪽으로 방향이 꺾인다. 이는 지구가 자전하기 때문에 생기는 가상의 힘 때문이다. 이 힘을 전향력 또는 코리올리 힘(coriolis force)이라고 한다. 북반구에서는 움직이는 물체의 이동방향에 대해 오른쪽으로 수직하고, 남반구에서는 움직이는 물체의 이동방향에 대해 왼쪽으로 수직하다.

이 힘은 지구대순환을 일으키는 장본인이기도 하다. 잘 알다시피 적도는 높은 온도로 인해 적도저압대가 형성돼 있고, 극에서는 낮은 온도로 인해 극고압대가 형성돼 있다. 이로 인해 적도에서 위도 30도까지는 지표기준 적도로 향하는 기류가 형성되고, 위도 60도부터 극까지는 지표기준 극에서 위도 60도로 향하는 기류가 형성돼 있다. 위도 30도에서 60도까지는 뚜렷한 순환 동력이 없어서 위 아래 기류흐름을 보상하기 위해 기류가 형성되며 이 방향은 극 방향을 향한다. (실제로 이 구간에서의 기류 흐름은 불명확하다.)

이렇듯 지구상의 다양한 현상을 해석하기 위해서는 코리올리 힘에 대한 이해가 분명해야 할 필요가 있다. 이를 증명해 보자. 코리올리 힘은 다음과 같이 공식화된다고 한다.
Solution.
전향력을 일으키는 물체들은 모두 떠 있는 물체들이다. 따라서 태풍이나 기류와 같은 대상이 전향력을 받게 되는 것이다. 떠 있으면 지표의 수직항력으로부터 비교적 자유롭게 되고, 이로써 지구상의 다른 물체들이 동일하게 회전을 할 때 그 물체들은 가만히 있을 수 있다. 물체들이 어떤 고정된 좌표계를 기준으로 운동성분이 있다고 하면 다음과 같이 표현할 수 있다.
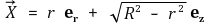
이때 er은 지구의 자전축에 수직한 적도면의 방사상의 단위벡터이고, ez는 자전축에 나란한 단위벡터이다. 이때 물체가 지구의 중력에 의해 지구 표면에 붙들어져 있음을 반영하였다.
그런데 실제 관찰자는 ω의 각속도로 자전을 한다. 따라서 위 벡터표현을 관찰자 기준으로 변형할 필요가 있다. 어떤 카메라멘이 각가속도 ω로 회전하면서 촬영을 할 때, 영상에 담긴 물체는 두 가지 현상이 관찰된다.
(1) 원심력이라는 가상의 힘이 관찰된다. (가속도계)
(2) θ → θ - ωt (관찰자의 회전으로 물체의 실제 회전각보다 작게 보인다.)
따라서 물체의 가속도벡터는 다음과 같이 표현된다.
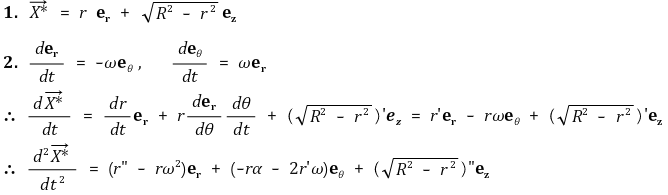
이때 새로 추가된 eθ는 자전축에 수직한 적도면 상의 물체 운동에 대한 접선 단위벡터이다. 이때 er = cos ωt로 표현한다면 eθ = sin ωt가 될 수 있도록 적절하게 정의할 수 있다. 한편, 방사방향의 반지름 자체에 의한 가속도, 접선방향의 각가속도, 자전축 방향의 가속도를 제외하고 유독 눈에 띄는 항이 있다. 바로 -2r'ω eθ 항이다. 이것이 바로 코리올리 가속도가 되겠다. 한편, -rα eθ에 대응하는 항은 접선방향의 가속운동에 대한 관성가속도를 표현하는 항이다.
실제로 문제를 푸는 과정에서 일일히 (r, θ, z)를 정의한 뒤 식을 쓰는 것은 굉장히 귀찮은 일이다. 따라서 코리올리 가속도를 계산하는 보다 직관적인 연산인 외적을 활용하는 것이 바람직하다.
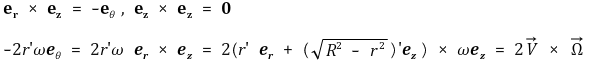
참고로 위에서 ez × ez = 0임을 이용하였다. 따라서 증명은 완료되었다.
입력: 2019.09.26 18:06
수정: 2023.12.10 12:25
'▶ 자연과학 > ▷ 일반물리학' 카테고리의 다른 글
| 【물리학】 도르래를 타면서 힘을 주는 사람은 힘의 이득이 2이다. (3) | 2016.10.20 |
|---|---|
| 【전자기학】 2-1강. 전기장에 대한 가우스 법칙 증명 (0) | 2016.06.27 |
| 【물리학】 역학 6-1강. 회전하는 물체에서의 오일러 방정식 유도 (0) | 2016.06.27 |
| 【물리학】 역학 5-1강. 로켓방정식 (0) | 2016.06.27 |
| 【물리학】 현대물리학 1강. 양자역학 (0) | 2016.06.26 |




최근댓글