RCTD의 이해 및 실행 (ref)
추천글 : 【생물정보학】 생물정보학 분석 목차
1. 개요 [본문]
2. 수학적 이론 [본문]
3. 코드 [본문]
4. 결과 [본문]
5. 결론 [본문]
1. 개요 [목차]
⑴ 기존 spatial transcriptomics의 한계
① 특정 cell type이 어디에 위치하는지 알기 어려움
○ 이유 1. spatial transcriptomics spots 위에 single-cell이 놓이지 않고 수십~수백 개의 cell들이 놓일 수 있기 때문
○ 이유 2. spot 위에 수 개의 cell들만 올라가더라도 별개의 cell로 인식하지 못하고 하나의 새로운 cell로 인식함
② 기존 unsupervised marker-dependent analysis의 단점 (ref)
○ 단점 1. 통계적으로 platform effect, Poisson sampling, over-dispersed counts 등의 문제를 제어하지 못함
○ 단점 2. 실제로 performance가 그렇게 뛰어나지 않음
③ 기존 MIA 분석(multimodal intersection analysis)의 단점 (ref)
○ 단점 1. 통계적으로 platform effect, Poisson sampling, over-dispersed counts 등의 문제를 제어하지 못함
○ 단점 2. Slide-seq와 같은 large-scale spatial transcriptomics에서 검증되지 않았음
○ 단점 3. 파라미터 조절이 어려워 enhancement나 depletion로 치우치기 쉬움
○ 단점 4. 파라미터에 따라 결과가 예민하게 변함
○ (주석) 단점 1과 단점 2는 논문에서 지적한 사항이고 단점 3과 단점 4는 실무자로서의 필자의 입장을 적은 것
⑵ RCTD(robust cell type decomposition)
① 특징 : spatial transcriptomics data에서 특정 cell type을 구분할 수 있음. supervised
② 의의 1. 다른 supervised method와 달리 특정 spot 상에서 multiple cell type의 구분이 가능함
③ 의의 2. platform effect를 제어할 수 있음 : supervised method에서 platform effect가 제어되지 않으면 technical variability가 biological signal을 앞도하여 성공적인 분석이 되기 어려움
2. 수학적 이론 [목차]
⑴ statiscal model

① 기본적으로 푸아송 모델(Poisson model)을 따름
○ Slide-seq과 같이 UMI count가 낮은 경우에도 사용할 수 있음
② i : 각 스팟. 1, ..., I
③ j : 각 유전자. 1, ..., J
④ k : 각 cell type. 1, ..., K
⑤ Yi,j : i번째 스팟에서 j번째 유전자의 gene expression (단위 : count)
⑥ λi,j : platform effect, 기타 natural variability를 반영하는 랜덤 확률변수 (단위 : 없음)
⑦ Ni: 각 스팟의 total transcript count. 이를 UMI(unique molecular identifier)라고 함
⑧ αi : i번째 스팟에 특이적인 고정 효과
⑨ γj : j번째 유전자에 특이적인 고정 효과
○ scRNA-seq, snRNA-seq, Slide-seq, Smart-seq 등 platform-specific
○ 평균이 0이고 표준편차가 σγ인 정규분포를 따른다고 가정
⑩ μk,j : k번째 cell type에서 j번째 유전자의 평균 유전자 발현 (단위 : normalized expression)
⑪ βi,k : i번째 스팟에서 k번째 cell type에 대한 가중치
○ 조건 1. βi,k + ··· + βi,K = 1
○ 조건 2. βi,k ≥ 0
○ β값들을 알아내면 모델을 완성할 수 있음
⑫ εi,j : i번째 스팟에서 j번째 유전자 발현에 영향을 주는 랜덤 효과. gene-specific overdispersion 관련
○ 평균이 0이고 표준편차가 σε인 정규분포를 따른다고 가정
⑵ supervised learning
① Step 1. 레퍼런스로부터 μk,j를 구한 뒤 spatial transcriptomics에서도 이 값은 동일할 것이라고 가정
○ 레퍼런스에서 k번째 cell type의 모든 single cell들의 유전자 j의 expression의 평균
② Step 2. cell type 간에 유의미한 차이를 보이지 않는 유전자들은 제외 (∵ 데이터 분석의 성능을 높이기 위함)
○ 30,000개의 유전자 중 대략 5,000개의 유전자만 남게 됨
③ Step 3. 다음 수식을 전개하면 신기하게도 γj를 결정할 수 있음

○ Sub-step 1. Sj ≡ ∑(i = 1 to I) Yi,j
○ Sub-step 2. (첫 번째 등호) Y ~ Possion(λ)에 대하여 E(Y) = λ임을 이용 (푸아송 분포)
○ Yi,j의 i에 대한 표본평균의 합 또한 푸아송 분포를 따름 : 다음은 이를 증명하는 과정임
○ 적률생성함수의 성질 : ψX1+X2(t) = ψX1(t) × ψX2(t)
○ 가정 : X1 ~ Poisson(λ1), X2 ~ Poisson(λ2)
○ ψX1(t) = exp(λ1et - λ1), ψX2(t) = exp(λ2et - λ2)
○ ΨX1+X2(t) = exp((λ1+λ2)et - (λ1+λ2))
○ 결론 : X1 + X2 ~ Poisson(λ1 + λ2)
○ Sub-step 3. (두 번째 등호)
○ 3-1. λi,j를 대입
○ 3-2. γj 항을 분리 : i와 무관한 항이므로 쉽게 분리할 수 있음
○ 3-3. ∑ (i = 1 to I)와 ∑ (k = 1 to K)의 순서를 바꿈
○ Sub-step 4. I가 충분히 크면 Var(Bk,j)는 0으로 수렴하기 때문에 (supplementary method) Bk,j ≒ βk
○ Sub-step 5. Sj에 대한 최대우도추정(maximum likelihood estimation)을 통해 β0, βk, σγ의 점추정량을 구할 수 있음
○ Sub-step 6. σγ를 가지고 랜덤하게 γj를 할당
④ Step 4. (RCTD)
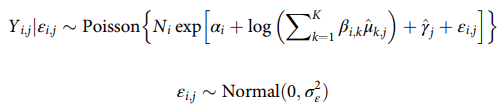
○ 특정 spot 상에서 유전자 j를 달리하면서 Yi,j에 대한 최대우도추정을 통해 αi, βi,k, σε에 대한 점추정량을 구할 수 있음
⑶ optimized supervise learning
① spot마다 최대 겹치는 cell type이 2개라고 가정 : 즉, spot은 singlet이거나 doublet
② 물론, spot 별 cell type의 개수의 최댓값을 제한하거나 아예 제한 자체를 안 할 수 있음
③ optimization을 하면 overfitting을 예방할 수 있음 : singlet은 cell type 개수가 spot별로 1개이므로 doublet이 바람직함
3. 코드 : R을 통해 구현 [목차]
⑴ R의 설치
⑵ https://github.com/dmcable/RCTD
GitHub - dmcable/RCTD
Contribute to dmcable/RCTD development by creating an account on GitHub.
github.com
⑶ https://raw.githack.com/dmcable/RCTD/dev/vignettes/spatial-transcriptomics.html
Applying RCTD to Spatial Transcriptomics Data
library(RCTD) library(Matrix) Introduction Robust Cell Type Decomposition, or RCTD, is an R package for learning cell types from spatial transcriptomics data. In this Vignette, we will assign cell types to a cerebellum Slide-seq dataset. We will define cel
raw.githack.com
⑷ 필요한 파일

Figure. 1. meta_data.csv

Figure. 2. BeadLocationsForR.csv

Figure. 3. MappedDGEForR.csv
4. 결과 [목차]
⑴ challenge
① 기존 unsupervised marker-dependent analysis의 단점 재확인
○ 단점 1. Bergmann cell과 Purkinje cell처럼 colocalize하는 경우 marker gene의 구분이 뚜렷하지 않음 : unsupervised learning은 colocalize하는 경우 아예 이 둘을 합한 새로운 cell type으로 인식하기 때문 (Fig. 1a)
○ 단점 2. 실제로 granule cell을 분류할 때 잘못 분류함 (Fig. 1b, c)
② 기존 supervised analysis의 단점 재확인
○ 단점 : cross-platform cell type classification 퍼포먼스가 그렇게 훌륭하지 않음 (Fig. 1d, e)
③ RCTD는 이러한 문제점들을 해결할 수 있음
○ RCTD는 platform-effect를 효과적으로 제거할 수 있음 (Fig. 2b)
○ RCTD는 high cross-platform single-cell classification accuracy를 보임 (Fig. 2c)
○ RCTD는 Bergmann, Purkinje doublet 상황에서도 Bergmann을 잘 포착함 (Fig. 3c)
○ 만일 레퍼런스에 해당하는 cell type이 없다면 대개 잘못된 cell로 분류함 (supplementary Fig. 11)
⑵ mouse cerebellum 샘플
① mouse cerebellum의 구조

Figure. 4. mouse cerebellum의 구조
② snRNA-seq reference × Slide-seqV2
○ 결과적으로 나오는 cell type이 cerebellum의 spatial architecture을 잘 반영함 (Fig. 4a)
○ RCTD을 singlet, doublet mode로 설정한 결과 Purkinje cell과 Bergmann cell을 예상대로 구분해 냄 (Fig. 4b, 4c)
○ 실제 marker와 비교해 본 결과 correspondence가 훌륭함 (Fig. 4d)
③ scRNA-seq reference × Slide-seqV2
○ snRNA-seq reference × Slide-seqV2에서 한 cell type prediction과 95.7%가 일치함
○ 이 밖에도 다양한 분석이 RCTD의 consistency를 보여줌
⑶ 해마(hippocampus) 샘플
① RCTD-based interneuron cell type와 interneuron marker의 co-localization (Fig. 5b)
② RCTD-based interneuron marker 내에서의 sub-cluster와 Sst expression의 co-localization (Fig. 5c, 5d)
③ RCTD는 유전자 발현에 있어 cellular environment의 영향을 보여줄 수 있음 (Fig. 6g)
5. 결론 [목차]
⑴ 한계 1. platform effect가 모든 cell type에 공통된다는 가정을 함 : cell-type-specific platform effect를 조사해야 할 듯
⑵ 한계 2. spatial data에는 있지만 reference에서는 누락된 cell type이 문제가 될 수 있음
⑶ 의문 : μk,j의 단위가 normalized expression인지 이해가 안 됨
⑷ 응용 : spatial transcriptomic × spatial transcriptomic와 같은 식으로도 진행할 수 있을 듯
입력: 2021.06.04 00:34
'▶ 자연과학 > ▷ 생물정보학' 카테고리의 다른 글
| 【생물정보학】 유전자 라이브러리 (0) | 2022.06.02 |
|---|---|
| 【생물정보학】 xFuse의 이해 및 실행 (0) | 2022.01.11 |
| 【생물정보학】 CellPhoneDB의 이해 (0) | 2021.04.13 |
| 【생물정보학】 데이터 분석 : Kaplan-Meier 생존 곡선 (0) | 2021.04.13 |
| 【생물정보학】 MIA 분석의 이해 및 실행 (0) | 2021.01.02 |



최근댓글