【빅데이터분석기사】 R 실기 필수 암기 및 예제

R 실기 필수 암기 및 예제

추천글 : 【빅데이터분석기사】 빅데이터분석기사 목차

a. R에서 유용한 주요 함수 모음

b. 파이썬 실기 필수 암기 및 예제

※ 필자는 불필요하게 암기 부담을 늘리는 것보다 몇몇 필수 암기 사항을 토대로 응용하는 게 중요하다고 생각합니다.

※ 코드 - 설명 순으로 정리해 두었습니다. 쉬운 순서부터 나열하였습니다.

※ 제6회 빅데이터분석기사 실기시험(2023.06.24)부터 기존 단답형 10문제를 작업형 신규 유형인 '작업형 제3유형'으로 대체 (ref)

※ 일반적으로 유형 1은 파이썬으로 풀기 좋고, 유형 2, 유형 3은 R로 풀기를 권장합니다.

※ 빅데이터분석기사 실기 체험 : 실행시간만 1분으로 한계가 있고, 실행횟수는 제한 없음

# "#"은 주석 표시를 의미함
# x <- 1과 x = 1은 완전히 동일함
# setwd(), getwd() 등 작업 폴더 설정 불필요
# 파일 경로 상 내부 드라이브 경로(C: 등) 접근 불가
예제 데이터
mtcars
iris
data(wine, package = "rattle")
data("Titanic")
data(Diabetes, package="heplots")
data("tips", package = "reshape2")
x = c(1, 2, 3, 4) : 벡터 데이터 선언
변수 확인
typeof(x) : x의 자료형을 출력
is.na(x) : x가 NA인지 여부
is.numeric(x) : x가 숫자형 데이터인지
array() : 배열 선언
matrix() : 행렬 선언
x = as.numeric(x) : x를 숫자형 변수로 바꾸기
x = as.vector(x) : x를 벡터형 변수로 바꾸기
x = as.data.frame(x) : x를 데이터프레임으로 바꾸기
x = as.matrix(x) : x를 행렬로 바꾸기
x = as.factor(x) : x를 명목변수로 만들기
rownames(x) : 행렬 혹은 데이터프레임 변수인 x의 행 이름
colnames(x) : 행렬 혹은 데이터프레임 변수인 x의 열 이름
names(x) : 데이터프레임 변수인 x의 열 이름
slotName(x) : x라는 R 객체 내 슬롯명을 보기
head(x) : x의 초기 데이터 확인 (▶️ 파이썬에서는 df.head())
tail(x) : x의 후기 데이터 확인 (▶️ 파이썬에서는 df.tail())
length(x) : x라는 벡터 데이터의 길이를 표시
dim(x) : x라는 행렬 혹은 데이터프레임 데이터의 행, 열 확인 (▶️ 파이썬에서는 df.shape)
sum(is.na(df)) : 데이터프레임 df에서 결측치의 개수의 합 (▶️ 파이썬에서는 df.isnull().sum())
df = na.omit(df) : 데이터프레임 df에서 결측치 제거 (▶️ 파이썬에서는 df.dropna())
df[is.na(df)] <- 0 : 데이터프레임 df에서 결측치를 0으로 치환
df = df[, -c("v1", "v2")] : 데이터프레임 df에서 불필요한 칼럼들 제거 (▶️ 파이썬에서는 df = df.drop(cloumns = ['v1', 'v2']))
x = rbind(df1, df2) : 두 데이터프레임의 열이 공통일 때, 행 방향으로 합치기
x = cbind(df1, df2) : 두 데이터프레임의 행이 공통일 때, 열 방향으로 합치기
x = read.csv("FILE_NAME.csv") : CSV 파일 읽기
x = read.table("FILE_NAME.txt") : txt 파일 읽기
x = read.xlsx("FILE_NAME.xlsx") : xlsx 엑셀 파일 읽기
x = read.delim("FILE_NAME") : 아무 파일 읽기
write.csv(x, "FILE_NAME.csv") : CSV 파일 쓰기
attach(df) : 데이터프레임 df의 column 이름을 별도의 변수처럼 호출할 수 있게 함
for (x in 1:10) : for 문
if(x == 1) : if 문
x = mtcars[order(mtcars$mpg, decreasing=TRUE), ] : mtcars의 mpg 값을 내림차순으로 하여 재정렬
match(e, x) : x라는 벡터 데이터에서 e라는 원소가 몇 번째에 있는지
grepl(partial_str, given_str, fixed = TRUE) : 주어진 문자열(given_str)에서 특정 문자열(partial_str)을 포함하는지 여부
x %in% arr : x 혹은 x의 각 원소가 arr에 속하는지 여부
통계 처리
abs(x) : x의 절댓값
sqrt(x) : x의 양의 제곱근
log(x) : x의 자연로그 변환
mean(x) : 벡터형 변수인 x의 평균값
median(x) : 벡터형 변수인 x의 중위수
sd(x) : 벡터형 변수인 x의 표준편차
cor(x, y) : 피어슨 상관계수
cor(x, y, method = "pearson") : 피어슨 상관계수
cor(x, y, method = "spearman") : 스피어만 상관계수
cor(x, y, method = "kendall") : 켄달 상관계수
round(x, n) : x를 소수점 이하 n 자리까지만 남기고 반올림하는 것
signif(x, n) : x에서 유효숫자를 n개만 남기도 반올림하는 것
summary(x) : 벡터, 데이터 프레임, 혹은 모델 변수인 x의 요약 정보
quantile(x, p) : x라는 벡터 데이터를 p% 분위수 값을 출력
unique(x) : x라는 벡터 데이터의 고유한 값들만 출력
table(x) : x라는 벡터 데이터의 각 원소별 빈도를 출력. 일종의 'groupby'
gsub("-", "", str) : 주어진 문자열에서 하이픈(-)을 제거하는 함수
분산분석
shapiro.test(x) : 벡터형 변수 x가 정규성을 따르는지에 대한 검정
bartelett(x, y) : 등분산성 검정 (표본이 정규분포를 따르는 경우)
leveneTest(response ~ group, data = data) : 등분산성 검정 (표본이 정규분포를 따르지 않거나 표본이 작은 경우)
t.test(x, mu = y) : 정규분포를 따르는 벡터형 변수 x가 y와 같다고 할 수 있는지에 대한 검정. 단측검정 시, 여기에서 얻은 p value 값의 반이 됨
wilcox.test(x, mu = mean) : 정규분포를 따르지 않는 벡터형 변수 x가 y와 같다고 할 수 있는지에 대한 검정
t.test(x, y, paired = TRUE) : 두 벡터형 변수 x, y의 t test (대응표본 모수 검정)
t.test(x, y, paired = FALSE) : 두 벡터형 변수 x, y의 t test (독립표본 모수 검정)
wilcox.test(x, y, paired = TRUE) : 윌콕슨 부호순위검정 (대응표본 비모수 검정)
wilcox.test(x, y, paired = FALSE) : 윌콕슨 순위합 검정 (독립표본 비모수 검정)
chisq.test(x, y) : 두 벡터형 변수 x, y의 카이제곱검정
aov(y ~ x, data = my_data) : ANOVA 분석 (분산분석 모수 검정)
kruskal.test(y ~ x, data = my_data) : 크루스칼-월리스 검정 (분산분석 비모수 검정)
회귀분석
lm(y ~ x1 + x2, data = my_data) : 선형회귀분석
glm(y ~ x1 + x2, data = my_data, family = binomial) : 로지스틱 회귀
glm(y ~ x1 + x2, data = my_data, family = binomial(link = "logit")) : 로지스틱 회귀. Pr = 1 / ( 1 + exp(-(βx + β₀)) )와 같은 식
glm(y ~ x1 + x2, data = my_data, family = binomial(link = "probit")) : probit 회귀. Pr = Φ(βx + β₀) = Φ(Z)

A. 제1유형 (30점; 3문제)

○ 데이터 타입 : object, int, float, bool 등

○ 기초 통계량 : 평균, 중앙값, 사분위수, IQR, 표준편차 등

○ 데이터 인덱싱, 필터링, 정렬, 변경 등

○ 결측치, 이상치, 중복값 처리 (제가 또는 대체)

○ 데이터 정규화 : Z-scaling, min-max normalization 등

○ 데이터 합치기

○ 날짜/시간 데이터

예시 1.

제공된 데이터(data/mtcars.csv)의 qsec 칼럼을 최소-최대 척도(Min-Max Scale)로 변환한 후 0.5보다 큰 값을 가지는 레코드 수를 【제출 형식】에 맞게 답안 작성 페이지에 입력하시오.

【유형 1】

㉠ 정수(integer)로 입력 (단, 소수점을 포함한 경우 소수점 첫째 자리에서 반올림하여 계산)

㉡ 정수 답안만 입력

풀이.

a <- read.csv("./data/mtcars.csv")
a = na.omit(a)
vmax = max(a$qsec)
vmin = min(a$qsec)
a$qsec = (a$qsec - vmin)/(vmax - vmin)
v = sum(a$qsec > 0.5)
v = round(v, 0)
print(v)

B. 제2유형 (40점; 1문제)

전략

○ 분류모델 : 연속 변수로 명목 변수를 예측. SVM, 결정나무, 랜덤 포레스트(분류 알고리즘 중 가장 뛰어남)를 주로 사용

○ 회귀모델 : 연속 변수로 연속 변수를 예측. 선형회귀, probit, logit을 주로 사용

○ 대체로, 문제 풀이는 다음과 같은 순서로 풀이 (단, 다음은 pseudo-code임을 유의)

X_train['y_train'] = y_train
model = func(y ~ x1, ..., xn, data = X_train, mode = ...)
pred = predict(model, X_test)

예시 1.

제공된 데이터는 백화점 고객이 1년간 상품을 구매한 속성 데이터이다. 제공된 학습용 데이터(data/customer_train.csv)를 이용하여 백화점 구매 고객의 성별을 예측하는 모델을 개발하고, 개발한 모델에 기반하여 평가용 데이터(data/customer_test.csv)에 적용하여 얻은 성별 예측 결과를 【제출 형식】에 따라 CSV 파일로 생성하여 제출하시오.

* 예측 결과는 ROC-AUC 평가지표에 따라 평가함

* 성능이 우수한 예측 모델을 구축하기 위해서는 데이터 정제, Feature Engineering, 하이퍼 파라미터(hyper parameter) 최적화, 모델 비교 등이 필요할 수 있음. 다만, 과적합에 유의하여야 함.

【제출 형식】

㉠ CSV 파일명 : result.csv (파일명에 디렉토리∙폴더 지정 불가)

㉡ 예측 성별 칼럼명 : pred

㉢ 제출 칼럼 개수 : pred 칼럼 1개

㉣ 평가용 데이터 개수와 예측 결과 데이터 개수 일치 : 2,482개

풀이 1. probit regression : 정확하지 않으므로 선호하지 않음

train = read.csv("./data/customer_train.csv")
test = read.csv("./data/customer_test.csv")
train = na.omit(train)
test = na.omit(test)

train$성별 = as.factor(train$성별)
model = glm(성별 ~ 총구매액 + 최대구매액 + 환불금액 + 방문일수 + 방문당구매건수 + 주말방문비율 + 구매주기,
					 data = train, family=binomial(link = 'probit'))
probabilities = predict(model, test)
pred = array()
for(i in 1:dim(test)[1]){
	pred[i] = as.numeric(probabilities[i] > 0.5)
}
pred = as.data.frame(pred) # to properly save a csv file

write.csv(pred, "result.csv", row.names = FALSE)
result = read.csv("result.csv")
print(result)

풀이 2. SVM

library(e1071)

train = read.csv("./data/customer_train.csv")
test = read.csv("./data/customer_test.csv")
train = na.omit(train)
test = na.omit(test)

train$성별 = as.factor(train$성별)
sv = svm(성별 ~ 총구매액 + 최대구매액 + 환불금액 + 방문일수 + 방문당구매건수 + 주말방문비율 + 구매주기,
					 data = train)
pred = predict(sv, test)
pred = as.data.frame(pred) # to properly save a csv file

write.csv(pred, "result.csv", row.names = FALSE)
result = read.csv("result.csv")
print(result)

풀이 3. 랜덤 포레스트 : SVM과 달리, 각 클래스별 확률을 계산할 수도 있음

library(randomForest)

train = read.csv("./data/customer_train.csv")
test = read.csv("./data/customer_test.csv")
train = na.omit(train)
test = na.omit(test)

train$성별 = as.factor(train$성별)
model = randomForest(성별 ~ 총구매액 + 최대구매액 + 환불금액 + 방문일수 + 방문당구매건수 + 주말방문비율 + 구매주기,
					 data = train)
pred = predict(model, test)
pred = as.data.frame(pred) # to properly save a csv file

write.csv(pred, "result.csv", row.names = FALSE)
result = read.csv("result.csv")
print(result)

예시 2. (정식 문제는 아님)

다음과 같은 예제 데이터가 주어져 있을 때, x_train, y_train으로부터 모델을 생성하여 x_test로부터 y_test를 예측하여라.

# Load required libraries
library(dplyr)
library(caret)

# Load the wine dataset
data(wine, package = "rattle")
wine_data <- wine

# Create a data frame for features (x) and target (y)
x <- wine_data %>% select(-Type)  # Select all columns except 'Type' which is the target
y <- wine_data %>% select(Type)   # Select only the 'Type' column

# Split the dataset into training and test sets
set.seed(123)  # For reproducibility
trainIndex <- createDataPartition(y$Type, p = 0.8, list = FALSE)
x_train <- x[trainIndex, ]
y_train <- y[trainIndex, ]
x_test <- x[-trainIndex, ]
y_test <- y[-trainIndex, ]

# Additional manipulations as per the Python code
x_test <- as.data.frame(x_test)
x_train <- as.data.frame(x_train)
y_train <- as.data.frame(y_train)

# Reset index in x_test (not typically done in R, but for parity with Python code)
x_test <- x_test %>% mutate(index = row_number()) %>% select(index, everything())

# Rename the column in y_train
names(y_train)[1] <- 'target'

풀이 1. SVM

library(e1071)

x_train['target'] = y_train[,1]
x_train$target = as.factor(x_train$target) # necessary
sv <- svm(target ~ ., data = x_train)
pred = predict(sv, x_test) 

print(sum(y_test == pred) / length(y_test)) # accuracy

풀이 2. 랜덤 포레스트 : SVM과 달리, 각 클래스별 확률을 계산할 수도 있음

library(randomForest)

x_train['target'] = y_train[,1]
x_train$target = as.factor(x_train$target) # necessary

model <- randomForest(target ~ ., data = x_train)
pred = predict(model, x_test)
print(sum(y_test == pred) / length(y_test)) # accuracy

prob_estimates <- predict(model, x_test, type = "prob") # SVM은 원리상 이 기능이 작동하지 않음

예시 3. (정식 문제는 아님)

다음과 같은 예제 데이터가 주어져 있을 때, x_train, y_train으로부터 모델을 생성하여 x_test로부터 y_test를 예측하여라.

# Load required libraries
library(dplyr)
library(caret)

# Load the iris dataset (included in base R)
data(iris)

# Rename the columns for consistency with the Python code
names(iris) <- c('sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species')

# Convert species to a binary factor: 'setosa' as 0 and others as 1
iris$species <- as.numeric(iris$species != 'setosa')

# Split the data into training and testing sets
set.seed(123)  # for reproducibility
trainIndex <- createDataPartition(iris$species, p = 0.8, list = FALSE)
trainData <- iris[trainIndex, ]
testData <- iris[-trainIndex, ]

# Convert first entry of sepal_length to NA (missing value)
trainData$sepal_length[1] <- NA
testData$sepal_length[1] <- NA

# Insert an outlier in sepal_width
trainData$sepal_width[1] <- 150

# Wrap-up
trainData = na.omit(trainData)
x_train = trainData[, 1:4]
y_train = trainData[5]
testData = na.omit(testData)
x_test = testData[, 1:4]
y_test = testData[, 5]

풀이 1. SVM

library(e1071)

x_train['species'] = y_train[,1]
x_train$species = as.factor(x_train$species) # necessary
sv <- svm(species ~ ., data = x_train)

pred = predict(sv, x_test)

print(sum(y_test == pred) / length(y_test)) # accuracy

풀이 2. 랜덤 포레스트 : SVM과 달리, 각 클래스별 확률을 계산할 수도 잇음

library(randomForest)

x_train['species'] = y_train[,1]
x_train$species = as.factor(x_train$species) # necessary

model <- randomForest(species ~ ., data = x_train)
pred = predict(model, x_test)
print(sum(y_test == pred) / length(y_test)) # accuracy

prob_estimates <- predict(model, x_test, type = "prob") # SVM은 원리상 이 기능이 작동하지 않음
prob_estimates

예시 4. (정식 문제는 아님)

다음과 같은 예제 데이터가 주어져 있을 때, x_train, y_train으로부터 모델을 생성하여 x_test로부터 y_test를 예측하여라.

# Load required libraries
library(tidyverse)
library(caret)

# Load the Titanic dataset from a package or a source that you have
# Note: Ensure that the dataset structure matches with what you expect
# For this example, I'm using the Titanic dataset from the datasets package
data("Titanic")
df <- as_tibble(Titanic)

# Selecting columns and target variable
# Adjust the column names according to your dataset
x <- select(df, -Survived) 
y <- df$Survived

# Split the data into training and test sets
set.seed(123) # for reproducibility
trainIndex <- createDataPartition(y, p = .8, list = FALSE, times = 1)
x_train <- x[trainIndex, ]
y_train <- y[trainIndex]
x_test  <- x[-trainIndex, ]
y_test  <- y[-trainIndex]

# Convert y_train and y_test to tibble with a new column name
y_train <- tibble(target = y_train)
y_train = as.data.frame(y_train)
y_test <- tibble(target = y_test)
y_test = as.data.frame(y_test)

# Convert x_train and x_test to tibble (optional if they are already tibbles)
x_train <- as_tibble(x_train)
x_train = as.data.frame(x_train)
x_test <- as_tibble(x_test)
x_test = as.data.frame(x_test)

풀이 1. SVM

library(e1071)

x_train['target'] = y_train
x_train$target = as.factor(x_train$target) # necessary

sv <- svm(target ~ ., data = x_train)
pred = predict(sv, x_test)
print(sum(y_test$target == pred) / length(y_test$target)) # accuracy

풀이 2. 랜덤 포레스트 : SVM과 달리, 각 클래스별 확률을 계산할 수도 있음

library(randomForest)

x_train['target'] = y_train
x_train$target = as.factor(x_train$target) # necessary

model <- randomForest(target ~ ., data = x_train)
pred = predict(model, x_test)
print(sum(y_test$target == pred) / length(y_test$target)) # accuracy
 
prob_estimates <- predict(model, x_test, type = "prob") # SVM은 원리상 이 기능이 작동하지 않음
prob_estimates

C. 제3유형 (30점; 2문제; 문제마다 소문제 존재)

전략

필자의 경우 새로운 함수를 많이 익히지는 않는 방향으로 문제를 풀려고 함

예시 1.

제공된 데이터(data/Titanic.csv)는 타이타닉호의 침몰 사건에서 생존한 승객 및 사망한 승객의 정보를 포함한 자료이다. 아래 데이터를 이용하여 생존 여부(Survived)를 예측하고자 한다. 각 문항의 답을 【제출 형식】에 맞춰 답안 작성 페이지에 입력하시오. (단, 벌점화(penalty)는 부여하지 않는다.)

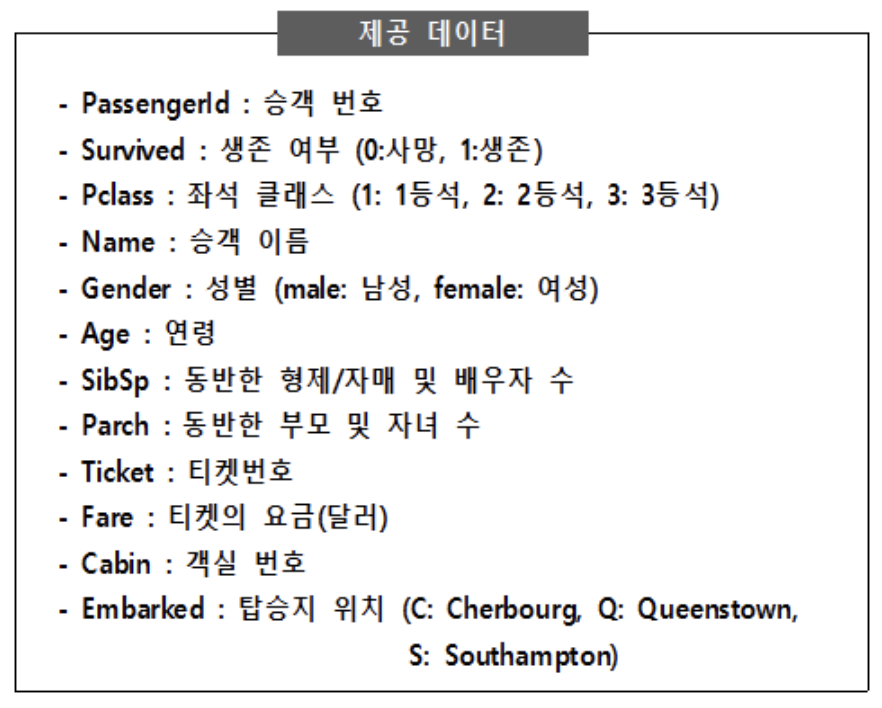
① Gender와 Survived 변수 간의 독립성 검정을 실시하였을 때, 카이제곱 통계량은? (반올림하여 소수 셋째 자리까지 계산)

② Gender, SibSp, Parch, Fare를 독립변수로 사용하여 로지스틱 회귀모형을 실시하였을 때, Parch 변수의 계수값은? (반올림하여 소수 셋째 자리까지 계산)

③ 위 ②번 문제에서 추정된 로지스틱 회귀모형에서 SibSp 변수가 한 단위 증가할 때 생존할 오즈비(Odds ratio) 값은? (반올림하여 소수 셋째 자리까지 계산)

【제출 형식】

㉠ 소수 넷째 자리에서 반올림하여 소수 셋째 자리까지만 계산

풀이.

① 카이제곱검정 테스트 : 답은 260.717

a <- read.csv("data/Titanic.csv")

library(dplyr)

result_chisq <- chisq.test(a$Gender, a$Survived)

print(round(result_chisq$statistic,3))

②, ③ 로지스틱 회귀 : 답은 각각 -0.201, 0.702

a <- read.csv("data/Titanic.csv")

# a = na.omit(a) : 관련 없는 칼럼에서 생긴 결측치를 가지고 튜플을 제외하면 최종답이 달라짐 

md_glm <- glm(Survived ~ Gender + SibSp + Parch + Fare, data=a, family=binomial(link="logit"))

val = as.numeric(md_glm[[1]][4])

print(round(val, 3))

val2 = as.numeric(md_glm[[1]][3])

print(round(exp(val2), 3))

입력: 2023.11.19 18:45

수정: 2023.11.22 13:10

저작자표시

'▶ 자연과학 > ▷ 컴퓨터과학' 카테고리의 다른 글

【빅데이터분석기사】 파이썬 실기 필수 암기 및 예제 (1)	2024.06.02
【빅데이터분석기사】 필기 키워드 정리 (0)	2023.11.19
【Excel】 Excel 단축키 모음 (0)	2021.09.09
【컴퓨터 활용】 Excel 목차 (0)	2018.10.05
【한글】 자주 쓰는 한글 단축키 (0)	2018.10.03

정빈이의 공부방

최근댓글

【빅데이터분석기사】 R 실기 필수 암기 및 예제

'▶ 자연과학 > ▷ 컴퓨터과학' 카테고리의 다른 글

티스토리툴바

【빅데이터분석기사】 R 실기 필수 암기 및 예제

'▶ 자연과학 > ▷ 컴퓨터과학' 카테고리의 다른 글

'▶ 자연과학/▷ 컴퓨터과학' 관련 포스팅

티스토리툴바